ホームページ >バックエンド開発 >Python チュートリアル >Pythonソートアルゴリズムの選択ソートを実装する方法
Pythonソートアルゴリズムの選択ソートを実装する方法
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB転載
- 2023-05-17 21:23:371103ブラウズ
1. はじめに
プライマリ ソート アルゴリズムとは、比較的基本的で理解しやすいいくつかのソート アルゴリズムを指します。主なソート アルゴリズムには、挿入ソート、選択ソート、バブル ソートの 3 つがあります。効率は高度な並べ替えアルゴリズムよりも劣りますが、基本的な並べ替えアルゴリズムを理解した後は、比較的複雑な高度な並べ替えアルゴリズムを学習するのがはるかに簡単になります。
2. 説明
選択ソートとは、順序なし配列から毎回最小または最大のデータを選択し、それを順序なし配列から順序付き配列の最後に配置して並べ替え効果を実現することを意味します。
選択ソートの平均時間計算量は O(n2) で、最良の場合の時間計算量と最悪の場合の時間計算量は両方とも O(n2) です。さらに、これは不安定な並べ替えアルゴリズムです。選択ソートプロセスは理解しやすいです。昇順ソート アルゴリズムを例にとると、図 2-4 に示すように、まず未ソートの配列を走査して最小の要素を見つけます。次に、ソートされていない配列から最小の要素を削除し、ソートされた配列の末尾に追加します。
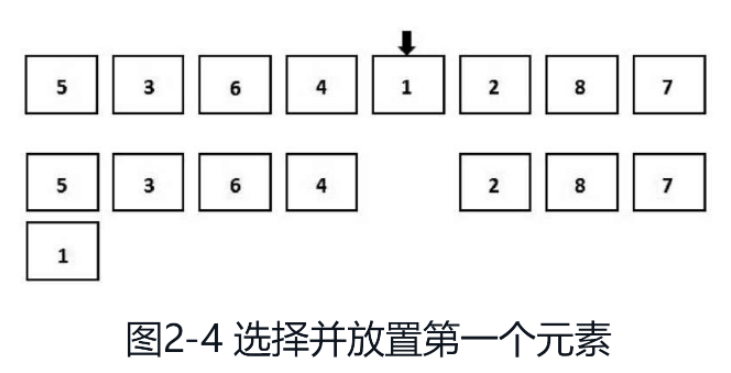
最小の要素は 1 であるため、まだ空である順序付けされた配列の最後に 1 が追加されます。
図 2-5 に示すように、残りの要素のトラバースを続けます。今回の最小要素は2です。これをソートされた配列の末尾に追加します。ソートされた配列の要素はソートされていない配列の要素よりも小さい必要があるため、この操作は正しいです。
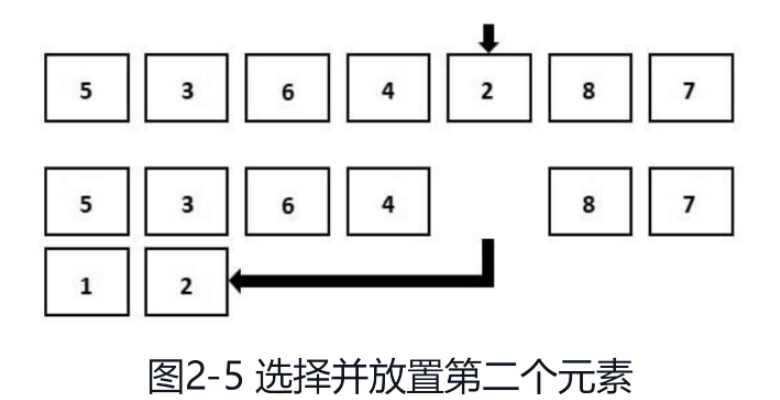
図 2-6 に示すように、上記の手順を繰り返し、並べ替えられていない配列に要素が 1 つだけ残ったら、それを並べ替えた配列の末尾に追加します。全体 配列のソートが完了しました。
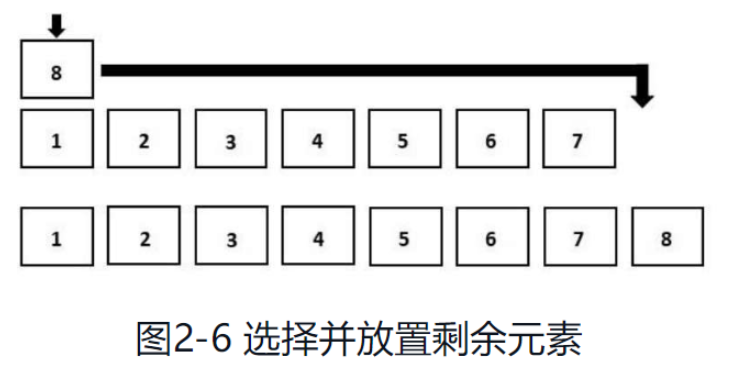
3. コードの実装
ソート コードを選択します:
nums = [5,3,6,4,1,2,8,7]
res = [] #用于存储已排序元素的数组
while len(nums): #当未排序数组内还有元素时,重复执行选择最小数的代码
minInd = 0 #初始化存储最小数下标的变量,默认为第一个数
for i in range(1, len(nums)):
if(nums[i] < nums[minInd]): #更新最小数的下标
minInd = i
temp = nums[minInd]
nums.pop(minInd) #把最小数从未排序数组中删除
res.append(temp) #把最小数插入到已排序数组的末尾
print(res)プログラムを実行すると、出力結果は次のようになります:
[1,2,3,4,5,6,7,8]
プログラムでは、最初の for ループの i は、ソートされていない配列の最初の位置、つまり、順序付けされた配列の後の最初の位置を表します。次に、for ループを使用して、ソートされていない配列内の最小値の添え字を見つけます。最初に、最小インデックス minInd に、ソートされていない配列の最初の要素のインデックスが割り当てられます。現在の最小値より小さい要素が見つかった場合は、インデックスを更新し、配列全体を反復処理します。見つかった最小値をソートされていない配列の最初の要素と交換した後、最小値が順序付けされた配列の最後に配置されます。
以上がPythonソートアルゴリズムの選択ソートを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

