3 次元の世界に住む人々として、私たちは皆、次のような疑問を考えたことがあるでしょう。タイムトラベルは可能でしょうか?
1916 年、オーストリアの物理学者ルートヴィヒ フラムが最初に「ワームホール」の概念を提案しました。1930 年代には、アインシュタインとネイサン ローゼンが重力場の研究をしていました。この方程式は、ブラック ホールとホワイトホールはワームホールを介してつながっているため、「ワームホール」は「アインシュタイン・ローゼン橋」とも呼ばれます。 「ワームホール」は、物体が時間と空間を瞬時に移動できる宇宙の「ショートカット」の可能性があると考えられています。しかし、科学者たちはワームホールの客観的な存在を確認できていません。
さて、科学者たちが史上初のワームホールを作成し、その研究論文がネイチャー誌の表紙を飾りました。

論文アドレス: https://www.nature.com/articles/s41586-022-05424-3
ワームホールはホログラムのようなもので、小さな超伝導回路に保存された情報の量子ビット、つまり「量子ビット」で構成されています。この研究では、量子ビットを操作することでワームホールを通じて情報を送信することに成功した。
この研究は、カリフォルニア工科大学の物理学教授マリア スピロプル氏が主導し、研究チームは Google の量子コンピューター Sycamore を使用して、新しい「ワームホール テレポーテーション プロトコル」を実装しました。
 カリフォルニア工科大学の物理学者、マリア・スピロプル。出典: クォンタムマガジン。
カリフォルニア工科大学の物理学者、マリア・スピロプル。出典: クォンタムマガジン。
ホログラフィック原理は、ブラック ホールの量子特性に基づいた基本原理であり、基礎物理学、量子力学、一般相対性理論が関係します。物理学者は 1930 年代以来、これらの異なる理論を調和させようと試みてきました。 1990 年代以来、ホログラフィック原理は、2 つの枠組み間の数学的等価性または「二重性」を提案してきました。ホログラフィック原理では、一般相対性理論によって記述される湾曲した時空連続体は、実際には変装した粒子の量子システムであると考えられます。 3D ホログラムが 2D パターンから投影されるのと同じように、時空と重力は量子効果から生じます。
スピロプルらによって行われた新しい実験は、量子コンピューターで量子効果を制御し、相対性理論で期待される現象であるワームホールを生成できることを確認しました。
はっきり言っておきますが、通常のホログラムとは異なり、ワームホールは目に見えるものではありません。ワームホールの主任開発者でハーバード大学の共著者であるダニエル・ジャフェリス氏は、私たちの研究結果は「現実の時空フィラメント」伝送プロトコルとみなすことができるが、それは私たちと同じ現実世界の一部ではないと信じています。シカモアコンピューターが生息しています。ホログラフィック原理は、これら 2 つの現実 (ワームホールのあるものと量子ビットのあるもの) が同じ物理学の異なるバージョンであることを示唆していますが、この二重性をどのように概念化するかは依然として謎のままです。
科学界では、研究結果の基本的な意味についてさまざまな意見がある可能性があります。しかし重要なのは、実験におけるホログラフィック ワームホールは、私たちの宇宙の時空とは異なる時空で構成されているということです。この実験が、私たちが住んでいる時空もホログラフィックであることをさらに証明するかどうかは議論の余地がある。
ジャフェリス氏は次のように述べています。「この一次元のワームホールがシカモア チップから生じるのと同じように、宇宙の重力はいくつかの量子ビットから生じると思います。しかし、私たちは完全には確信していません」
背景AdS/CFTの対応は、次のような一連の調査の末に発見されました。質問 。単一の空間領域に収容できる情報の最大量はどれくらいですか?データセンターに保存できる情報の量を誰かがエンジニアに尋ねたら、おそらく答えは「データセンター内のメモリ チップの数と種類によって決まります」ということでしょう。しかし、驚くべきことに、データセンター内にあるものは最終的にはそれほど重要ではありません。データセンターにますます多くのメモリチップと高密度の電子機器を詰め込んでいくと、データセンターは最終的に崩壊して事象の地平線の背後に消えるブラックホールになるでしょう。
ジェイコブ・ベッケンシュタインやスティーブン・ホーキング博士などの物理学者がブラックホールの情報量を計算しようとしたとき、それがブラックホールではなく事象の地平線の面積によって与えられることに驚きました。のボリューム。事象の地平面にはブラックホール内部の情報が書き込まれているようです。具体的には、ブラックホールの事象の地平線は、Aという小さな単位の面積(各単位は「プランク領域」と呼ばれ、2.6121×10^-70平方メートル)でレイアウトでき、最大A/ 4ビットの情報。この限界は「ベケンシュタイン・ホーキング境界」と呼ばれます。
この発見は、領域が保持できる情報の最大量は必ずしもその体積に比例するのではなく、量子情報を示唆する領域の境界の表面積に比例することを示しています。私たちの日常経験の三次元世界との興味深い関係。この関係は、量子情報 (量子ビット) から物質 (それ) がどのように現れるかを説明する「量子ビットからのそれ」というフレーズに要約されています。
通常の時空ではこの関係を形式化することは困難ですが、最近の研究では、「反ド・シッター空間」(反ド・ジッター空間)として知られる双曲幾何学をもつ仮想宇宙に向けて大きな進歩が見られました。シッター空間)では、量子重力理論の構築がより自然になります。
反ド・ジッター空間では、重力が作用する空間の体積の記述は、その体積を囲む境界、つまり空間内のすべての物体にエンコードされていると考えることができます。境界線には対応する記述があり、その逆も同様です。この情報の対応関係は「ホログラフィック原理」と呼ばれ、ベケンシュタインとホーキング博士の観察にインスピレーションを得た一般原理です。

AdS/CFT 対応により、物理学者は空間内のオブジェクトを表面上の相互作用する量子ビットの特定の集合に接続できるようになります。つまり、境界の各領域は、時空の特定の領域の内容を(量子情報で)エンコードし、任意の場所にある物質を量子情報から「構築」できるようにします。これにより、量子プロセッサが量子ビットを直接操作できるようになり、空間と時間の物理学についての洞察が得られます。量子コンピューターのパラメーターを慎重に定義して特定のモデルをシミュレートすることで、ブラック ホールを研究したり、さらに一歩進んで、相互接続された 2 つのブラック ホール (「ワームホール」または「アインシュタイン - ローゼン ブリッジ」として知られる構成) を研究したりすることができます。 」。
実験室における量子重力
Google の研究者は、これらのアイデアを Sycamore プロセッサに実装することを計画しており、通過可能なワームホールと同等の量子システムを構築しました。この実験では、量子情報の言語を空間と時間の物理学に変換するホログラフィック原理を使用して、粒子をワームホールの片側に落下させ、反対側から出現する様子を観察します。
最近の研究で、ダニエル・ジャフェリス、ピン・ガオ、アーロン・ウォールは、通過可能なワームホールの可能性を実証しました。ワームホールは長い間 SF の主題でしたが、「想像力に基づいて」構築されたワームホールは、そこを通過する粒子によって崩壊します。
研究者らは、光の速度で伝わる時空の変形である負のエネルギー衝撃波が、ワームホールを十分に長く開くことでこの問題を解決できることを示しました。それを旅します。通過可能なワームホール内の負のエネルギーの存在は、真空エネルギーが密集したプレートを押し合わせるカシミール効果の負のエネルギーに似ています。どちらの場合も、量子力学により、空間内の特定の場所のエネルギー密度が正または負になることが可能です。一方、ワームホールがポジティブなエネルギーの衝撃波を受けた場合、情報は一切通過できなくなります。
ホログラフィック原理を使用してワームホールを作成する最も単純な応用には、非常に多くの量子ビットが必要です。実際、理論物理学者が示した紙と鉛筆の解決策に近づくには、この解決策には多くの量子ビットが必要です。量子ビットの。量子ビットの数が減少するにつれて、追加の修正が必要になりましたが、現在でもその修正は不明です。限られた数の量子コンピューター上に通過可能なワームホールを構築するには、新しいアイデアが必要です。
研究者の一人であるズロカパ氏は、深層学習のアイデアを使用して、重力物理学の重要な側面を保持する小さな量子システムを設計しました。ニューラル ネットワークは、ネットワークの各層の勾配を直接計算することでパラメーターを最適化する方法であるバックプロパゲーションによってトレーニングされます。ニューラル ネットワークのパフォーマンスを向上させ、トレーニング データ セットの過適合を防ぐために、機械学習の研究者は、できる限り多くの重みを設定することでネットワーク内の情報の詳細を制限しようとするスパース化などの多数の手法を使用しています。ゼロに。
 Alex Zlokapa は MIT の大学院生で、学部生としてワームホール プロジェクトに参加しました。研究の中で、彼はワームホール プロトコルを Google の量子コンピュータで実行できるほど単純化する方法を発見しました。出典: クォンタムマガジン。
Alex Zlokapa は MIT の大学院生で、学部生としてワームホール プロジェクトに参加しました。研究の中で、彼はワームホール プロトコルを Google の量子コンピュータで実行できるほど単純化する方法を発見しました。出典: クォンタムマガジン。
#同様に、ワームホールを作成するには、研究者は大規模な量子システムから始めて、それをニューラル ネットワークのように扱います。バックプロパゲーションはシステムのパラメータを更新して重力特性を維持し、スパース化はシステムのサイズを縮小します。彼らは機械学習を適用して、重力の重要な特徴を 1 つだけ保持するシステムを学習しました。それは、負のエネルギー衝撃波を使用することの重要性です。トレーニング データ セットは、負のエネルギーで開いたワームホールと、正のエネルギーで崩壊したワームホールを通って移動する粒子のダイナミクスを比較します。学習されたシステムがこの非対称性を確実に保持することにより、ワームホールのダイナミクスと一致する疎なモデルが得られました。

研究者らは、新しい量子システムに対して多くのテストを実施し、異なるエネルギーの衝撃波によって引き起こされる特性を超えた重力挙動を示すかどうかを確認しました。たとえば、量子力学的効果はさまざまな方法で量子システムに情報を伝達できますが、ワームホールを含む空間と時間を移動する情報は因果的に一貫していなければなりません。この特徴と他の特徴は古典的なコンピューターで検証され、量子システムの力学がホログラフィック原理の辞書による重力の説明と一致していることが確認されました。
通過可能なワームホールを実験として量子プロセッサに実装することは、非常にデリケートなプロセスです。量子ビット間の情報伝達の微視的なメカニズムは非常に混沌としています。水中で渦を巻くインク滴を想像してください。粒子がワームホールに落ちると、その情報はホログラムの量子システム全体に塗りつぶされます。負のエネルギー衝撃波が機能するためには、情報の破壊が「完璧なサイズの巻き」として知られる特別なパターンに従う必要があります。
粒子が負のエネルギー衝撃波に衝突した後、カオス パターンは事実上逆に作用します。粒子がワームホールから出現すると、あたかも液滴が元の乱流を完全に元に戻して拡散し、再結成する。任意の時点で小さなエラーが発生した場合、カオス的な力学は元に戻らず、粒子はワームホールを通過できなくなります。

研究者らは、Sycamore 量子プロセッサで、負と正のエネルギー衝撃波が適用されたときにシステムの片側からどのくらいの量子情報が転送されるかを測定しました。反対側に渡ります。彼らは、2 つのエネルギー間にわずかな非対称性を観察し、通過可能なワームホールの重要な特徴を示しました。このプロトコルはノイズに敏感であるため、信号を測定するには Sycamore プロセッサの低いエラー率が重要です。1.5 倍のノイズでも信号は完全にマスクされます。
Outlook
重力は、複雑な物理理論を探索する量子コンピュータのユニークな能力の一例にすぎません。量子プロセッサは、時間結晶、量子カオス、化学についての洞察を提供する可能性があります。ワームホールのダイナミクスに関するこの研究は、量子プロセッサを使用して基礎物理学を発見するための一歩を表しています。
量子デバイスが改良され続けるにつれて、エラー率が低下し、チップが大型化することで、研究者は重力現象をより深く調査できるようになります。周囲の世界に関する重力データを記録する実験とは異なり、量子コンピューターは量子重力理論を探索するためのツールを提供します。将来的には、量子コンピューターは、現在のモデルを超えた将来の量子重力理論の理解を発展させるのに役立つでしょう。
以上が「タイムトラベル」は実現するのか?科学者が最初の「ワームホール」を作成し、ネイチャー誌の表紙に登場の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 迅速なエンジニアリングにおける思考のグラフは何ですかApr 13, 2025 am 11:53 AM
迅速なエンジニアリングにおける思考のグラフは何ですかApr 13, 2025 am 11:53 AM導入 迅速なエンジニアリングでは、「思考のグラフ」とは、グラフ理論を使用してAIの推論プロセスを構造化および導く新しいアプローチを指します。しばしば線形sを含む従来の方法とは異なります
 Genaiエージェントとの電子メールマーケティングを組織に最適化しますApr 13, 2025 am 11:44 AM
Genaiエージェントとの電子メールマーケティングを組織に最適化しますApr 13, 2025 am 11:44 AM導入 おめでとう!あなたは成功したビジネスを運営しています。ウェブページ、ソーシャルメディアキャンペーン、ウェビナー、会議、無料リソース、その他のソースを通じて、毎日5000の電子メールIDを収集します。次の明白なステップはです
 Apache Pinotによるリアルタイムアプリのパフォーマンス監視Apr 13, 2025 am 11:40 AM
Apache Pinotによるリアルタイムアプリのパフォーマンス監視Apr 13, 2025 am 11:40 AM導入 今日のペースの速いソフトウェア開発環境では、最適なアプリケーションパフォーマンスが重要です。応答時間、エラーレート、リソース利用などのリアルタイムメトリックを監視することで、メインに役立ちます
 ChatGptは10億人のユーザーにヒットしますか? 「わずか数週間で2倍になりました」とOpenai CEOは言いますApr 13, 2025 am 11:23 AM
ChatGptは10億人のユーザーにヒットしますか? 「わずか数週間で2倍になりました」とOpenai CEOは言いますApr 13, 2025 am 11:23 AM「ユーザーは何人いますか?」彼は突き出した。 「私たちが最後に言ったのは毎週5億人のアクティブであり、非常に急速に成長していると思います」とアルトマンは答えました。 「わずか数週間で2倍になったと言った」とアンダーソンは続けた。 「私はそのprivと言いました
 PIXTRAL -12B:Mistral AI'の最初のマルチモーダルモデル-Analytics VidhyaApr 13, 2025 am 11:20 AM
PIXTRAL -12B:Mistral AI'の最初のマルチモーダルモデル-Analytics VidhyaApr 13, 2025 am 11:20 AM導入 Mistralは、最初のマルチモーダルモデル、つまりPixtral-12B-2409をリリースしました。このモデルは、Mistralの120億個のパラメーターであるNemo 12bに基づいて構築されています。このモデルを際立たせるものは何ですか?これで、画像とTexの両方を採用できます
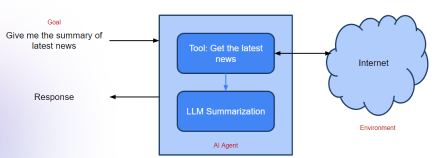 生成AIアプリケーションのエージェントフレームワーク - 分析VidhyaApr 13, 2025 am 11:13 AM
生成AIアプリケーションのエージェントフレームワーク - 分析VidhyaApr 13, 2025 am 11:13 AMクエリに応答するだけでなく、情報を自律的に収集し、タスクを実行し、テキスト、画像、コードなどの複数のタイプのデータを処理するAIを搭載したアシスタントがいることを想像してください。未来的に聞こえますか?これでa
 金融セクターにおける生成AIの応用Apr 13, 2025 am 11:12 AM
金融セクターにおける生成AIの応用Apr 13, 2025 am 11:12 AM導入 金融業界は、効率的な取引と信用の可用性を促進することにより経済成長を促進するため、あらゆる国の発展の基礎となっています。取引の容易さとクレジット
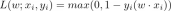 オンライン学習とパッシブアグレッシブアルゴリズムのガイドApr 13, 2025 am 11:09 AM
オンライン学習とパッシブアグレッシブアルゴリズムのガイドApr 13, 2025 am 11:09 AM導入 データは、ソーシャルメディア、金融取引、eコマースプラットフォームなどのソースから前例のないレートで生成されています。この連続的な情報ストリームを処理することは課題ですが、


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

Safe Exam Browser
Safe Exam Browser は、オンライン試験を安全に受験するための安全なブラウザ環境です。このソフトウェアは、あらゆるコンピュータを安全なワークステーションに変えます。あらゆるユーティリティへのアクセスを制御し、学生が無許可のリソースを使用するのを防ぎます。

MantisBT
Mantis は、製品の欠陥追跡を支援するために設計された、導入が簡単な Web ベースの欠陥追跡ツールです。 PHP、MySQL、Web サーバーが必要です。デモおよびホスティング サービスをチェックしてください。

SAP NetWeaver Server Adapter for Eclipse
Eclipse を SAP NetWeaver アプリケーション サーバーと統合します。

SublimeText3 英語版
推奨: Win バージョン、コードプロンプトをサポート!

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)







