100,000 個の方程式を解く必要があった量子問題は、AI によって精度を犠牲にすることなくわずか 4 個の方程式に圧縮されました。

相互作用する電子は、異なるエネルギーや温度でさまざまな特異な現象を示し、周囲の環境を変えると、スピンやペアリングゆらぎなど、新たな集団挙動を示します。電子間のこれらの現象を扱う際に。多くの研究者は、この問題を解決するために繰り込み群 (RG) を使用します。

高次元データの文脈では、機械学習 (ML) テクノロジーとデータ駆動型手法の出現が、量子物理学の研究者の間で大きな関心を呼び起こしています。電子システムの相互作用に使用されています。

この記事では、ボローニャ大学およびその他の機関の物理学者が人工知能を使用して、これまで 100,000 の方程式が必要だった量子問題を、わずか 4 つの方程式で 1 ​​つに圧縮します。すべて正確さを犠牲にすることなく、この研究は本日、Physical Review Letters に掲載されました。

論文アドレス: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.136402

この研究の筆頭著者でボローニャ大学助教授のドメニコ・ディ・サンテ氏は次のように述べています。「私たちはこの巨大なプロジェクトを結合し、機械学習を使用してそれを圧縮して、指一本で数えられるタスク。

この研究では、電子が格子状の格子内を移動するときにどのように動作するかという問題を扱いました。既存の経験によれば、2 つの電子が同じ格子を占有する場合、それらは相互作用します。ハバードモデルとして知られるこの現象は、いくつかの材料の理想的な設定であり、これにより科学者は、電子が抵抗なく材料中を流れる超伝導などの物質の相を作り出すために電子がどのように動作するかを理解することができます。このモデルは、新しい手法をより複雑な量子システムに適用する前に、そのテストの場としても機能します。

2 次元ハバード モデルの概略図

ハバードモデルは単純に見えますが、最先端の計算手法を使用して少数の電子を処理する場合でも、多くの計算能力が必要です。これは、電子が相互作用すると量子力学的にもつれが生じるためであり、たとえ電子が格子内で遠く離れた位置にあったとしても、2 つの電子を独立して扱うことはできないため、物理学者はこれらすべてを同時に扱う必要があります。電子を一度に。電子の数が増えれば増えるほど、量子力学的もつれも多くなり、計算の難易度は指数関数的に増加します。

量子システムを研究する一般的な方法は、繰り込み群です。数学的装置として、物理学者はハバード モデルなどのシステムの動作を観察するためにこれを使用します。残念なことに、繰り込みグループは、電子間の考えられるすべての結合を記録します。これには、解く必要のある数千、数十万、さらには数百万の独立した方程式が含まれる可能性があります。その上、方程式は複雑です。各方程式は相互作用する電子のペアを表します。

Di Sante チームは、ニューラル ネットワークと呼ばれる機械学習ツールを使用して繰り込みグループをより管理しやすくできないかと考えました。

ニューラル ネットワークの場合、まず研究者は機械学習手順を使用してフルサイズの繰り込み群への接続を確立します。次に、ニューラル ネットワークは、適切な値が見つかるまでこれらの接続の強度を調整します。 small 元の非常に大きな繰り込み群と同じ解をもたらす方程式のセット。最終的に方程式は 4 つになります。方程式は 4 つしかありませんが、プログラムの出力はハバード モデルの物理を捉えています。

Di Sante 氏は次のように述べています。「ニューラル ネットワークは本質的に、隠れたパターンを発見できるマシンであり、この結果は私たちの予想を上回りました。」

機械学習プログラムのトレーニングには大量のコンピューティング能力が必要なため、完了までに数週間かかりました。幸いなことに、彼らのプログラムはすでに稼働しており、最初からやり直すことなく、いくつかの調整を行うだけで他の問題を解決できるということです。

ディ・サンテ氏は、将来の研究の方向性について語る際、より複雑な量子システムにおいて新しい手法がどれほど効果的であるかを検証する必要があると述べた。さらに、ディ・サンテ氏は、宇宙論や神経科学など、繰り込み群に関する他の分野でもこの技術を使用できる大きな可能性があると述べています。

論文概要

広く研究されている二次元 t-t' ハバード モデルのスケール依存の 4 次元関数繰り込み群 (fRG) 流れ特性を平方根で説明します。頂点関数を使用して、研究者らはデータ駆動型の次元削減を実行しました。彼らは、低次元潜在空間における神経正微分方程式 (NODE) ソルバーに基づく深層学習アーキテクチャが、ハバード モデルのさまざまな磁気および d 波超伝導状態を記述する fRG ダイナミクスを効率的に学習できることを実証しました。

研究者らはさらに、動的モード分解解析を提案しました。これにより、fRG のダイナミクスを捉えるにはいくつかのモードで実際に十分であることが確認できます。この研究は、人工知能を使用して関連する電子の 4 頂点関数のコンパクトな表現を抽出する可能性を示しています。これは、最先端の場の量子理論手法を首尾よく実装し、多電子問題を解決するための最も重要な目標です。

fRG の基本オブジェクトは頂点関数 V(k_1, k_2, k_3) で、原理的には 3 つの連続運動量変数からなる関数の計算と保存が必要です。特定の理論パターンを研究することにより、2 次元ハバード モデルは銅酸化物および広範囲の有機導体に関連すると考えられます。我々は、低次元表現が高次元頂点関数の fRG フローを捕捉できることを示します。

ハバード モデルの fRG 基底状態。研究者が考えた微視的なハミルトニアンは次の式(1)に示されます。

ハバード モデルの 2 粒子特性は、温度流の 1 ループ fRG スキームを通じて研究されます。ここで、 のRGフローは以下の式(2)に示されます。

#次の図 1 a) は、2 粒子頂点関数 V^Λ の 1 リング fRG 流れ方程式をグラフで表したものです。

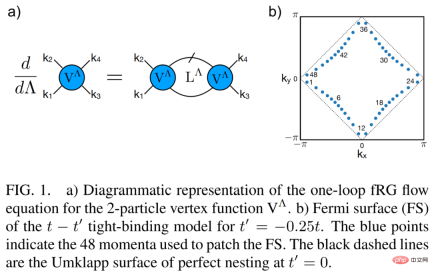# 次に、ディープ ラーニング fRG を見てみましょう。以下の図 2 b) に示すように、fRG フローが強い結合と 1 リング近似分解に向かう前の 2 粒子頂点関数の

結合を調べることで、研究者らは次のことを認識しました。そのうちのいずれかが限界状態に留まるか、どちらかが RG フローの下では無関係になります。 研究者は、現在の高次元問題に適したパラメータ化された NODE アーキテクチャに基づいた柔軟な次元削減スキームを実装しています。この方法は、ディープ ニューラル ネットワークに焦点を当てて、以下の図 2 a) に示されています。 。

# 以下の図 3 は、インターネットの潜在空間学習特性の fRG ダイナミクス中の NODE ニューラルとして、統計的に高度に相関した 3 つの潜在空間表現 z を示しています。

詳細については、元の論文を参照してください。

以上が100,000 個の方程式を解く必要があった量子問題は、AI によって精度を犠牲にすることなくわずか 4 個の方程式に圧縮されました。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。