ホームページ >Java >&#&チュートリアル >Java データ構造のヒープを作成する方法
Java データ構造のヒープを作成する方法
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB転載
- 2023-05-15 20:01:04989ブラウズ
ヒープのプロパティ
ヒープは論理的には完全なバイナリ ツリーであり、ヒープは物理的に配列に格納されます。
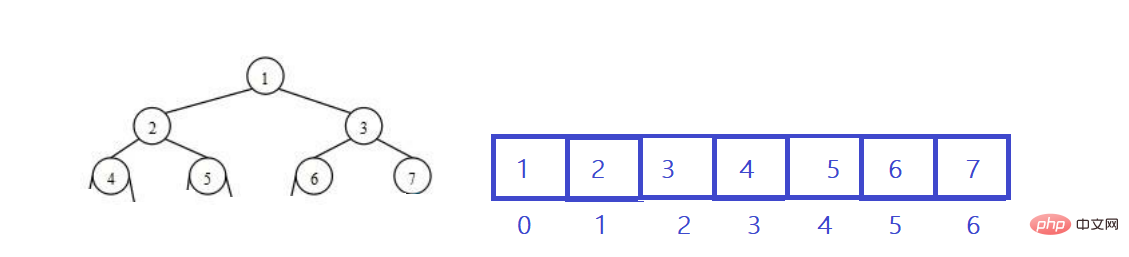
概要: 完全なバイナリ ツリーはレベル順トラバーサルを使用して配列に格納されます。このメソッドの主な用途はヒープ表現です。
そして、父親 (親) の添字がわかっている場合、
then: 左の子 (左) 添字 = 2 * 親 1;
右の子 (右)添字 = 2 * 親 2;
既知の子 (左右の区別なし) (子) 添字、その後:
親 (親) 添字 = (子 - 1) / 2 ;
ヒープの分類
ビッグ ヒープ: ルート ノードが左右の子ノードより大きい (親ノードがその子ノードより大きい) 完全なバイナリ ツリーは、「ヒープ」と呼ばれます。大きなヒープ、大きなルート ヒープ、または最大ヒープ。
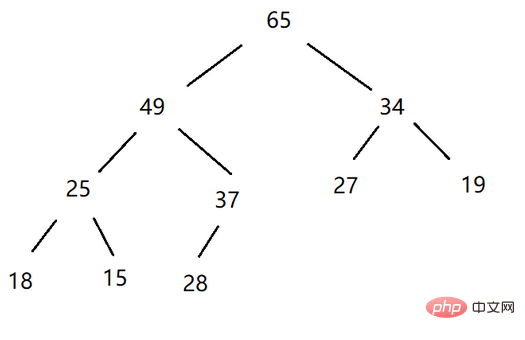
小さなヒープ: ルート ノードが左右 2 つの子ノードより小さい完全なバイナリ ツリーは、小さなヒープと呼ばれます (親ノードはそのノードよりも小さい)子ノード)、小さなルート ヒープ、または最小ヒープ。
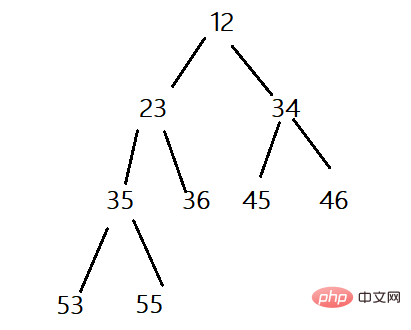
ヒープの下方調整
これで、論理的に完全なバイナリ ツリーである配列ができました。下方調整アルゴリズムを使用できます。ルートノードを小さな山や大きな山に合わせて調整します。下方調整アルゴリズムには前提条件があります。左右のサブツリーは、調整する前にヒープでなければなりません。
小さなヒープを例に挙げます:
1. まず、左右の子ノードを比較して最小値を取得します。
2. 小さい子ノードと親ノードを比較し、子ノードが親ノードより小さい場合は交換し、そうでない場合は交換しません。
3. このサイクルが繰り返され、子ノードの添字が範囲外の場合は、終端に達したことを意味し、終了となります。
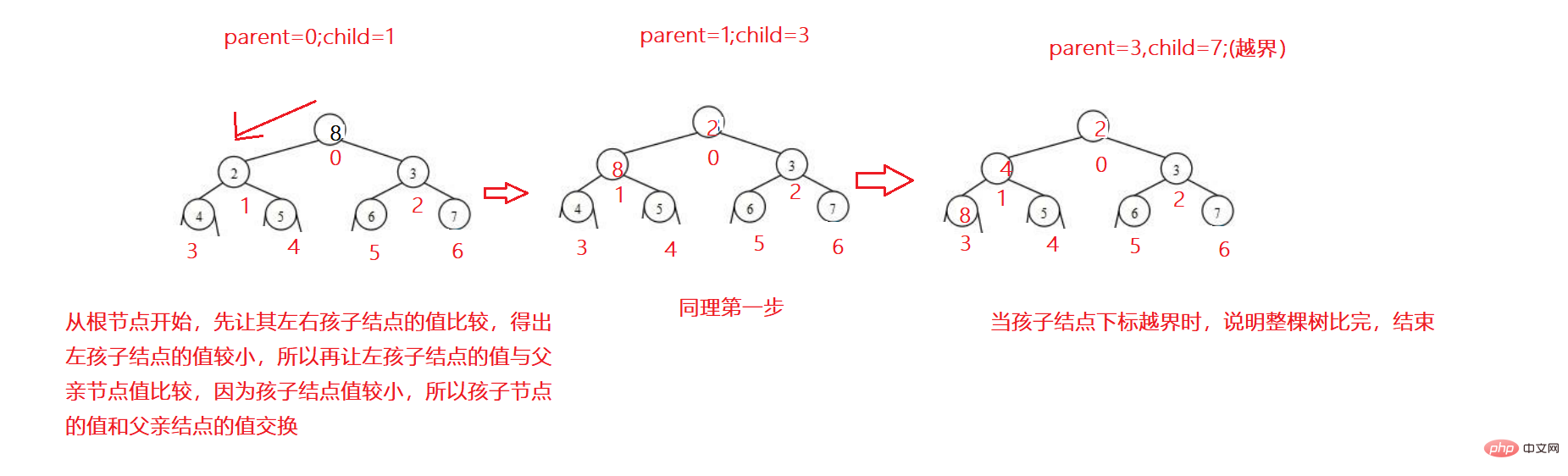
コード例:
//parent: 每棵树的根节点
//len: 每棵树的调整的结束位置
public void shiftDown(int parent,int len){
int child=parent*2+1; //因为堆是完全二叉树,没有左孩子就一定没有右孩子,所以最起码是有左孩子的,至少有1个孩子
while(child<len){
if(child+1<len && elem[child]<elem[child+1]){
child++;//两孩子结点比较取较小值
}
if(elem[child]<elem[parent]){
int tmp=elem[parent];
elem[parent]=elem[child];
elem[child]=tmp;
parent=child;
child=parent*2+1;
}else{
break;
}
}
}ヒープの作成
配列が与えられた場合、この配列は論理的に完全なバイナリ ツリーとみなすことができます。しかし、それはまだヒープではありません (左右のサブツリーは両方とも大きくも小さくもありません)。次に、アルゴリズムを使用してそれをヒープ (大または小) に構築します。どうすればいいですか?ここでは、最後の非リーフ ノードの最初のサブツリーから調整を開始し、ルート ノードのツリーまで調整してから、それをパイルに調整できます。ここでは先ほど書いた下方修正を使います。
public void creatHeap(int[] arr){
for(int i=0;i<arr.length;i++){
elem[i]=arr[i];
useSize++;
}
for(int parent=(useSize-1-1)/2;parent>=0;parent--){//数组下标从0开始
shiftDown(parent,useSize);
}
}ヒープは完全なバイナリ ツリーであり、完全なバイナリ ツリーでもあり、完全なバイナリ ツリーであるため、ヒープを構築する際の空間複雑さは O(N) です。完全なバイナリ ツリーを使用します (最悪の場合)それを証明するために。
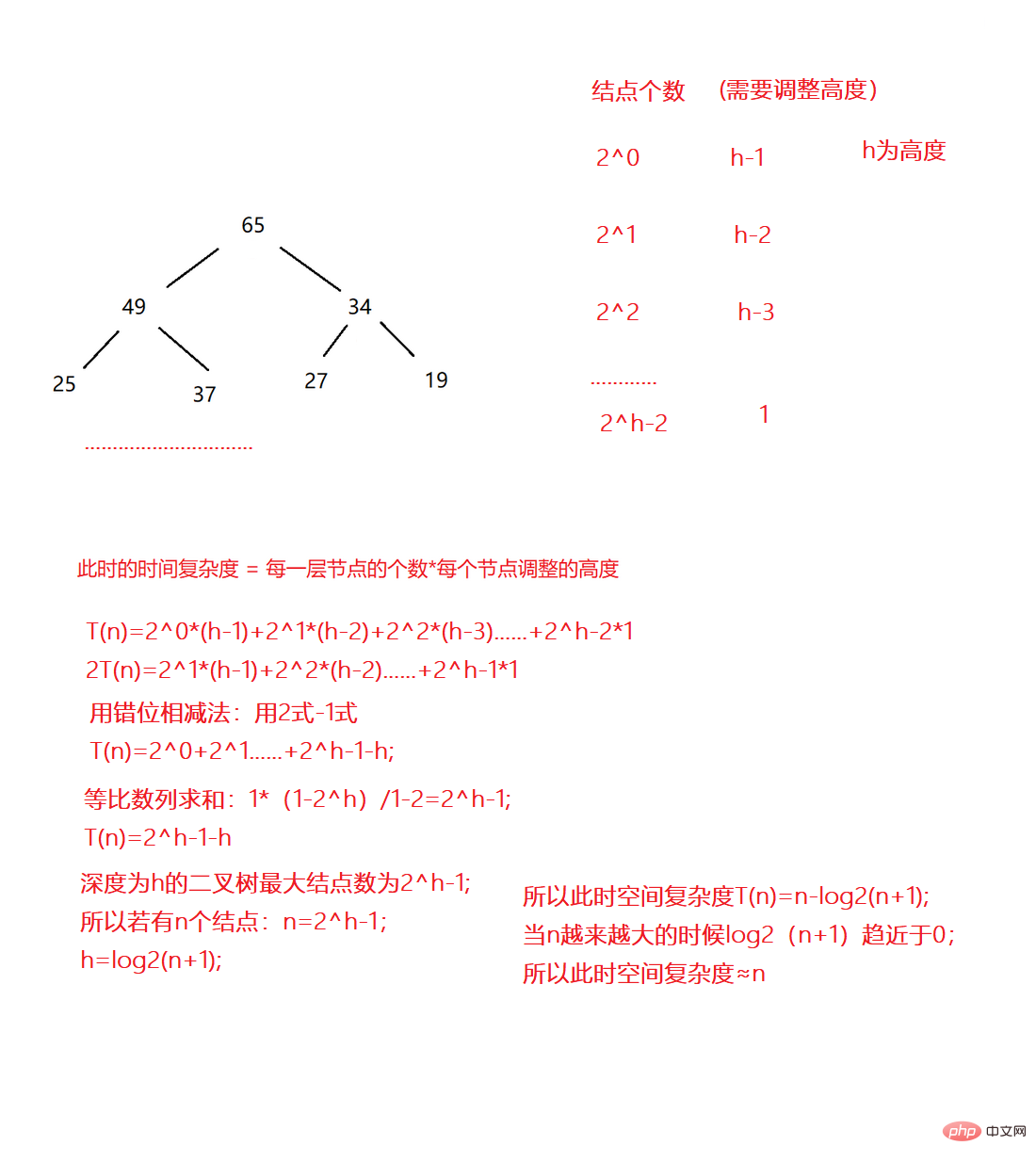
ヒープを上方に調整する必要があります
これでヒープができました。ヒープの最後にデータを挿入して、次のように調整する必要があります。ヒープ構造はまだ維持されているため、これは上方調整です。
大規模なヒープを例に挙げます:
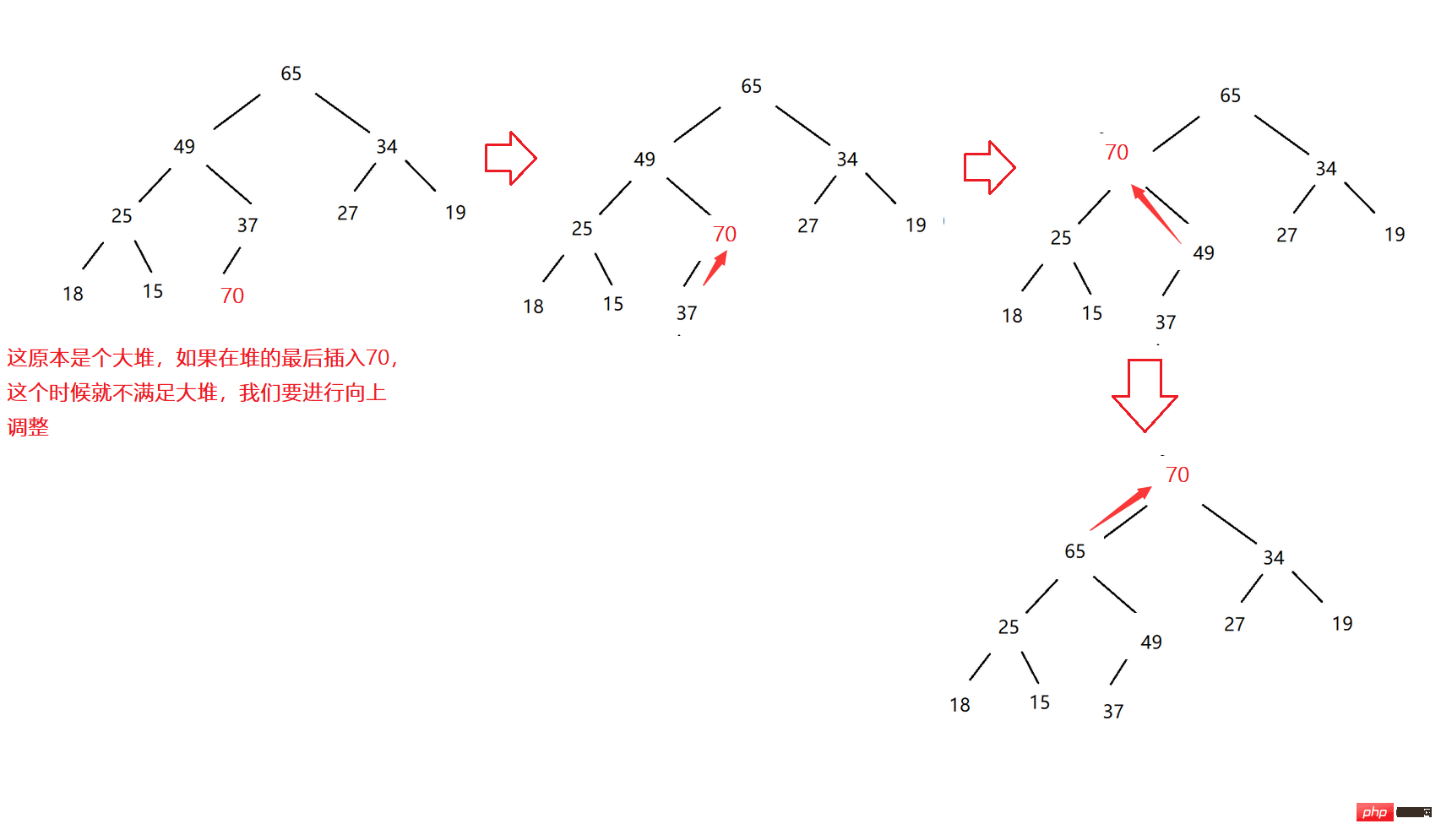
コード例:
public void shiftup(int child){
int parent=(child-1)/2;
while(child>0){
if(elem[child]>elem[parent]){
int tmp=elem[parent];
elem[parent]=elem[child];
elem[child]=tmp;
child=parent;
parent=(child-1)/2;
}else{
break;
}
}
}ヒープに対する一般的な操作
Enter queue
ヒープに要素を追加するには、要素を最後の位置に追加してから上方に調整します。
public boolean isFull(){
return elem.length==useSize;
}
public void offer(int val){
if(isFull()){
elem= Arrays.copyOf(elem,2*elem.length);//扩容
}
elem[useSize++]=val;
shiftup(useSize-1);
}Dequeue
ヒープから要素を削除するには、ヒープの先頭の要素を最後の要素と交換し、配列全体のサイズを 1 つ減らして、最後に次のように下方調整します。 stack.要素の最上位を削除します。
public boolean isEmpty(){
return useSize==0;
}
public int poll(){
if(isEmpty()){
throw new RuntimeException("优先级队列为空");
}
int tmp=elem[0];
elem[0]=elem[useSize-1];
elem[useSize-1]=tmp;
useSize--;
shiftDown(0,useSize);
return tmp;
}チームの最初の要素を取得
public int peek() {
if (isEmpty()) {
throw new RuntimeException("优先级队列为空");
}
return elem[0];
}TopK Question
6 つのデータを与えて、上位 3 つの最大データを見つけます。現時点でヒープをどのように使用すればよいでしょうか?
問題解決のアイデア:
1. 上位 K 個の最大要素を見つけたい場合は、小さなルート ヒープを構築する必要があります。
2. 最初の K 個の最小要素を見つけたい場合は、大規模なルート ヒープを構築する必要があります。
3. K 番目に大きい要素。小さなヒープを構築すると、ヒープの最上位要素が K 番目に大きい要素になります。
4. K 番目に小さい要素。大きなヒープを構築すると、ヒープの最上位要素が K 番目に大きい要素になります。
例
例: 最初の n 番目の最大データを検索
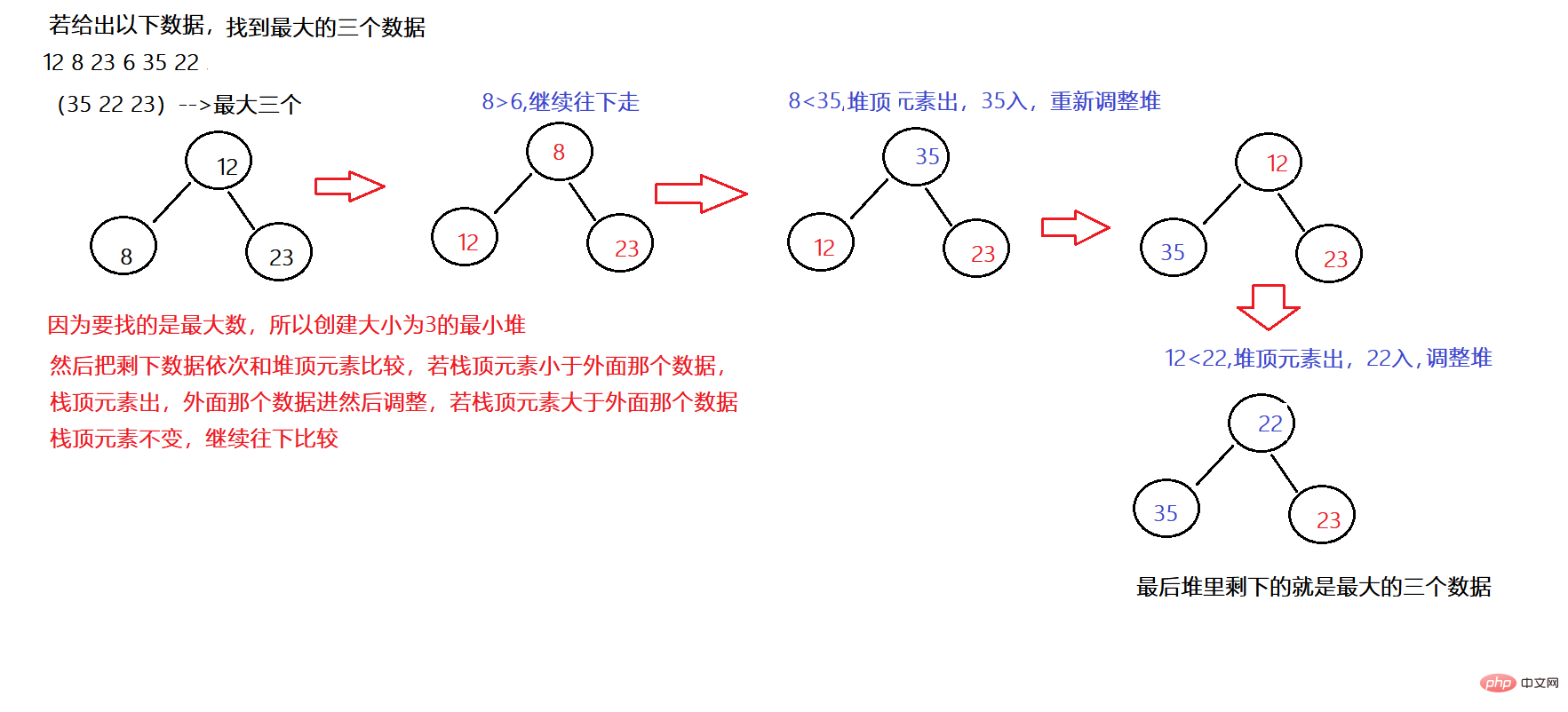
public static int[] topK(int[] array,int k){
//创建一个大小为K的小根堆
PriorityQueue<Integer> minHeap=new PriorityQueue<>(k, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1-o2;
}
});
//遍历数组中元素,将前k个元素放入队列中
for(int i=0;i<array.length;i++){
if(minHeap.size()<k){
minHeap.offer(array[i]);
}else{
//从k+1个元素开始,分别和堆顶元素比较
int top=minHeap.peek();
if(array[i]>top){
//先弹出后存入
minHeap.poll();
minHeap.offer(array[i]);
}
}
}
//将堆中元素放入数组中
int[] tmp=new int[k];
for(int i=0;i< tmp.length;i++){
int top=minHeap.poll();
tmp[i]=top;
}
return tmp;
}
public static void main(String[] args) {
int[] array={12,8,23,6,35,22};
int[] tmp=topK(array,3);
System.out.println(Arrays.toString(tmp));
}結果:
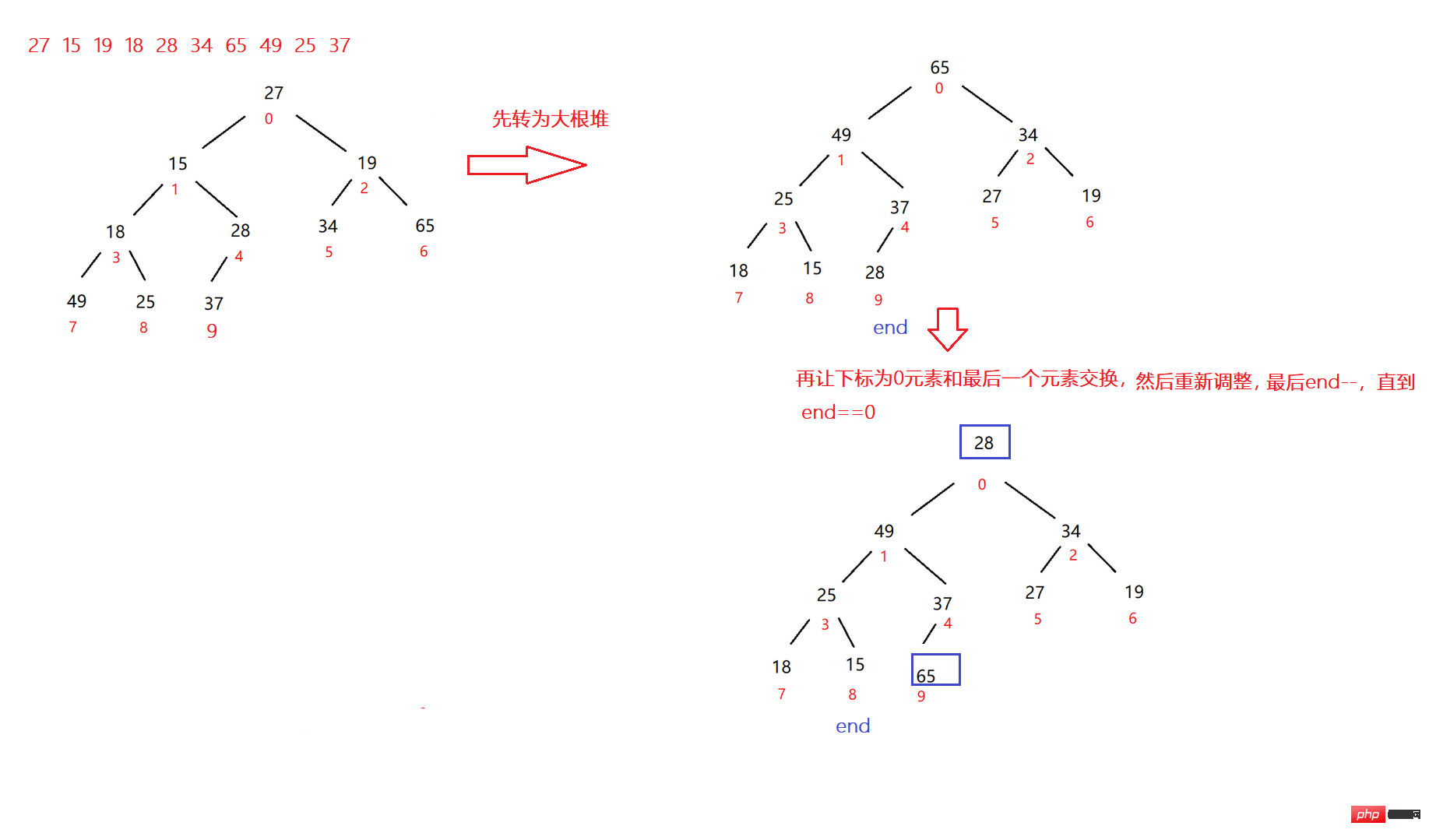
public void heapSort(){
int end=useSize-1;
while(end>0){
int tmp=elem[0];
elem[0]=elem[end];
elem[end]=tmp;
shiftDown(0,end);//假设这里向下调整为大根堆
end--;
}
}以上がJava データ構造のヒープを作成する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

