Java で Kruskal アルゴリズムを実装する方法

はじめに

最小スパニング ツリーを構築するための別のアルゴリズム、つまりクラスカル アルゴリズムがあります。グラフ G=(V, E) を無向接続加重グラフ V={1,2, ... n}; 最小スパニング ツリー T=(V, TE) を仮定します。ツリーの初期状態には n 個のノードのみがあり、エッジのない非接続グラフ T=(V, {}) が含まれます。クラスカルのアルゴリズムは次のように扱います。これらの n ノードは、n 個の分離された接続されたブランチとして扱われます。まず、すべてのエッジを重みに従って小さいものから大きいものまで並べ替えます。次に、T で選択されるエッジの数が n-1 未満の場合は、次のような貪欲な選択を行います。 エッジ (i,j) を選択します。エッジ セット E 内の最小の重みを持つエッジ (i, j) をセット TE に追加してもサイクルが生成されない場合は、エッジ (i, j) をエッジ セット TE に追加します。つまり、エッジ (i 、 j) 2 つのブランチを接続されたブランチにマージする場合、それ以外の場合は、次に短いエッジの選択を続けます。セット E からエッジ (i, j) を削除し、T 内のすべてのノードが同じ接続されたブランチ上に配置されるまで上記の貪欲な選択を続けます。このとき、選択された n-1 個のエッジは、まさにグラフ G の最小全域木 T を構成します。

Kruskal のアルゴリズムは、円を避けるためにセットを使用するという非常に賢い方法を使用しています。結合するために選択したエッジの開始点と終了点が両方とも T セット内にある場合、ループであると結論付けることができます。が形成され、変更された 2 つのノードは同じコレクションに属することはできません。

アルゴリズムのステップ

1 初期化。すべてのエッジを重みの昇順にソートし、各ノード セット番号を独自の番号に初期化します。

2 ソートされた順序で重みが最小のエッジ (u, v) を選択します。

3 ノード u と v が 2 つの異なる接続されたブランチに属している場合、エッジ (u, v) をエッジ セット TE に追加し、2 つの接続されたブランチをマージします。

4 選択したエッジの数が n-1 未満の場合はステップ 2 に進み、そうでない場合はアルゴリズムが終了します。

1. 施工後の写真

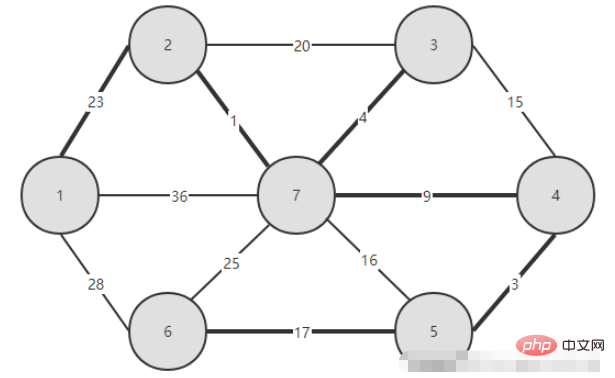
#2. コード

package graph.kruskal;
 
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;
 
public class Kruskal {
    static final int N = 100;
    static int fa[] = new int[N];
    static int n;
    static int m;
 
    static Edge e[] = new Edge[N * N];
    static List<Edge> edgeList = new ArrayList();
 
    static {
        for (int i = 0; i < e.length; i++) {
            e[i] = new Edge();
        }
    }
 
    // 初始化集合号为自身
    static void Init(int n) {
        for (int i = 1; i <= n; i++)
            fa[i] = i;
    }
 
    // 合并
    static int Merge(int a, int b) {
        int p = fa[a];
        int q = fa[b];
        if (p == q) return 0;
        for (int i = 1; i <= n; i++) { // 检查所有结点，把集合号是 q 的改为 p
            if (fa[i] == q)
                fa[i] = p; // a 的集合号赋值给 b 集合号
        }
        return 1;
    }
 
    // 求最小生成树
    static int Kruskal(int n) {
        int ans = 0;
        Collections.sort(edgeList);
        for (int i = 0; i < m; i++)
            if (Merge(edgeList.get(i).u, edgeList.get(i).v) == 1) {
                ans += edgeList.get(i).w;
                n--;
                if (n == 1)//n-1次合并算法结束
                    return ans;
            }
        return 0;
    }
 
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        m = scanner.nextInt();
        Init(n);
        for (int i = 1; i <= m; i++) {
            e[i].u = scanner.nextInt();
            e[i].v = scanner.nextInt();
            e[i].w = scanner.nextInt();
            edgeList.add(e[i]);
        }
        System.out.println("最小的花费是：" + Kruskal(n));
    }
}
 
class Edge implements Comparable {
    int u;
    int w;
    int v;
 
    @Override
    public int compareTo(Object o) {
        if (this.w > ((Edge) o).w) {
            return 1;
        } else if (this.w == ((Edge) o).w) {
            return 0;
        } else {
            return -1;
        }
    }
}

3. テスト

緑が入力、白が入力出力。

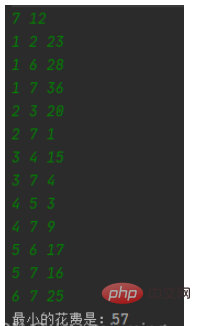
以上がJava で Kruskal アルゴリズムを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。