ホームページ >テクノロジー周辺機器 >AI >盲目的に大きなモデルを追い求めてコンピューティングパワーを蓄積しないでください。 Shen Xiangyang、Cao Ying、Ma Yi は、AI を理解するための 2 つの基本原則、倹約と自己一貫性を提案しました。
盲目的に大きなモデルを追い求めてコンピューティングパワーを蓄積しないでください。 Shen Xiangyang、Cao Ying、Ma Yi は、AI を理解するための 2 つの基本原則、倹約と自己一貫性を提案しました。
- 王林転載
- 2023-05-11 12:22:061645ブラウズ
過去 2 年間で、「多大な努力 (計算能力) で奇跡を生み出すことができる」大規模モデルが、人工知能分野のほとんどの研究者によって追求される傾向になりました。しかし、その背後にある膨大な計算コストとリソース消費の問題が徐々に明らかになり、一部の科学者は大規模モデルを真剣に検討し、積極的に解決策を模索し始めています。新しい研究によると、AI モデルの優れたパフォーマンスの実現は、必ずしもヒープのコンピューティング能力やヒープ サイズに依存するわけではありません。
ディープラーニングは 10 年来ブームになっていますが、この 10 年間の研究と実践の中で、その機会とボトルネックが多くの注目と議論を集めてきたと言わざるを得ません。
そのボトルネックの次元の中で最も目を引くのは、深層学習のブラックボックス特性(解釈可能性の欠如)と「苦労して奇跡的な結果が得られる」(モデルパラメータはコンピューティング能力に対する需要はますます大きくなり、コンピューティングのコストはますます高くなっています)。さらに、モデルの安定性の不足やセキュリティの脆弱性などの問題もあります。
本質的に、これらの問題は、ディープ ニューラル ネットワークの「開ループ」システムの性質によって部分的に引き起こされます。深層学習の B サイドの「呪い」を解くには、単にモデルの規模と計算能力を拡大するだけでは十分ではなく、人工知能システムの基本原理からソースを追跡する必要があります。新しい視点(閉ループなど) 「知性」を理解する。
7 月 12 日、人工知能の分野で著名な中国の 3 人の科学者、馬毅、曹英、舜祥陽が共同で arXiv に「次の原則について」という記事を発表しました。インテリジェンスの出現のための節約と自己一貫性」では、深層ネットワークを理解するための新しいフレームワークである圧縮閉ループ転写を提案しています。
このフレームワークには、倹約性と自己一貫性という 2 つの原則が含まれており、それぞれ AI モデルの学習プロセスで「何を学習するか」と「どのように学習するか」に対応します。は人工知能と自然知能の 2 つの基盤であり、国内外の人工知能研究分野で広く注目を集めています。



いわゆるシンプルさは「何を学ぶか」です。インテリジェントな倹約の原理により、システムは計算効率の高い方法でコンパクトで構造化された表現を取得する必要があります。つまり、インテリジェント システムは、現実の感覚データの有用な構造をシンプルかつ効率的にシミュレートできる限り、世界を記述するあらゆる構造化モデルを使用できます。システムは、基本的で普遍的で、計算と最適化が容易な指標を使用して、学習モデルの品質を正確かつ効率的に評価できなければなりません。
ビジュアル データ モデリングを例に挙げると、倹約原則は次の目標を達成するために (非線形) 変換を見つけようとします:
圧縮: 高次元の感覚データ x 低次元表現 z にマップします;
線形化: 非線形部分多様体上に分布する各タイプのオブジェクトを線形部分空間にマップします;
スカリフィケーション: 異なるクラスを部分空間に変換します独立した、または最大限に一貫性のない基盤。
つまり、高次元空間内の一連の低次元部分多様体上に位置する可能性がある実世界のデータは、独立した低次元線形部分空間系列に変換されます。このモデルは「線形識別表現」(LDR) と呼ばれ、その圧縮プロセスを図 2 に示します。感覚データは、通常、多くの非線形低次元部分多様体に分散され、部分多様体と同じ次元を持つ一連の独立した線形部分空間に分散されます。
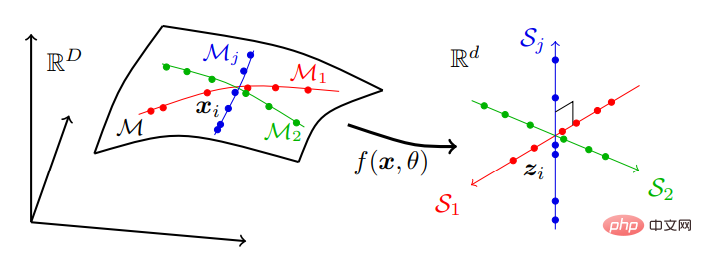

過去 10 年間にわたる人工ニューラル ネットワークの「進化」は、ディープ ネットワーク自体の役割が (勾配ベースの) 反復最適化を実行してデータを圧縮、線形化し、スパース化することであることがわかれば、理解しやすく、特に役立ちます。 Yu 氏は、MLP から CNN、ResNet、Transformer に至るまで、人間による選択プロセスでは少数の AI システムだけが目立つ理由を説明します。
対照的に、ニューラル アーキテクチャ検索などのネットワーク構造のランダム検索では、一般的なタスクを効果的に実行できるネットワーク アーキテクチャは生成されません。彼らは、成功したアーキテクチャは、データ圧縮の反復最適化スキームのシミュレーションにおいてますます効果的かつ柔軟になっていると仮説を立てています。これは、前述した ReduNet と ResNet/ResNeXt の類似点によって例示できます。もちろん、他にも多くの例があります。
自己一貫性
自己一貫性とは、「学習方法」に関するものです。つまり、自律型インテリジェント システムは、観察されたデータとデータを最小限に抑えることによって学習します。再現者は、外界を観察するための最も自己矛盾のないモデルを見つけます。
倹約の原則だけでは、学習モデルが外界のデータを認識する際のすべての重要な情報を確実に捕捉できるわけではありません。
たとえば、クロスエントロピーを最小限に抑えて各クラスを 1 次元の「ワンホット」ベクトルにマッピングすることは、節約的な形式とみなすことができます。優れた分類器を学習する可能性がありますが、学習された特徴はシングルトンに崩壊します。これは、「神経崩壊」として知られています。このようにして学習された特徴には、元のデータを再生成するのに十分な情報が含まれていません。より一般的なクラスの LDR モデルを考慮したとしても、速度削減の目標だけでは、環境特徴空間の正しい寸法が自動的に決定されるわけではありません。特徴空間次元が低すぎる場合、学習されたモデルはデータに過小適合する可能性があり、高すぎる場合、モデルは過適合する可能性があります。
彼らの見解では、知覚の目標は、予測可能なすべての知覚内容を学習することです。インテリジェント システムは、一度生成されると、どんなに頑張っても区別できない圧縮表現から観測データの分布を再生成できなければなりません。
この論文では、自己一貫性と倹約性の 2 つの原則は非常に補完的であり、常に一緒に使用する必要があることを強調しています。自己一貫性だけでは、圧縮や効率の向上は保証されません。
数学的および計算的には、過剰パラメータ化されたモデルを使用してトレーニング データを適合させるか、同じディメンションを持つドメイン間に 1 対 1 のマッピングを確立することで一貫性を確保します。データ分布の本質的な構造を学習します。圧縮を通じてのみ、インテリジェント システムは、高次元の感覚データ内の固有の低次元構造を発見し、将来の使用に備えて最もコンパクトな方法で特徴空間内でこれらの構造を変換して表現することができます。
さらに、圧縮を通じてのみ、過剰なパラメータ化の理由を簡単に理解できます。たとえば、DNN のように、通常、その純粋な目的が次の場合は、数百のチャネルを通じて機能強化を実行します。次元特徴空間での圧縮は過学習につながりません。ブースティングはデータの非線形性を軽減し、圧縮と線形化を容易にします。後続の層の役割は圧縮 (および線形化) を実行することであり、一般に層が多いほど圧縮率は向上します。
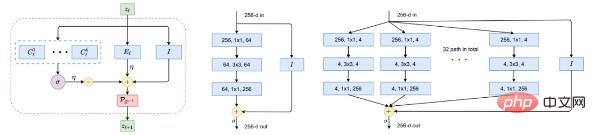
LDR などの構造化表現に圧縮する特殊なケースでは、論文では自動エンコードの一種 (詳細については元の論文を参照) を「転写」と呼んでいます。ここでの難しさは、目標を計算的に扱いやすく、したがって物理的に達成可能にすることです。
レート減少 ΔR は、縮退分布間の明確な一次距離尺度を与えます。ただし、これは部分空間またはガウスの混合に対してのみ機能し、一般分布に対しては機能しません。そして、内部構造化表現 z の分布は、元のデータ x ではなく、部分空間またはガウス分布の混合であるとのみ期待できます。
これは、「自己矛盾のない」表現の学習に関するかなり深い疑問につながります。外部世界の内部モデルが正しいことを検証するために、自律システムは実際に測定する必要があります。データ空間の違い?
#答えは否定的です。 重要なのは、x と x^ を比較するために、エージェントは同じマッピング f を介してそれぞれの内部特徴 z = f(x) と z^ = を比較するだけでよいことを理解することです。 f(x^)、z をコンパクトで構造化します。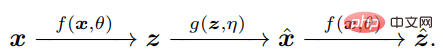
Z 空間における分布の違いの測定は、実際には明確に定義されており、有効です。自然知能には、内部測定を学習するための独立した自律システムがあると言えます。違いは脳ができる唯一のことです。
これにより、図 6 に示すプロセス全体で、「閉ループ」フィードバック システムが効果的に生成されます。
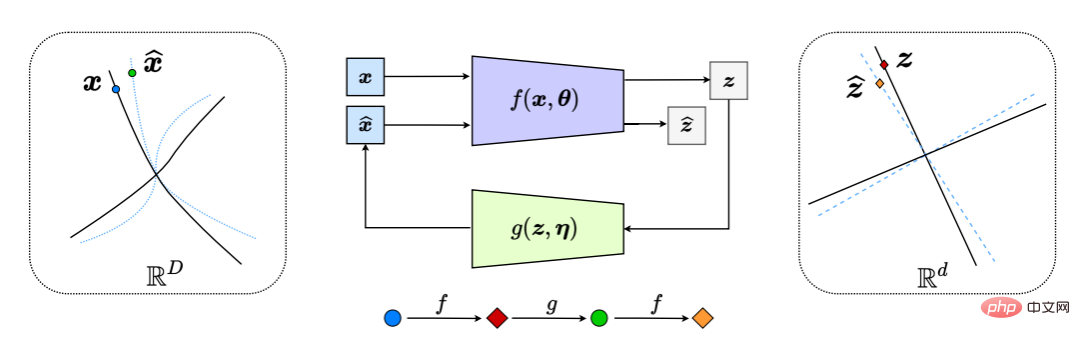
図 6: 非線形データ部分多様体の LDR への圧縮閉ループ転写 (内部的に z と z^ の差を比較して最小化することによる)。これにより、エンコーダー/センサー f とデコーダー/コントローラー g の間で自然なチェイス アンド フライト ゲームが発生し、デコードされた x^ (青の破線) の分布が観測データ x (黒の破線) の分布を追いかけて一致するようになります。実線)。
DNN 分類器 f または生成器 g を個別に学習する一般的な方法は、閉ループ システムのオープンエンド部分を学習するものとして解釈できます (図 6)。この現在一般的なアプローチは、制御分野では問題があり、コストがかかることが長い間知られていた開ループ制御に非常に似ています。そのような部分のトレーニングには、必要な出力 (クラス ラベルなど) の監視が必要です。データ分散の場合、システムは、パラメータやタスクの変更が発生した場合、そのような開ループ システムの展開には本質的に安定性、堅牢性、または適応性が欠けています。たとえば、教師付き環境でトレーニングされた深層分類ネットワークは、新しいデータ カテゴリを使用して新しいタスクを処理するように再トレーニングされると、壊滅的な忘却に見舞われることがよくあります。
対照的に、閉ループ システムは本質的に安定性と適応性が高くなります。実際、ヒントンらは 1995 年にすでにこれを提案しています。識別部分と生成部分は、それぞれ完全な学習プロセスの「覚醒」段階と「睡眠」段階として組み合わせる必要があります。
ただし、ループを閉じるだけでは十分ではありません。
この論文は、知的エージェントには自己批判を通じて自己学習できるよう内部ゲーム メカニズムが必要であると主張しています。ここで続くのは、普遍的に効果的な学習方法としてのゲームの概念です。つまり、敵対的な批判に対して現在のモデルや戦略を繰り返し適用し、それによって閉ループを通じて受け取ったフィードバックに基づいてモデルや戦略を継続的に改善することです。
このようなフレームワーク内では、エンコーダ f は 2 つの役割を果たします。(セクションで実行したように、レート低減 ΔR(Z) を最大化することによってデータ x の表現 z を学習することに加えて) 2.1 の場合)、データ x と生成された x^ の間の差異を積極的に検出する、フィードバック「センサー」としても機能する必要があります。デコーダ g も二重の役割を果たします: これは f によって検出された x と x^ の差にリンクされるコントローラであり、またデコーダでもあり、目標を達成するために全体の符号化レートを最小化しようとします (一定の精度を与える)。
したがって、最適な「節約的」かつ「自己矛盾のない」表現タプル (z, f, g) は、f(θ) と g(η) の間として解釈できます。組み合わせレート削減に基づく効用ではなく、ゼロサム ゲームのポイント:
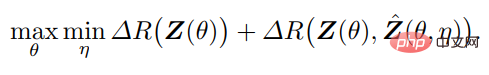
上記の議論は 2 つの原則のパフォーマンスです。監視された状況で。
しかし、論文では、彼らが提案した圧縮閉ループ転写フレームワークは自己監視と自己批判を通じて自己学習できることを強調しています。
さらに、レート削減により学習構造の明示的な (部分空間タイプ) 表現が見つかったため、新しいタスク/データを学習するときに過去の知識を保持しやすくなり、次のように使用できます。自己保存型の一貫した事前分布 (記憶)。
最近の実証研究では、これにより、致命的な忘却に悩まされることなく適切な LDR 表現を段階的に学習できる、固定メモリを備えた最初の自己完結型ニューラル システムが得られることが示されています。このような閉ループ システムでは、(たとえそうであったとしても) 忘れることは非常にエレガントです。
さらに、古いカテゴリの画像がレビューのために再度システムに供給されると、学習された表現がさらに強化されます。これは人間の記憶の機能と非常によく似ています。ある意味、この制約された閉ループの定式化は、これらの特性が脳にとって理想的であると仮定すると、視覚記憶の形成がベイズ的で適応的であることを本質的に保証します。
図 8 に示すように、この方法で学習された自動エンコードはサンプルの一貫性が良好であることを示すだけでなく、学習された特徴は明確で意味のある局所的な低次元 (薄い) 構造も示します。

図 8: 左: 自動エンコードされた x とデコードされた x^ の比較。右: 10 クラスの教師なし学習特徴の t-SNE、およびいくつかの近傍とそれに関連する画像の視覚化。数百次元の特徴空間から投影された、視覚化された特徴における局所的に薄い (ほぼ 1 次元) 構造に注目してください。
さらに驚くべきことは、トレーニング中にクラス情報が提供されなかった場合でも、部分空間または特徴に関連するブロック対角構造が、クラスで学習された特徴に現れ始めることです (図 9) )!したがって、学習された特徴の構造は、霊長類の脳で観察されるカテゴリ選択領域に似ています。
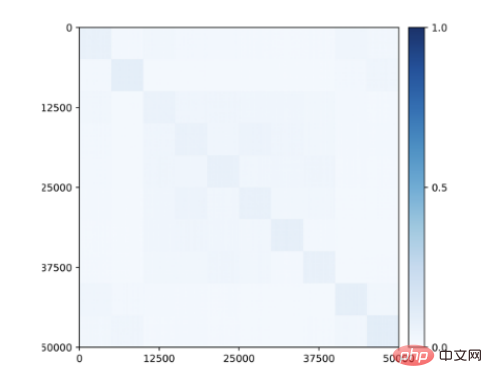
図 9: 閉ループ転写による 10 カテゴリ (CIFAR-10) に属する 50,000 枚の画像の教師なし学習特徴間の相関。クラス一貫性のあるブロック対角構造は、監視なしで出現します。
ユニバーサル ラーニング エンジン: 3D ビジョンとグラフィックスの組み合わせ
論文の要約、シンプルさと自己一貫性から、ディープ ネットワークの役割は、次のものを組み合わせることであることがわかります。外部観察と内部表現、非線形写像モデル。
さらに、この論文は、閉ループ圧縮構造が本質的に遍在し、すべての知的生物に適用できることを強調しています。これは脳 (感覚情報の圧縮) で見られます。脊髄回路(筋肉の動きの圧縮)、DNA(タンパク質の機能情報の圧縮)、その他の生物学的例。したがって、彼らは、圧縮された閉ループ転写がすべての知的行動の背後にある普遍的な学習エンジンである可能性があると信じています。これにより、知的有機体やシステムは、一見複雑で組織化されていない入力から低次元の構造を発見して洗練し、記憶して利用できるコンパクトで組織化された内部構造に変換することができます。
このフレームワークの一般性を説明するために、この論文では、3D 認識と意思決定 (LeCun は自律型インテリジェント システムの 2 つの主要なモジュールと考えています) という 2 つの他のタスクを検討します。この記事は整理されており、3D 認識におけるコンピューター ビジョンとコンピューター グラフィックスの閉ループのみを紹介します。
デイビッド マーによって影響力のある著書『ビジョン』で提案された 3D ビジョンの古典的なパラダイムは、3D 認識タスクをいくつかのモジュール式プロセスに分割する「分割統治」アプローチを提唱しています。 2D 処理 (エッジ検出、輪郭スケッチなど)、中レベルの 2.5D 解析 (グループ化、セグメンテーション、形状、地面など)、高レベルの 3D 再構築 (ポーズ、形状など) および認識 (例:オブジェクト)、そして逆に、圧縮された閉ループ転写フレームワークは「共同構築」のアイデアを促進します。
知覚は圧縮された閉ループ転写ですか?より正確には、世界の物体の形状、外観、さらにはダイナミクスの 3D 表現は、知覚されたすべての視覚的観察をそれに応じて解釈するために私たちの脳によって内部的に開発された、最もコンパクトで構造化された表現である必要があります。そうであれば、これら 2 つの原則は、コンパクトで構造化された 3D 表現が探すべき内部モデルであることを示唆しています。これは、次の図に示すように、コンピュータ ビジョンとコンピュータ グラフィックスをクローズド ループ コンピューティング フレームワーク内で統合できるし、統合する必要があることを意味します。
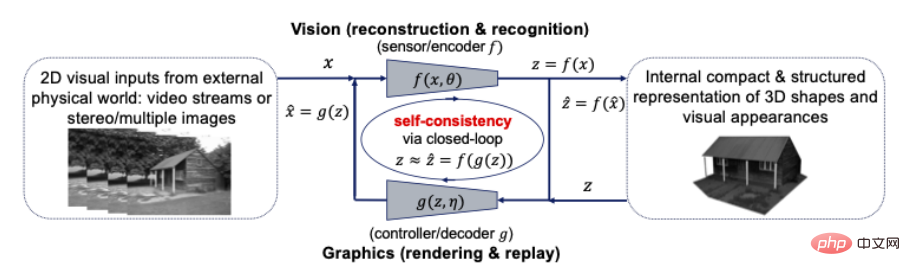
図 10: コンピュータ間の接続ビジョンとグラフィックス 視覚入力のための閉ループ、コンパクトで構造化された 3D モデル
コンピュータ ビジョンは、すべての 2D 視覚入力に対して内部 3D モデルを再構成および識別する前方プロセスとして説明されることがよくありますが、コンピュータ グラフィックスは、内部 3D モデルをレンダリングしてアニメーション化するその逆プロセスを表します。これら 2 つのプロセスを閉ループ システムに直接結合すると、計算上および実用上、多大な利点がもたらされる可能性があります。ジオメトリ、外観、ダイナミクス (疎性や滑らかさなど) のすべての豊富な構造を、最もコンパクトな統合 3D モデルで一緒に使用できます。すべての視覚的入力と一貫性があります。
コンピュータ ビジョンの認識技術は、コンピュータ グラフィックスが形状と外観空間でコンパクトなモデルを構築するのに役立ち、リアルな 3D コンテンツを作成する新しい方法を提供します。一方、コンピュータ グラフィックスの 3D モデリングおよびシミュレーション技術は、コンピュータ ビジョン アルゴリズムによって分析された実際のオブジェクトやシーンの特性や動作を予測、学習、検証できます。ビジュアルおよびグラフィックスのコミュニティは、長い間「総合分析」アプローチを実践してきました。
外観と形状の統一表現?イメージベースのレンダリングは、指定された一連のイメージから学習することによって新しいビューが生成されますが、節約的で自己矛盾のない原則によって、視覚とグラフィックの間のギャップを埋めるための初期の試みと見ることができます。特に、プレノプティック サンプリングは、必要な最小限の画像数 (倹約性) でアンチエイリアス処理された画像 (自己一貫性) を実現できることを示しています。
より広範な知性
知性の神経科学
基本的な知性の原理が脳の設計に情報を与えると期待されるでしょう。インパクト。倹約と自己一貫性の原則は、霊長類の視覚系のいくつかの実験的観察に新たな光を当てました。さらに重要なのは、今後の実験で何を探すべきかを明らかにすることです。
著者チームは、単に内部の節約的で予測的な表現を求めるだけで「自己監視」を達成するのに十分であることを実証し、圧縮された閉ループを通じて学習された最終表現に構造が自動的に現れることを可能にしました。転写。
たとえば、図 9 は、教師なしデータ転写学習がさまざまなカテゴリの特徴を自動的に区別し、脳内で観察されるカテゴリ選択的表現の説明を提供することを示しています。これらの特徴は、霊長類の脳におけるスパースコーディングとサブスペースコーディングの広範な観察に対する合理的な説明も提供します。さらに、視覚データモデリングに加えて、最近の神経科学研究は、脳内で生じる他の構造化表現(「場所細胞」など)も、最も圧縮された方法で空間情報をエンコードした結果である可能性があることを示唆しています。
最大符号化レート削減 (MCR2) 原則は、ベイジアンのフレームワークを提供しようとする認知科学の「自由エネルギー最小化原則」と精神的に似ていると言えます。エネルギー最小化による推論。しかし、フリー エネルギーの一般的な概念とは異なり、レート削減は閉じた形式で表現できるため、計算で扱いやすく、直接最適化することができます。さらに、これら 2 つの原理の相互作用は、正しいモデル (クラス) の自律学習は、最小化だけではなく、このユーティリティの閉ループ最大化ゲームを通じて達成されるべきであることを示唆しています。したがって、彼らは、圧縮された閉ループ転写フレームワークが、ベイズ推論を実際に実装する方法について新しい視点を提供すると信じています。
このフレームワークは、脳によって使用される全体的な学習アーキテクチャを示すものであるとも彼らによって信じられています。脳は、ランダムなネットワークから学習する必要なく、最適化スキームを展開することでフィードフォワードセグメントを構築できます。誤差逆伝播法 。さらに、フレームワークには、学習をガイドする閉ループ フィードバック システムを形成できる補完的な生成部分があります。
最後に、このフレームワークは、「予測コーディング」の脳メカニズムに興味を持つ多くの神経科学者が探し求めていた、とらえどころのない「予測エラー」信号を明らかにします。これは、脳に関連する閉ループ転写の一種です。圧縮 共鳴を生成する計算スキーム: 計算を容易にするために、入力される観測値と生成された観測値の差を表現の最終段階で測定する必要があります。
より高いレベルのインテリジェンスに向けて
Ma Yi らの研究では、圧縮された閉ループ転写はそれと同じであると考えています。 1995 年に Hinton らによって提案された他のフレームワークと比較して、計算処理が容易であり、スケーラブルです。さらに、非線形エンコード/デコード マッピング (ディープ ネットワークとして現れることが多い) の反復学習は、本質的に、外部の未組織の生の感覚データ (視覚、聴覚など) と内部のコンパクトで構造化された表現との間の重要な橋渡しとなる「インターフェイス」を提供します。
しかし、彼らはまた、これら 2 つの原則が必ずしも知性のすべての側面を説明するわけではないことも指摘しました。高レベルの意味論的推論、記号論的推論、または論理的推論の出現と発展の基礎となる計算メカニズムは依然として解明されていません。今日に至るまで、この高度なシンボリック インテリジェンスが継続的な学習から得られるのか、それともハードコーディングする必要があるのかについて議論があります。
3 人の科学者の見解では、部分空間などの構造化された内部表現は、高レベルの意味論的概念または記号概念の出現に必要な中間ステップであり、各部分空間は離散 (オブジェクト)カテゴリ。このような抽象的な離散概念間の他の統計的、因果的、または論理的関係は、各ノードが部分空間/カテゴリを表す、コンパクトで構造化された (たとえば、疎な) グラフとしてさらに単純化してモデル化できます。グラフは自動エンコードを通じて学習され、自己一貫性を確保できます。
彼らは、高度な知能 (共有可能な記号知識による) の出現と発展は、個々のエージェントによって学習されたコンパクトで構造化された表現の上でのみ可能であると推測しています。したがって、彼らは、高度なインテリジェンス(高度なインテリジェンスが存在する場合)の出現のための新しい原理は、インテリジェントシステム間の効果的な情報交換または知識の伝達を通じて探求されるべきであると提案しました。
さらに、高レベルのインテリジェンスには、この記事で提案する 2 つの原則と 2 つの共通点があるはずです。
- 解釈可能性: すべて 原則はすべてである必要があります。測定可能な目標、関連する計算アーキテクチャ、学習表現の構造など、インテリジェントな計算メカニズムをホワイト ボックスとして明らかにするのに役立ちます。
- 計算可能性: 新しいインテリジェンスの原理は、計算的に扱いやすく拡張可能であり、コンピューターまたは自然物理学を通じて達成可能であり、最終的には科学的証拠によって実証されなければなりません。
解釈可能性と計算可能性があってこそ、現在の高価で時間のかかる「試行錯誤」の方法に頼ることなく人工知能の進歩を進め、記述や計算ができるようになります。 「大きいほど良い」という強引なアプローチを単に提唱するのではなく、タスクに必要な最小限のデータとコンピューティング リソースを完成させます。知恵は、最も機知に富んだ人々の特権であるべきではありません。適切な一連の原則があれば、誰でも大小に関わらず、自律性、機能、効率性が最終的に模倣できる、あるいはさらには次世代のインテリジェント システムを設計および構築できるはずです。動物や人間を超えた人類。
論文リンク:
https://arxiv.org/pdf/2207.04630.pdf
以上が盲目的に大きなモデルを追い求めてコンピューティングパワーを蓄積しないでください。 Shen Xiangyang、Cao Ying、Ma Yi は、AI を理解するための 2 つの基本原則、倹約と自己一貫性を提案しました。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

