Python で接続線のある二重円グラフを描画する方法

1. 必要なライブラリをインポートします

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import ConnectionPatch
from matplotlib import cm

matplotlib.patches モジュールの ConnectionPatch クラスを使用して、2 つのサブプロット間の接続を描画できます。二重円グラフなどのビジュアライゼーションでは、このクラスを使用して 2 つのサブグラフ間の接続を描画し、サブグラフ間の関係を表現できます。このクラスは、接続のスタイルや位置などのプロパティを制御するために使用できる多くのパラメーターとメソッドを提供します。

ConnectionPatch は、Matplotlib に接続を追加するために使用されます。その主なパラメータは次のとおりです:

• xyA: 接続線の開始点;

• xyB: 接続線の終点;

• coordsA: 始点の座標系、デフォルトはデータ;

• coordsB: 終了点の座標系、デフォルトはデータ;

• axesA: 開始点が位置する Axes オブジェクト;

• axesB: 終点が配置されている Axes オブジェクト ;

• color: 接続線の色;

• linewidth: 接続線の線の幅;

• linestyle: 接続線の線のスタイル。

ConnectionPatch の一般的に使用されるメソッドは次のとおりです:

• set_color: 接続線の色を設定します。

• set_linewidth: 接続線の線幅を設定します;

• set_linestyle: 線のスタイルを設定します接続線の。

cm は Matplotlib のカラー マッピング モジュールで、単一トーン、セグメント化されたカラーリング、連続グラデーション カラーリングなどを含む一連のカラー スキームを提供し、ユーザーのニーズをよりよく満たすことができます。データの視覚化。

2. データの準備

# 大饼图数据
labels = ['301', '302', '303', '304', '305', '307', '308', '306']
size = [219324, 94739, 75146, 71831, 54051, 21458, 9990, 50843]
# 大饼图分裂距离
explode = (0, 0, 0, 0, 0, 0, 0, 0.1)
# 小饼图数据
labels2 = ['402', '407']
size2 = [12255, 207069]
width = 0.2

このコードは、大きな円グラフと小さな円グラフのデータを定義し、大きな円グラフの分割距離と幅を設定するために使用されます。小さな円グラフ。

具体的な説明は次のとおりです。

• labels: 円グラフの各分割ブロックのラベル、つまり、どの領域を表すかを定義します。

• size: 円グラフの各分割ブロックのサイズを定義します。これは、各領域の数または割合を意味します。

• explode: 大きな円グラフの各分割ブロックと円の中心の間の距離、つまり、分割ブロックをポップアップする必要があるかどうかを定義します。ポップアップしません。

• labels2: 小さな円グラフの各分割ブロックのラベル、つまり、どの領域を表すかを定義します。

• size2: 小さな円グラフの各分割ブロックのサイズを定義します。これは、各領域の数または割合を意味します。

• width: 小さな円グラフの幅を定義します。ここでは 0.2 に設定します。

3. 二重円グラフを描画する

3.1 キャンバス オブジェクトとサブグラフ オブジェクトを作成する

fig = plt.figure(figsize=(9, 5))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)

コードのこの部分では、サイズ (9, 5) が作成されます。 ) キャンバス図、およびキャンバス上に 2 つのサブ図 ax1 と ax2 を追加しました。

このうち、

fig.add_subplot(121) は、キャンバスを 1 行 2 列のサブプロットに分割し、最初のサブプロット (つまり、左側のサブプロット) を選択することを意味します。 #fig .add_subplot(122) は、2 番目のサブプロット (つまり、右側のサブプロット) を選択することを意味します。サブグラフの番号付けルールは配列インデックスと似ています。行番号は上から下に 1 から増加し、列番号は左から右に 1 から増加します。たとえば、(1, 1) は最初のサブグラフを表します行と最初の列、( 1, 2) は、最初の行と 2 列目の部分グラフを表します。ここで、121 と 122 は、それぞれ最初の行の最初と 2 番目のサブグラフを表します。 3.2 大きな円グラフの描画

ax1.pie(size,
        autopct='%1.1f%%',
        startangle=30,
        labels=labels,
        colors=cm.Blues(range(10, 300, 50)),
        explode=explode)

このコードは、最初のサブグラフ (ax1) に円グラフを描画するために使用されます。特定のパラメータの意味は次のとおりです。

size: 円グラフ データ。各円グラフ ブロックのサイズを示します。
autopct: 円グラフ ブロックのデータ ラベル形式 "%1.1f%%" は、小数点以下 1 桁を保持し、パーセント記号を追加することを意味します。
startangle: 円グラフ ブロックの開始角度。30 度が開始点で、時計回りに回転します。
labels: サイズに対応する円グラフ ブロックのラベル。
colors: 円グラフ ブロックの色。cm.Blues() 関数を使用してカラー リストを生成します。
explode: 円グラフ ブロックの分割距離。円グラフの中心から離れているかどうかを示します。たとえば、(0, 0, 0, 0, 0, 0, 0, 0.1) は、最後のパイ片が中心から 0.1 半径離れていることを意味します。
これらのパラメータや円グラフの他のパラメータを必要に応じて調整して、目的の効果を得ることができます。

3.3 小さな円グラフの描画

ax2.pie(size2,
        autopct='%1.1f%%',
        startangle=90,
        labels=labels2,
        colors=cm.Blues(range(10, 300, 50)),
        radius=0.5,
        shadow=False)

このコードは、2 番目の小さな円グラフを描画するために使用されます。パラメータの具体的な意味は次のとおりです:

size2: 小さな円グラフのデータ、つまり [12255, 207069];
autopct: くさび形の書式設定 ブロックのデータ ラベル ‘%1.1f%%’ は、小数点以下 1 桁を保持し、その後にパーセント記号を追加することを意味します;

• startangle: 開始角度小さな円グラフの角度 (度で表されます)、ここでは 90 度、つまり垂直方向から開始するように設定されています;

• labels2: 小さな円グラフのラベル、つまり、 [‘402’, ‘407’] ;

• colors: 色を指定します。ここでは cm.Blues 関数を使用して青系の色のセットを生成します。

• #radius: 小さな円グラフの半径、ここでは 0.5 に設定;

• shadow: 影を追加するかどうか、ここでは False に設定します。

在这段代码中，我们创建了一个名为 ax2 的子区域对象，并使用 pie 方法绘制了一个小饼图，将 size2 中的数据作为输入数据。其他参数指定了锲形块的格式、颜色、标签等属性，进一步定制了图形的样式。

3.4 连接线1，连接大饼图的上边缘和小饼图的饼块

theta1, theta2 = ax1.patches[-1].theta1, ax1.patches[-1].theta2
center, r = ax1.patches[-1].center, ax1.patches[-1].r
x = r * np.cos(np.pi / 180 * theta2) + center[0]
y = np.sin(np.pi / 180 * theta2) + center[1]
con1 = ConnectionPatch(xyA=(0, 0.5),
                       xyB=(x, y),
                       coordsA=ax2.transData,
                       coordsB=ax1.transData,
                       axesA=ax2, axesB=ax1)

这部分代码是用来计算连接两个饼图的连接线的起点和终点位置，并创建一个 ConnectionPatch 对象用于绘制连接线。

• theta1 和 theta2 分别表示饼图上最后一个扇形的起始角度和终止角度。

• center 表示饼图中最后一个扇形的中心点位置。

• r 表示饼图的半径。

• x 和 y 表示连接线的终点坐标，其中 x 通过利用三角函数计算出来。

接下来，ConnectionPatch 的参数解释：

• xyA 表示连接线的起点位置，这里设为 (0, 0.5) 表示在小饼图上以它的左边中间位置为起点。

• xyB 表示连接线的终点位置，这里为 (x, y) 表示在大饼图上以计算得到的 x 和 y 为终点位置。

• coordsA 和 coordsB 表示起点和终点所在的坐标系，这里分别为小饼图和大饼图的坐标系。

• axesA 和 axesB 分别表示起点和终点所在的子图对象，这里分别为小饼图和大饼图的子图对象，即 ax2 和 ax1。

3.5 连接线2，连接大饼图的下边缘和小饼图的饼块

x = r * np.cos(np.pi / 180 * theta1) + center[0]
y = np.sin(np.pi / 180 * theta1) + center[1]
con2 = ConnectionPatch(xyA=(-0.1, -0.49),
                       xyB=(x, y),
                       coordsA='data',
                       coordsB='data',
                       axesA=ax2, axesB=ax1)

这段代码用于创建连接线的第二个对象con2。具体解释如下：

• x 和 y 分别代表了连接线从小饼图中(-0.1,-0.49)这个点出发，到大饼图中theta1角度对应的点的终点坐标。其中，theta1是通过访问ax1.patches[-1].theta1获得的。

• coordsA 和 coordsB 表示终点和起点坐标的坐标系类型。这里都是 ‘data’ 表示使用数据坐标系，即默认的 x 和 y 坐标值。

• axesA 和 axesB 表示终点和起点所在的子图对象。其中，axesA 为小饼图，axesB 为大饼图。

• 这里使用ConnectionPatch函数创建连接线对象。

3.6 添加连接线

for con in [con1, con2]:
    con.set_color('gray')
    ax2.add_artist(con)
    con.set_linewidth(1)

这段代码用于设置连接线的颜色和粗细，并将连接线添加到小饼图的坐标系上。具体来说，循环遍历连接线对象列表 [con1, con2]，并依次对每个连接线进行以下操作：

• 调用 set_color() 方法设置连接线的颜色为灰色。

• 调用 ax2.add_artist() 方法将连接线添加到小饼图的坐标系上。

• 调用 set_linewidth() 方法设置连接线的宽度为 1。

3.7 调整子图布局

fig.subplots_adjust(wspace=0)
plt.show()

这行代码调整了子图之间的水平间距，将间距设置为0，即将子图紧密排列。wspace参数表示子图之间的宽度间距。具体来说，这行代码将第一个子图和第二个子图之间的间距设置为0，使它们之间没有空隙。

四、源代码

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import ConnectionPatch
from matplotlib import cm
# 大饼图数据
labels = ['301', '302', '303', '304', '305', '307', '308', '306']
size = [219324, 94739, 75146, 71831, 54051, 21458, 9990, 50843]
# 大饼图分裂距离
explode = (0, 0, 0, 0, 0, 0, 0, 0.1)
# 小饼图数据
labels2 = ['402', '407']
size2 = [12255, 207069]
width = 0.2
# 创建画布和子图对象
fig = plt.figure(figsize=(9, 5))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
# 绘制大饼图
ax1.pie(size,
        autopct='%1.1f%%',
        startangle=30,
        labels=labels,
        colors=cm.Blues(range(10, 300, 50)),
        explode=explode)
# 绘制小饼图
ax2.pie(size2,
        autopct='%1.1f%%',
        startangle=90,
        labels=labels2,
        colors=cm.Blues(range(10, 300, 50)),
        radius=0.5,
        shadow=False)
# 连接线1，连接大饼图的上边缘和小饼图的饼块
theta1, theta2 = ax1.patches[-1].theta1, ax1.patches[-1].theta2
center, r = ax1.patches[-1].center, ax1.patches[-1].r
x = r * np.cos(np.pi / 180 * theta2) + center[0]
y = np.sin(np.pi / 180 * theta2) + center[1]
con1 = ConnectionPatch(xyA=(0, 0.5),
                       xyB=(x, y),
                       coordsA=ax2.transData,
                       coordsB=ax1.transData,
                       axesA=ax2, axesB=ax1)
# 连接线2，连接大饼图的下边缘和小饼图的饼块
x = r * np.cos(np.pi / 180 * theta1) + center[0]
y = np.sin(np.pi / 180 * theta1) + center[1]
con2 = ConnectionPatch(xyA=(-0.1, -0.49),
                       xyB=(x, y),
                       coordsA='data',
                       coordsB='data',
                       axesA=ax2, axesB=ax1)
# 添加连接线
for con in [con1, con2]:
    con.set_color('gray')
    ax2.add_artist(con)
    con.set_linewidth(1)
# 调整子图布局
fig.subplots_adjust(wspace=0)
# 显示图像
plt.show()

可视化结果为：

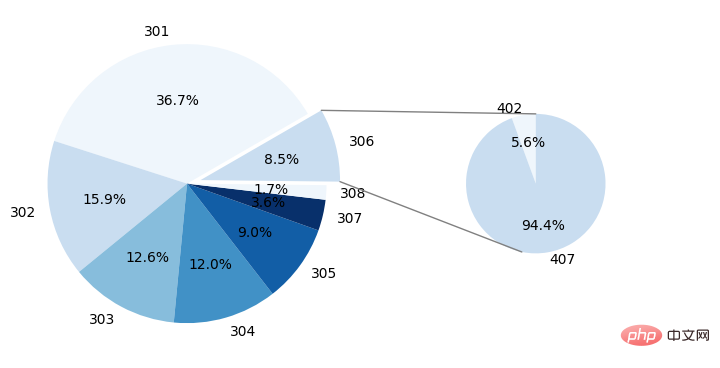
以上がPython で接続線のある二重円グラフを描画する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。