Python を使用して行列のノルムと行列式を見つける方法

scipy.linalg の関数ではパラメータが 2 つ指定されることが多く、1 つは check_finite で、True の場合は限定的なチェックが行われます。もう 1 つのタイプは overwrite_xxxx で、計算プロセス中に xxxxx を上書きできるかどうかを示します。簡単にするために、a は上書きスイッチを提供することを後で説明しますが、これはパラメーター overwrite_a があることを意味します。これが True の場合、a は計算プロセス中に上書きできます。制限付きチェック スイッチが提供されている場合は、check_finite パラメーターが提供されていることを意味します。

Norm

関数

norm は、

norm(a, ord=None, axis=None, keepdims=False, check_finite=True)

## として定義されるノルムを見つけるために scipy.linalg に提供されています #ここで、

ord

は、ノルム

##ord行列ノルムベクトルノルム ## の次数を宣言するために使用されます。 ##なしフロベニウス ノルム2-ノルムフロベニウス ノルム核規範##-##max(sum(abs(a), axis=1))#-infmin ⁡ ( ∣ a ∣ ) 0-1max(sum(abs(a), axis=0))##-1min(sum(abs(a), axis=0))2最小特異値a がベクトル、 ordフロベニウス ノルムは次のように定義できます。

		'fro'
##-	##「nuc」
##inf		max ⁡ ( ∣ a ∣ )
	min(sum(abs(a), axis=1))
	##sum(a!= 0)
2 -ノルム (最大特異値)		-2
がゼロ以外の整数の場合、n nn として記録されます。 a i a_iai を要素とします。行列 a aa の場合、行列の n nn ノルムは		核ノルム この数値は「トレース ノルム」とも呼ばれ、すべての特異値の合計を表しますマトリックスの。

本質は、行列内のベクトルの 2 ノルムの自然な一般化です。

scipy.linalg

に加えて、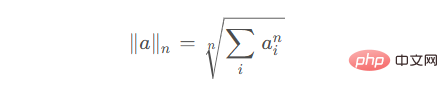norm

も

numpy.linalg

で提供され、そのパラメータは

norm(x, ord=None, axis=None, keepdims=False)

## です

#order

のオプションのパラメーターは、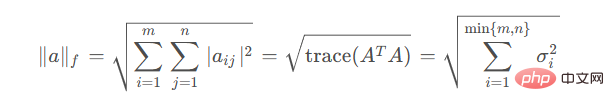scipy.linalg

の

norm

関数と同じです。

行列式scipy.linalgでは、行列式関数はdet

であり、その定義は、見つける行列を除けば非常に簡単です。

a 以外には、オーバーライド スイッチと a の限定的なチェックのみがあります。 例は次のとおりです。

import numpy as np
from scipy import linalg
a = np.array([[1,2,3], [4,5,6], [7,8,9]])
linalg.det(a)
# 0.0
a = np.array([[0,2,3], [4,5,6], [7,8,9]])
linalg.det(a)
# 3.0

trace

scipy.linalg は trace 関数を提供しませんが、numpy 提供される場合、

umpy.trace(a, offset=0, axis1=0, axis2=1, dtype=None, out=None)

として定義されます。ここで、

offset

はオフセットであり、主対角線に対する相対的なオフセットを示します。

axis1、axis2 は座標軸を表します

#dtype
• 調整に使用されるデータ型出力値

  >>> x = np.random.rand(3,3)
  >>> print(x)
  [[0.26832187 0.64615363 0.09006217]
   [0.63106319 0.65573765 0.35842304]
   [0.66629322 0.16999836 0.92357658]]
  >>> np.trace(x)
  1.8476361016546932

以上がPython を使用して行列のノルムと行列式を見つける方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。