ホームページ >Java >&#&チュートリアル >Java 開発ではどのような一般的なアルゴリズムがよく使用されますか?
Java 開発ではどのような一般的なアルゴリズムがよく使用されますか?
- 王林転載
- 2023-05-09 10:04:151727ブラウズ
貪欲なアルゴリズム
古典的なアプリケーション: ハフマン符号化、プリムおよびクラスカルの最小スパニング ツリー アルゴリズム、ダイクストラの単一ソース最短パス アルゴリズムなど。
問題を解決するための貪欲なアルゴリズムのステップ
最初のステップとして、この種の問題が発生した場合は、まず貪欲なアルゴリズムについて考える必要があります。データのセットに対して、限界値と期待値を定義し、いくつかのデータを選択することを望みます。値を制限した場合、期待値が最も大きくなります。
先ほどの例から類推すると、制限値は重量が 100kg を超えることはできず、期待値はアイテムの合計値です。このデータセットは5種類の豆です。その中から重さが100kg以下で合計価値が最も高い部分を選びます。
2 番目のステップでは、貪欲なアルゴリズムでこの問題を解決できるかどうかを確認します。毎回、現在の状況で期待値に最も寄与し、期待値にも同量寄与するデータを選択します。限界値。
先ほどの例と同様に、毎回残りの豆の中から最も単価の高い豆、つまり 同じ重量##の場合に最も価値に貢献する豆を選択します。 #。
3 番目のステップでは、貪欲アルゴリズムによって生成された結果が最適かどうかを確認するために、いくつかの例を示します。ほとんどの場合、確認のために例をいくつか挙げるだけで済みます。貪欲アルゴリズムの正しさを厳密に証明することは非常に複雑であり、多くの数学的推論を必要とします。 貪欲アルゴリズムが機能しない主な理由は、前の選択が後の選択に影響を与えることです。貪欲なアルゴリズムの実践的な分析
1. キャンディーをシェアする 私たちには m 人のキャンディーと n 人の子供がいます。ここで、これらの子供たちにキャンディーを配布したいと考えていますが、キャンディーの数が少なく、子供たちの数が多いため (m
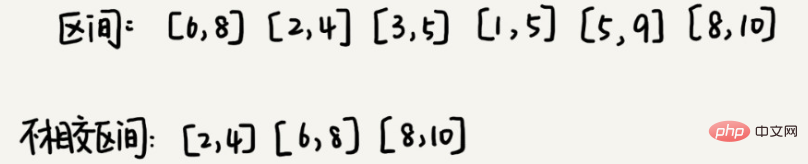
貪欲アルゴリズムを使用してハフマン コーディングを実装するにはどうすればよいですか?
ハフマン符号化では、この不等長符号化方式を使用して文字を符号化します。 各文字のエンコーディング間では、あるエンコーディングが別のエンコーディングのプレフィックスになる状況が存在しないことが必要です。 頻繁に出現する文字には少し短いエンコーディングを使用し、あまり出現しない文字には少し長いエンコーディングを使用します。
1000 文字を含むファイルがあるとします。各文字は 1 バイト (1 バイト = 8 ビット) を占めます。これらの 1000 文字を保存するには合計 8000 ビットが必要です。もっとスペースを節約できる保存方法はありますか?
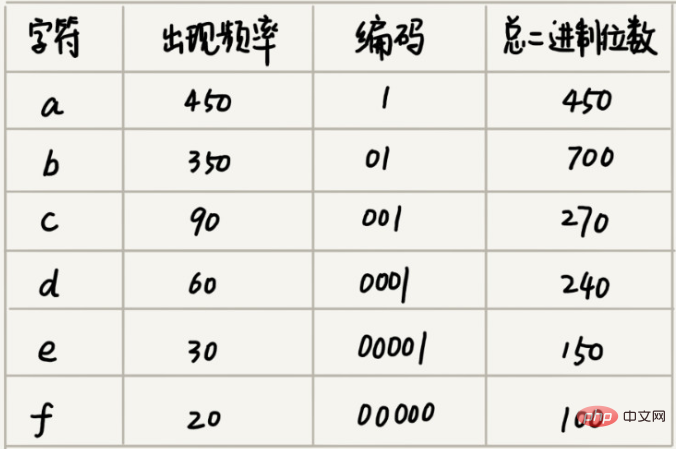
統計分析により、これらの 1000 文字には 6 つの異なる文字しか含まれていないことが判明したとします (a、b、c、d、e、f とする)。 3 つのバイナリ ビットで 8 つの異なる文字を表すことができるため、記憶領域を最小限に抑えるために、各文字を表すのに 3 つのバイナリ ビットを使用します。この 1,000 文字を保存するには 3,000 ビットしか必要とせず、元の保存方法よりも多くのスペースを節約できます。しかし、もっと省スペースな保管方法はあるのでしょうか?
a(000)、b(001)、c(010)、d(011)、e(100)、f(101)
ハフマン符号化は非常に効率的な符号化方式であり、データ圧縮に広く使用されており、その圧縮率は通常 20% ~ 90% です。
ハフマン符号化では、テキスト中に異なる文字が何個あるかを調べるだけでなく、各文字の頻度も調べ、その頻度に基づいて、異なる長さのコードを選択します。ハフマン符号化では、この不等長符号化方式を利用して圧縮効率をさらに高めようとしています。頻度が異なる文字に対して異なる長さのコードを選択するにはどうすればよいですか?欲張りに考えると、出現頻度の高い文字には少し短いコードを使用し、出現頻度の低い文字には少し長いコードを使用できます。
コードの長さが同じではありません。コードを読み取って解析するにはどうすればよいですか?
等長エンコードの場合、解凍するのは非常に簡単です。たとえば、先ほどの例では、文字を表すために 3 ビットを使用します。解凍時には、毎回テキストから 3 桁のバイナリ コードを読み取り、対応する文字に変換します。しかし、ハフマン符号は同じ長さではなく、毎回 1 ビットを読み取るべきでしょうか、それとも伸長の際に 2 ビット、3 ビットなどを読み取るべきでしょうか?この問題により、ハフマン コーディングの解凍がより複雑になります。解凍プロセス中のあいまいさを避けるために、ハフマン エンコーディングでは、各文字のエンコーディング間で、あるエンコーディングが別のエンコーディングのプレフィックスになる状況が存在しないことが必要です。
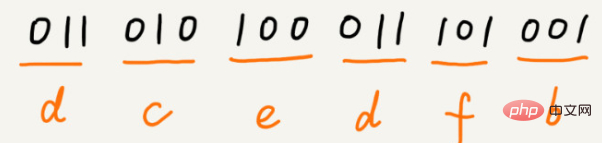
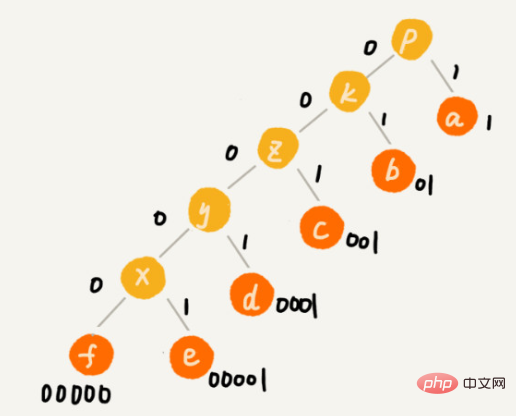
これら 6 つの文字の頻度が高いものから低いものまで、a、b、c、d、e、f であるとします。このようにエンコードします。どの文字のエンコードも別の文字のプレフィックスではありません。解凍するときは、毎回できるだけ長い解凍可能なバイナリ文字列を読み取るため、あいまいさが生じません。このエンコードと圧縮の後、これらの 1000 文字に必要なのは 2100 ビットだけです。
ハフマン符号化の考え方は理解するのが難しくありませんが、文字の出現頻度に応じて異なる長さの異なる文字を符号化するにはどうすればよいでしょうか?
大きなトップパイルを使用し、頻度に従ってキャラクターを配置します。
分割統治アルゴリズム
分割統治アルゴリズムの核となる考え方は、実際には 4 つの単語です。分割統治、つまり、元の問題を、元の問題と同様の構造を持つ n 個の小さなサブ問題に分割し、再帰的に分割します。これらの部分問題を解決し、その結果を組み合わせると、元の問題の解決策が得られます。
分割統治アルゴリズムは問題解決のアイデアであり、再帰はプログラミング手法です。実際、分割統治アルゴリズムは一般に再帰を使用して実装するのがより適しています。分割統治アルゴリズムの再帰的実装では、再帰の各レベルに次の 3 つの操作が含まれます。
分解: 元の問題を一連のサブ問題に分解します;
解決策: 各サブ問題を再帰的に解決します。 -問題が十分に小さい場合、直接解決法;
マージ: サブ問題の結果を元の問題にマージします。
分割統治アルゴリズムで解決できる問題は、通常、次の条件を満たす必要があります。
元の問題は、分解された小さな問題と同じパターンを持っています。
元の問題は、次のようなサブ問題に分解されます。
には分解終了条件があり、問題が十分に小さい場合には、相関関係はありません。直接解決できる;
に分割できる 問題は元の問題にマージされ、このマージ操作の複雑さが高すぎてはいけません。アルゴリズム全体の複雑さを軽減します。
分割統治アルゴリズムの適用例の分析
データセットの順序ペアまたは逆ペアの数を見つけるようにプログラムするにはどうすればよいですか?
各数値とその後の数値を比較して、その数値より小さい数値がいくつあるかを確認します。それより小さい数の数を k として記録し、このように各数を調べた後、各数に対応する k の値を合計し、最終的に得られた合計が逆順のペアの数になります。ただし、この操作の時間計算量は O(n^2) です。
配列を A1 と A2 の 2 つの半分に分割し、A1 と A2 の逆順ペア K1 と K2 の数をそれぞれ計算し、次に A1 と A2 の間の逆順ペア K3 の数を計算します。 A2.この場合、配列 A の逆順ペアの数は K1 K2 K3 に等しくなります。 マージソートアルゴリズムの助けを借りて
10GB の注文ファイルを量に応じて分類する必要がありますか?
最初に注文をスキャンし、注文の量に基づいて 10 GB のファイルをいくつかの量の範囲に分割できます。たとえば、1 ~ 100 元の注文金額は小さなファイルに配置され、101 ~ 200 元の注文金額は別のファイルに配置されます。このようにして、各小さなファイルを個別に並べ替えるためにメモリにロードすることができ、最終的にこれらの順序付けされた小さなファイルがマージされて、最終的に順序付けされた 10 GB の順序データが形成されます。
バックトラッキングアルゴリズム
アプリケーション シナリオ: 深さ優先検索、正規表現一致、コンパイル原則における構文分析。数独、8 つのクイーン、0 ~ 1 のナップザック、グラフの色分け、巡回セールスマン問題、総順列など、多くの古典的な数学問題はバックトラッキング アルゴリズムを使用して解決できます。
バックトラックの処理の考え方は、列挙型検索に似ています。すべてのソリューションを列挙し、期待を満たすものを見つけます。考えられるすべての解決策を定期的に列挙し、漏れや重複を避けるために、問題解決のプロセスを複数の段階に分割します。各段階で、私たちは道の分岐点に直面します。最初にランダムに道を選択します。この道が機能しない(期待される解決策を満たさない)ことがわかったら、前の分岐点に戻り、別の道を選んで歩き続けてください。
8 クイーンズ問題
8x8 のチェス盤があり、その上に 8 つのチェスの駒 (クイーン) を配置したいと考えています。各チェスの駒の行、列、または対角に別のチェスの駒を配置することはできません。
1.0-1 バックパック
多くのシナリオをこの問題モデルに抽象化できます。この問題に対する古典的な解決策は動的プログラミングですが、シンプルではありますが効率の低い解決策もあります。それが、今日説明するバックトラッキング アルゴリズムです。
私たちはバックパックを持っていますが、バックパックの総積載重量は Wkg です。これで n 個の項目があり、それぞれの重みが異なり、分割できません。次に、いくつかのアイテムを選択してバックパックにロードしたいと思います。バックパックが運ぶことができる重量を超えずに、バックパック内のアイテムの総重量を最大化するにはどうすればよいですか?
各アイテムには、バックパックに入れるか入れないかの 2 つの選択肢があります。 n 個の取り付け方法は 2^n 通りあり、総重量が Wkg を超えるものを除き、残りの取り付け方法から総重量が Wkg に最も近いものを選択します。しかし、これらの 2^n 個のふりを繰り返す方法を網羅的に列挙するにはどうすればよいでしょうか?
バックトラック法: 項目を順番に並べると、問題全体が n 段階に分解され、各段階が項目の選び方に対応します。最初に最初の項目を処理し、それをロードするかどうかを選択してから、残りの項目を再帰的に処理します。
動的プログラミング
動的プログラミングは、最大値や最小値を見つけるなど、最適な問題を解決するのに適しています。これにより、時間の複雑さが大幅に軽減され、コードの実行効率が向上します。
0-1 バックパックの問題
分割できない重さの異なるアイテムの場合、バックパックに入れるアイテムを選択する必要がありますが、バックパックの最大重量制限を満たすことを前提として、その中のアイテムの最大総重量はいくらになりますか?バックパックは? ######考え:
(1) 解決プロセス全体を n 段階に分割し、各段階でバックパックにアイテムを入れるかどうかを決定します。それぞれのアイテム(バックパックに入れるか入れないか)を決定すると、バックパック内のアイテムの重さはさまざまな状況、つまりさまざまな状態になります。これらは再帰ツリーに対応します。つまり、多くの異なるノードがあります。
(2) 各層の繰り返し状態 (ノード) をマージし、異なる状態のみを記録し、前の層の状態セットに基づいて次の層の状態セットを導出します。各層の繰り返しの状態をマージして、各層の異なる状態の数が w (w はバックパックの積載重量を表します) (この例では 9) を超えないようにすることができます。
n ステージに分割します。各ステージは前のステージに基づいて導出され、計算の繰り返しを避けるために動的に前進します。
バックトラッキング アルゴリズムを使用してこの問題を解決する場合の時間計算量は O(2^n) であり、指数関数的です。それでは、動的プログラミング ソリューションの時間計算量はどれくらいでしょうか?
最も時間がかかる部分はコード内の 2 層の for ループであるため、
時間計算量は O(n*w) です。 n はアイテムの数を表し、w はバックパックが運ぶことができる総重量を表します。 n 倍 w 1 の追加の 2 次元配列を適用する必要がありますが、これは多くのスペースを消費します。したがって、動的計画法は空間と時間を交換するソリューションであると言うこともあります。
0-1 バックパックのアップグレード版の問題
異なる重さ、異なる価値を持つ分割できないアイテムのセットとして、特定のアイテムをバックパックに入れることにします。バックパックの最大重量制限を満たすことを前提として、入れられるアイテムの合計値バックパックに入れるのが一番大きいのですが、いくらくらいですか?
動的計画法で解くのに適しているのはどのような問題ですか?
モデルの 3 つの特徴
Aモデル:多段階意思決定最適解モデル
3 つの特徴:
最適な部分構造、問題の最適な解決策には、部分問題の最適な解決策が含まれます 後遺症がない、最初のレベルの意味はい、後のステージの状態を導出するときは、前のステージの状態値のみを考慮し、この状態が段階的にどのように導出されるかには考慮しません。 2 つ目の意味は、ある段階のステータスが決定されると、その後の段階の決定には影響されないということです。 (後者は前者に影響しません。) 繰り返されるサブ問題、異なる決定シーケンスは、特定の同じ段階に到達すると、繰り返しの状態を生成する可能性があります。 動的プログラミングの問題解決に関する 2 つのアイデアのまとめ
1. 状態遷移表の作成方法
一般に、動的計画法で解決できる問題は、バックトラッキング アルゴリズムを使用した総当たり検索で解決できます。再帰ツリーを描画します。再帰ツリーから、繰り返される部分問題があるかどうか、および繰り返される部分問題がどのように生成されるかを簡単に確認できます。
重複した副問題を見つけた後、それに対処する方法は 2 つあります。1 つ目は、バックトラッキングを直接使用し、「メモ」 を追加して副問題の重複を避けることです。実行効率という点では、動的計画法の解決策の考え方と変わりません。 2 つ目の方法は、動的プログラミングである 状態遷移表法 を使用する方法です。
まず状態テーブルを描いてみましょう。状態テーブルは通常 2 次元であるため、2 次元配列と考えることができます。その中で、各状態には 3 つの変数、行、列、配列値が含まれています。意思決定プロセスに従って、前から後ろへ、そして再帰的な関係に従って、状態テーブルの各状態を段階的に埋めていきます。最後に、この再帰的なフォーム入力プロセスをコード (動的プログラミング コード) に変換します。
それを表現するために多くの変数が必要な場合、対応する状態テーブルは 3 次元や 4 次元などの高次元になる可能性があります。現時点では、状態遷移表手法を使用してそれを解決することは適していません。それは、一方では高次元の状態遷移表を描いて表現するのが難しいためであり、他方では、人間の脳は高次元のことを考えるのが本当に苦手だからです。
2. 状態遷移方程式の手法
私たちは、部分問題、いわゆる最適な部分構造を通じて特定の問題を再帰的にどのように解決できるかを分析する必要があります。最適な部分構造に基づいて、いわゆる状態遷移方程式である再帰式を書きます。状態遷移方程式を使用すると、コードの実装は非常に簡単になります。一般的に、コード実装方法は 2 つあります。1 つは 再帰と「メモ」 で、もう 1 つは 反復再帰 です。
min_dist(i, j) = w[i][j] min(min_dist(i, j-1), min_dist(i-1, j))
すべての問題が両方の問題解決アイデアに適しているわけではないことを強調したいと思います。 1 番目の考え方でより明確になる問題もあれば、2 番目の考え方でより明確になる問題もあるため、どの問題解決方法を使用するかは、具体的な問題を考慮して決定する必要があります。 状態遷移テーブル法問題解決のアイデアを大まかに要約すると、バックトラッキング アルゴリズムの実装 - 状態の定義 - 再帰ツリーの描画 - 繰り返される部分問題の検出 - 状態の描画遷移テーブル - 再帰に従ってプッシュ関係のフォーム入力 - フォーム入力プロセスをコード に変換します。 状態遷移方程式手法の一般的な考え方は次のように要約できます。 最適な部分構造を見つける - 状態遷移方程式を書く - 状態遷移方程式をコードに変換する。
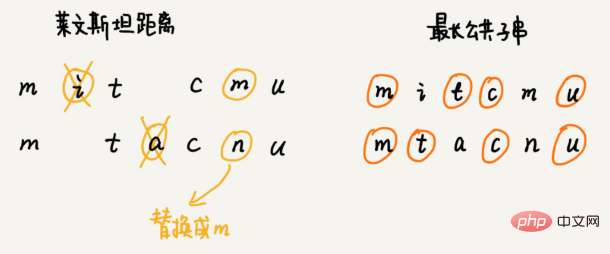
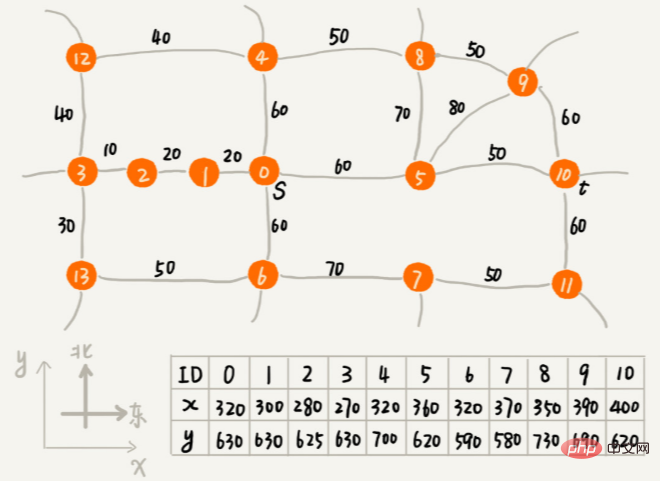
2 つの文字列の類似性を定量化するにはどうすればよいですか? 編集距離 は、ある文字列を別の文字列に変換するために必要な編集操作の最小数を指します (文字の追加、文字の削除、文字の置換など)。編集距離が大きいほど 2 つの文字列間の類似性は小さくなり、逆に、編集距離が小さいほど 2 つの文字列間の類似性は大きくなります。 2 つの同一の文字列の場合、編集距離は 0 です。 編集距離にはさまざまな計算方法がありますが、最も有名なものは、レーベンシュタイン距離 (レーベンシュタイン距離) と 最長共通部分文字列長 (最長共通部分文字列長) です。 。このうち、レビンシュタイン距離では、文字の追加、削除、置換の 3 つの編集操作が可能ですが、最長共通部分文字列の長さでは、文字の追加と削除の 2 つの編集操作のみが可能です。 レーベンシュタイン距離と最長共通部分文字列長は、まったく反対の 2 つの観点から文字列の類似性を分析します。レーベンシュタイン距離のサイズは 2 つの文字列間の差異を表し、最長の共通部分文字列のサイズは 2 つの文字列間の類似性を表します。 2 つの文字列 mitcmu と mtacnu のレビンシュタイン距離は 3 で、最も長い共通部分文字列の長さは 4 です。 レーベンシュタイン距離をプログラムで計算するにはどうすればよいですか? この問題は、ある文字列を別の文字列に変更するために必要な編集の最小回数を見つけることです。解決プロセス全体には複数の意思決定段階が含まれており、文字列内の各文字が別の文字列内の文字と一致するかどうか、一致した場合はどのように対処するか、一致しない場合はどのように対処するかを順番に検査する必要があります。 。したがって、この問題は 多段階意思決定最適解モデル に準拠します。 推奨アルゴリズム ベクトルの距離を使用して類似性を見つけます。 検索: A* 検索アルゴリズムを使用してゲームに経路探索機能を実装するにはどうすればよいですか? では、最短ルートに近い準最適ルートを素早く見つけるにはどうすればよいでしょうか? この高速パス プランニング アルゴリズムは、今日学習する A* アルゴリズムです。実際、A* アルゴリズムは、ダイクストラのアルゴリズムを最適化および変換したものです。 頂点と終点の間の直線距離、つまりユークリッド距離を使用して、頂点と終点の間の経路長を概算します (注: 経路長と直線距離) この距離は h(i) と記録されます (i はこの頂点の番号を表します) 専門名はヒューリスティック関数 (heuristic function) ユークリッド距離のため 計算式には時間のかかるルート計算が含まれるため、通常は別のより単純な距離計算式、つまりマンハッタン距離 (マンハッタン距離) を使用します。 マンハッタン距離は 2 つの距離の間です。ポイント 水平座標と垂直座標の間の距離の合計。計算プロセスには加算、減算、符号ビット反転のみが含まれるため、ユークリッド距離よりも効率的です。 int hManhattan(Vertex v1, Vertex v2) { // Vertex は後で定義される頂点を表します
return Math.abs(v1.x - v2.x) Math.abs(v1.y - v2.y);
}
f(i)=g(i) h(i)、頂点と始点間の経路長 g(i)、頂点から終点までの推定経路長 h(i) . f(i) の専門名は評価関数です。 A* アルゴリズムは、ダイクストラのアルゴリズムを単純に修正したもので、最小の f(i) が最初にリストされます。 これとダイクストラのアルゴリズムのコード実装との間には、主に 3 つの違いがあります。 優先キューの構築方法が異なります。 A* アルゴリズムは f 値 (つまり、先ほど述べた f(i)=g(i) h(i)) に基づいて優先キューを構築しますが、ダイクストラ アルゴリズムは dist 値 (つまり、f(i)=g(i) h(i)) に基づいて優先キューを構築します。は、g( 先ほど述べた) i)) 優先キューを構築するためのものです; A* アルゴリズムは、頂点 dist 値を更新するときに f 値を同期的に更新します; ループの終了条件も異なります。ダイクストラ アルゴリズムはエンドポイントがデキューされると終了し、A* アルゴリズムはトラバーサルがエンドポイントに到達すると終了します。

以上がJava 開発ではどのような一般的なアルゴリズムがよく使用されますか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

