ホームページ >バックエンド開発 >Python チュートリアル >Python で凸包をプロットするにはどうすればよいですか?
Python で凸包をプロットするにはどうすればよいですか?
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB転載
- 2023-05-08 19:25:062098ブラウズ
ConvexHull
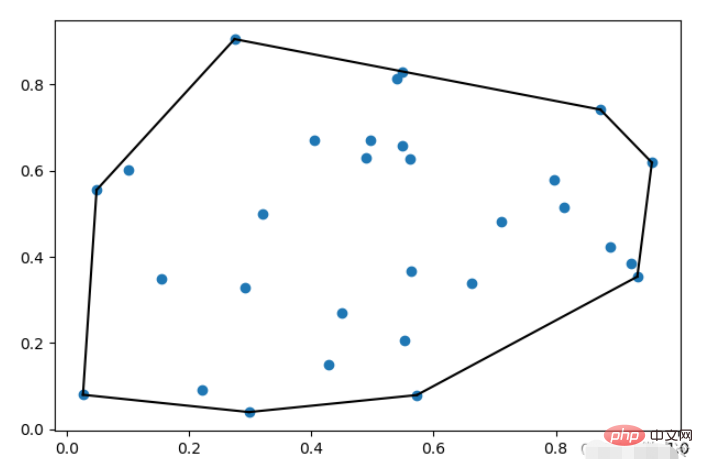
ConvexHull は空間クラスであり、その主な機能は、一連の点のエッジを見つけて凸包を作成することです。必要な初期化パラメータは点セットであり、点セットの形式はn×m次元の配列であり、nは点セット内の点の数、mは点の次元である。
from scipy.spatial import ConvexHull
import matplotlib.pyplot as plt
import numpy as np
pts = np.random.rand(30, 2)
hull = ConvexHull(pts)
plt.plot(pts[:,0], pts[:,1], 'o')
for i in hull.simplices:
plt.plot(pts[i, 0], pts[i, 1], 'k-')
plt.show()simplex はインデックス ポイントのシリアル番号です。描画後の効果は次のとおりです。
ConvexHull には 2 つのオプションのパラメータがありますこのうち、incremental はブール値パラメータで、True の場合、新しいポイントの追加が許可されます。
qhull_options の特定のパラメータは qhull で確認できますが、以下では QG のみを説明します。
QG
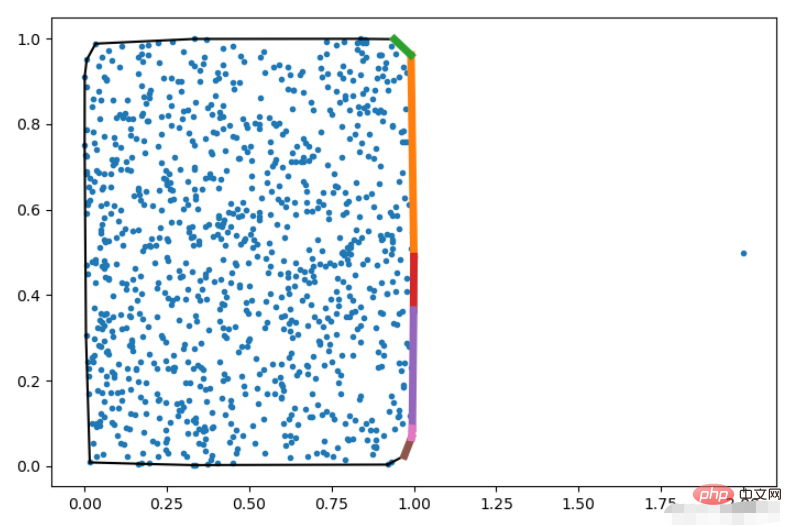
QGn は、n 番目の点を観測点として扱うことを意味します。点セットを凸包で分割した後、頂点を接続して壁として使用すると、観測点は次のようになります。見える点は良好とマークされ、その効果は次のとおりです。
pts = np.random.rand(1000, 2)
# 添加一个观察点
pts = np.vstack([pts, np.array([[2,0.5]])])
hull = ConvexHull(pts, qhull_options='QG1000')
plt.plot(pts[:,0], pts[:,1], '.')
for i in hull.simplices:
plt.plot(pts[i, 0], pts[i, 1], 'k-')
for i in hull.simplices[hull.good]:
plt.plot(pts[i, 0],pts[i, 1], lw=5)
plt.show()効果は図に示すとおりです。
3 次元の状況
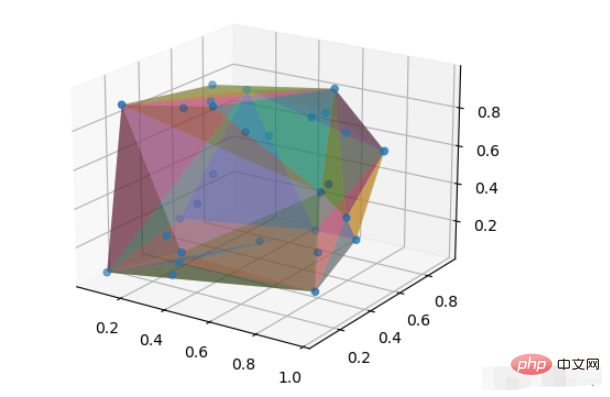
二次元の凸包は明らかに線で構成された閉じた図形ですが、三次元の凸包は当然三次元の幾何学であるはずです。任意の次元に拡張すると、凸包は実際には単体になります。ConvexHull の単体は単体を形成する点であり、原点セットでインデックス付けされます。例は次のとおりです。
pts = np.random.rand(30, 3)
hull = ConvexHull(pts)
ax = plt.subplot(projection='3d')
ax.scatter(pts[:,0], pts[:,1], pts[:,2])
for i in hull.simplices:
ax.plot_trisurf(pts[i, 0], pts[i, 1], pts[i,2], alpha=0.5)
plt.show()アルファ パラメータは、凸包の内側の点が凸包を通して見えるように、三角形の表面の透明度を調整するために使用されます。
効果は次のとおりです。
ConvexHull 属性
シンプレックスの概念は以前に導入されました。つまり、合成された図形です。凸包の は単体です。二次元の場合、凸包は線分で囲まれ、三次元の場合、凸包は平面で囲まれ、任意の次元に拡張すると、凸包を構成する単体として表現できます。超曲面によって。超曲面の概念には境界がないため、以下では頂点とエッジを持つ凸包曲面を単体超曲面と呼びます。
ConvexHull クラスで一般的に使用される属性は次のとおりです。
points 凸包で囲まれた点セット
vertices Simplex点の頂点 集中インデックス
simplice 単体メタサーフェス頂点
neighbors 超曲面隣接超曲面のインデックス
- # #equations 超曲面方程式のパラメーター
>>> hull.equations
array([[-0.5509472 , 0.72386104, -0.41530999, -0.36369123],
[-0.26155355, 0.16210178, -0.95147925, 0.02022163],
[-0.99132368, -0.0460725 , 0.12310441, 0.045523 ],
[-0.98526526, -0.07170442, 0.15527666, 0.04749854],
[-0.15900968, -0.98529789, -0.06248198, 0.13294496],
# .......以上がPython で凸包をプロットするにはどうすればよいですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

