ミクロビューのインセンティブと需要と供給のシナリオにおける因果推論の適用

#1. 因果推論とインセンティブ アルゴリズム

#1. ビジネスの背景とビジネス モデリング

まず、Tencent Weishi の紅包インセンティブ事業の背景を簡単にご紹介します。他の製品やシナリオと同様に、所定の予算内で、Tencent Weishi のユーザーに現金インセンティブを発行し、現金インセンティブを通じてユーザーの翌日の維持率と同日の使用時間を最大化することを目指しています。現金インセンティブの主な形式は、不定期にユーザーに不特定枚数および不特定金額の現金赤い封筒を発行することです。上記の 3 つの「不確実性」は、最終的にはアルゴリズムによって決定されます。この 3 つの「不確実性」は、赤封筒インセンティブ戦略の 3 要素とも呼ばれます。

# 次に、さまざまな現金インセンティブ戦略の抽象的な形式について説明します。最初のものは、赤いエンベロープ シーケンスの形式で戦略を表現します。たとえば、赤いエンベロープ シーケンスに番号を付け、次にワンホットの形式で各治療に独立して番号を付けます。その利点は、各赤い封筒と他の詳細な戦略の間の量、および対応する効果など、より詳細を描写できることです。しかし、これには必然的に戦略を表すためにより多くの変数が必要となり、戦略の探索空間は非常に大きくなり、戦略を探索して選択する際により多くの計算が必要になります。 2 番目の形式は、3 要素ベクトルを使用して戦略を表し、探索においてより柔軟で効率的ですが、一部の詳細は無視されます。 3 番目の方法はより数学的です。つまり、赤いエンベロープ シーケンスが時間 t に関する関数になり、関数内のパラメーターは戦略を表すベクトルを形成できます。因果関係の問題のモデル化と戦略の表現は、因果効果推定の精度と効率を大きく左右します。

適切な戦略の抽象化とベクトル表現があると仮定して、次に行うべきことは、アルゴリズム フレームワークを選択することです。ここには 3 つのフレームワークがあります。 最初の フレームワークは業界では比較的成熟しており、因果推論と多目的制約の最適化を組み合わせて戦略を割り当て、最適化します。このフレームワークでは、因果推論は主に、さまざまな戦略に対応するコアとなるユーザー指標、つまりユーザー維持率と継続時間の改善と呼ばれるものを推定する役割を果たします。推定後、多目的制約付き最適化を使用して、予算制約を満たすためのオフライン予算戦略割り当てを実行します。 2 番目のタイプは、多目的制約最適化手法と組み合わせたオフライン強化学習です。私は個人的に、この方法は主に 2 つの理由からより有望だと考えています。 1 つ目の理由は、実際のアプリケーション シナリオでは多くの戦略が存在し、強化学習自体が効率的に戦略空間を探索できること、同時に、戦略が依存しているため、強化学習は戦略間の依存関係をモデル化できることです。オフラインの強力な化学反応の本質は、実際には反事実推定の問題であり、それ自体が強い因果関係を持っているということです。残念ながら、私たちのシナリオではオフラインの強化学習方法を試しましたが、そのオンライン効果は期待した効果を達成できませんでした。その理由は、一方では手法の問題であり、他方では主にデータによって制限されるためです。優れたオフライン強化学習モデルをトレーニングするには、データ内の戦略分布が十分に広いか、戦略分布が十分に均一である必要があります。言い換えれば、ランダム データを使用するか観測データを使用するかに関係なく、できるだけ多くのそのような戦略を探索することを望んでおり、分布は比較的均等になるため、反事実の数を減らすことができます。最後のアルゴリズム フレームワークは、広告シナリオでは比較的成熟しており、オンライン強化学習を使用してトラフィックと予算を制御します。この方法の利点は、オンラインの緊急事態にタイムリーかつ迅速に対応できると同時に、より正確に予算を管理できることです。原因と結果の導入後、トラフィックの選択や制御に使用する指標は ECPM 指標ではなくなり、現在推定されている維持率と期間が改善される可能性があります。一連の実践的な試みの後、私たちは最終的に最初のアルゴリズム フレームワークを選択しました。これは、因果推論と多目的制約の最適化を組み合わせたものです。これは、より安定していて制御可能であり、オンライン エンジニアリングへの依存も少ないためです。

最初のアルゴリズム フレームワークのパイプラインを次の図に示します。まず、ユーザーの特性がオフラインで計算され、次に因果モデルを使用して、さまざまな戦略の下でのユーザーの中核指標の改善、いわゆるアップリフトが推定されます。推定された改善に基づいて、多目的最適化を使用して最適な戦略を解決し、割り当てます。プロセス全体の計算を高速化するために、構造化するときに事前に群衆をクラスター化します。これは、このクラスター内の人々が同じ原因と結果を持っていると信じて、それに応じて同じ戦略を割り当てることを意味します。同じクラスター内の人々。

#2. 戦略仮説と因果関係図

上記の議論を踏まえて、戦略を抽象化する方法に焦点を当てましょう。まず、因果関係図を抽象化する方法を見てみましょう。赤い封筒のインセンティブ シナリオでモデル化する必要がある原因と結果は、複数の日と複数の赤い封筒に反映されます。前の赤い封筒は次の赤い封筒が受信されるかどうかに確実に影響を与えるため、これは本質的に時間変動治療効果の問題であり、右に示すような時系列因果図に抽象化されます。

1 日に複数の赤い封筒を受け取った場合、T の下付き文字はすべて赤い封筒のシリアル番号を表します。このときのTは、現在の赤封筒の量と最後に赤封筒が発行されてからの時間間隔からなるベクトルを表します。 Y は、赤い封筒が発行されてからのユーザーの使用時間と、翌日のリテンションの増加です。 X は、ユーザーの視聴行動や人口統計的属性など、現時点までに観察された交絡変数です。もちろん、U で表される、ユーザーの時折の滞在や時折の停止など、観測されていない交絡変数が多数存在します。重要な観察されていない交絡変数はユーザーの心であり、これには主に赤い封筒のインセンティブの額に対するユーザーの価値評価が含まれます。これらのいわゆる心は、システム内の統計量や統計特性によって表現するのが困難です。

レッドエンベロープ戦略を時系列の形式でモデル化することは非常に複雑になるため、合理的な簡略化をいくつか行いました。たとえば、U は現時点では T、X、Y にのみ影響し、次の瞬間、つまりユーザーの心には U のみに影響を与えるとします。つまり、次の瞬間の価値評価や心理に影響を与えることで、将来のYに影響を与えるだけです。しかし、一連の単純化を行った後でも、時系列因果関係図全体が依然として非常に密であり、合理的な推定を行うことが困難であることがわかります。また、時間変動トレンド効果を解くために G 法を使用する場合、学習には大量のデータが必要ですが、実際には得られるデータが非常にまばらであるため、オンラインで良好な効果を得るのは困難です。ということで、最終的にはかなり簡略化して、右下の写真のようなフォーク構造（Fork）になりました。私たちは、その日のすべての赤い封筒戦略の集計を作成しました。これは、戦略の 3 つの要素 (赤い封筒インセンティブの合計額、合計時間、合計数) で構成されるベクトルであり、T で表されます。 X は時間 T-1 の交絡変数であり、その日のユーザーの過去の行動と人口統計的属性です。 Y はその日のユーザーの使用時間を表します。これは、翌日のユーザーの保持時間または使用時間の指標となります。ただし、この方法では、赤い封筒間の相互作用など、多くの詳細が無視されているように見えます。しかし、マクロ的な観点から見ると、この戦略はより安定しており、その効果をより適切に測定できます。

#3. 戦略表現と因果モデル

上記の議論を踏まえると、次のステップは、戦略 (治療) をどのように表現するかという核心的な問題です。以前、One-Hot を使用して 3 要素ベクトルに独立して番号を付け、3 つの要素を分離し、時間関数を使用して多変数処理を構築しようとしました。最初の 2 つの方法は理解しやすいため、次に最後の方法を紹介します。上の写真を見てください。 t に関する 3 つの要素の正弦関数をそれぞれ作成しました。つまり、時間 T が与えられると、量、時間間隔、および数をそれぞれ取得できます。戦略の 3 つの要素の表現と同様に、これらの関数に対応するパラメーターを新しいベクトルの要素として使用します。関数を使用して戦略を表す目的は、より詳細な情報を保持することです。最初の 2 つの方法では、戦略の組み合わせを通じて赤封筒の平均量と配布間隔しか知ることができず、関数を使用するとそれをより詳細に表すことができるためです。ただし、この方法ではより多くの変数が導入され、計算がより複雑になる可能性があります。

戦略表現を取得したら、因果効果を推定するための因果モデルを選択できます。 Tの3要素をOne-Hotで表す形で、x-Learnerモデルを用いて各戦略をモデル化し、合計金額が最も小さい戦略をベースライン戦略として全戦略の治療効果を計算・評価します。この場合、効率が非常に低く、モデルに一般化が欠けていると感じるかもしれません。したがって、我々はさらに、今述べた 3 番目の戦略、つまり正弦波関数要素のベクトルを使用して治療を形成する戦略を採用します。次に、単一の DML モデルを使用して、ベースライン戦略と比較してすべての戦略のパフォーマンスを推定します。さらに、y が交絡変数と因果効果の線形重み付けである、つまり y が治療効果と交絡変数を足したものに等しいと仮定して、最適化された DML も作成しました。このようにして、ベクトル要素間の交差項および高次項が人為的に構築されます。これは、非線形関数を導入するために多項式カーネル関数を構築することと同じです。これに基づいて、DML はベースライン戦略と比較して大幅に改善されました。以下の図の分析から、DML モデルはコストが削減され、ROI が向上することがわかります。これは、リソースをより効率的に使用できることを意味します。

先ほどは主にメソッドの抽象化とモデルの選択について説明しましたが、実践のプロセスでは、何をすればよいかなど、よりビジネス指向の問題も見つかります。ワンホットの際のトリートメントはどうですか？現時点では、バッチごとの拡張戦略を導入しました。まず、戦略の3つの要素でシード戦略を立て、その後手動で選別して高品質のシードを保持し、それを拡大します。拡張後は、開始から最初の 2 週間などの期間に基づいて新しい戦略をバッチで開始し、各戦略のランダム トラフィック サイズが一貫しているか同等であることを確認します。このプロセスでは、時間要因の影響は実際に無視され、効果の低い戦略が継続的に置き換えられ、それによって戦略のコレクションが充実します。さらに、時間要因は、ランダム トラフィック戦略が比較できるかどうかに確実に影響します。したがって、対象となるタイム スライスの一貫性を確保するために、タイム スライス ローテーションと同様の方法を構築しました。これにより、戦略に対する時間要因の影響が排除され、取得されたランダム トラフィックをモデルのトレーニングに使用できるようになりました。

#そして、新しい戦略を生み出すにはどうすればよいでしょうか?簡単な方法は、グレード検索または遺伝的アルゴリズムを使用することです。これらは、より一般的な一般的な検索アルゴリズムです。さらに、一部の望ましくない赤いエンベロープ シーケンス タイプを削除するなど、手動による枝刈りを組み合わせることができます。また、オフラインの強化学習手法であるBanditNetを用いて目に見えない戦略、つまり反事実効果を推定し、その推定値を用いて戦略を選択する方法もあります。もちろん、最終的にはオンラインのランダム トラフィックを使用して検証する必要がありますが、その理由は、このオフラインの強化学習手法の分散がおそらく非常に大きくなるからです。

#

4. 戦略的問題と反復

上記の問題に加えて、ビジネス指向の問題もいくつか発生します。最初の質問は、ユーザー ポリシーの更新サイクルは何ですか?すべてのユーザー ポリシーが頻繁に更新されたほうがよいでしょうか?この点に関して、私たちの実際の経験は人によって異なります。たとえば、高頻度ユーザー向けの戦略は、よりゆっくりと変化する必要があります。これは、高頻度ユーザーがインセンティブ額を含めて当社のフォーマットにすでに慣れているためであり、赤い封筒の額が大幅に変更されると、対応する指標に確実に影響を及ぼします。したがって、実際には、高頻度ユーザーに対しては毎週更新戦略を維持し、週に 1 回更新しますが、新規ユーザーの場合は更新サイクルが短くなります。その理由は、私たちは新規ユーザーについてほとんど知らないため、適切な戦略をより迅速に検討し、ユーザーとの対話に基づいて戦略の変更に迅速に対応できるようにしたいと考えているからです。新規ユーザーの行動も非常にまばらであるため、この場合、新規ユーザーまたは一部の低頻度ユーザーを更新するために日次レベルを使用します。さらに、機能ノイズの影響を回避するために戦略の安定性を監視する必要もあります。構築したパイプラインを右側に示します。ここでは、治療効果が安定しているかどうかをモニタリングし、また、今日の戦略と昨日の戦略の違いなど、ユーザーが割り当てた最終的な戦略を量や数も含めて毎日監視します。また、主にデバッグと戦略の安定性を確保するためのクイック再生のために、オンライン戦略のスナップショットを定期的に取得します。さらに、小規模トラフィックに関する実験を実施し、その安定性を監視し、安定性要件を満たす小規模トラフィック実験のみが既存の戦略の置き換えに使用されます。

#2 番目の質問は、新規ユーザーと一部の特別ユーザーのポリシーが独立しているかどうかです。答えは「はい」です。たとえば、新規ユーザーに対しては、最初に強力なインセンティブを提供しますが、その後、インセンティブの強さは時間の経過とともに減衰します。ユーザーが通常のライフサイクルに入った後は、定期的なインセンティブ戦略を導入します。同時に、特別な敏感なグループに対しては、その量に制限ポリシーが適用され、このグループの人々に適応する独立したモデルもトレーニングされます。

3 番目の質問は、アルゴリズム フレームワーク全体において因果推論がどの程度重要かということです。理論的な観点から見ると、因果推論はインセンティブ アルゴリズムに大きなメリットをもたらすため、中核となると考えられます。回帰モデルや分類モデルと比較して、因果推論はビジネス目標と一致しており、本質的に ROI 指向であるため、改善量に関する最適化目標をもたらします。ただし、予算を割り当てる際に、すべてのユーザーに最適な戦略を選択することはできず、因果関係は個人に比べて比較的小さいことを皆さんに思い出していただきたいと思います。予算を割り当てると、ユーザーの因果関係の差異が解消される可能性が非常に高くなります。現時点では、制約付きの最適化が戦略の効果に大きく影響します。したがって、クラスタリングを実行する際には、より良いクラスタリング結果を得るために、ディープ クラスタリング SCCL 手法など、より多くのクラスタリング手法も試しました。また、BNN や Dragonnet などの深層因果モデルの反復もいくつか実行しました。

実践中に、深層因果モデルのオフライン指標は確かに大幅に改善されましたが、オンライン効果は十分に安定していないことがわかりました。欠損値があります。同時に、特徴量計画手法がディープラーニングオンラインモデルの安定性に大きく影響することも分かり、最終的にはDML手法を安定して使用する傾向にあることが分かりました。

# インセンティブのシナリオについての共有はこれくらいにして、次に、私たちのチームの他の 2 人の学生に、供給に関するいくつかの実践方法を共有してもらいたいと思います。需要最適化シナリオと理論的探索。

2. 因果推論と需要と供給の調整

1. ビジネス背景とビジネス モデリング

次Tencent Weishi の需要と供給の観点からの事業背景をご紹介します。 Weishi は短編ビデオ プラットフォームとして、さまざまなカテゴリのビデオを提供しています。閲覧興味が異なるユーザーグループに対して、ユーザーの特性に応じて各カテゴリの露出割合やインベントリ割合を適切に配分し、ユーザーエクスペリエンスとユーザー視聴時間を向上させることが目標です。視聴時間は3秒の高速スワイプ速度指標に基づいて測定され、視聴時間は主に総再生時間に基づいて測定されます。動画カテゴリの露出率や在庫率を調整するにはどうすればよいですか?私たちが主に考慮するのは、一部のカテゴリを比例して増減することです。 増減率はあらかじめ設定された値です。

次に、アルゴリズムを使用して、ユーザー エクスペリエンスと視聴時間を最大化するために、どのカテゴリを増やし、どのカテゴリを減らすかを決定する方法を解決する必要があります。同時に、要件を満たす必要があります。たとえば、総曝露量を制限するいくつかの制約があります。この場所では、3 つの主要なモデリングのアイデアがまとめられています。 最初の は比較的単純なアイデアです。つまり、増加と減少を 0 と 1 の処理変数として直接扱い、その因果効果を推定し、多目的制約付き最適化を実行して次の結果を取得します。最後の戦略。 2 番目のアイデア は、治療をより慎重にモデル化することです。治療は連続変数として扱います。たとえば、カテゴリの露出率は 0 から 1 の間で連続的に変化する変数です。次に、対応する因果効果曲線または因果効果関数をフィッティングし、多目的制約付き最適化を実行して、最終的に最終戦略を取得します。今述べた 2 つの方法は 2 段階の方法であることに注意してください。 3 番目のアイデア 因果効果の推定に制約を導入し、それによって制約を満たす最適な戦略を取得します。これもまた後ほど皆さんにご紹介したい研究内容です。

まず、最初の 2 つのモデリングのアイデアに焦点を当てましょう。注意が必要なモデリングのポイントがいくつかあります。 1 点目は、因果関係推定の精度を確保するためには、母集団を分割し、それぞれの母集団に対する 2 剤治療または継続治療の因果効果を推定する必要があるということです。先ほど Zheng 先生は、Kmeans クラスタリングやディープ クラスタリングの使用など、人々を分類する方法についても言及しました。 2 番目のポイントは、非ランダム実験データに対するモデルの効果をどのように評価するかです。例えば、ABテストを行わずにオフラインでモデルの効果を評価する必要があります。この問題に関しては、オフライン評価用の PPT で上記のインデックスにある論文で言及されているいくつかの指標を参照できます。 3 番目の注意点は、類似カテゴリー間でのクラウディングアウトの問題など、カテゴリー間の相関関係や相互影響を可能な限り考慮する必要があるということです。これらの要因を因果関係の推定に含めることができれば、より良い結果が得られるはずです。

2. 単一グループ × カテゴリの露出比率調整戦略

##次に、これらのモデリングのアイデアを詳しく説明します。まず第一に、最初のモデリング方法は、これら 2 種類の介入を増減する手段を表すために使用される 0 と 1 の治療を定義することです。左側の簡単な因果関係図を参照してください。ここで、x は、過去の操作行動、関連する統計的特性、その他のユーザー属性など、ユーザーのいくつかの特性を表します。 y は注目するターゲットであり、3 秒間の加速率または合計再生時間です。さらに、ユーザーの偶発的な高速スワイプや終了など、いくつかの観察されていない交絡変数にも注意する必要があり、同じユーザーが実際には複数の人によって使用される可能性があり、これもユーザーの複数のアイデンティティの問題です。さらに、推奨戦略の継続的な反復と更新も観測データに影響を及ぼし、ユーザーの興味の移動も観測の範囲外となります。これらの観察されていない交絡変数は、因果効果の推定にある程度影響を与える可能性があります。

このようなモデリング手法では、一般的な因果効果推定手法を解決できます。たとえば、因果関係を推定できる T-Learner または X-Learner、または DML を検討できます。もちろん、この単純なモデリング方法にも問題はあり、例えば、二値化処理でモデル化すると単純化しすぎてしまいます。また、この手法では各カテゴリを個別に考慮しており、カテゴリ間の相関関係は考慮されていない。最後の問題は、質問全体における露出の順序やコンテンツの品質などの特定の要素を考慮していなかったことです。

# 次に、2 番目のモデリングのアイデアを紹介します。すべてのカテゴリをまとめて検討します。たとえば、k 個のビデオ カテゴリがあり、治療を k 次元の原因ベクトルとします。ベクトルの各位置は、映画やテレビのバラエティ番組、MOBA イベントなどのカテゴリを表します。0 と 1 は依然として増加または減少を表します。このとき、多次元ベクトルにおける治療の因果関係推定は、DML アルゴリズムによって解くことができます。通常、すべて 0 である治療ベクトルをコントロールとして扱います。この方法では、各カテゴリが個別に考慮されていないという問題は解決されますが、依然として潜在的な問題がいくつかあります。 1 つ目は、カテゴリが多すぎることによる次元爆発の問題です。次元が増加すると、各位置に 0 と 1 の 2 つの状況が存在するため、潜在的な順列と組み合わせの数が指数関数的に増加し、原因と結果に影響を及ぼします。 . 効果推定の精度により干渉が生じます。また、前述の露出順序やコンテンツなどの要素は考慮されていません。

#バイナリ変数処理のモデリングのアイデアを共有したら、次にさらに多くのことを実行できます。より特徴に即した緻密なモデリングを実現。露出率自体は連続変数であるため、モデリングには連続処理を使用する方が合理的であることに気づきました。このモデリングのアイデアの下では、まず群衆を分割する必要があります。人々のグループごとに、各カテゴリを個別にモデル化し、単一グループ * 単一カテゴリの因果関係曲線を取得します。左の図に示すように、因果関係曲線は、関心のある目標に対するさまざまなカテゴリの割合の影響を表します。このような因果関係曲線を推定するために、主に実行可能な 2 つのアルゴリズム (DR-Net と VC-Net) を紹介します。どちらのアルゴリズムも深層学習のカテゴリに属します。モデルの構造は右の図のとおりです。

まず、DR-Net を紹介します。モデルの入力 x は、最初にいくつかの完全に接続された層を通過して、z と呼ばれる暗黙的な表現を取得します。 DR-Net は、連続処理を複数のブロックに分散する離散化戦略を採用し、各ブロックでサブネットワークをトレーニングしてターゲット変数を予測します。 DR-Net は離散化戦略を採用しているため、最終的に得られる因果効果曲線は厳密には連続ではありませんが、離散化が薄くなるにつれて最終的な推定値は連続曲線に近づきます。もちろん、理想的なセグメンテーションが薄くなると、パラメータが増加し、過学習のリスクが高くなります。

次に、VC-Net について説明します。 VC-Net は、DR-Net の欠点をある程度改善します。まず、VC-Net モデルの入力は依然として X ですが、これはユーザーの特性でもあります。また、いくつかの完全に接続された層の後に、最初に暗黙的な表現 Z を取得します。ただし、Z では、傾向スコアを予測するためのモジュールが最初に接続されます。継続的な治療条件下では、傾向は特定の X 条件下での治療 t の確率密度であり、図では π で表されます。次に、Z 以降のネットワーク構造を見てみましょう。 DR-Net の離散化操作とは異なり、VC-Net は可変係数ネットワーク構造を使用します。つまり、Z 以降の各モデル パラメーターは t に関するパラメーターです。ここで言及した文献の著者は、基底関数法を使用して、各関数を基底関数の線形結合 (θ (t) とも表記) として表現しました。このようにして、関数の推定は、基底関数の線形結合のパラメータ推定になります。このように、モデルのパラメータ最適化は問題なく、VC-Net によって得られる因果関係曲線も連続曲線になります。 VC-Net が解決する目的関数については、いくつかの部分から構成されます。一方では、ターゲットの最終予測の損失の二乗で構成されます。図では μ です。一方で、傾向の確率密度の対数損失からも構成されます。これら 2 つの部分に加えて、目的関数にターゲット正則化と呼ばれるペナルティ項を追加することで、二重のロバストな推定特性を得ることができます。具体的な詳細については、興味のある友人は、上記のインデックスにある 2 つの原著論文を参照してください。

最後に、私たちが共有する研究の一部への道を切り開きましょう。あなたはすぐに。各ビデオ カテゴリの露出割合が多次元の連続ベクトルであることに気づきました。多次元である理由は、複数のビデオ カテゴリがあり、各次元がビデオ カテゴリを表すためです。連続的である主な理由は、各ビデオ カテゴリの露出割合が連続的であり、その値が 0 から 1 の間であるためです。同時に、すべてのビデオ カテゴリの合計露出率が 1 に等しくなければならないという当然の制約があります。したがって、このような多次元連続ベクトルを治療として考えることができます。

#右側に示すベクトルはこの例です。私たちの目標は、合計プレイ時間を最大化する最適な露出率を見つけることです。従来の因果関係の枠組みでは、アルゴリズムがこのような多次元の連続的で制約のない問題を解決することは困難です。次に、この問題に関する調査結果を共有します。

##3. 制約付き連続多変数因果モデルの共有

MDPP Forest この研究は、需要と供給の問題を研究する際にチームによって行われた問題に対する手法の探索と革新的な解決策です。そのとき私たちのチームは、各ユーザーに最適なビデオ カテゴリの露出率をどのように割り当てるかという問題に直面したとき、他の既存の一般的な方法では期待以上の結果を達成できないことに気づきました。したがって、一定期間の試行と改善を経て、私たちのチームが設計した方法はオフラインで良好な結果を達成し、推奨事項と協力して、最終的に特定の戦略的利点を達成することができます。その後、私たちはこの研究を論文にまとめ、幸運にも KDD 2022 で出版することができました。

## 1. 背景と課題

まずは、問題の背景を紹介します。需要と供給の観点から、人気の科学、映画やテレビ、アウトドア フードなどのコンテンツに基づいて、短いビデオをさまざまなカテゴリに分類します。ビデオ カテゴリの露出率とは、ユーザーが視聴するすべてのビデオのうち、これらのさまざまなビデオ カテゴリのそれぞれの割合を指します。ユーザーはカテゴリごとに非常に異なる好みを持っているため、プラットフォームは多くの場合、カテゴリごとに最適な露出率をケースバイケースで決定する必要があります。再注文段階では、さまざまな種類のビデオの推奨が制御されます。同社にとっての大きな課題は、各ユーザーのプラットフォーム滞在時間を最大化するために、ビデオ露出の最適な比率をどのように割り当てるかということだ。

#このような問題の主な難点は、次の 3 点にあります。 1 つ目は、短いビデオの推奨システムでは、各ユーザーが視聴するビデオがそのユーザー自身の特性と非常に強い相関関係を持っていること、これが選択バイアスであるということです。したがって、因果推論に関連するアルゴリズムを使用してバイアスを排除する必要があります。 2 つ目は、ビデオ カテゴリの露出率が継続的、多次元的かつ限定的な扱いであることです。現在、因果推論とポリシー最適化の分野では、このような複雑な問題に対して非常に成熟した方法はありません。 3つ目は、オフラインデータでは各人の真の最適曝露率をアプリオリに知ることができないため、この方法を評価することが難しいことです。実際の環境では、推奨におけるサブリンクにすぎません。最終的な実験結果は、この方法の精度を判断することはできません。#それ自体の計算目標に対して。したがって、このシナリオの問題を正確に評価することは困難です。効果評価の方法については後ほどご紹介します。

#2. 問題定義

私たちまず、データを統計学の因果関係図に抽象化します。その中でもベクター。 Y はユーザーの視聴時間であり、タスクの目標に対する応答です。私たちのモデリングの目標は、ユーザーの視聴時間の期待を最大化するために、特定のユーザー特性 X の下で高次元の最適なビデオ カテゴリ露出率を与えることです。この問題は単純に因果関係三元図で表現されているように見えますが、先に述べたように大きな問題が存在します。我々は、複数のカテゴリの露出率をカテゴリの露出率で考慮して扱います。比率は多次元ベクトルを構築します。連続値であり、ベクトルの合計は 1 です。この問題はさらに複雑です。

3. メソッドの紹介—最大差異優先点 (MDP2) フォレスト

##この点において、私たちの手法も因果の森（因果の森）に基づいています。一般的な因果決定木は、1 次元の離散値を使用した治療問題のみを解決できます。中間分割基準関数の計算を改善することにより、分割中にいくつかの高次元連続情報を追加し、高次元連続値と制約された処理の問題を解決できます。

① メソッドの紹介 - 連続問題

まず、継続的な治療の問題を解決します。図に示すように、Y に対する T の効果は連続曲線です。まず、これが単調増加曲線であると仮定しましょう。データ内のすべての治療値について、それをトラバースして左右のサンプルの Y 平均を計算し、左側の Y 平均と右側の Y 平均の差が最も大きい点を見つけます。平均因果利益が最大となる点。この点を最大差分点と呼びます。これは、連続治療空間上の最も効率的な点であり、治療によって Y が大幅に変化する可能性があることを意味します。最大差分ポイントは、単一次元で取得したいポイントです。

ただし、今述べた方法は単調増加曲線にのみ適しています。しかし実際には、ほとんどの問題、特に露出率の問題はそれほど良くありません。この問題に関しては、効果曲線は一般的に山型になります。つまり、最初に増加し、その後減少します。ユーザーが好む動画をより多く推薦すると、ユーザーの視聴時間を増やすことができますが、このタイプの動画を推薦しすぎると、動画の推薦全体が非常に単調で退屈になり、また、他のユーザーが好む動画タイプの露出スペースを圧迫してしまいます。のように。したがって、曲線は一般に山型ですが、他の形状の場合もあります。あらゆる形状の T カーブに適応するには、積分演算を実行する必要があります。つまり、累積する値の範囲間隔を見つける必要があります。累積曲線上で、左側と右側の平均値と、両側の平均値の差が最も大きくなる点（図の五芒星など）も計算します。絵。この点は、最大の優先差点と呼ぶことができ、それが当社の MDPP です。

#② 手法の紹介 - 高次元問題

上で連続問題の解決方法を紹介しましたが、先ほど述べた曲線は 1 次元にすぎず、単一のビデオ カテゴリに対応します。次に、ヒューリスティック次元トラバーサルのアイデアを使用して、多次元の問題を解決します。分類スコアを計算するとき、ヒューリスティックなアイデアを使用して K 次元をランダムに並べ替え、各次元で D 個の指標の集計を計算します。つまり、合計演算を実行します。高次元情報エントロピーとして D* を求め、すべての MDPP の合計が 1 になるという制約を考慮します。ここでは、K 次元を通過しても MDPP の合計が 1 に達しない場合の 2 つの状況を考慮する必要があります。この状況に対応して、すべての MDPP の合計を加算し、1 に正規化します。 2 番目のケースは、K 次元より小さい K' 次元のみをトラバースすると、MDPP の合計が 1 に達する場合です。このため、トラバーサルを停止し、制約を考慮できるように、MDPP を残りの「リソース量」 (1 から以前に計算された MDPP 値の合計を引いたもの) に設定します。

#さらに、上記のツリー構造にフォレストも導入します。大きく分けて2つの意味があります。 1 つ目は、複数の学習器を使用してモデルの堅牢性を強化できる、従来のバギング アンサンブルのアイデアです。 2 つ目は、次元トラバーサルでは、ノードが分割されるたびに K' 次元のみが計算され、一部の次元は含まれないことです。各次元が分割に参加する機会を均等にするには、複数のツリーを構築する必要があります。

##③ メソッド導入 - アルゴリズムの高速化

もう 1 つの問題があります。アルゴリズムには 3 レベルのトラバーサルが含まれているため、すべてのツリー モデルには固有値トラバーサルに加えて、追加の次元トラバーサルと MDPP 検索トラバーサルが必要です。このような 3 層のトラバースでは効率が非常に低くなります。したがって、固有値トラバーサルと MDPP トラバーサルに加重分位グラフ法を使用し、分位点での対応する結果のみを計算することで、アルゴリズムの複雑さを大幅に軽減できます。同時に、これらの分位点が「累積値の範囲」の境界点であることもわかり、計算量と保存量を大幅に削減できます。 q 分位数があると仮定すると、サンプル数と各分位間隔の y の平均値を取得するには q 回計算するだけで済みます。このようにして、両側の平均値の差 d を計算するたびに、 q値を左側に分割する必要があります。右側の2つの部分については、各区間の平均値の加重合計を行うだけです。分位点の左右にあるすべてのサンプルの平均を再計算する必要はなくなりました。以下の実験部分に入りましょう。

4. 実験計画

① 実験計画 - 指標

実験評価は本質的に戦略です。という問題があるので、戦略評価に関する指標を紹介します。 1 つ目は Main Regret で、戦略全体のリターンと理論上の最適リターンとの間のギャップを測定します。もう 1 つは、多次元治療における各治療次元の推定値と最適値との間のギャップを測定するために使用される主治療二乗誤差です。どちらの指標も小さいほど良いです。しかし、この 2 つの評価指標を設定する際に生じる最大の問題は、最適な値をどうやって決めるかということです。

② 実験計画法 - コントラスト法

比較方法をご紹介します。 1 つは因果推論で一般的に使用される 2 つの方法です。1 つは完全な統計理論を備えた DML で、もう 1 つはネットワーク モデル DR-Net と VC-Net です。これらの手法は 1 次元の問題のみを処理できますが、この記事の問題では、多次元の問題に対処できるようにいくつかの調整を行っています。つまり、最初に各次元の絶対値を計算してから正規化を実行します。次の 2 つの論文には、OPE および OCMD と呼ばれる戦略最適化手法もあります。これら 2 つの記事では、その方法が多次元問題に適していると述べていますが、次元が多すぎる場合にはこれらの方法が効果的であることが難しいとも指摘しています。

③ 実験設計シミュレーション データ セット

#モデルの効果を簡単かつ直接比較するために、現実世界の問題をシミュレートし、シミュレーション データセットの簡易バージョンを生成しました。特徴空間 x は、ユーザー特徴の 6 次元と 2 つの行動特徴を表します。異なる特性を持つサンプルについては、まずその最適な戦略を仮定します。図に示すように、たとえば、45 歳未満で、教育レベルが 2 を超え、行動特性が 0.5 を超えるユーザーは、6 つのビデオ カテゴリで最高です。左側の式を使用して、まずユーザーの露出戦略をランダムに生成し、次に露出戦略と実際の最適な戦略の間のギャップ、およびシミュレートされたユーザーの継続時間を計算します。戦略がユーザーの最適な戦略に近い場合、ユーザーの継続時間 y は長くなります。このようにして、このようなデータセットを生成しました。このシミュレートされたデータセットの利点は、最適値を直接仮定できるため、評価に非常に便利であること、もう 1 つは、データが比較的単純であるため、アルゴリズムの結果の分析が容易であることです。

# シミュレートされたデータセットの実験結果を見てみましょう。先ほど述べたように、このタイプの母集団に対して、対応する治療の平均値を計算するためのさまざまな方法が提供されています。最初の行は理論上の最適値、2 行目は MDPP フォレスト、3 行目は MDPP フォレストに基づいており、分割基準にいくつかのペナルティ項を追加しています。私たちの方法と理論上の最適値の間のギャップは非常に小さいことがわかります。他の方法は特に極端ではありませんが、比較的均一です。さらに、右側の MR と MTSE の図から、私たちの 2 つの方法には非常に明白な利点もあります。

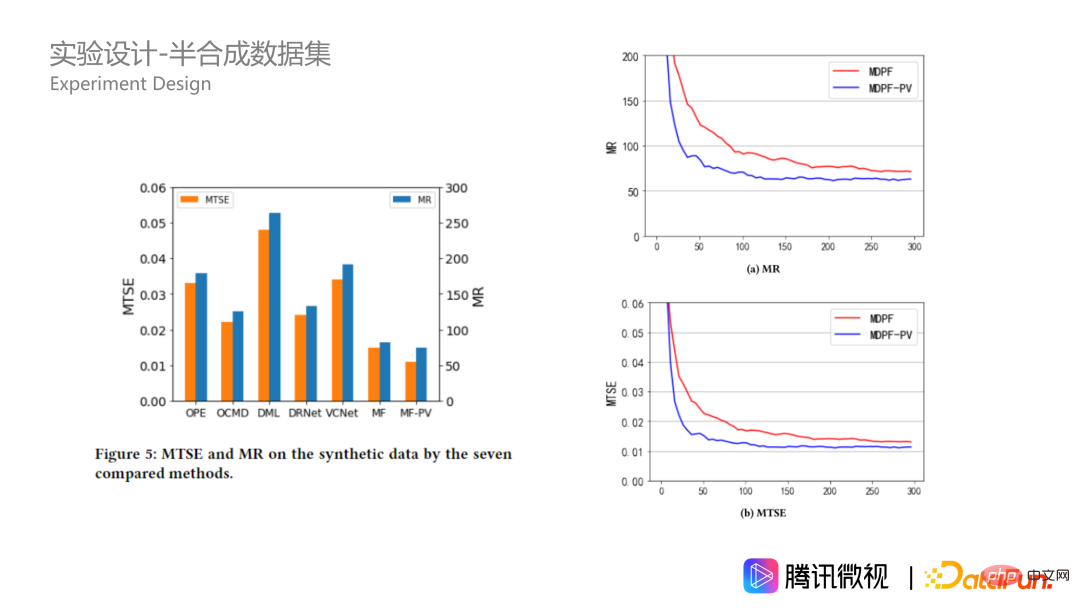
④ 実験計画 - 半合成データ セット

シミュレーション データ セットに加えて、実際のビジネスに基づいた半合成データも構築しました。データ。データは Tencent Weishi プラットフォームから取得されます。 Xi はユーザーの 20 次元特性を表し、治療 ti は 10 次元ベクトルを形成する多次元ビデオカテゴリ露出率を表し、yi(ti) は i 番目のユーザーの使用時間を表します。実際のシナリオの特徴の 1 つは、ユーザーの実際の最適なビデオ露出率を知ることができないことです。したがって、クラスター中心規則に従って関数を構築し、実際の y を置き換える仮想 y を生成することで、サンプルの y の規則性が向上します。具体的な公式についてはここでは説明しませんので、興味のある方は原文を読んでください。なぜこのようなことが可能なのでしょうか?なぜなら、私たちのアルゴリズムの鍵は、x と t の間の交絡効果、つまりオンライン ユーザーが偏った戦略の影響を受けることを解決できる必要があるからです。戦略の効果を評価するために、x と t のみを保持し、問題をより適切に評価するために y を変更します。

半合成データでも、私たちのアルゴリズムは大幅に優れたパフォーマンスを発揮し、シミュレートされたデータセットの利点はさらに大きくなります。これは、データが複雑な場合、MDPP フォレスト アルゴリズムがより安定していることを示しています。さらに、合成データのハイパーパラメーター、つまりフォレストのサイズを見てみましょう。右下の図では、フォレスト サイズが大きくなるにつれて、2 つの分割基準の下で指標がより良く収束することがわかります。ペナルティ項がある方が常に優れており、ツリーが 100 本の場合はより良く到達します。最適な効果は 250 個のツリーで達成されますが、ある程度の過剰適合が発生します。

4. Q&A セッション

Q: なぜトラバースするのか露出が 1 を超えた場合でも正規化は機能しますか?

#A: 私の理解では、私たちが行っているのは露出比率の制約の最適化であるため、このプロセスでは相対的な値になります。トラバースの過程で、最適な分割ポイントを探し、どのカテゴリーを優先すべきか、露出の割合を見つけます。このプロセスでは、比例的に拡大縮小されることが確認できれば問題ありません。

#私も同じビューを持っています。比例して拡大縮小できます。 1 は強い制約であるため、最初に計算した値は正確に 1 にはなりませんが、それよりも低いか高い値になります。それ以上の数がある場合、強い制約という特有の条件を満たす方法はなく、正規化された考え方を使用する方が自然です。各カテゴリ間の相対的な大小関係を考慮するためです。絶対的な価値の問題ではなく、相対的な大きさの関係が重要だと思います。

以上がミクロビューのインセンティブと需要と供給のシナリオにおける因果推論の適用の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。