ホームページ >Java >&#&チュートリアル >Java データ構造 AVL ツリーの例の分析
Java データ構造 AVL ツリーの例の分析
- 王林転載
- 2023-04-29 22:07:051424ブラウズ

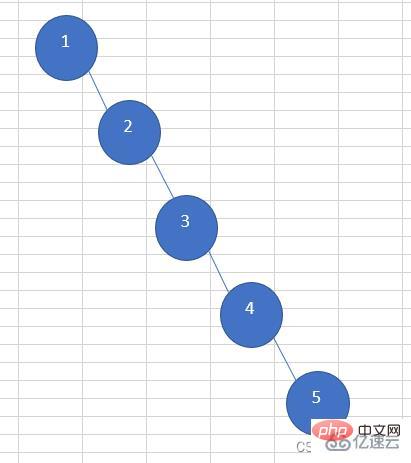 こんな感じ 二分木の検索効率は連結リストよりもさらに低いです。この問題を解決するのが、探索二分木に基づいて現れるバランス二分木(AVLツリー)です。平衡二分木 (AVL ツリー) のノードの左右のサブツリー間の高さの差の絶対値が 1 より大きい場合、それらの高さの差は回転操作によって減少します。
こんな感じ 二分木の検索効率は連結リストよりもさらに低いです。この問題を解決するのが、探索二分木に基づいて現れるバランス二分木(AVLツリー)です。平衡二分木 (AVL ツリー) のノードの左右のサブツリー間の高さの差の絶対値が 1 より大きい場合、それらの高さの差は回転操作によって減少します。
- それ自体が最初に
二分探索木です
。 - 各ノードの左右のサブツリーの
高さの差の絶対値 (バランス係数) は最大 1
です。言い換えれば、AVL ツリーは本質的に、バランシング関数を備えた二分探索ツリー (二分ソート ツリー、二分探索ツリー) です。 - ノードを挿入または削除する場合、ノードの左右のサブツリー間の高さの差の絶対値は 1 より大きくなります。この場合、次の値を渡す必要があります。
左回転
および右回転操作により、二分木は再び平衡状態に達します。
バランス係数 (balanceFactor)
- ノードの左側のサブツリーと右側のサブツリー
高さの差は ###。
AVL ツリー内のノードの BF は、 - -1、0、および 1 のみです。
AVL ツリーに必要な単純なメソッドと属性を次に示します:
public class AVLTree <E extends Comparable<E>>{
class Node{
E value;
Node left;
Node right;
int height;
public Node(){}
public Node(E value){
this.value = value;
height = 1;
left = null;
right = null;
}
public void display(){
System.out.print(this.value + " ");
}
}
Node root;
int size;
public int size(){
return size;
}
public int getHeight(Node node) {
if(node == null) return 0;
return node.height;
}
//获取平衡因子(左右子树的高度差,大小为1或者0是平衡的,大小大于1不平衡)
public int getBalanceFactor(){
return getBalanceFactor(root);
}
public int getBalanceFactor(Node node){
if(node == null) return 0;
return getHeight(node.left) - getHeight(node.right);
}
//判断一个树是否是一个平衡二叉树
public boolean isBalance(Node node){
if(node == null) return true;
int balanceFactor = Math.abs(getBalanceFactor(node.left) - getBalanceFactor(node.right));
if(balanceFactor > 1) return false;
return isBalance(node.left) && isBalance(node.right);
}
public boolean isBalance(){
return isBalance(root);
}
//中序遍历树
private void inPrevOrder(Node root){
if(root == null) return;
inPrevOrder(root.left);
root.display();
inPrevOrder(root.right);
}
public void inPrevOrder(){
System.out.print("中序遍历:");
inPrevOrder(root);
}}RR(左利き)
下に示すように、ツリーの右側のサブツリーの右側のサブツリーにノードを挿入すると、バイナリ ツリーのバランスが崩れます。バランスの取れたバイナリ ツリーに 5 を挿入すると、ツリーのバランスが崩れます。この時点で、このとき、次のように左折操作が必要になります。
コードは次のとおりです。 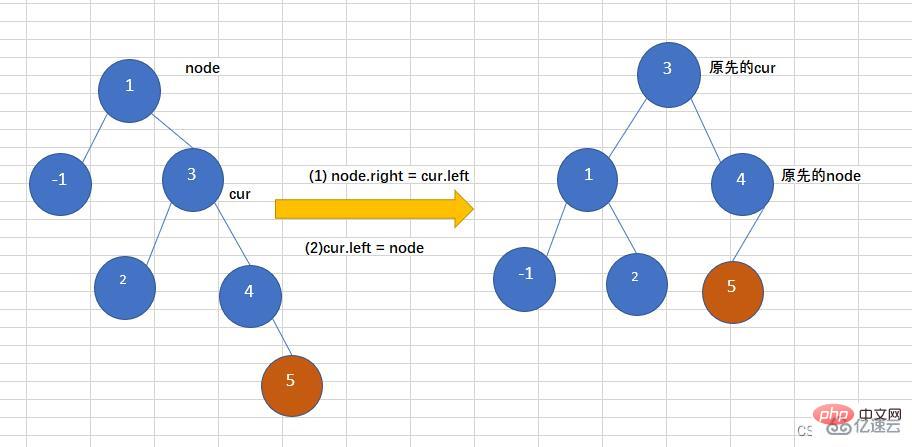
//左旋,并且返回新的根节点
public Node leftRotate(Node node){
System.out.println("leftRotate");
Node cur = node.right;
node.right = cur.left;
cur.left = node;
//跟新node和cur的高度
node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
return cur;
}LL (右回転)
ノードを挿入します。 AVL ツリーの左サブツリーの左サブツリーを追加すると、下図のように二分木が不均衡になります。バランスの取れた二分木に 2 を挿入すると、ツリーがアンバランスになります。このとき、左折は次のような操作が必要です:
コードは次のとおりです: 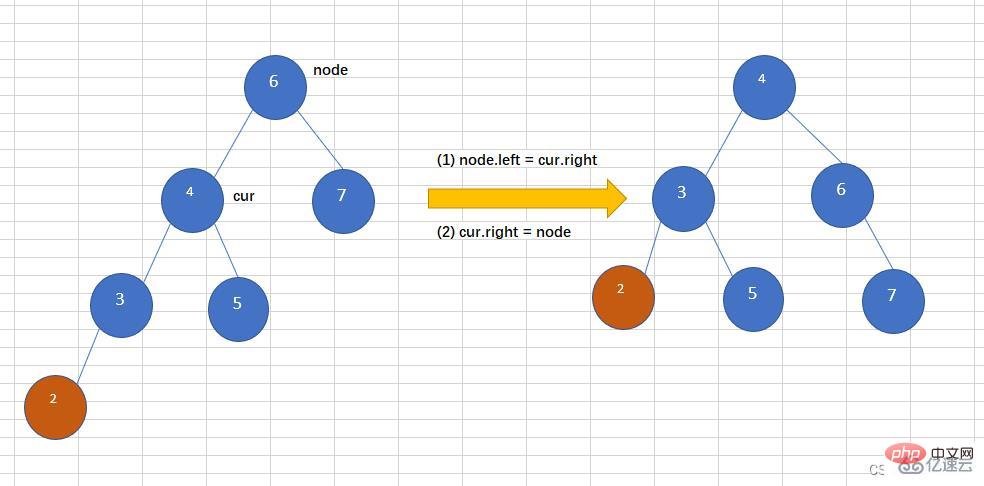
//右旋,并且返回新的根节点
public Node rightRotate(Node node){
System.out.println("rightRotate");
Node cur = node.left;
node.left = cur.right;
cur.right = node;
//跟新node和cur的高度
node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
return cur;
}LR (最初に左に回転し、次に右に回転します)
AVL ツリー
の左サブツリーの右サブツリー。その結果、ツリーのバランスが崩れています。最初に 左サブツリーを修正する必要があります。左回転 を実行してから、回転します ツリー全体を右に 、以下の図に示すように、ノード 5.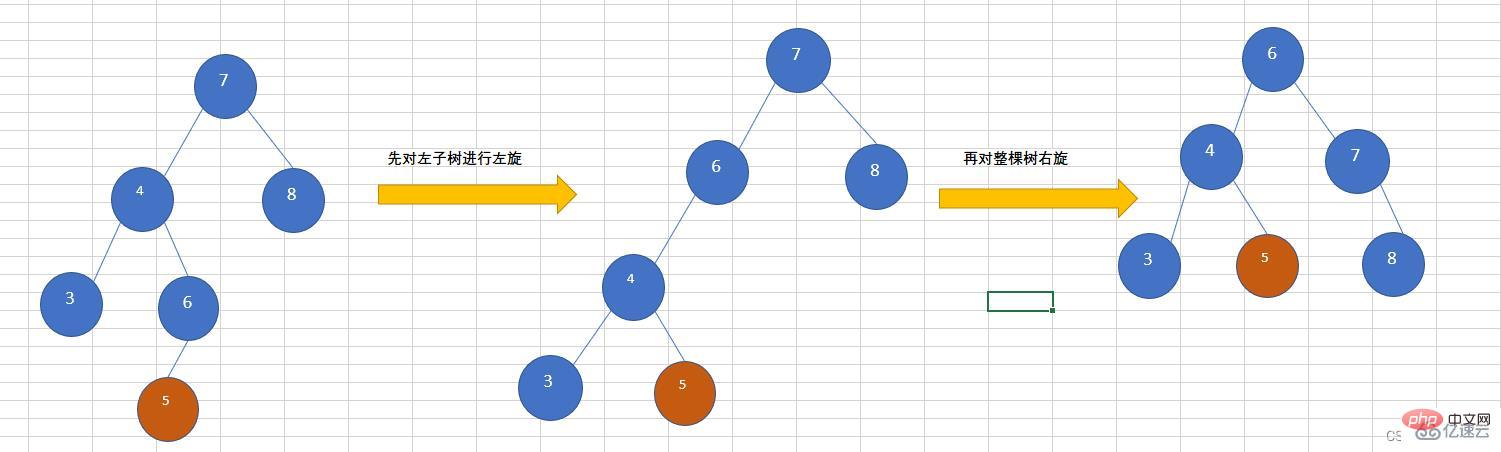 RL を挿入します (最初に右に回転し、次に左に回転します)
RL を挿入します (最初に右に回転し、次に左に回転します)
AVL ツリー
の右サブツリーの左サブツリー にノードを挿入すると、ツリーのバランスが崩れます。最初に 右サブツリー を右回転する必要があります。次に ツリー全体を左回転します。 下の図に示すように、ノード 2 を挿入します。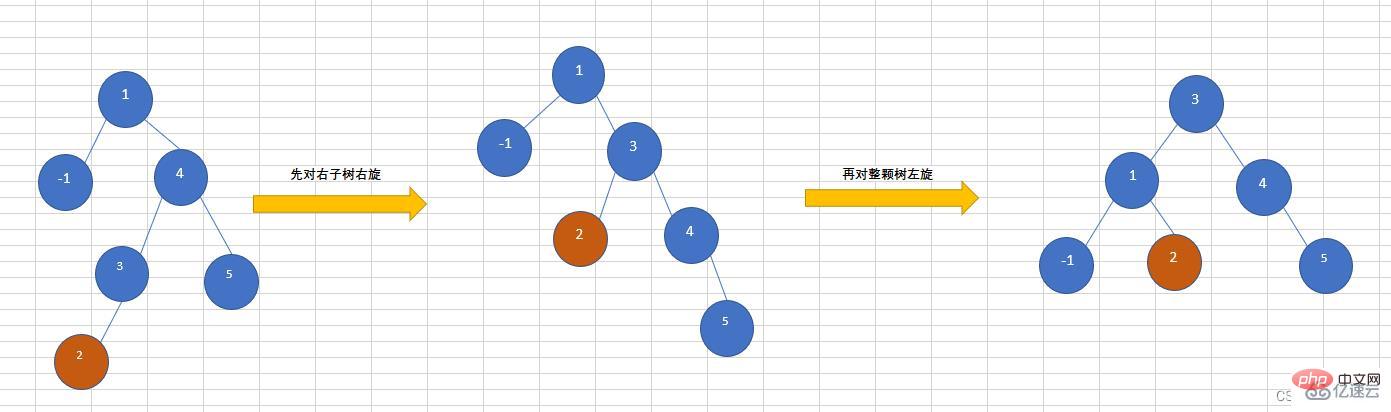 ノードを追加
ノードを追加
//添加元素
public void add(E e){
root = add(root,e);
}
public Node add(Node node, E value) {
if (node == null) {
size++;
return new Node(value);
}
if (value.compareTo(node.value) > 0) {
node.right = add(node.right, value);
} else if (value.compareTo(node.value) < 0) {
node.left = add(node.left, value);
}
//跟新节点高度
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
//获取当前节点的平衡因子
int balanceFactor = getBalanceFactor(node);
//该子树不平衡且新插入节点(导致不平衡的节点)在左子树的左子树上,此时需要进行右旋
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
return rightRotate(node);
}
//该子树不平衡且新插入节点(导致不平衡的节点)在右子树子树的右子树上,此时需要进行左旋
else if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
return leftRotate(node);
}
//该子树不平衡且新插入节点(导致不平衡的节点)在左子树的右子树上,此时需要先对左子树左旋,在整个树右旋
else if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
//balanceFactor < -1 && getBalanceFactor(node.left) > 0
//该子树不平衡且新插入节点(导致不平衡的节点)在右子树的左子树上,此时需要先对右子树右旋,再整个树左旋
else if(balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}ノードを削除
//删除节点
public E remove(E value){
root = remove(root,value);
if(root == null){
return null;
}
return root.value;
}
public Node remove(Node node, E value){
Node retNode = null;
if(node == null)
return retNode;
if(value.compareTo(node.value) > 0){
node.right = remove(node.right,value);
retNode = node;
}
else if(value.compareTo(node.value) < 0){
node.left = remove(node.left,value);
retNode = node;
}
//value.compareTo(node.value) = 0
else{
//左右节点都为空,或者左节点为空
if(node.left == null){
size--;
retNode = node.right;
}
//右节点为空
else if(node.right == null){
size--;
retNode = node.left;
}
//左右节点都不为空
else{
Node successor = new Node();
//寻找右子树最小的节点
Node cur = node.right;
while(cur.left != null){
cur = cur.left;
}
successor.value = cur.value;
successor.right = remove(node.right,value);
successor.left = node.left;
node.left = node.right = null;
retNode = successor;
}
if(retNode == null)
return null;
//维护二叉树平衡
//跟新height
retNode.height = Math.max(getHeight(retNode.left),getHeight(retNode.right));
}
int balanceFactor = getBalanceFactor(retNode);
//该子树不平衡且新插入节点(导致不平衡的节点)在左子树的左子树上,此时需要进行右旋
if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0) {
return rightRotate(retNode);
}
//该子树不平衡且新插入节点(导致不平衡的节点)在右子树子树的右子树上,此时需要进行左旋
else if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0) {
return leftRotate(retNode);
}
//该子树不平衡且新插入节点(导致不平衡的节点)在左子树的右子树上,此时需要先对左子树左旋,在整个树右旋
else if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
retNode.left = leftRotate(retNode.left);
return rightRotate(retNode);
}
//该子树不平衡且新插入节点(导致不平衡的节点)在右子树的左子树上,此时需要先对右子树右旋,再整个树左旋
else if(balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
retNode.right = rightRotate(retNode.right);
return leftRotate(retNode);
}
return retNode;
}以上がJava データ構造 AVL ツリーの例の分析の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
声明:
この記事はyisu.comで複製されています。侵害がある場合は、admin@php.cn までご連絡ください。

