ホームページ >Java >&#&チュートリアル >Javaコードで古典的なソートアルゴリズムを使用する方法
Javaコードで古典的なソートアルゴリズムを使用する方法
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB転載
- 2023-04-29 20:49:051591ブラウズ
ソート アルゴリズムは、「データ構造とアルゴリズム」の最も基本的なアルゴリズムの 1 つです。
並べ替えアルゴリズムは、内部並べ替えと外部並べ替えに分けることができます。内部並べ替えはメモリ内のデータ レコードを並べ替えることですが、外部並べ替えは、並べ替えられたデータが非常に大きく、並べ替えられたすべてのレコードを一度に収容できないためです。ソート処理中は外部メモリにアクセスする必要があります。一般的な内部ソート アルゴリズムには、挿入ソート、ヒル ソート、選択ソート、バブル ソート、マージ ソート、クイック ソート、ヒープ ソート、基数ソートなどがあります。画像で要約:
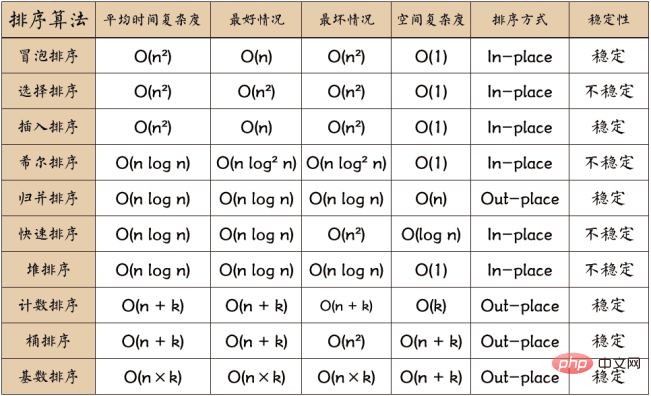
時間計算量について:
二乗次数 (O(n2 ))直接挿入、直接選択、バブルソートなど、さまざまなタイプの単純なソートをソートします。
線形対数順序 (O(nlog2n)) ソート クイック ソート、ヒープ ソート、およびマージ ソート。
O(n1 §)) sort、§ は 0 から 1 までの定数です。ヒルソート。
バケットおよびビンのソートに加えて、線形順序 (O(n)) ソート、基数ソート。
安定性について:
安定したソート アルゴリズム: バブル ソート、挿入ソート、マージ ソート、基数ソート。
は安定したソート アルゴリズムではありません: 選択ソート、クイック ソート、ヒル ソート、ヒープ ソート。
用語の説明:
n: データスケール
k: 「バケット」の数
インプレース:占有された固定メモリ、追加メモリの占有なし
アウトプレイス: 追加メモリの占有
安定性: ソート後の 2 つの等しいキー値の順序は、ソート前の順序と同じです
1. バブル ソート
バブル ソートも、シンプルで直感的な並べ替えアルゴリズムです。ソート対象のシーケンスを繰り返し調べて、一度に 2 つの要素を比較し、順序が間違っている場合はそれらを交換します。配列を訪問する作業は、それ以上の交換が必要なくなるまで繰り返されます。これは、配列がソートされたことを意味します。このアルゴリズムの名前は、小さい要素がスワッピングによって配列の先頭にゆっくりと「浮動」するという事実に由来しています。
バブルソートは最も単純な並べ替えアルゴリズムの一つで、単語帳のAbandonと同じような感じで、毎回***のページにあるので一番馴染みがあります。バブルソートにはフラグを設定するという別の最適化アルゴリズムもあり、シーケンスの走査中に要素が交換されない場合、シーケンスが正しいことを証明します。しかし、この改善はパフォーマンスの向上にはあまり役に立ちません。
1. アルゴリズムのステップ
隣接する要素を比較します。最初のものが 2 番目のものより大きい場合は、両方を交換します。
最初のペアから最後のペアまで、隣接する要素の各ペアに対して同じことを行います。この手順が完了すると、*** 要素は *** 番号になります。
** 1 つを除くすべての要素に対して上記の手順を繰り返します。
比較する数値のペアがなくなるまで、要素の数を減らしながら上記の手順を繰り返します。
2. GIF デモ
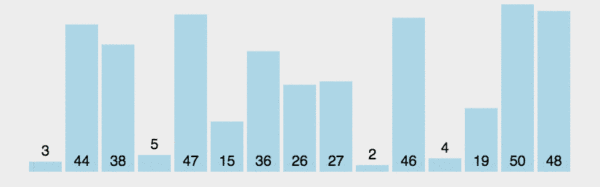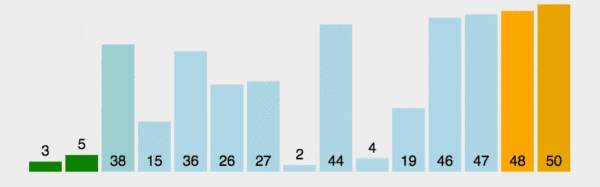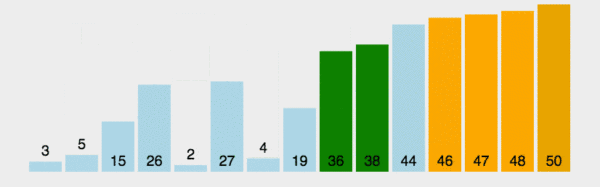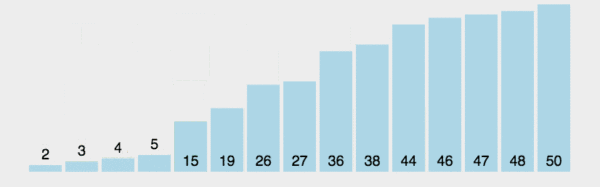
3. 最速の時間はいつですか
入力データがすでに正の順序になっている場合 (すでに正の順序になっていますが、バブル ソートは何に役立ちますか?)。
4. 最も遅いのはいつですか?
入力データが逆の順序である場合 (データを逆の順序で出力する for ループを記述するだけですが、なぜそうすべきなのでしょうか)あなたを利用しますか?バブルソートはどうですか、空いていますか?)
5. Java コードの実装
public class BubbleSort implements IArraySort { @Override public int[] sort(int[] sourceArray) throws Exception { // 对 arr 进行拷贝,不改变参数内容 int[] arr = Arrays.copyOf(sourceArray, sourceArray.length); for (int i = 1; i arr[j + 1]) { int tmp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = tmp; flag = false; } } if (flag) { break; } } return arr; } }
2. 選択ソート
選択ソートは、シンプルで直感的な並べ替えアルゴリズムです。どのようなデータが入力されても、時間計算量は O(n 2;) です。したがって、使用する場合はデータサイズが小さいほど良いです。唯一の利点は、追加のメモリ空間を占有しないことです。
1. アルゴリズムのステップ
#まず、ソートされていないシーケンス内で最小の (大きな) 要素を見つけて、それをシーケンスの開始位置に保存します。ソートされたシーケンス
次に、ソートされていない残りの要素から最小 (大きい) 要素を検索し、それをソートされたシーケンスの最後に置きます。
すべての要素が並べ替えられるまで、2 番目の手順を繰り返します。
#2. アニメーションのデモ
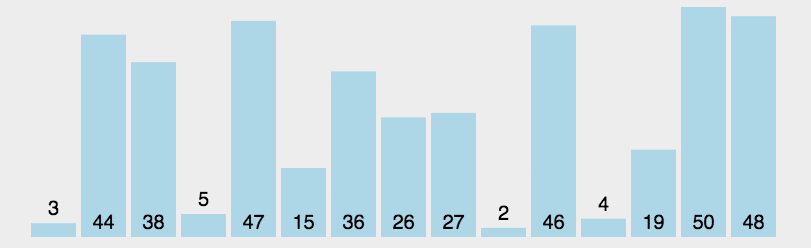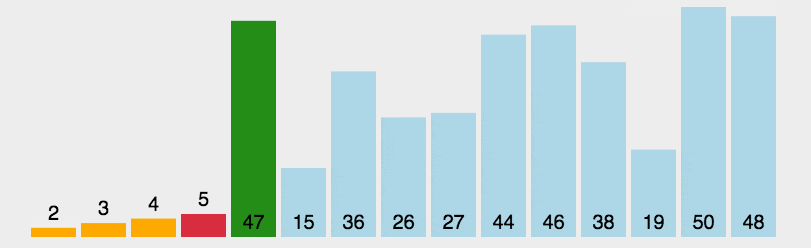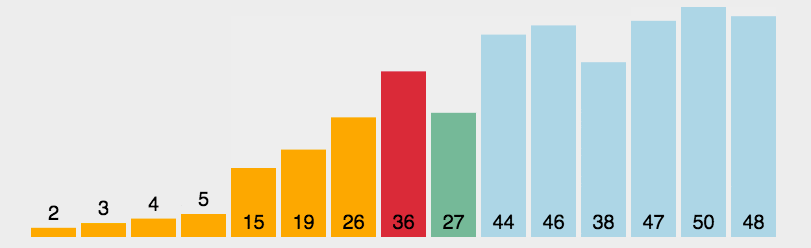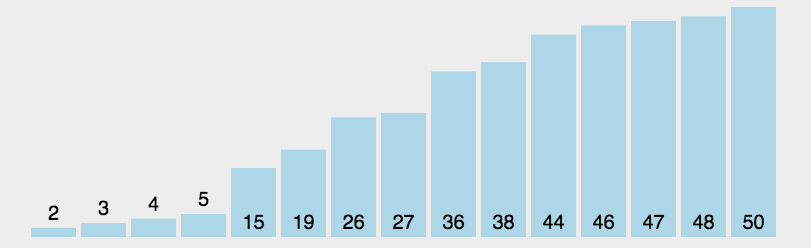
3. Java コードの実装
public class SelectionSort implements IArraySort { @Override public int[] sort(int[] sourceArray) throws Exception { int[] arr = Arrays.copyOf(sourceArray, sourceArray.length); // 总共要经过 N-1 轮比较 for (int i = 0; i <p>3. 挿入ソート<strong></strong></p>挿入ソートのコード実装はバブル ソートや選択ソートほど単純で粗雑ではありませんが、その原理は最も理解しやすいはずです。 , なぜなら、ポーカーをプレイしたことがある人なら、すぐに理解できるはずだからです。挿入ソートは、最もシンプルで直感的なソート アルゴリズムです。順序付けされたシーケンスを構築することで機能します。ソートされていないデータの場合は、ソートされたシーケンス内で後ろから前にスキャンして、対応する位置を見つけて挿入します。 <p></p>挿入ソートには、バブル ソートと同様、分割半挿入と呼ばれる最適化アルゴリズムもあります。 <p></p><p><strong>1. 算法步骤</strong></p>
将***待排序序列***个元素看做一个有序序列,把第二个元素到***一个元素当成是未排序序列。
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
2. 动图演示
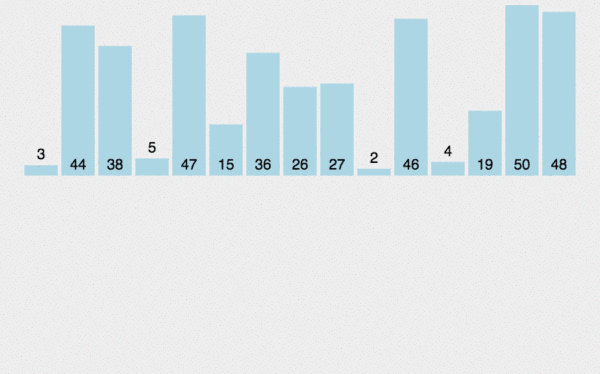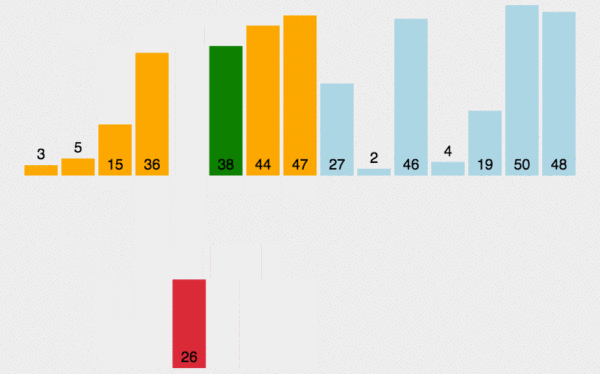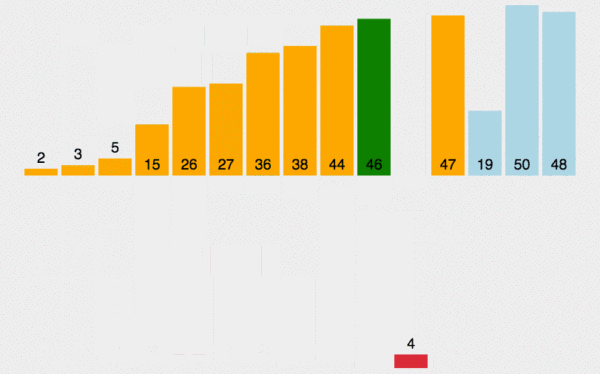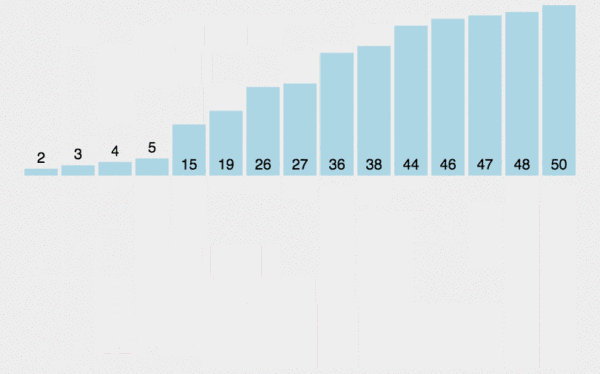
3. Java 代码实现
public class InsertSort implements IArraySort { @Override public int[] sort(int[] sourceArray) throws Exception { // 对 arr 进行拷贝,不改变参数内容 int[] arr = Arrays.copyOf(sourceArray, sourceArray.length); // 从下标为1的元素开始选择合适的位置插入,因为下标为0的只有一个元素,默认是有序的 for (int i = 1; i 0 && tmp <p><strong>四、希尔排序</strong></p><p>希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。</p><p>希尔排序是基于插入排序的以下两点性质而提出改进方法的:</p>
插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率
但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序。
1. 算法步骤
选择一个增量序列 t1,t2,……,tk,其中 ti > tj, tk = 1;
按增量序列个数 k,对序列进行 k 趟排序;
每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
2. Java 代码实现
public class ShellSort implements IArraySort { @Override public int[] sort(int[] sourceArray) throws Exception { // 对 arr 进行拷贝,不改变参数内容 int[] arr = Arrays.copyOf(sourceArray, sourceArray.length); int gap = 1; while (gap 0) { for (int i = gap; i = 0 && arr[j] > tmp) { arr[j + gap] = arr[j]; j -= gap; } arr[j + gap] = tmp; } gap = (int) Math.floor(gap / 3); } return arr; } }
五、归并排序
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
作为一种典型的分而治之思想的算法应用,归并排序的实现由两种方法:
自上而下的递归(所有递归的方法都可以用迭代重写,所以就有了第 2 种方法)
自下而上的迭代
在《数据结构与算法 JavaScript 描述》中,作者给出了自下而上的迭代方法。但是对于递归法,作者却认为:
However, it is not possible to do so in JavaScript, as the recursion goes too deep for the language to handle.
然而,在 JavaScript 中这种方式不太可行,因为这个算法的递归深度对它来讲太深了。
说实话,我不太理解这句话。意思是 JavaScript 编译器内存太小,递归太深容易造成内存溢出吗?还望有大神能够指教。
和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是 O(nlogn) 的时间复杂度。代价是需要额外的内存空间。
1. 算法步骤
申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
设定两个指针,最初位置分别为两个已经排序序列的起始位置;
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
重复步骤 3 直到某一指针达到序列尾;
将另一序列剩下的所有元素直接复制到合并序列尾。
2. 动图演示
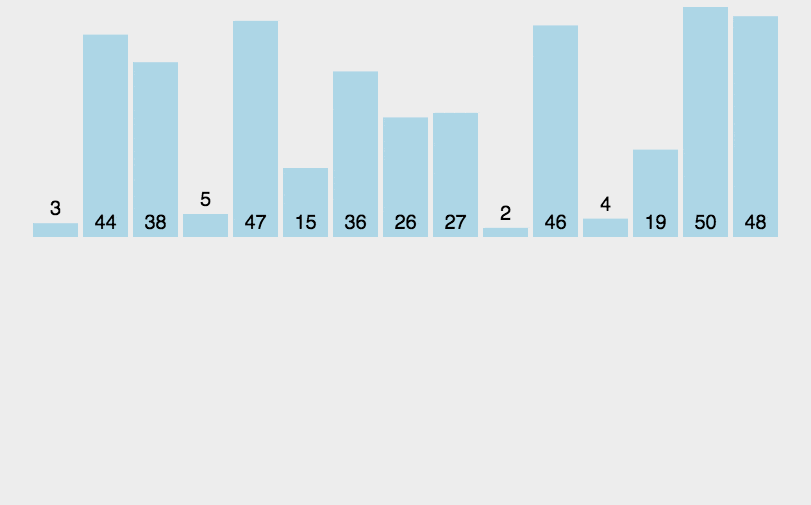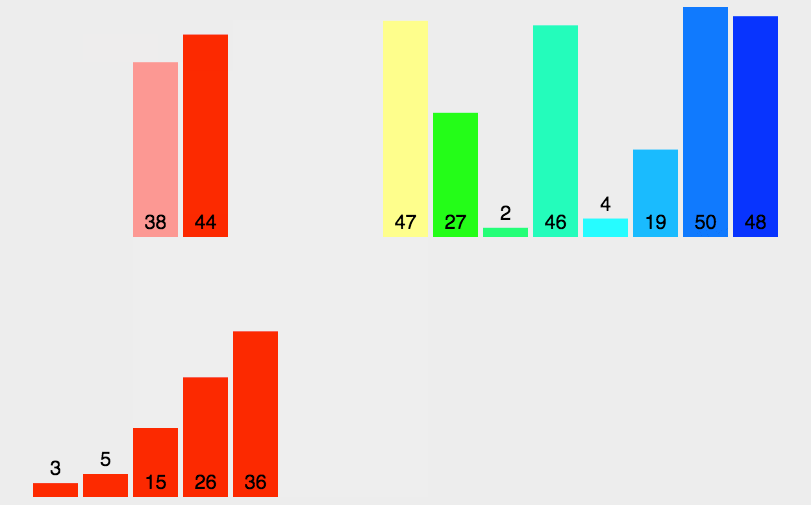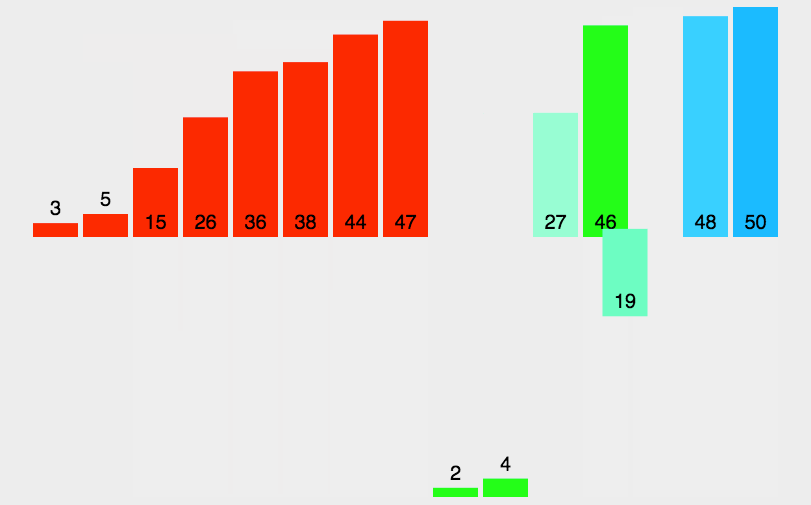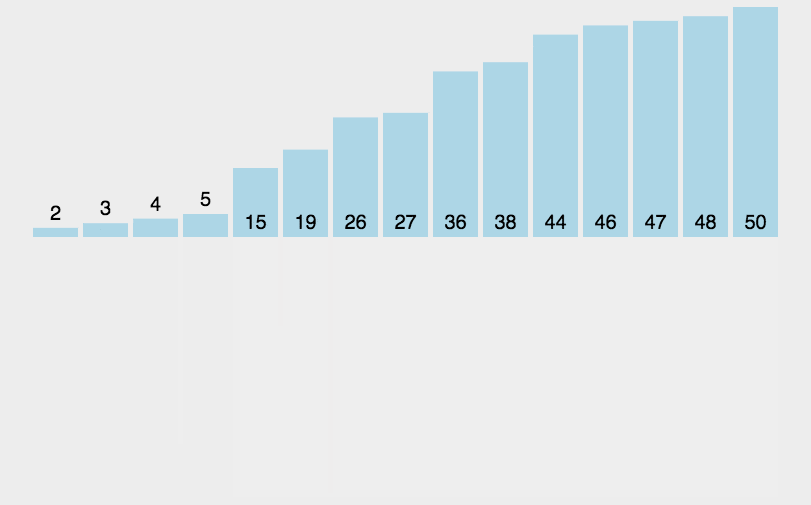
3. Java 代码实现
public class MergeSort implements IArraySort { @Override public int[] sort(int[] sourceArray) throws Exception { // 对 arr 进行拷贝,不改变参数内容 int[] arr = Arrays.copyOf(sourceArray, sourceArray.length); if (arr.length 0 && right.length > 0) { if (left[0] 0) { result[i++] = left[0]; left = Arrays.copyOfRange(left, 1, left.length); } while (right.length > 0) { result[i++] = right[0]; right = Arrays.copyOfRange(right, 1, right.length); } return result; } }
六、快速排序
快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下,排序 n 个项目要 Ο(nlogn) 次比较。在最坏状况下则需要 Ο(n2) 次比较,但这种状况并不常见。事实上,快速排序通常明显比其他 Ο(nlogn) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来。
快速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。
快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看,快速排序应该算是在冒泡排序基础上的递归分治法。
快速排序的名字起的是简单粗暴,因为一听到这个名字你就知道它存在的意义,就是快,而且效率高!它是处理大数据最快的排序算法之一了。虽然 Worst Case 的时间复杂度达到了 O(n²),但是人家就是优秀,在大多数情况下都比平均时间复杂度为 O(n logn) 的排序算法表现要更好,可是这是为什么呢,我也不知道。
快速排序的最坏运行情况是 O(n²),比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn),且 O(nlogn) 记号中隐含的常数因子很小,比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以,对绝大多数顺序性较弱的随机数列而言,快速排序总是优于归并排序。
1. 算法步骤
从数列中挑出一个元素,称为 “基准”(pivot);
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
递归的***部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会退出,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它***的位置去。
2. 动图演示
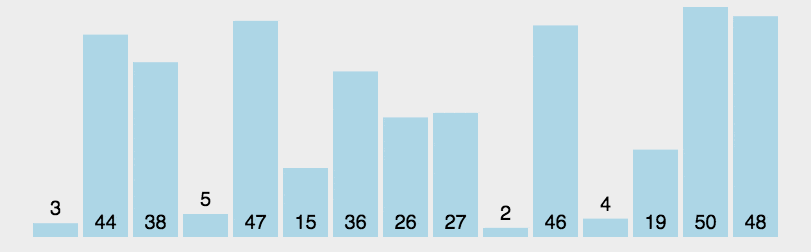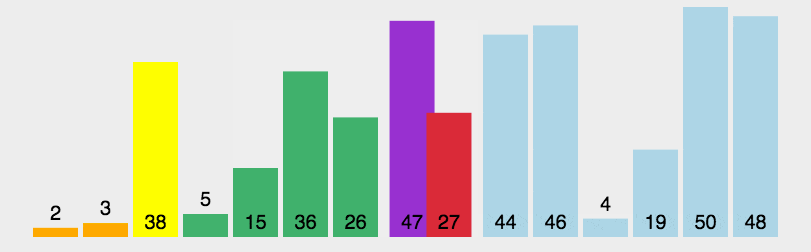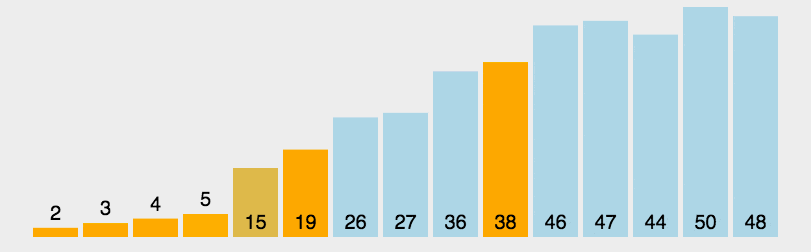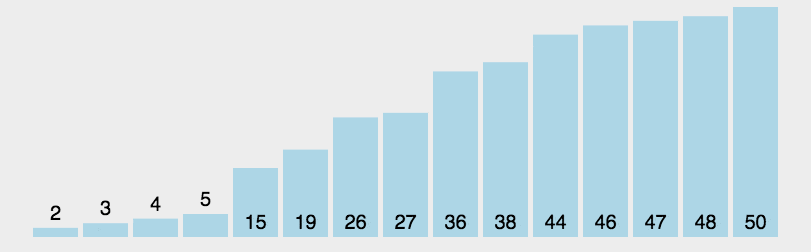
3. Java 代码实现
public class QuickSort implements IArraySort { @Override public int[] sort(int[] sourceArray) throws Exception { // 对 arr 进行拷贝,不改变参数内容 int[] arr = Arrays.copyOf(sourceArray, sourceArray.length); return quickSort(arr, 0, arr.length - 1); } private int[] quickSort(int[] arr, int left, int right) { if (left <p><strong>七、堆排序</strong></p><p>堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:</p><ol class=" list-paddingleft-2">
<li><p>鸿蒙官方战略合作共建——HarmonyOS技术社区</p></li>
<li><p>大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列;</p></li>
<li><p>小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列;</p></li>
</ol><p>堆排序的平均时间复杂度为 Ο(nlogn)。</p><p><strong>1. 算法步骤</strong></p><ol class=" list-paddingleft-2">
<li><p>鸿蒙官方战略合作共建——HarmonyOS技术社区</p></li>
<li><p>创建一个堆 H[0……n-1];</p></li>
<li><p>把堆首(***值)和堆尾互换;</p></li>
<li><p>把堆的尺寸缩小 1,并调用 shift_down(0),目的是把新的数组顶端数据调整到相应位置;</p></li>
<li><p>重复步骤 2,直到堆的尺寸为 1。</p></li>
</ol><p><strong>2. 动图演示</strong></p><center><img src="/static/imghwm/default1.png" data-src="https://img.php.cn/upload/article/000/887/227/168277254995371.gif" class="lazy" alt="Javaコードで古典的なソートアルゴリズムを使用する方法"></center><p><strong>3. Java 代码实现</strong></p><pre class="brush:php;toolbar:false">public class HeapSort implements IArraySort { @Override public int[] sort(int[] sourceArray) throws Exception { // 对 arr 进行拷贝,不改变参数内容 int[] arr = Arrays.copyOf(sourceArray, sourceArray.length); int len = arr.length; buildMaxHeap(arr, len); for (int i = len - 1; i > 0; i--) { swap(arr, 0, i); len--; heapify(arr, 0, len); } return arr; } private void buildMaxHeap(int[] arr, int len) { for (int i = (int) Math.floor(len / 2); i >= 0; i--) { heapify(arr, i, len); } } private void heapify(int[] arr, int i, int len) { int left = 2 * i + 1; int right = 2 * i + 2; int largest = i; if (left arr[largest]) { largest = left; } if (right arr[largest]) { largest = right; } if (largest != i) { swap(arr, i, largest); heapify(arr, largest, len); } } private void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }八、计数排序
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
1. 动图演示
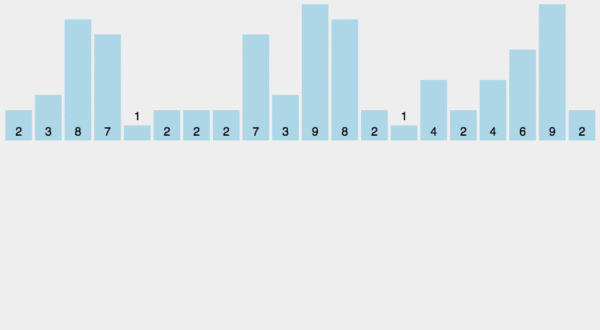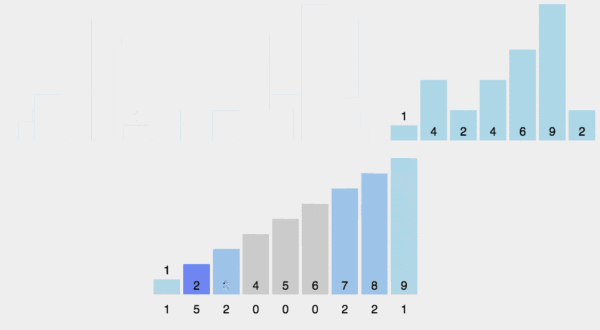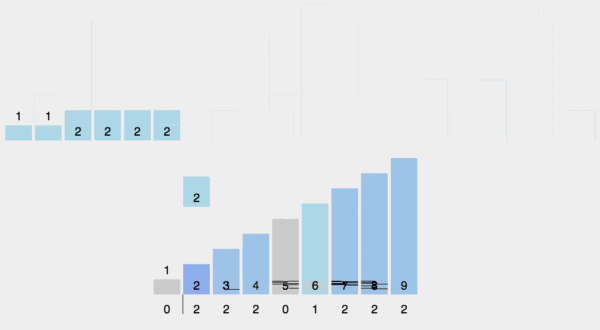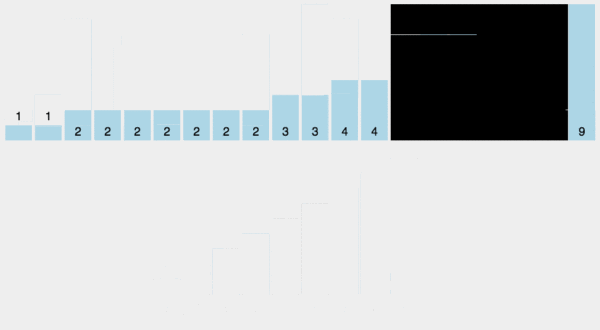
2. Java 代码实现
public class CountingSort implements IArraySort { @Override public int[] sort(int[] sourceArray) throws Exception { // 对 arr 进行拷贝,不改变参数内容 int[] arr = Arrays.copyOf(sourceArray, sourceArray.length); int maxValue = getMaxValue(arr); return countingSort(arr, maxValue); } private int[] countingSort(int[] arr, int maxValue) { int bucketLen = maxValue + 1; int[] bucket = new int[bucketLen]; for (int value : arr) { bucket[value]++; } int sortedIndex = 0; for (int j = 0; j 0) { arr[sortedIndex++] = j; bucket[j]--; } } return arr; } private int getMaxValue(int[] arr) { int maxValue = arr[0]; for (int value : arr) { if (maxValue <p><strong>九、桶排序</strong></p><p>桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效,我们需要做到这两点:</p>
在额外空间充足的情况下,尽量增大桶的数量
使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中
同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。
1. 什么时候最快
当输入的数据可以均匀的分配到每一个桶中。
2. 什么时候最慢
当输入的数据被分配到了同一个桶中。
3. Java 代码实现
public class BucketSort implements IArraySort { private static final InsertSort insertSort = new InsertSort(); @Override public int[] sort(int[] sourceArray) throws Exception { // 对 arr 进行拷贝,不改变参数内容 int[] arr = Arrays.copyOf(sourceArray, sourceArray.length); return bucketSort(arr, 5); } private int[] bucketSort(int[] arr, int bucketSize) throws Exception { if (arr.length == 0) { return arr; } int minValue = arr[0]; int maxValue = arr[0]; for (int value : arr) { if (value maxValue) { maxValue = value; } } int bucketCount = (int) Math.floor((maxValue - minValue) / bucketSize) + 1; int[][] buckets = new int[bucketCount][0]; // 利用映射函数将数据分配到各个桶中 for (int i = 0; i <p><strong>十、基数排序</strong></p><p>基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。</p><p><strong>1. 基数排序 vs 计数排序 vs 桶排序</strong></p><p>基数排序有两种方法:</p><p>这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:</p>
基数排序:根据键值的每位数字来分配桶;
计数排序:每个桶只存储单一键值;
桶排序:每个桶存储一定范围的数值;
2. LSD 基数排序动图演示

3. Java 代码实现
/** * 基数排序 */ public class RadixSort implements IArraySort { @Override public int[] sort(int[] sourceArray) throws Exception { // 对 arr 进行拷贝,不改变参数内容 int[] arr = Arrays.copyOf(sourceArray, sourceArray.length); int maxDigit = getMaxDigit(arr); return radixSort(arr, maxDigit); } /** * 获取***位数 */ private int getMaxDigit(int[] arr) { int maxValue = getMaxValue(arr); return getNumLenght(maxValue); } private int getMaxValue(int[] arr) { int maxValue = arr[0]; for (int value : arr) { if (maxValue 以上がJavaコードで古典的なソートアルゴリズムを使用する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

