Javaで半挿入ソートアルゴリズムを実装する方法

並べ替えアルゴリズムの概要

並べ替えアルゴリズムは、特定のアルゴリズム要素を使用して、次の規則に従って 1 つ以上のデータ セットを処理します。確立されたパターンを再配置します。最終的なシーケンスは、特定のルールに従って表示されます。

並べ替えアルゴリズムでは、安定性と効率性が考慮しなければならないことがよくある問題です。

安定性: 安定性とは、2 つの同一の要素がシーケンス内に同時に出現する場合、特定の並べ替えアルゴリズムの後、並べ替えの前後で 2 つの要素の相対的な位置が変わらないことを意味します。

複雑度分析:

(1) 時間計算量: つまり、シーケンスの初期状態から、ソート アルゴリズムの変換やシフトなどの操作を経て、最終的なソート結果状態に至るまでのプロセス. 費やされた時間の尺度。

(2) 空間計算量: シーケンスの初期状態からソートおよびシフト変換のプロセスを経て最終状態に至るまでに費やされる空間オーバーヘッドです。

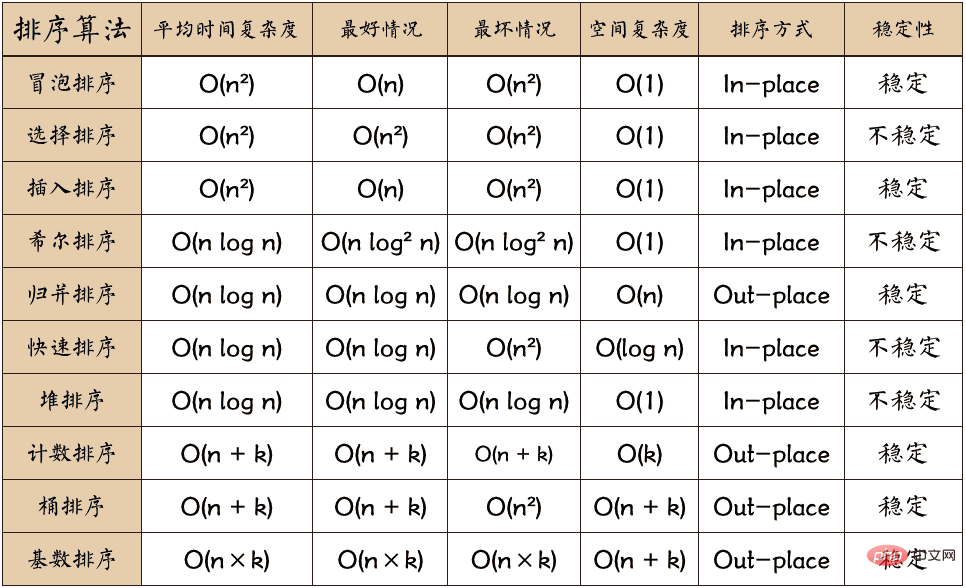
一般的な並べ替えアルゴリズムは次のタイプに分類されます。

半減挿入ソート

原則

半減挿入ソート(Binary Insertion Sort) は、挿入ソート アルゴリズムを改良したものです。以前にソートされたシーケンスに要素を継続的に挿入します。前半はソートされたシーケンスであるため、挿入ポイントを順番に検索する必要はなく、ハーフサーチ方式を使用することで挿入ポイントの検索を高速化できます。

コードの実装

ソートされた配列に新しい要素を挿入するプロセスで、挿入ポイントを探すときに、挿入される領域の最初の要素を a[low] に設定します。要素が a[high] に設定されている場合、挿入される要素は比較の各ラウンドで a[m] と比較されます (m = (low high)/2)。参照要素よりも a[low] から a[m-1] を選択すると、新しい挿入領域になります (つまり、high=m-1)。そうでない場合は、新しい挿入領域として a[m 1] から a[high] を選択します (つまり、a[m-1] を選択します)。 low=m 1) など、 low

つまり、配置された要素の順序特性を利用し、半検索の特性を使用して、挿入する位置をすばやく見つけます。

    // Binary Insertion Sort method    
    private static void binaryInsertSort(int[] array){
       
        for(int i = 1; i < array.length; i++){
           
            int temp = array[i];            
            int low = 0;            
            int high = i - 1;  
           
            while(low <= high){                
                int mid = (low + high) / 2;                
                if(temp < array[mid]){                    
                    high = mid - 1;                
                }else{                    
                    low = mid + 1;
                }       
            }
           
            for(int j = i; j >= low + 1; j--){            
                array[j] = array[j - 1];                                                      
            }       
           
            array[low] = temp;       
        }   
    }

複雑性分析

半挿入ソート アルゴリズムは、安定したソート アルゴリズムです。直接挿入アルゴリズムよりもキーワード間の比較の数が大幅に削減されるため、直接挿入ソートより高速です。高速ですが、レコードの移動数は変わっていないため、半減挿入ソート アルゴリズムの時間計算量は依然として O(n^2) であり、これは直接挿入ソート アルゴリズムと同じです。

時間計算量

最良の場合: O(n)。要素が順方向にソートされている場合、位置は検索やシフトを行わずに、先頭で直接検索されます。

最悪の場合: O(n^2)。要素が逆順に並べ替えられている場合は、毎回データの検索が必要になります。

平均複雑さ: O(n^2)。

空間複雑度: O(1)。主要な情報単位を記録するのに必要な記憶スペースはわずかです。つまり、スペースの複雑さは O(1) です。

例:

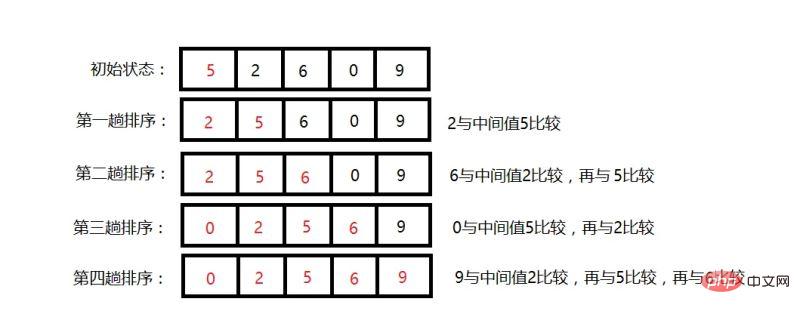
アルゴリズムの実践

アルゴリズムの全体的な考え方は上で説明しました。例を使用してテストしてみましょう直接水をかけてください。

半挿入ソート

問題の説明:

整数配列 nums を与えました。配列を昇順にソートしてください。

例 1:

入力: nums = [5,2,3,1]

出力: [1,2,3,5]

例 2:

入力: nums = [5,1,1,2,0,0]

出力: [0,0,1,1,2,5]

ヒント:

1

-5 * 104 rreee

以上がJavaで半挿入ソートアルゴリズムを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。