Javaで最小スパニングツリーを見つける方法
- WBOY転載
- 2023-04-29 18:58:13694ブラウズ
1 最小スパニング ツリーの概要
スパニング ツリー: 接続されたグラフのスパニング ツリーは、グラフのすべての n 頂点を含む接続されたサブグラフを参照します。ただし、ツリーを形成するには n-1 個のエッジのみが必要です。 n 個の頂点を持つスパニング ツリーには n-1 個のエッジしかありません。スパニング ツリーに別のエッジが追加されると、必ずサイクルが形成されます。
最小スパニング ツリー: 接続されたグラフ内のすべてのスパニング ツリーの中で、すべてのエッジの重みと最小のスパニング ツリーを最小スパニング ツリーと呼びます。
日常生活では、グラフィック構造が最も広く使用されています。例えば、一般的な通信ネットワークの構築ルート選定では、村を頂点とみなして、村間に通信路がある場合は2点間の辺や円弧として数え、2つの村間の通信コストを1つの単位として考えることができます。エッジまたは円弧の重み値。
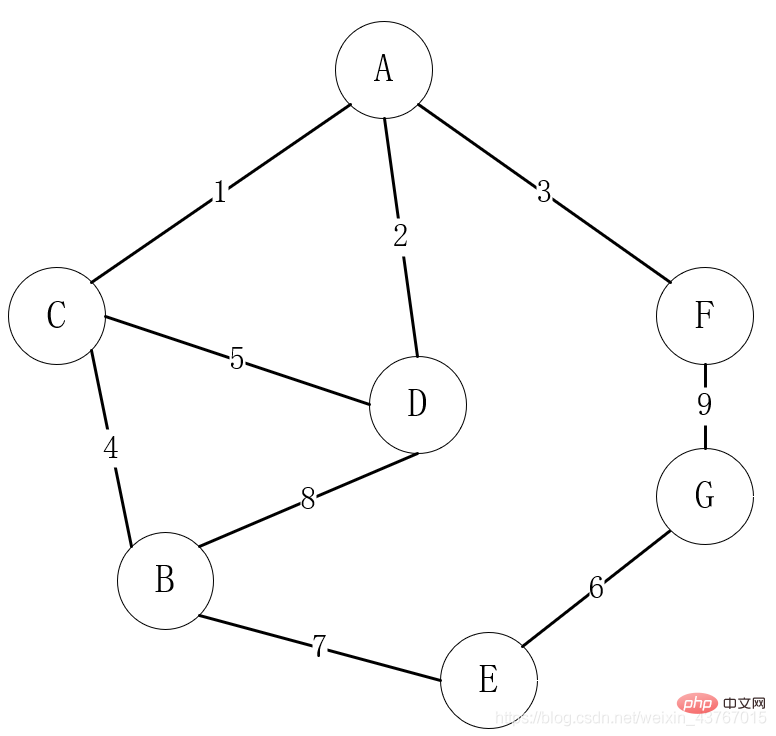
#上の図は、人生における通信ネットワーク構築ルートの選択をグラフ構造にマッピングした例です。頂点は村として機能します。村間に通信パスがある場合、頂点にはエッジがあります。村間の通信を確立するコストはエッジの重みになります。
非常に一般的な要件は、通信できるすべての村が通信する必要があり、通信構築のコストが最小限であることです。結局のところ、資金は「限られている」ため、資金は節約されます。
上記の問題を数学モデルに変換すると、グラフの最小全域木を見つける問題、つまり、接続されているすべての頂点を結び、重みの合計が最小となるルートを選択する問題になります。この問題には多くの解決策がありますが、最も古典的な 2 つのアルゴリズムは、Prim のアルゴリズムと Kruskal のアルゴリズムです。
2 プリムのアルゴリズム (Prim)
2.1 原理
プリムのアルゴリズムは、すべての頂点が接続されていないと仮定して、特定の頂点から開始し、徐々に最小のエッジを見つけます。各頂点に重みを付けて接続し、最小スパニング ツリーを構築します。最小スパニング ツリーを構築するための目標としてポイントを使用します。
具体的な手順は次のとおりです: まず頂点 a をランダムに選択し、頂点 a に接続できるすべての頂点を見つけます。接続する重みの低い頂点を選択します。次に、これら 2 つに接続できるすべての頂点を見つけます。頂点または、頂点の 1 つに接続する重みの低い頂点を選択します。このプロセスを n-1 回繰り返し、そのたびに (最初の頂点に最も短い頂点ではなく) 接続された端の頂点に最も近い頂点を選択して接続します。すべての頂点が接続され、最小スパニング ツリーが構築されるまで。
2.2 ケース分析
このケースは、以下の実装コードのケースに対応します。
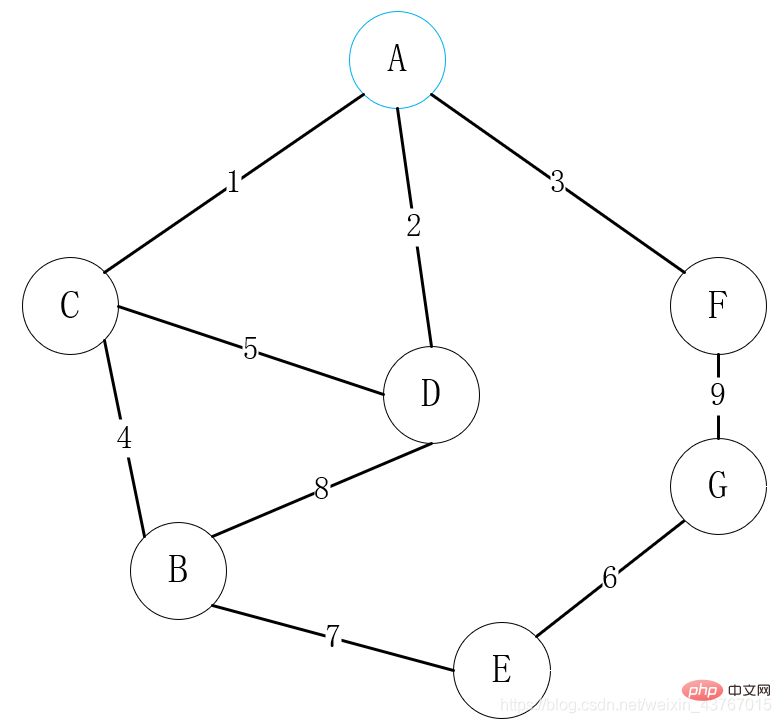
上の図では、まず接続点として頂点 A を選択し、頂点 A がすべての頂点 C、D、F を接続できることを確認し、頂点 A の値が低いものを選択します。重み 頂点が接続されています、ここでは A-C を選択します;
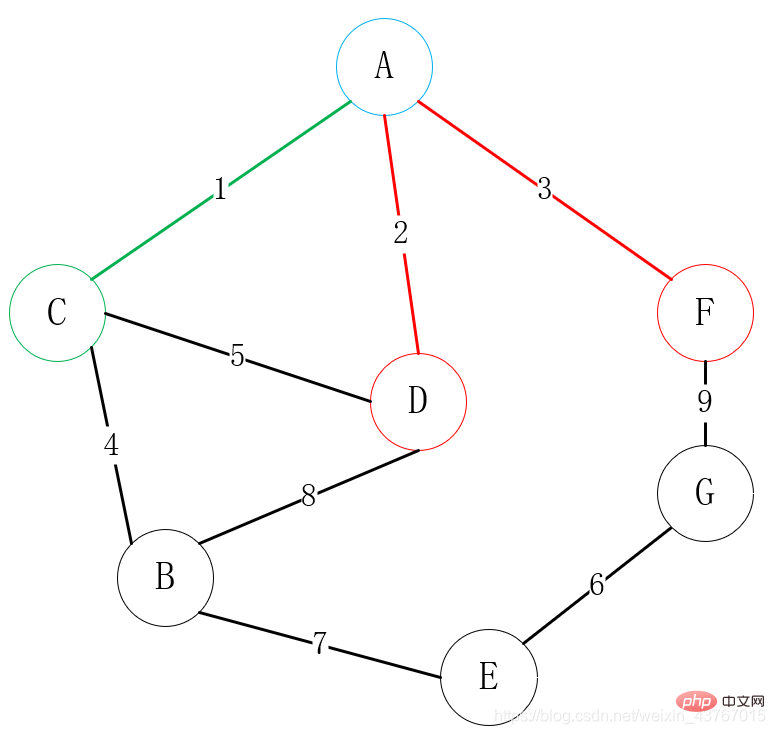
次に、A または C に接続できるすべての頂点を見つけます (接続された点を除く)、B、D、F、a を見つけます。合計 4 つのエッジから選択できます。A-D、A-F、C-B、C-D。重みの低い頂点を選択して、頂点の 1 つに接続します。ここでは、明らかに A-D を選択して接続します。
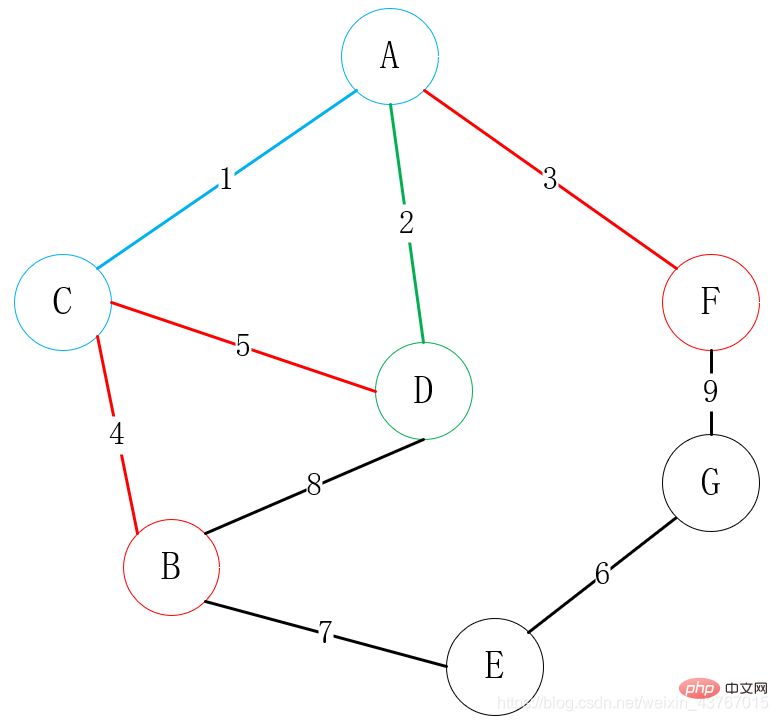
次に、A、C、または D に接続できるすべての頂点 (接続された点を除く) を見つけ、B と F を見つけます。選択できるエッジは 3 つあります。C-B、D-B、A-F、次の頂点を選択します。重みが低く、そのうちの 1 つの頂点が接続されています。ここでは明らかに A-F 接続が選択されています。
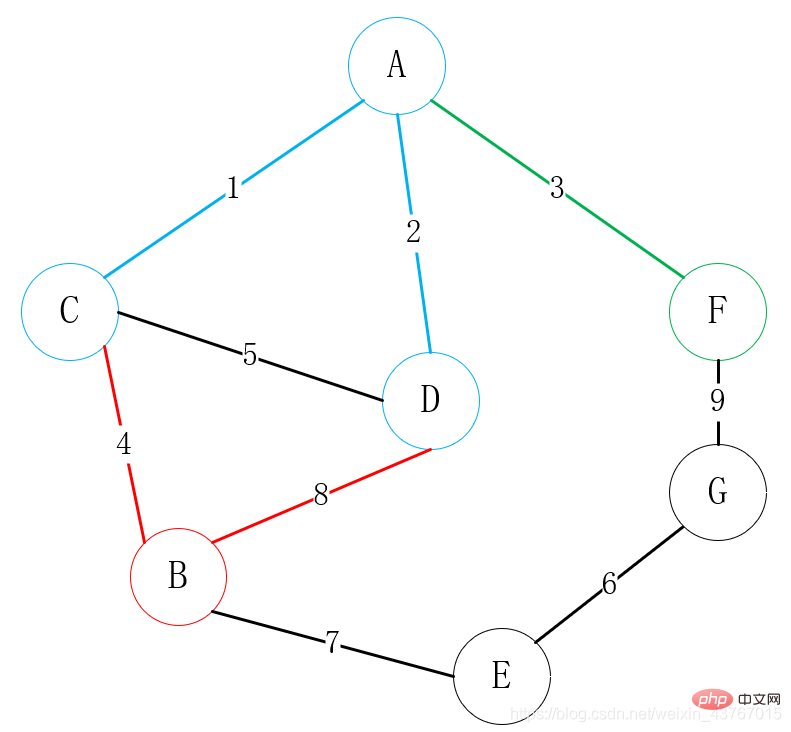
次に、A または C または D または F に接続できるすべての頂点を探します。 (接続点を除く)、 B 、 G を見つけます。選択できるエッジは合計 3 つあります。 C-B、D-B、F-G です。頂点の 1 つに接続するために、重みの低い頂点を選択してください。ここでは明らかに C-B 接続が選択されています。 ;
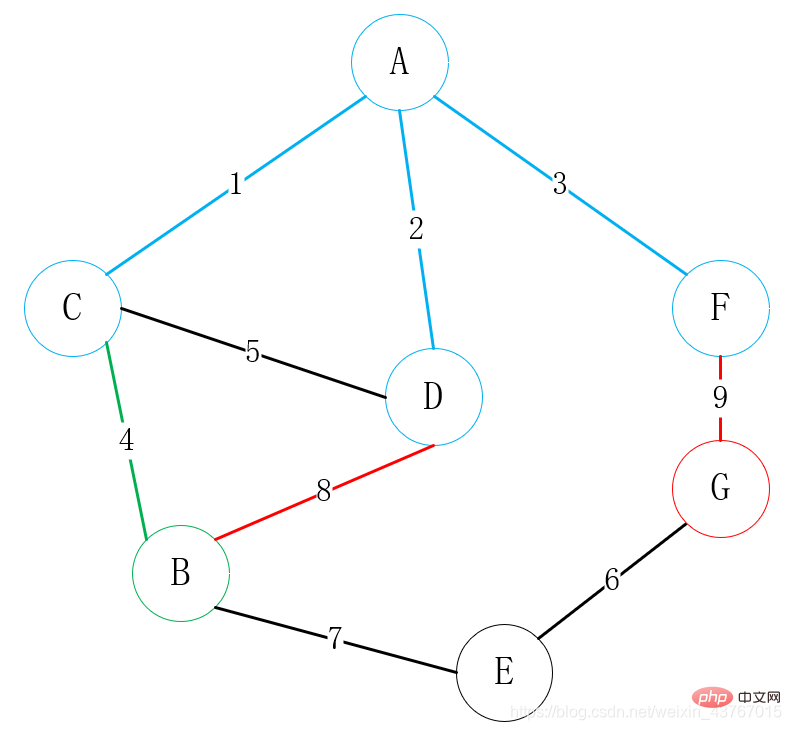
次に、A または C または D または F または B に接続できるすべての頂点を見つけて (接続された点を除く)、E と G を見つけます。接続するエッジは 2 つあります。 B-E、F-G から選択し、重みの低いものを選択します 頂点は頂点の 1 つに接続されます ここでは、明らかに B-E 接続が選択されています;
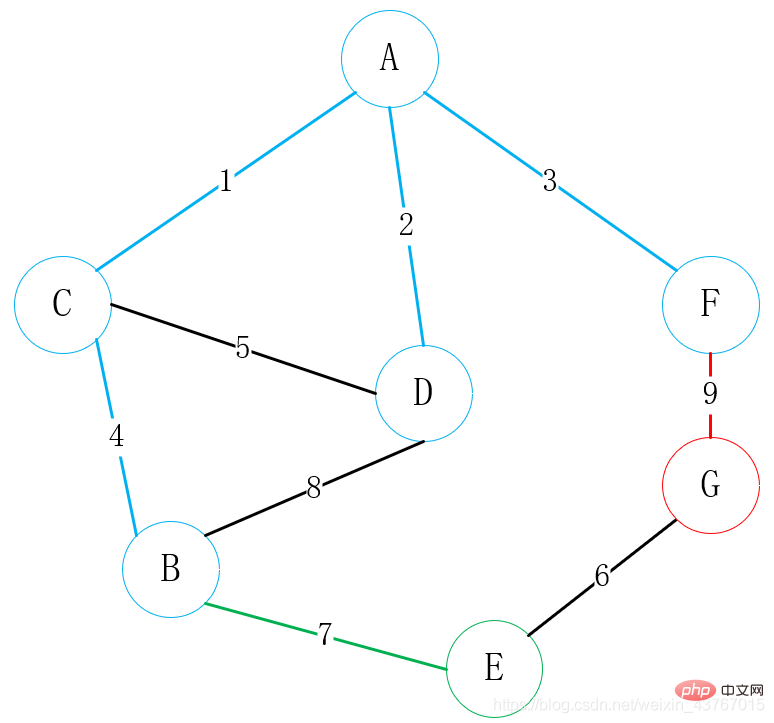
次に、次を見つけますA または C または D または F または B または E (接続された点を除く) に接続できるすべての頂点、G を見つけます。選択できるエッジは 2 つあります。E-G、F-G、重みの低い頂点を選択して 1 つに接続します。頂点の, ここでは明らかに E-G 接続を選択します;
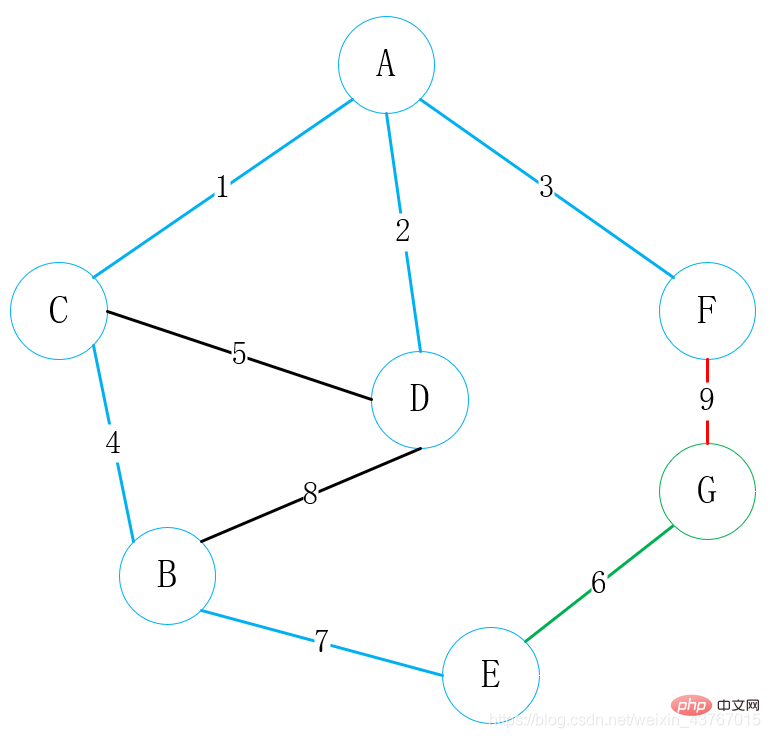
すべての頂点が接続されています. この時点で、最小スパニング ツリーが構築されており、最小重みは 23 です。
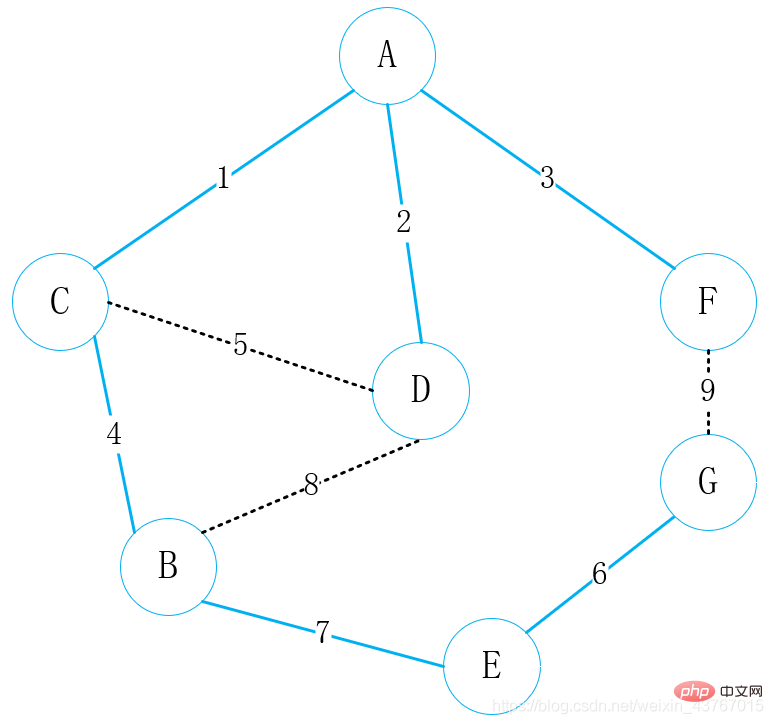
3 クラスカル アルゴリズム (Kruskal)
3.1 原理
クラスカル アルゴリズム (Kruskal) は、エッジの重みに基づいて増加する方法で最小スパニング ツリーを徐々に確立します。これは、エッジをターゲットとして使用します。最小スパニングツリーを構築します。
具体的な手順は次のとおりです。重み付きグラフの各頂点をフォレストとして扱い、グラフ内の各隣接エッジの重みを昇順に配置し、配置された隣接エッジ テーブルから抽出します。最小の重みを付け、エッジの開始頂点と終了頂点を書き込み、頂点を接続してフォレストをツリーに形成します。次に、開始頂点と終了頂点の隣接するエッジを読み取り、最初に小さい重みを持つ隣接エッジを抽出し、接続を続けます。森を形成する頂点を配置し、ツリーを作成します。隣接するエッジを追加するための要件は、グラフに追加される隣接するエッジがサイクル (リング) を形成しないことです。これは、n-1 個のエッジが追加されるまで繰り返されます。この時点で、最小のスパニングツリーが構築されます。
3.2 ケース分析
このケースは、以下の実装コードのケースに対応します。従来のクラスカル アルゴリズムのプロセスは次のとおりです:
最初にエッジ セット配列を取得し、reduceソートの場合、コード内でソートソートを直接使用するか、ヒープソートを自分で実装することもできます。ソート後の結果は次のとおりです:
Edge{from=A, to=C 、weight=1 }
Edge{from=D, to=A,weight=2}
Edge{from=A, to=F,weight=3}
Edge{from=B, to= C、ウェイト= 4}
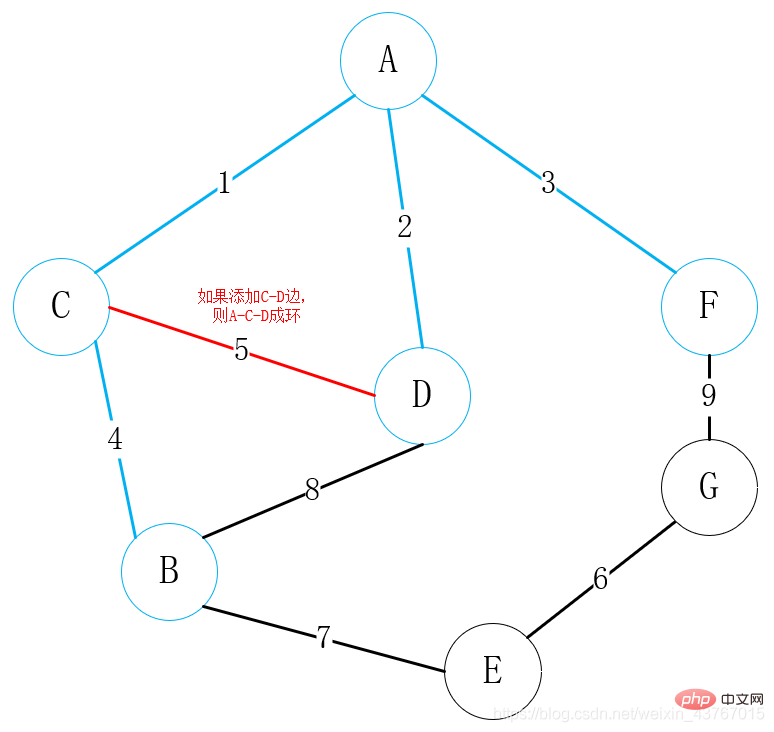
エッジ{from=C, to=D, ウェイト=5}
エッジ{from=E, to=G, ウェイト=6}
エッジ{from=E, to =B、ウェイト =7}
エッジ{from=D、to=B、ウェイト=8}
エッジ{from=F、to=G、ウェイト=9}
1番目のエッジA-Cを取り出すループ、見つかった最小全域木と循環しないと判断し、重みの和を1増やして続行;
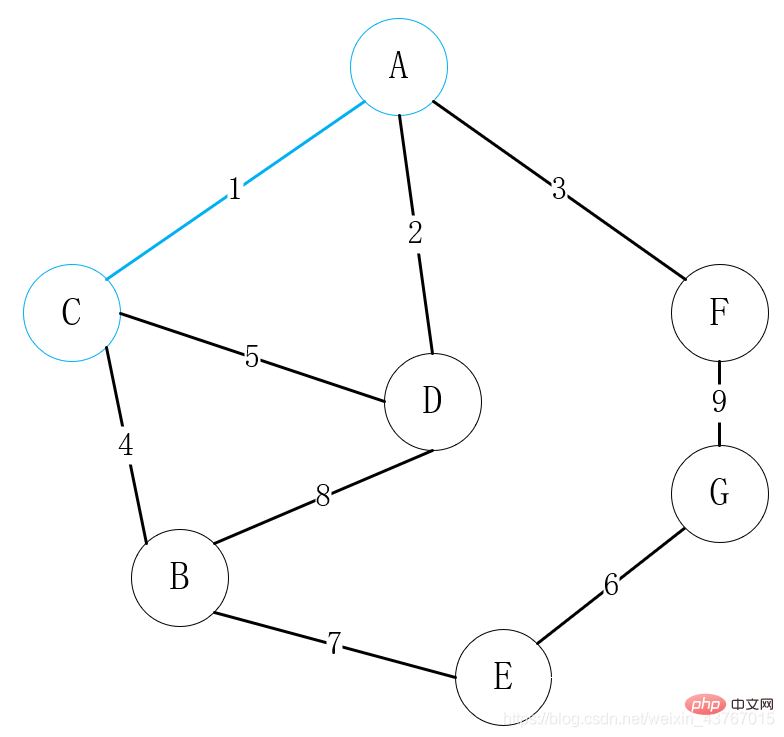
2 番目のエッジ D-A をループアウトし、判定し、見つかった最小全域木は循環を形成しません。合計の重み値は 2 増加して継続します。
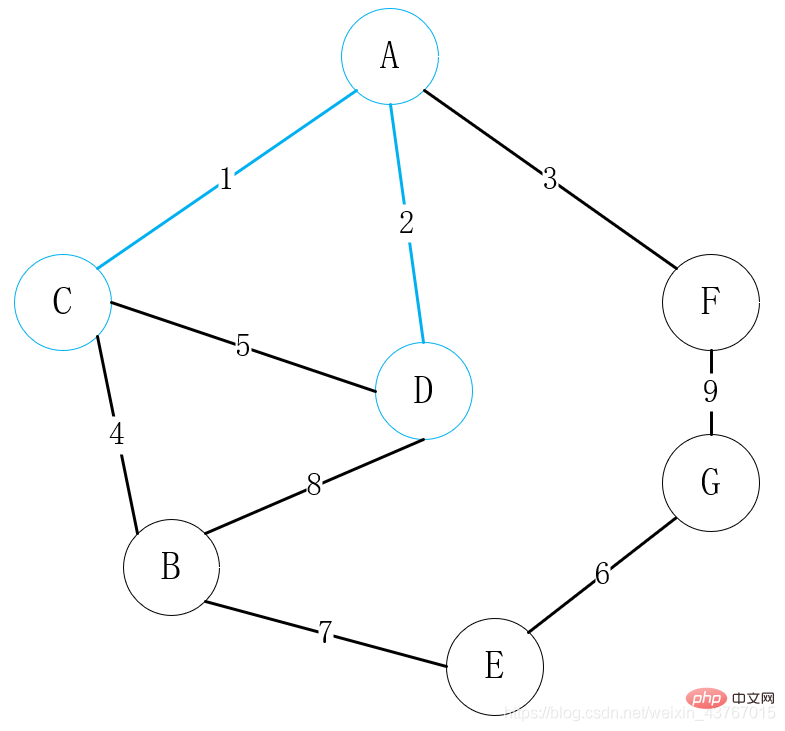
ループアウト3 番目のエッジ A ～ F を検出し、見つかった最小全域木と同じであると判断します。サイクルは形成されず、合計の重み値は 3 増加します。続行;
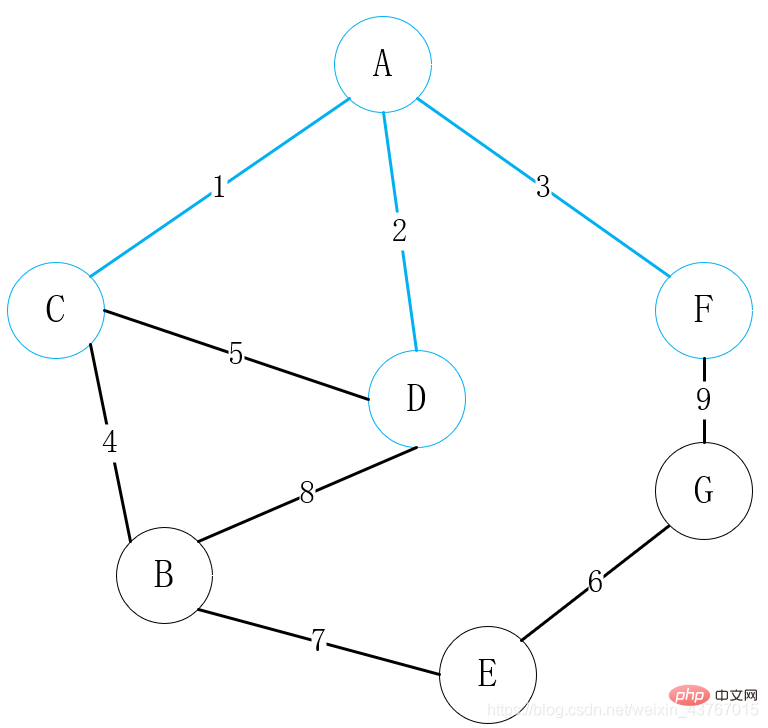
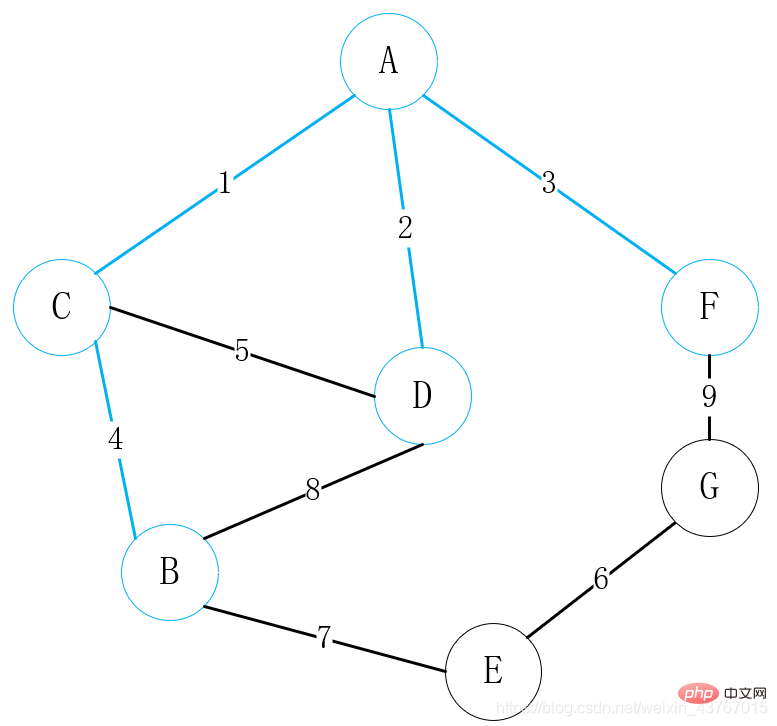
# 6 番目のエッジ E-G をループアウトし、見つかった最小全域木と循環しないと判断し、合計の重みを 6 増やして続行します;
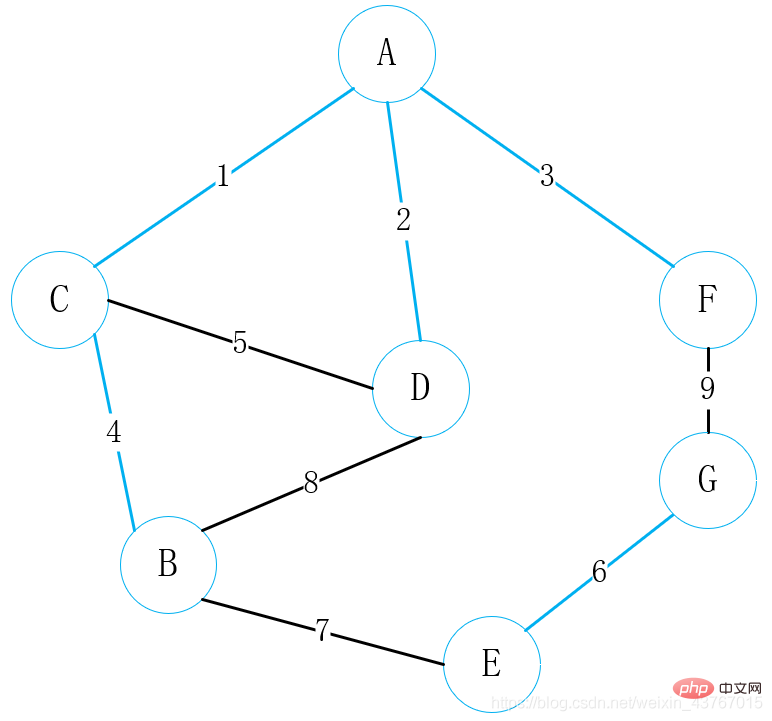をループアウトします。 7 番目のエッジ E-B、見つかった最小スパニング ツリーとサイクルを形成しないと判断し、合計の重みを 7 増やして続行;
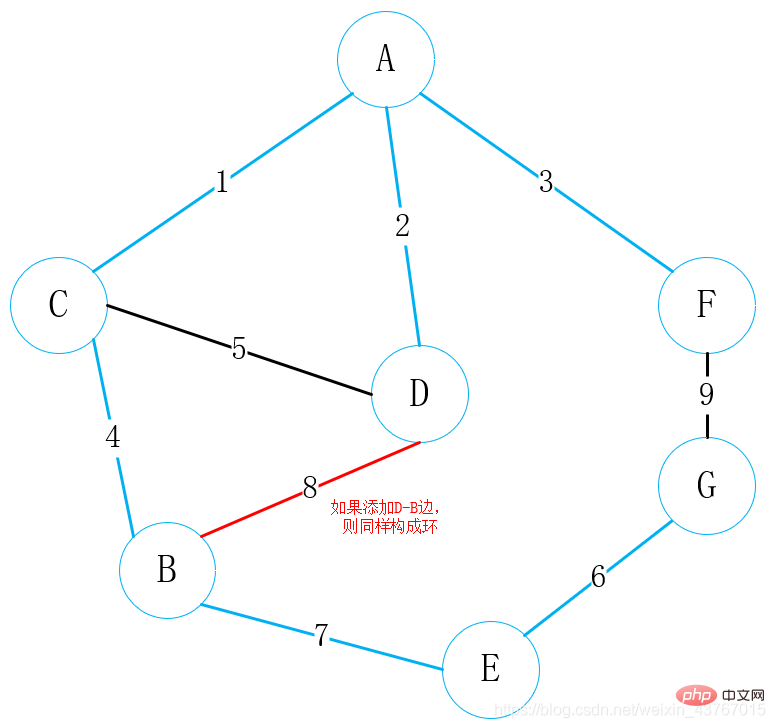
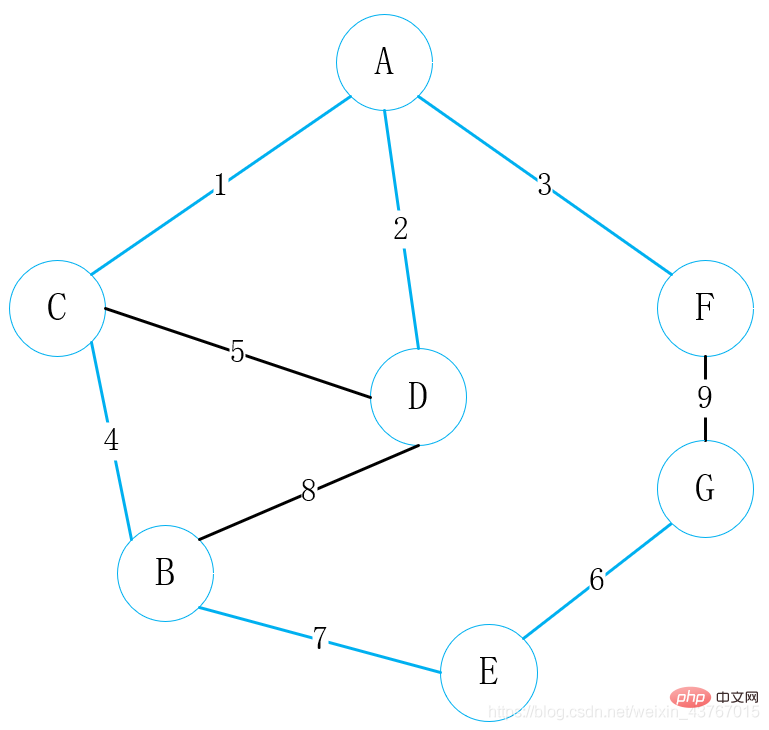をループアウトします。 8番目のエッジD-B、見つかった最小スパニングツリーでループを形成すると判断し、このエッジを破棄して続行;
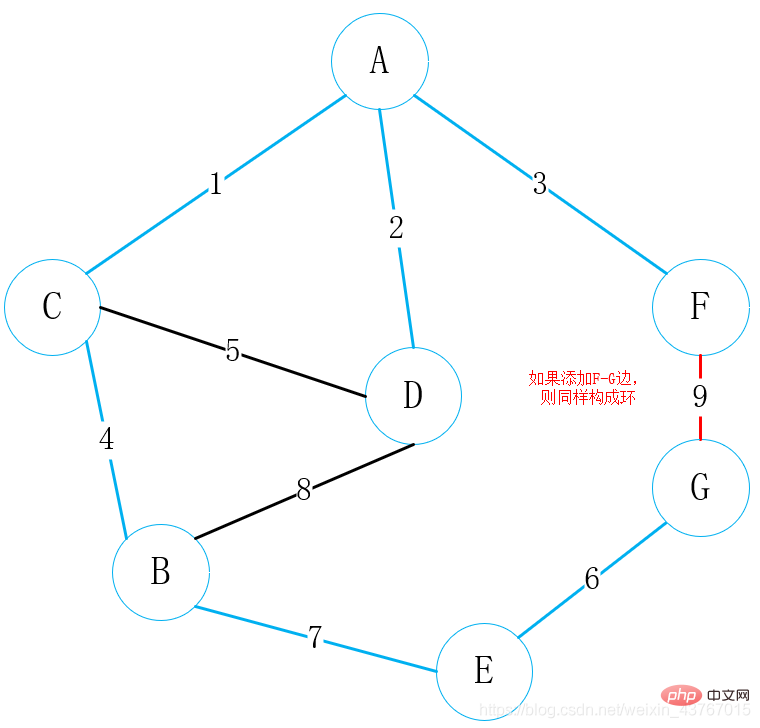
9番目のエッジF-Gをループアウト、見つかった最小スパニングツリーでサイクルを形成すると判断し、エッジを破棄して継続します;
今回でループは終了し、その後最小スパニング ツリーも見つかりました。最小スパニング ツリーの重みの合計は 23 です。
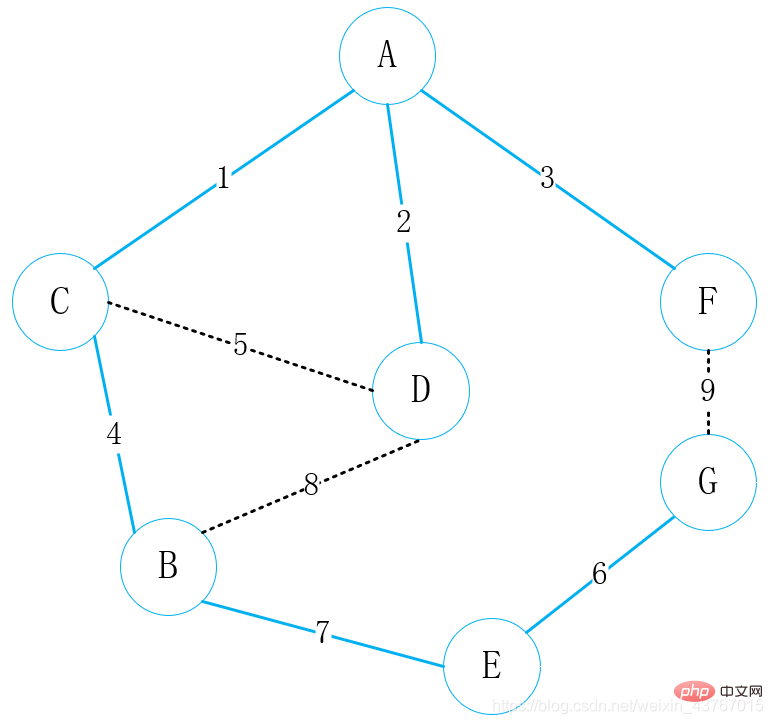上記の手順では、サイクルが形成されているかどうかを判断することが重要です。通常のアプローチは、見つかった最小スパニング ツリーの頂点を (次から) 並べ替えることです。始点から終点まで)、新しいエッジが追加されるたびに、新しく追加されたエッジの始点と終点を使用して最小の二分木を見つけます。ソートされた終点が同じである場合は、それを意味します。最小スパニング ツリーとこのエッジがサイクルを形成しますが、それ以外の場合はサイクルを形成せず、ソートの終了点を更新します。
4 隣接行列重み付きグラフの実装
ここでの実装では、隣接行列に基づいて無向重み付きグラフを実装し、深さ優先トラバーサル メソッドと幅優先トラバーサル メソッドを提供するクラスを構築できます。エッジ取得を提供します。 set array メソッドには、最小スパニング ツリーを見つけるための 2 つのメソッド、Prim と Kruskal が用意されています。
/**
* 无向加权图邻接矩阵实现
* {@link MatrixPrimAndKruskal#MatrixPrimAndKruskal(E[], Edge[])} 构建无向加权图
* {@link MatrixPrimAndKruskal#DFS()} 深度优先遍历无向加权图
* {@link MatrixPrimAndKruskal#BFS()} 广度优先遍历无向加权图
* {@link MatrixPrimAndKruskal#toString()} 输出无向加权图
* {@link MatrixPrimAndKruskal#prim()} Prim算法实现最小生成树
* {@link MatrixPrimAndKruskal#kruskal()} Kruskal算法实现最小生成树
* {@link MatrixPrimAndKruskal#kruskalAndPrim()} Kruskal算法结合Prim算法实现最小生成树
* {@link MatrixPrimAndKruskal#getEdges()} 获取边集数组
*
* @author lx
* @date 2020/5/14 18:13
*/
public class MatrixPrimAndKruskal<E> {
/**
* 顶点数组
*/
private Object[] vertexs;
/**
* 邻接矩阵
*/
private int[][] matrix;
/**
*
*/
private Edge<E>[] edges;
/**
* 由于是加权图,这里设置一个边的权值上限,任何边的最大权值不能大于等于该值，在实际应用中，该值应该根据实际情况确定
*/
private static final int NO_EDGE = 99;
/**
* 边对象,具有权值,在构建加权无向图时使用
*/
private static class Edge<E> {
private E from;
private E to;
private int weight;
public Edge(E from, E to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
@Override
public String toString() {
return "Edge{" +
"from=" + from +
", to=" + to +
", weight=" + weight +
'}';
}
}
/**
* 创建无向加权图
*
* @param vertexs 顶点数组
* @param edges 边对象数组
*/
public MatrixPrimAndKruskal(Object[] vertexs, Edge<E>[] edges) {
//初始化边数组
this.edges = edges;
// 初始化顶点数组,并添加顶点
this.vertexs = Arrays.copyOf(vertexs, vertexs.length);
// 初始化边矩阵,并预先填充边信息
this.matrix = new int[vertexs.length][vertexs.length];
for (int i = 0; i < vertexs.length; i++) {
for (int j = 0; j < vertexs.length; j++) {
if (i == j) {
this.matrix[i][j] = 0;
} else {
this.matrix[i][j] = NO_EDGE;
}
}
}
for (Edge<E> edge : edges) {
// 读取一条边的起始顶点和结束顶点索引值
int p1 = getPosition(edge.from);
int p2 = getPosition(edge.to);
//对称的两个点位都置为edge.weight,无向图可以看作相互可达的有向图
this.matrix[p1][p2] = edge.weight;
this.matrix[p2][p1] = edge.weight;
}
}
/**
* 获取某条边的某个顶点所在顶点数组的索引位置
*
* @param e 顶点的值
* @return 所在顶点数组的索引位置, 或者-1 - 表示不存在
*/
private int getPosition(E e) {
for (int i = 0; i < vertexs.length; i++) {
if (vertexs[i] == e) {
return i;
}
}
return -1;
}
/**
* 深度优先搜索遍历图,类似于树的前序遍历,
*/
public void DFS() {
//新建顶点访问标记数组,对应每个索引对应相同索引的顶点数组中的顶点
boolean[] visited = new boolean[vertexs.length];
//初始化所有顶点都没有被访问
for (int i = 0; i < vertexs.length; i++) {
visited[i] = false;
}
System.out.println("DFS: ");
for (int i = 0; i < vertexs.length; i++) {
if (!visited[i]) {
DFS(i, visited);
}
}
System.out.println();
}
/**
* 深度优先搜索遍历图的递归实现,类似于树的先序遍历
* 因此模仿树的先序遍历,同样借用栈结构,这里使用的是方法的递归,隐式的借用栈
*
* @param i 顶点索引
* @param visited 访问标志数组
*/
private void DFS(int i, boolean[] visited) {
visited[i] = true;
System.out.print(vertexs[i] + " ");
// 遍历该顶点的所有邻接点。若该邻接点是没有访问过，那么继续递归遍历领接点
for (int w = firstVertex(i); w >= 0; w = nextVertex(i, w)) {
if (!visited[w]) {
DFS(w, visited);
}
}
}
/**
* 广度优先搜索图,类似于树的层序遍历
* 因此模仿树的层序遍历,同样借用队列结构
*/
public void BFS() {
// 辅组队列
Queue<Integer> indexLinkedList = new LinkedList<>();
//新建顶点访问标记数组,对应每个索引对应相同索引的顶点数组中的顶点
boolean[] visited = new boolean[vertexs.length];
for (int i = 0; i < vertexs.length; i++) {
visited[i] = false;
}
System.out.println("BFS: ");
for (int i = 0; i < vertexs.length; i++) {
if (!visited[i]) {
visited[i] = true;
System.out.print(vertexs[i] + " ");
indexLinkedList.add(i);
}
if (!indexLinkedList.isEmpty()) {
//j索引出队列
Integer j = indexLinkedList.poll();
//继续访问j的邻接点
for (int k = firstVertex(j); k >= 0; k = nextVertex(j, k)) {
if (!visited[k]) {
visited[k] = true;
System.out.print(vertexs[k] + " ");
//继续入队列
indexLinkedList.add(k);
}
}
}
}
System.out.println();
}
/**
* 返回顶点v的第一个邻接顶点的索引，失败则返回-1
*
* @param v 顶点v在数组中的索引
* @return 返回顶点v的第一个邻接顶点的索引，失败则返回-1
*/
private int firstVertex(int v) {
//如果索引超出范围,则返回-1
if (v < 0 || v > (vertexs.length - 1)) {
return -1;
}
/*根据邻接矩阵的规律:顶点索引v对应着边二维矩阵的matrix[v][i]一行记录
* 从i=0开始*/
for (int i = 0; i < vertexs.length; i++) {
if (matrix[v][i] != 0 && matrix[v][i] != NO_EDGE) {
return i;
}
}
return -1;
}
/**
* 返回顶点v相对于w的下一个邻接顶点的索引，失败则返回-1
*
* @param v 顶点索引
* @param w 第一个邻接点索引
* @return 返回顶点v相对于w的下一个邻接顶点的索引，失败则返回-1
*/
private int nextVertex(int v, int w) {
//如果索引超出范围,则返回-1
if (v < 0 || v > (vertexs.length - 1) || w < 0 || w > (vertexs.length - 1)) {
return -1;
}
/*根据邻接矩阵的规律:顶点索引v对应着边二维矩阵的matrix[v][i]一行记录
* 由于邻接点w的索引已经获取了,所以从i=w+1开始寻找*/
for (int i = w + 1; i < vertexs.length; i++) {
if (matrix[v][i] != 0 && matrix[v][i] != NO_EDGE) {
return i;
}
}
return -1;
}
/**
* 输出图
*
* @return 输出图字符串
*/
@Override
public String toString() {
StringBuilder stringBuilder = new StringBuilder();
for (int i = 0; i < vertexs.length; i++) {
for (int j = 0; j < vertexs.length; j++) {
stringBuilder.append(matrix[i][j]).append("\t");
}
stringBuilder.append("\n");
}
return stringBuilder.toString();
}
/**
* Prim算法求最小生成树
*/
public void prim() {
System.out.println("prim: ");
//对应节点应该被连接的前驱节点,用来输出
//默认为0,即前驱结点为第一个节点
int[] mid = new int[matrix.length];
//如果某顶点作为末端顶点被连接，对应位置应该为true
//第一个顶点默认被连接
boolean[] connected = new boolean[matrix.length];
connected[0] = true;
//存储未连接顶点到已连接顶点的最短距离(最小权)
int[] dis = new int[matrix.length];
//首先将矩阵第一行即其他顶点到0索引顶点的权值拷贝进去
System.arraycopy(matrix[0], 0, dis, 0, matrix.length);
//存储路径长度
int sum = 0;
//最小权值
int min;
/*默认第一个顶点已经找到了,因此最多还要需要大循环n-1次*/
for (int k = 1; k < matrix.length; k++) {
min = NO_EDGE;
//最小权值的顶点的索引
int minIndex = 0;
/*寻找权值最小的且未被连接的顶点索引*/
for (int i = 1; i < matrix.length; i++) {
//排除已连接的顶点,排除权值等于0的值,这里权值等于0表示已生成的最小生成树的顶点都未能与该顶点连接
if (!connected[i] && dis[i] != 0 && dis[i] < min) {
min = dis[i];
minIndex = i;
}
}
//如果没找到,那么该图可能不是连通图,直接返回了,此时最小生成树没啥意义
if (minIndex == 0) {
return;
}
//权值和增加
sum += min;
//该新连接顶点对应的索引值变成true,表示已被连接,后续判断时跳过该顶点
connected[minIndex] = true;
//输出对应的前驱顶点到该最小顶点的权值
System.out.println(vertexs[mid[minIndex]] + " ---> " + vertexs[minIndex] + " 权值:" + min);
/*在新顶点minIndex加入之前的其他所有顶点到连接顶点最小的权值已经计算过了
因此只需要更新其他未连接顶点到新连接顶点minIndex是否还有更短的权值,有的话就更新找到距离已连接的顶点权最小的顶点*/
for (int i = 1; i < matrix.length; i++) {
//如果该顶点未连接
if (!connected[i]) {
/*如果新顶点到未连接顶点i的权值不为0,并且比原始顶点到未连接顶点i的权值还要小,那么更新对应位置的最小权值*/
if (matrix[minIndex][i] != 0 && dis[i] > matrix[minIndex][i]) {
//更新最小权值
dis[i] = matrix[minIndex][i];
//更新前驱节点索引为新加入节点索引
mid[i] = minIndex;
}
}
}
}
System.out.println("sum: " + sum);
}
/**
* Kruskal算法求最小生成树传统实现,要求知道边集数组,和顶点数组
*/
public void kruskal() {
System.out.println("Kruskal: ");
//由于创建图的时候保存了边集数组,这里直接使用就行了
//Edge[] edges = getEdges();
//this.edges=edges;
//对边集数组进行排序
Arrays.sort(this.edges, Comparator.comparingInt(o -> o.weight));
// 用于保存已有最小生成树中每个顶点在该最小树中的最终终点的索引
int[] vends = new int[this.edges.length];
//能够知道终点索引范围是[0,this.edges.length-1],因此填充edges.length表示没有终点
Arrays.fill(vends, this.edges.length);
int sum = 0;
for (Edge<E> edge : this.edges) {
// 获取第i条边的起点索引from
int from = getPosition(edge.from);
// 获取第i条边的终点索引to
int to = getPosition(edge.to);
// 获取顶点from在"已有的最小生成树"中的终点
int m = getEndIndex(vends, from);
// 获取顶点to在"已有的最小生成树"中的终点
int n = getEndIndex(vends, to);
// 如果m!=n，意味着没有形成环路,则可以添加,否则直接跳过,进行下一条边的判断
if (m != n) {
//添加设置原始终点索引m在已有的最小生成树中的终点为n
vends[m] = n;
System.out.println(vertexs[from] + " ---> " + vertexs[to] + " 权值:" + edge.weight);
sum += edge.weight;
}
}
System.out.println("sum: " + sum);
//System.out.println(Arrays.toString(this.edges));
}
/**
* 获取顶点索引i的终点如果没有终点则返回顶点索引本身
*
* @param vends 顶点在最小生成树中的终点
* @param i 顶点索引
* @return 顶点索引i的终点如果没有终点则返回顶点索引本身
*/
private int getEndIndex(int[] vends, int i) {
//这里使用循环查找的逻辑,寻找的是最终的终点
while (vends[i] != this.edges.length) {
i = vends[i];
}
return i;
}
/**
* 如果没有现成的边集数组，那么根据邻接矩阵结构获取图中的边集数组
*
* @return 图的边集数组
*/
private Edge[] getEdges() {
List<Edge> edges = new ArrayList<>();
/*遍历矩阵数组 只需要遍历一半就行了*/
for (int i = 0; i < vertexs.length; i++) {
for (int j = i + 1; j < vertexs.length; j++) {
//如果存在边
if (matrix[i][j] != NO_EDGE && matrix[i][j] != 0) {
edges.add(new Edge<>(vertexs[i], vertexs[j], matrix[i][j]));
//edges[index++] = new Edge(vertexs[i], vertexs[j], matrix[i][j]);
}
}
}
return edges.toArray(new Edge[0]);
}
/**
* Kruskal结合Prim算法.不需要知道边集,只需要矩阵数组,和顶点数组
* 同样是求最小权值的边,但是有一个默认起点顶点,该起点可以是要求[0,顶点数量-1]之间的任意值，同时查找最小权的边。
* 可能会有Bug,目前未发现
*/
public void kruskalAndPrim() {
System.out.println("kruskalAndPrim: ");
//已经找到的边携带的顶点对应的索引将变为true,其余未找到边对应的顶点将是false
boolean[] connected = new boolean[matrix.length];
//这里选择第一个顶点为起点,表示以该顶点开始寻找包含该顶点的最小边
connected[0] = true;
int sum = 0, n1 = 0, n2 = 0;
//最小权值
int min;
while (true) {
min = NO_EDGE;
/*找出所有带有已找到顶点的边中,最小权值的边,只需要寻找对称矩阵的一半即可*/
//第一维
for (int i = 0; i < matrix.length; i++) {
//第二维
for (int j = i + 1; j < matrix.length; j++) {
//排除等于0的,排除两个顶点都找到了的,这里实际上已经隐含了排除环的逻辑,如果某条边的两个顶点都找到了,那么如果算上该条边,肯定会形成环
//寻找剩下的最小的权值的边
if (matrix[i][j] != 0 && connected[i] != connected[j] && matrix[i][j] < min) {
min = matrix[i][j];
n1 = i;
n2 = j;
}
}
}
//如果没找到最小权值,该图可能不是连通图,或者已经寻找完毕,直接返回
if (min == NO_EDGE) {
System.out.println(" sum:" + sum);
return;
}
//已经找到的边对应的两个顶点都置为true
connected[n1] = true;
connected[n2] = true;
//输出找到的边和最小权值
System.out.println(vertexs[n1] + " ---> " + vertexs[n2] + " 权值:" + min);
sum += min;
}
}
public static void main(String[] args) {
//顶点数组
Character[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
//边数组,加权值
Edge[] edges = {
new Edge<>('A', 'C', 1),
new Edge<>('D', 'A', 2),
new Edge<>('A', 'F', 3),
new Edge<>('B', 'C', 4),
new Edge<>('C', 'D', 5),
new Edge<>('E', 'G', 6),
new Edge<>('E', 'B', 7),
new Edge<>('D', 'B', 8),
new Edge<>('F', 'G', 9)};
//构建图
MatrixPrimAndKruskal<Character> matrixPrimAndKruskal = new MatrixPrimAndKruskal<Character>(vexs, edges);
//输出图
System.out.println(matrixPrimAndKruskal);
//深度优先遍历
matrixPrimAndKruskal.DFS();
//广度优先遍历
matrixPrimAndKruskal.BFS();
//Prim算法输出最小生成树
matrixPrimAndKruskal.prim();
//Kruskal算法输出最小生成树
matrixPrimAndKruskal.kruskal();
//Kruskal算法结合Prim算法输出最小生成树,可能会有Bug,目前未发现
matrixPrimAndKruskal.kruskalAndPrim();
//获取边集数组
Edge[] edges1 = matrixPrimAndKruskal.getEdges();
System.out.println(Arrays.toString(edges1));
}
}5 隣接リストの重み付けグラフの実装
ここでの実装では、隣接リストに基づいて無向重み付けグラフを実装するクラスを構築でき、深さ優先トラバーサルと幅優先のメソッドを提供します。エッジ セット アレイ メソッドでは、最小スパニング ツリーを見つけるための 2 つのメソッド、Prim と Kruskal が提供されます。
rree以上がJavaで最小スパニングツリーを見つける方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。