Python は 8 つの確率分布公式とデータ視覚化チュートリアルを実装します

確率と統計の知識はデータ サイエンスと機械学習の中核であり、データを効果的に収集、レビュー、分析するには統計と確率の知識が必要です。

現実世界には、統計的な性質を持つ現象 (気象データ、販売データ、財務データなど) がいくつかあります。これは、場合によっては、データの特性を記述する数学関数を通じて自然をシミュレートするのに役立つ方法を開発できたことを意味します。 「確率分布は、実験において考えられるさまざまな結果の発生確率を与える数学関数です。」 データの分布を理解することは、私たちの周囲の世界をより適切にモデル化するのに役立ちます。これは、さまざまな結果の可能性を判断したり、イベントの変動性を推定したりするのに役立ちます。これらすべてにより、さまざまな確率分布を理解することは、データ サイエンスと機械学習において非常に価値のあるものになります。 一様分布最も直接的な分布は一様分布です。一様分布は、すべての結果が等しい可能性を持つ確率分布です。たとえば、公平なサイコロを振った場合、任意の数字が出る確率は 1/6 です。これは離散一様分布です。しかし、すべての一様分布が離散的であるわけではなく、連続的であることもあります。指定された範囲内の任意の実数値を取ることができます。 a と b の間の連続一様分布の確率密度関数 (PDF) は次のとおりです。Python でエンコードする方法を見てみましょう:

import numpy as np
import matplotlib.pyplot as plt 
from scipy import stats 
 
# for continuous
a = 0 
b = 50 
size = 5000 
 
X_continuous = np.linspace(a, b, size) 
continuous_uniform = stats.uniform(loc=a, scale=b) 
continuous_uniform_pdf = continuous_uniform.pdf(X_continuous) 
 
# for discrete 
X_discrete = np.arange(1, 7) 
discrete_uniform = stats.randint(1, 7) 
discrete_uniform_pmf = discrete_uniform.pmf(X_discrete)
 
# plot both tables 
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,5)) 
# discrete plot 
ax[0].bar(X_discrete, discrete_uniform_pmf) 
ax[0].set_xlabel("X") 
ax[0].set_ylabel("Probability") 
ax[0].set_title("Discrete Uniform Distribution") 
# continuous plot 
ax[1].plot(X_continuous, continuous_uniform_pdf) 
ax[1].set_xlabel("X") 
ax[1].set_ylabel("Probability") 
ax[1].set_title("Continuous Uniform Distribution") 
plt.show()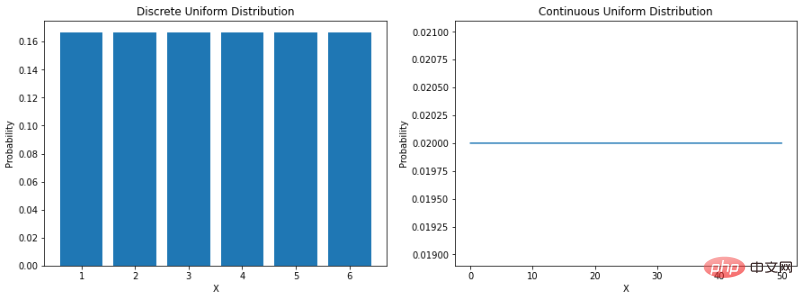

ガウス分布

ガウス分布は、おそらく最もよく聞かれ、馴染みのある分布です。これにはいくつかの名前があります。確率プロットが鐘のように見えるため鐘曲線と呼ぶ人、最初に記述したドイツの数学者カール ガウスが命名したためガウス分布と呼ぶ人、初期の統計学者が気づいたため正規分布であるという人もいます。何度も何度も起こること。正規分布の確率密度関数は次のとおりです。σ は標準偏差、μ は分布の平均です。正規分布では、平均値、最頻値、中央値がすべて等しいことに注意してください。正規分布の確率変数をプロットすると、曲線は平均に関して対称になります。値の半分は中心の左側にあり、半分は中心の右側にあります。そして、曲線の下の総面積は 1 です。

mu = 0 
variance = 1 
sigma = np.sqrt(variance) 
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100) 
 
plt.subplots(figsize=(8, 5)) 
plt.plot(x, stats.norm.pdf(x, mu, sigma)) 
plt.title("Normal Distribution") 
plt.show()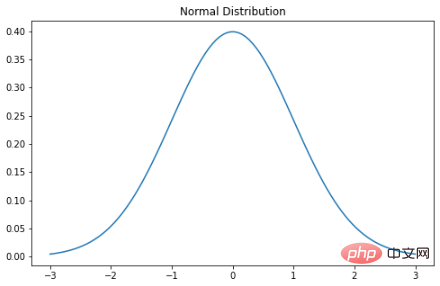

正規分布の場合。経験則により、データの何パーセントが平均から一定の標準偏差の範囲内に収まるかがわかります。これらのパーセンテージは次のとおりです:

• データの 68% が平均の 1 標準偏差以内に収まります。
• データの 95% は、平均値の 2 標準偏差以内に収まります。
• 99.7% のデータは、平均値の 3 標準偏差以内に収まります。

対数正規分布

対数正規分布は、対数正規分布の確率分布を持つ連続確率変数です。したがって、確率変数 X が対数正規分布している場合、Y = ln(X) は正規分布になります。対数正規分布の PDF は次のとおりです。 対数正規分布の確率変数は、正の実数値のみを受け取ります。したがって、対数正規分布は右に歪んだ曲線を作成します。 Python でプロットしてみましょう:

X = np.linspace(0, 6, 500) 
 
std = 1 
mean = 0 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
 
fig, ax = plt.subplots(figsize=(8, 5)) 
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=1") 
ax.set_xticks(np.arange(min(X), max(X))) 
 
std = 0.5 
mean = 0 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=0.5") 
 
std = 1.5 
mean = 1 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
plt.plot(X, lognorm_distribution_pdf, label="μ=1, σ=1.5") 
 
plt.title("Lognormal Distribution") 
plt.legend() 
plt.show()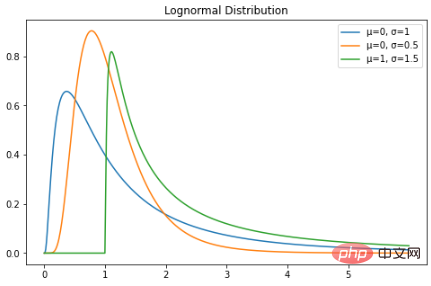

ポアソン分布

ポアソン分布は、フランスの数学者 Simon Denis Poisson にちなんで名付けられました。これは離散確率分布であり、有限の結果を持つイベントをカウントすることを意味します。つまり、カウント分布です。したがって、ポアソン分布は、指定された期間内にイベントが発生する回数を示すために使用されます。イベントが一定の時間率で発生する場合、時間内にイベントの数 (n) を観測する確率はポアソン分布で表すことができます。たとえば、顧客は 1 分あたり平均 3 回の割合でコーヒー ショップに到着するとします。ポアソン分布を使用して、2 分以内に 9 人の顧客が到着する確率を計算できます。確率質量関数の式は次のとおりです。 λ は 1 単位時間内のイベント率です。この場合、それは 3 です。 k は出現回数です。この場合は 9 です。ここで Scipy を使用して確率計算を完了できます。

from scipy import stats 

print(stats.poisson.pmf(k=9, mu=3))

0.002700503931560479

ポアソン分布の曲線は正規分布に似ており、λ はピーク値を表します。

X = stats.poisson.rvs(mu=3, size=500) 
 
plt.subplots(figsize=(8, 5)) 
plt.hist(X, density=True, edgecolor="black") 
plt.title("Poisson Distribution") 
plt.show()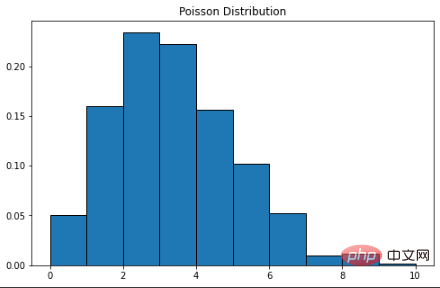

指数分布

指数分布是泊松点过程中事件之间时间的概率分布。指数分布的概率密度函数如下：λ 是速率参数，x 是随机变量。

X = np.linspace(0, 5, 5000) 
 
exponetial_distribtuion = stats.expon.pdf(X, loc=0, scale=1) 
 
plt.subplots(figsize=(8,5)) 
plt.plot(X, exponetial_distribtuion) 
plt.title("Exponential Distribution") 
plt.show()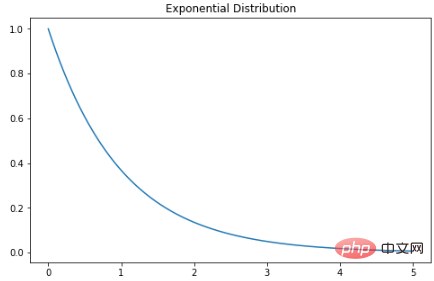

二项分布

可以将二项分布视为实验中成功或失败的概率。有些人也可能将其描述为抛硬币概率。参数为 n 和 p 的二项式分布是在 n 个独立实验序列中成功次数的离散概率分布，每个实验都问一个是 - 否问题，每个实验都有自己的布尔值结果：成功或失败。本质上，二项分布测量两个事件的概率。一个事件发生的概率为 p，另一事件发生的概率为 1-p。这是二项分布的公式：

• P = 二项分布概率
• = 组合数
• x = n次试验中特定结果的次数
• p = 单次实验中，成功的概率
• q = 单次实验中，失败的概率
• n = 实验的次数

可视化代码如下：

X = np.random.binomial(n=1, p=0.5, size=1000) 
 
plt.subplots(figsize=(8, 5)) 
plt.hist(X) 
plt.title("Binomial Distribution") 
plt.show()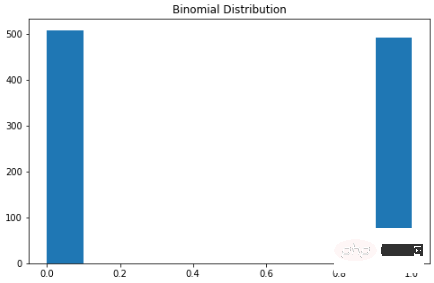

学生 t 分布

学生 t 分布（或简称 t 分布）是在样本量较小且总体标准差未知的情况下估计正态分布总体的均值时出现的连续概率分布族的任何成员。它是由英国统计学家威廉·西利·戈塞特（William Sealy Gosset）以笔名“student”开发的。PDF如下：n 是称为“自由度”的参数，有时可以看到它被称为“d.o.f.” 对于较高的 n 值，t 分布更接近正态分布。

import seaborn as sns 
from scipy import stats 
 
X1 = stats.t.rvs(df=1, size=4) 
X2 = stats.t.rvs(df=3, size=4) 
X3 = stats.t.rvs(df=9, size=4) 
 
plt.subplots(figsize=(8,5)) 
sns.kdeplot(X1, label = "1 d.o.f") 
sns.kdeplot(X2, label = "3 d.o.f") 
sns.kdeplot(X3, label = "6 d.o.f") 
plt.title("Student's t distribution") 
plt.legend() 
plt.show()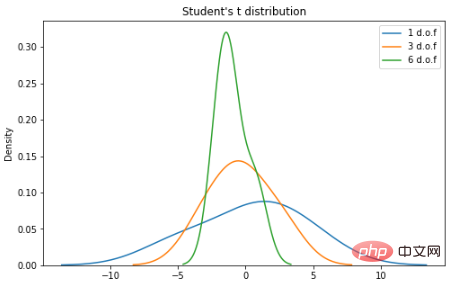

卡方分布

卡方分布是伽马分布的一个特例；对于 k 个自由度，卡方分布是一些独立的标准正态随机变量的 k 的平方和。PDF如下：这是一种流行的概率分布，常用于假设检验和置信区间的构建。在 Python 中绘制一些示例图：

X = np.arange(0, 6, 0.25) 
 
plt.subplots(figsize=(8, 5)) 
plt.plot(X, stats.chi2.pdf(X, df=1), label="1 d.o.f") 
plt.plot(X, stats.chi2.pdf(X, df=2), label="2 d.o.f") 
plt.plot(X, stats.chi2.pdf(X, df=3), label="3 d.o.f") 
plt.title("Chi-squared Distribution") 
plt.legend() 
plt.show()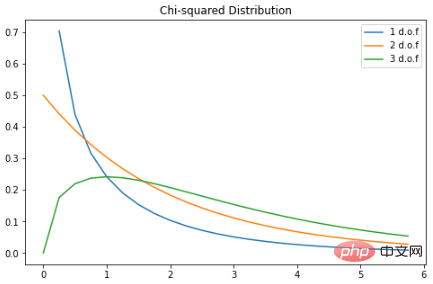

掌握统计学和概率对于数据科学至关重要。在本文展示了一些常见且常用的分布，希望对你有所帮助。

以上がPython は 8 つの確率分布公式とデータ視覚化チュートリアルを実装しますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。