ホームページ >テクノロジー周辺機器 >AI >香港らによって提案された因果表現学習方法は、複雑な正書法データ分布の外部一般化問題を目的としています。
香港らによって提案された因果表現学習方法は、複雑な正書法データ分布の外部一般化問題を目的としています。
- 王林転載
- 2023-04-25 22:22:071448ブラウズ
ディープ ラーニング モデルの適用と推進により、モデルはより高いトレーニング パフォーマンスを得るためにデータ内の偽相関 (Spurious Correlation) を使用することが多いことが徐々に分かってきました。ただし、そのような相関関係はテスト データには当てはまらないことが多いため、そのようなモデルのテスト パフォーマンスは満足のいくものではないことがよくあります [1]。本質的には、従来の機械学習の目標 (経験的リスク最小化、ERM) は、トレーニング セットとテスト セットの独立した同一の分布特性を前提としていますが、実際には、独立した同一の分布の仮定が当てはまるシナリオは多くの場合、限られているということです。現実の多くのシナリオでは、トレーニング データの分布とテスト データの分布には通常、不一致、つまり分布シフト (分布シフト) が見られます。このようなシナリオでモデルのパフォーマンスを向上させることを目的とした問題は、通常、次のように呼ばれます。 of-distribution 一般化 (out-of-distribution 一般化)、Out-of-Distribution) 問題。 ERM など、データの因果関係ではなく相関関係の学習に焦点を当てたクラスの手法は、分布の変化に苦戦することがよくあります。近年多くの手法が登場し、因果推論の不変性原理を利用して分布外の問題に一定の進歩を遂げていますが、グラフデータに関する研究はまだ限られています。これは、グラフ データの分布外一般化が従来のヨーロッパのデータよりも難しく、グラフ機械学習にさらなる課題をもたらすためです。この論文では、グラフ分類タスクを例として取り上げ、因果不変性の原則に基づいたグラフ分布の超一般化を検討します。
# 近年、因果不変性の原理の助けを借りて、人々は分布外の問題で一定の成功を収めてきました。ユークリッド データの一般化 (ただしグラフの場合) データに関する研究は依然として限られています。ユークリッド データとは異なり、グラフの複雑さにより、因果不変性の原則を使用し、分布外の汎化の困難を克服する際に特有の課題が生じます。
この課題に対処するために、この研究では因果不変性をグラフ機械学習に統合し、グラフ データの問題を解決するための因果関係にヒントを得た不変グラフ学習フレームワークを提案します。分布外の一般化は、新しい理論と方法を提供します。
この論文は、NeurIPS 2022 に掲載されました。この研究は、香港中文大学、香港バプテスト大学、テンセント AI ラボ、シドニー大学の協力により完成しました。

- 論文タイトル: グラフ上の分布外一般化のための因果不変表現の学習
- ##論文リンク: https://openreview.net/forum?id=A6AFK_JwrIW
- プロジェクト コード: https:// github.com/LFhase/CIGA グラフ データの分布外の一般化
分布外のグラフ データの一般化グラフデータの難しさは何ですか?
近年、グラフ ニューラル ネットワークは、レコメンデーション システム、AI 支援医薬品、その他の分野など、グラフ構造を伴う機械学習アプリケーションで大きな成功を収めています。ただし、既存のグラフ機械学習アルゴリズムのほとんどはデータの独立した同一の分布の仮定に依存しているため、テスト データとトレーニング データにシフト (分布シフト) があると、アルゴリズムのパフォーマンスが大幅に低下します。同時に、グラフ データ構造の複雑さにより、分布外のグラフ データの一般化はヨーロッパのデータよりも一般的であり、より困難です。
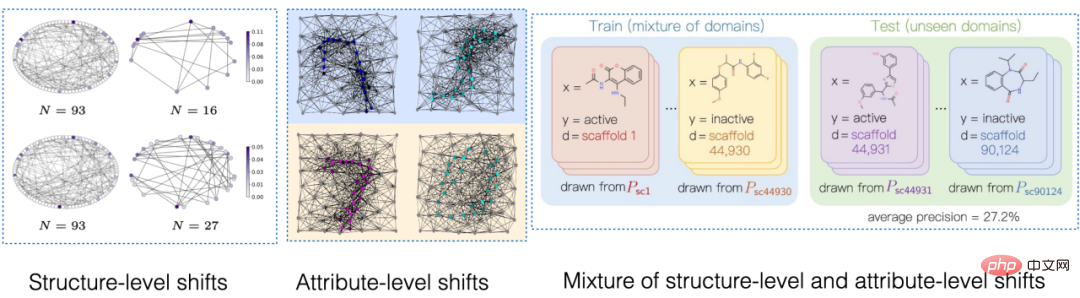
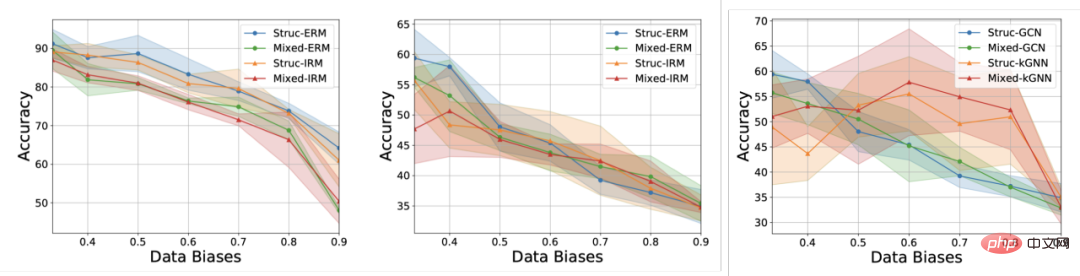
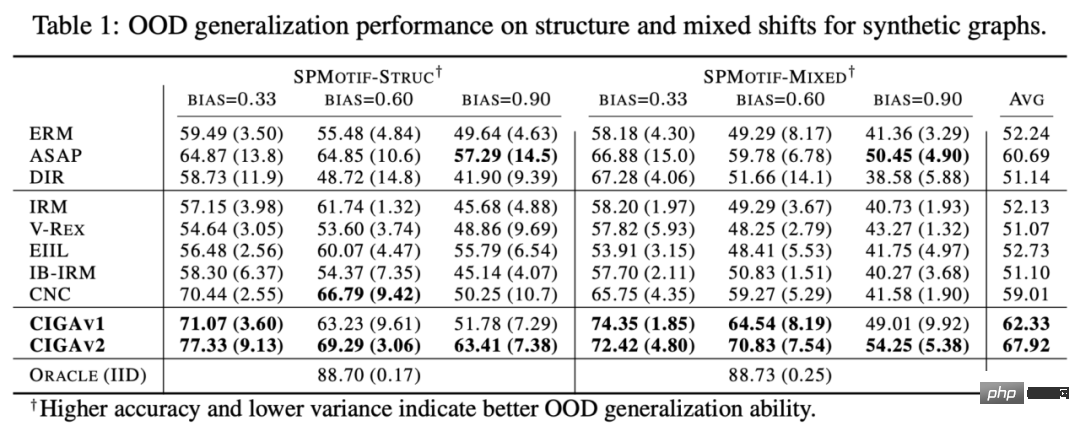
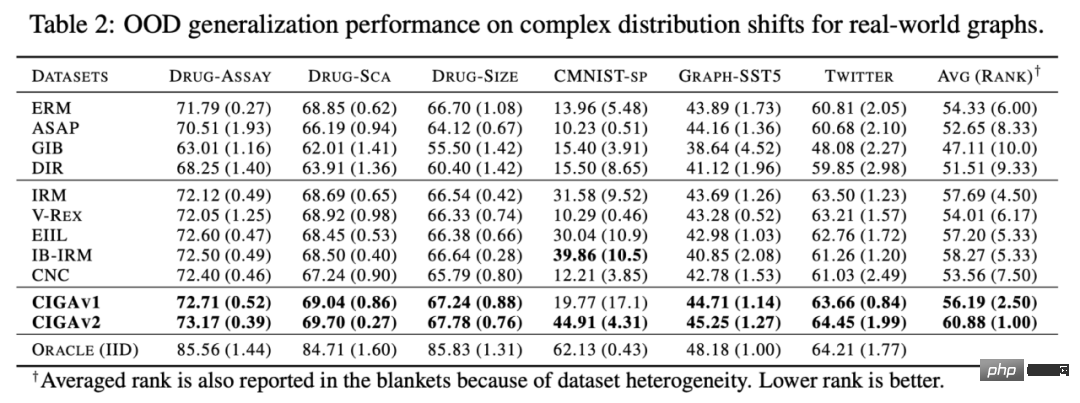
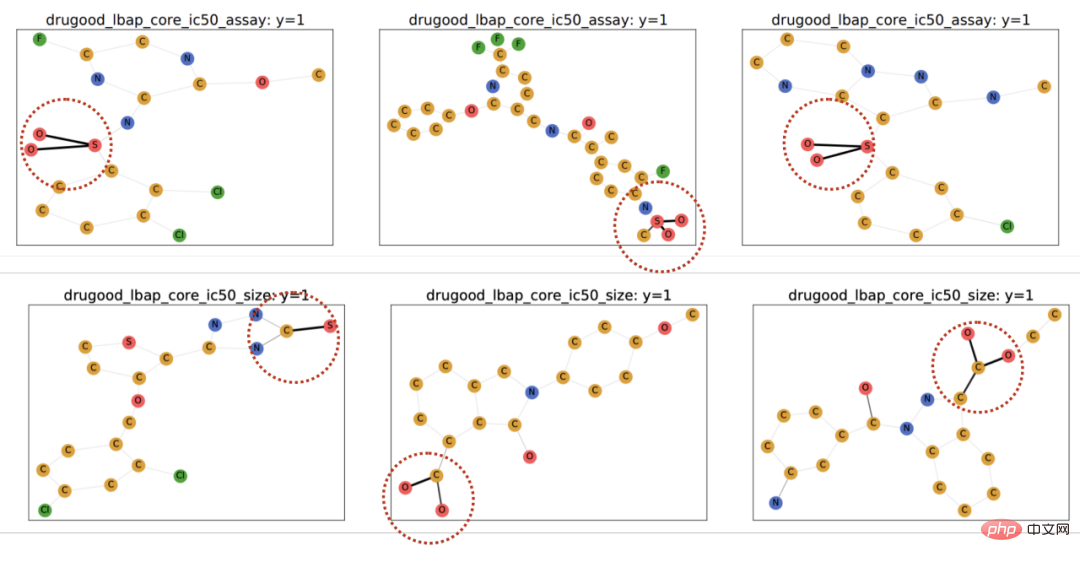
# 図 1. グラフ上の分布シフトの例。 まず第一に、グラフ データの分布シフトは、グラフのノード特徴量分布に現れる可能性があります (属性レベルのシフト)。たとえば、レコメンデーション システムでは、トレーニング データに含まれる製品がいくつかの人気のあるカテゴリに属している可能性があり、関与するユーザーも特定の地域に属している可能性がありますが、テスト段階では、システムはすべての地域のユーザーを適切に処理する必要があります。カテゴリーと地域、商品[2,3,4]。さらに、グラフ データの分布のシフトは、グラフの構造分布にも現れることがあります (構造レベルのシフト)。 2019 年にはすでに、より小さなグラフでトレーニングされたグラフ ニューラル ネットワークは、より大きなグラフに一般化するための効果的な注意 (アテンション) の重みを学習するのが難しいことに人々が気づきました [5]。これにより、一連の関連研究も提案されました [6,7]。現実のシナリオでは、これら 2 種類の分布シフトが同時に現れることが多く、異なるレベルでのこれらの分布シフトには、予測対象のラベルとの異なる誤った相関パターンがある可能性もあります。たとえば、レコメンデーション システムでは、特定のカテゴリの製品と特定の地域のユーザーが製品ユーザー インタラクション グラフ上で固有のトポロジー構造を示すことがよくあります [4]。薬物分子の属性の予測では、トレーニングに関与する薬物分子が小さすぎる可能性があり、予測結果は実験の測定環境にも影響を受けます [8]。 さらに、ユークリッド空間における分布外一般化では、データが複数の環境 (Environment) またはドメイン (Domain) から取得されると仮定し、さらにモデルが取得できると仮定します。トレーニング中のトレーニング データ 各サンプルが属する環境は、環境間の不変性を調査します。ただし、データの環境ラベルを取得するには、データに関連する専門知識が必要になることが多く、グラフ データの抽象的な性質により、グラフ データの環境ラベルの取得はより高価になります。したがって、OGB などの既存のグラフ データセットのほとんどには、そのような環境ラベル情報が含まれておらず、DrugOOD データセットなどの少数のデータセットに環境ラベルが含まれている場合でも、さまざまな程度のノイズが存在します。 既存の手法は、グラフ上の分布外一般化の問題を解決できますか? グラフ データの分布外一般化の課題を直感的に理解するために、Spurious-Motif [9] データセットに基づいて新しいデータを構築し、さらに分析を進めます。上記のいくつかの主要な課題をインスタンス化し、ヨーロッパのデータの分布外一般化のためのトレーニング ターゲット IRM [10] や、より強力な表現力を備えた GNN [11] などの既存の手法を使用して、グラフ データを分析できるかどうかを分析します。既存の方法で解決される 配布外の一般化の問題。 図 2. スプリアス モチーフ データセットの例。 Spurious Motif タスクを図 2 に示します。このタスクは主に、入力グラフに特定の構造 (House など) を持つサブグラフが含まれているかどうかに基づいてグラフにラベルを付けます。ノードの属性をノードの色で表すかどうかを判断します。このデータ セットを使用すると、グラフ ニューラル ネットワークのパフォーマンスに対するさまざまなレベルでの分布シフトの影響を明確にテストできます。 ERM を使用してトレーニングされた通常の GNN モデルの場合: さらに、モデルはトレーニング中に環境ラベルに関連する情報を取得できません。実験結果を図 3 に示します (詳細な結果は付録 D にあります)。紙の)。 # 図 3. さまざまなグラフ分布シフトにおける既存のメソッドのパフォーマンス。 図 3 に示すように、通常の GCN は、ERM を使用してトレーニングされたか IRM を使用してトレーニングされたかにかかわらず、グラフの構造変化 (Struc) に対処できません。グラフ ノード属性オフセット (混合) とグラフ サイズ分布オフセット (図 3) を追加すると、モデルのパフォーマンスはさらに低下し、さらに、より強力な表現力を持つ kGNN を使用した場合でも、深刻なパフォーマンスの低下を避けることは困難です (平均パフォーマンスが低い、または分散が大きい)。 ここから、当然のことながら、研究すべき質問につながります。さまざまなグラフ分布のシフトに対処できる GNN モデルを取得するにはどうすればよいでしょうか? 上記の問題を解決するには、ターゲット、つまり不変グラフ ニューラル ネットワーク (インバリアント GNN)、最悪の環境でも良好にパフォーマンスするモデルとして定義します (厳密な定義については論文を参照してください): 定義 1 (インバリアント グラフ ニューラル ネットワーク) 与えられた系列収集されたグラフ分類データセット さまざまな因果関係のある環境 、ここで 含まれるものe は、環境からの独立した同一に分散されたサンプルであると考えられます。e グラフ ニューラル ネットワーク を考えます。ここで、 と はそれぞれ入力として使用されるグラフ空間とサンプル空間です。 f は、 の場合に限り、つまり、すべての環境の最大値 最悪の経験的リスク。 は環境内のモデルの経験損失です。 モデルはトレーニング中にトレーニング環境 のデータの一部しか取得できません。データ プロセスについて仮定が行われていない場合、グラフ ニューラル ネットワークの定義で必要とされる minmax 最適性を達成することは困難です。したがって、構造因果モデルを使用して因果推論の観点からグラフ生成プロセスをモデル化し、グラフ データの因果不変性を定義するために環境間の相関関係を特徴付けます。 # 図 4. グラフ データ生成プロセスの因果モデル。 #。さらに、潜在変数 さらに、C は潜在空間内で Y、S、E と多くの種類の相互作用を持っています。主に、偽の潜在変数 S とラベル Y が定数の潜在変数 C 以外に追加の関連性を持っているかどうかに従います。 #上記の因果分析に基づいて、モデルが予測に不変サブグラフのみを使用する場合、つまり、## 間のサブグラフのみを使用することがわかります。 # 相関関係、モデルの予測は環境 E の変化の影響を受けません; 逆に、モデルの予測が S または このうち、 を検討します。このような状況では、 内の誤ったサブグラフの可能性を「絞り出す」ために、因果モデル # から # に関するさらなる情報をさらに求めます。 #ユニークな属性。 PIIF または FIIF の誤った相関タイプに関係なく、ラベル Y の相互情報量を最大化するサブグラフについては、次のようになります。 # と推測できます。 同時に と と を最大化すると、 CIGA の実装: 実際には、2 つのサブグラフの相互情報量を推定することは難しいことがよくありますが、教師あり対照学習 [11] が可能な解決策を提供します。 : # 実験では、16 の合成データセットまたは実世界のデータセットを使用して、さまざまなグラフ分布シフトの下で CIGA を実行しました。実験では、解釈可能な GNN フレームワーク [9] を使用して CIGA のプロトタイプを実装しましたが、実際には CIGA にはさらに多くの実装方法があります。特定のデータセットと実験の詳細については、記事の実験セクションを参照してください。 合成データセットにおける構造分布シフトと混合分布シフトのパフォーマンス 最初は SPMotif データセットに基づいていました[9] は、SPMotif-Struc および SPMotif-Mixed データ セットを構築しました。ここで、SPMotif-Struc には、グラフ内の特定のサブグラフと他のサブグラフ構造間の偽の相関、およびグラフ サイズの分布シフトが含まれていますが、SPMotif-Mixed Based on SPMotif-Struc 、グラフ ノード属性レベルで新しい分布オフセットが追加されます。表の最初の列は ERM と解釈可能な GNN のベースラインで、2 番目の列はユークリッド空間における最も高度な分布外一般化アルゴリズムです。結果から、より優れた GNN フレームワークとユークリッド空間の分布外汎化アルゴリズムの両方がグラフ上の分布シフトの影響を受け、より多くの分布シフトが発生すると、パフォーマンスの損失 (平均分類パフォーマンスが小さくなる) が発生することがわかります。またはより大きな分散)はさらに強化されます。対照的に、CIGA は、さまざまな強度の分布シフトの下でも良好なパフォーマンスを維持し、最高のベースライン パフォーマンスを大幅に上回ります。 #実際のデータセットにおけるさまざまなグラフ分布シフトのパフォーマンス # #We次に、AI支援医薬品における薬物分子属性予測からのDrugOOD(実験環境アッセイ、分子)の3つの異なる環境部門を含む、実際のデータセットおよびさまざまな実際のデータに存在するグラフ分布シフトに対するCIGAのパフォーマンスをさらにテストしました。 (足場、分子サイズ) には、さまざまな実際のアプリケーション シナリオのグラフ分布シフトが含まれています。ユークリッド空間の古典的な画像データ セット ColoredMNIST [10] に基づいて変換された CMNIST-SP には、主にグラフ ノードが含まれています。属性の PIIF タイプの分布オフセットに基づいています。 Graph-SST5 と Twitter [15] は自然言語感情分類データセット SST5 と Twitter から変換され、グラフ次数の追加の分布オフセットが追加されます。さらに、以前に研究された 4 つの分子グラフ サイズ分布シフト データ セット [7]、 も使用しました。 #テスト結果は上の表に示されていますが、実際のデータでは、タスクの難易度が上昇したため、 、より優れたアーキテクチャを備えた GNN が使用されるか、ユークリッド空間で分布外汎化最適化ターゲットをトレーニングすることによって得られるモデルのパフォーマンスは、ERM を使用してトレーニングされた通常の GNN モデルよりもさらに低くなります。この現象は、ユークリッド空間でのより困難なタスクの下での分布外一般化実験で観察される現象 [16] にも似ており、実データに対する分布外一般化の難しさと既存の方法の欠点を反映しています。対照的に、CIGA はすべての実データとグラフ分布の変化を改善し、Twitter や PROTEINS などの一部のデータセットでは経験的に最適な Oracle レベルに到達することさえできます。グラフ分類データ セットに関する上記の最新のグラフ分布外一般化テスト ベンチマーク GOOD に関する予備テストでは、CIGA が現在、さまざまなグラフ分布のシフトに対処できる最良のグラフ分布外一般化アルゴリズムであることも示しています。 Interpretable GNN が CIGA のプロトタイプ実装アーキテクチャとして使用されているため、モデルによって特定された DrugOOD も視覚化し、CIGA がいくつかの比較的一貫した分子塩基を見つけたことがわかりました。分子の物性予測。これにより、その後の AI 支援医薬品のより良い基盤が提供される可能性があります。 図 6. DrugOOD の CIGA によって認識された部分的に不変のサブグラフ。 この論文では、因果推論の観点から、さまざまなグラフ分布のシフトの下でのグラフ分布への因果不変性を初めて導入します。外部一般化問題では、新しい理論的に保証された解のフレームワーク CIGA が提案されています。多数の実験によって、CIGA の優れた配布外汎化パフォーマンスも完全に検証されています。将来に目を向けると、CIGA に基づいて、より優れた実装フレームワーク [17] をさらに探索したり、理論的に保証された CIGA 用のより優れたデータ拡張方法を導入したり [3,18]、グラフ上の関連性を理論的にモデル化することができます。 ) [19] 不変サブグラフを識別する CIGA の能力をさらに強化し、AI 支援医薬品などの実際のアプリケーション シナリオにおけるグラフ ニューラル ネットワークの実際の実装を促進します。 
グラフ データ分布外の一般化の因果モデル
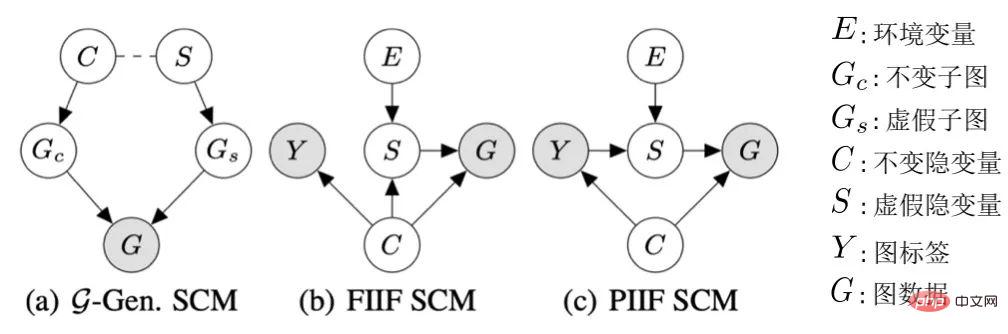
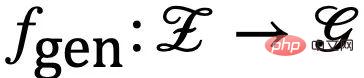 について、環境 E の影響を受けるかどうかに応じて、不変の潜在変数
について、環境 E の影響を受けるかどうかに応じて、不変の潜在変数  と偽の潜在変数に分割します。 (偽の潜在変数)
と偽の潜在変数に分割します。 (偽の潜在変数)  。同様に、潜在変数 C と S はそれぞれ、G の特定のサブグラフの生成に影響を与えます。これらは、それぞれ不変サブグラフ
。同様に、潜在変数 C と S はそれぞれ、G の特定のサブグラフの生成に影響を与えます。これらは、それぞれ不変サブグラフ 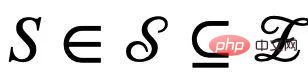 と偽サブグラフ
と偽サブグラフ  として記録されます。 、図 4 (a) に示すように、C は主にグラフのラベル Y を制御します。これはさらに派生することもできます
として記録されます。 、図 4 (a) に示すように、C は主にグラフのラベル Y を制御します。これはさらに派生することもできます  つまり、C と Y は S よりも高い相互情報量を持っています。この生成プロセスは多くの実践例に対応しており、例えば、分子の薬効は通常、特定の主要なグループ (分子サブグラフ) (分子に対するヒドロキシル-H2O の水溶解度など) によって決まります。
つまり、C と Y は S よりも高い相互情報量を持っています。この生成プロセスは多くの実践例に対応しており、例えば、分子の薬効は通常、特定の主要なグループ (分子サブグラフ) (分子に対するヒドロキシル-H2O の水溶解度など) によって決まります。 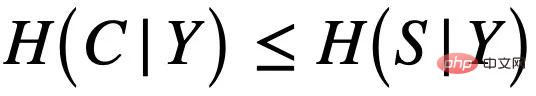
 は、図 4 (b) に示す FIIF (完全情報不変特徴) と、図 4(c) に示す PIIF (部分情報不変特徴) の 2 つのタイプに要約できます。このうち FIIF は、不変情報が与えられたラベルが誤った相関量に依存しないことを意味します。 PIIFはその逆です。可能な限り多くのグラフ分布の変化をカバーするために、私たちの因果モデルはさまざまなグラフ生成モデルを広範にモデル化するよう努めていることに注意してください。グラフ生成プロセスについてさらに知識があれば、図 4 に示す因果モデルをより具体的な例にさらに一般化できます。付録 C.1 と同様に、追加のグラフ制限 (グラフン) の仮定を追加することで、グラフ サイズ分布のシフトの分析に関する Bevilacqua らによる以前の研究 [7] に因果グラフを一般化する方法を示します。
は、図 4 (b) に示す FIIF (完全情報不変特徴) と、図 4(c) に示す PIIF (部分情報不変特徴) の 2 つのタイプに要約できます。このうち FIIF は、不変情報が与えられたラベルが誤った相関量に依存しないことを意味します。 PIIFはその逆です。可能な限り多くのグラフ分布の変化をカバーするために、私たちの因果モデルはさまざまなグラフ生成モデルを広範にモデル化するよう努めていることに注意してください。グラフ生成プロセスについてさらに知識があれば、図 4 に示す因果モデルをより具体的な例にさらに一般化できます。付録 C.1 と同様に、追加のグラフ制限 (グラフン) の仮定を追加することで、グラフ サイズ分布のシフトの分析に関する Bevilacqua らによる以前の研究 [7] に因果グラフを一般化する方法を示します。 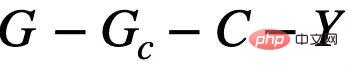 に関連する情報に依存している場合、その予測結果は次の影響を受けます。 E の変化 重大な変化が発生し、パフォーマンスが低下します。したがって、私たちの目標は、不変グラフ ニューラル ネットワークの学習から、a) 潜在的な不変サブグラフの特定、b) 特定されたサブグラフを使用した Y の予測までさらに洗練することができます。データ生成のアルゴリズムプロセスにさらに対応するために、グラフ ニューラル ネットワークをさらにサブグラフ認識ネットワーク (Featurizer GNN)
に関連する情報に依存している場合、その予測結果は次の影響を受けます。 E の変化 重大な変化が発生し、パフォーマンスが低下します。したがって、私たちの目標は、不変グラフ ニューラル ネットワークの学習から、a) 潜在的な不変サブグラフの特定、b) 特定されたサブグラフを使用した Y の予測までさらに洗練することができます。データ生成のアルゴリズムプロセスにさらに対応するために、グラフ ニューラル ネットワークをさらにサブグラフ認識ネットワーク (Featurizer GNN)  と分類ネットワーク (Classifier GNN)
と分類ネットワーク (Classifier GNN)  # に分割します。 ## および
# に分割します。 ## および 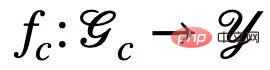 (
(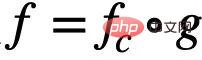 は
は  のサブグラフ空間です)。この場合、モデルの学習目標は式 (1) のように表すことができます。
のサブグラフ空間です)。この場合、モデルの学習目標は式 (1) のように表すことができます。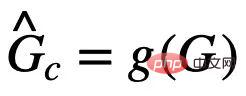 は部分グラフ認識ネットワークによる不変部分グラフの予測です。
は部分グラフ認識ネットワークによる不変部分グラフの予測です。 は
は  です。 Y との相互情報量、つまり
です。 Y との相互情報量、つまり 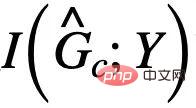 の最大化は、Y を予測するために
の最大化は、Y を予測するために  を使用する経験的損失を最小限に抑えることで達成できます。ただし、E が欠落しているため、E を直接使用して
を使用する経験的損失を最小限に抑えることで達成できます。ただし、E が欠落しているため、E を直接使用して  の独立性を検証することは困難です。そのためには、必要性を特定するために他の同等の条件を探す必要があります。の 。
の独立性を検証することは困難です。そのためには、必要性を特定するために他の同等の条件を探す必要があります。の 。 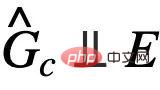 原因にヒントを得た不変グラフ学習
原因にヒントを得た不変グラフ学習 欠落時の不変部分グラフの識別の問題を解決するために、式 (1) の枠組みに基づいて、次のようにしたいと考えています。式 (1) の簡単に実装可能な等価条件を求めます。特に、最初に、基礎となる不変サブグラフ サイズが固定され既知である、より単純なケース
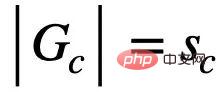 を最大化することを検討してください。
を最大化することを検討してください。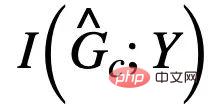 は
は  と同じサイズですが、
と同じサイズですが、 # であるためです。 ## は Y にも関連しているため、他の制約を付けずに
# であるためです。 ## は Y にも関連しているため、他の制約を付けずに  を最大化すると、推定された不変サブグラフに Y の偽サブグラフと相互情報を持つ部分が含まれる可能性があります。
を最大化すると、推定された不変サブグラフに Y の偽サブグラフと相互情報を持つ部分が含まれる可能性があります。 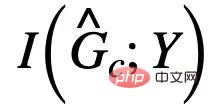
上記 2 つのプロパティを組み合わせると、 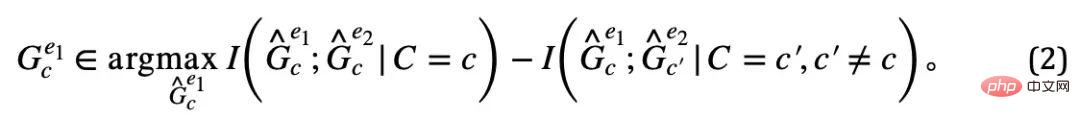 ## 実際に直接観察することは難しいため、式 (2) で代用することができます。
## 実際に直接観察することは難しいため、式 (2) で代用することができます。 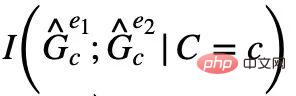 が同時に最大値に達した場合、
が同時に最大値に達した場合、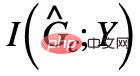 は自動的に最小化されます。そうでない場合、モデルの予測は単純な解決策に崩壊します。これから、単純なケースにおける不変部分グラフの同値条件を取得しました。式 (1) と組み合わせることで、因果関係にインスピレーションを得た不変グラフ学習 (Causality-inspired Invariant Graph leArning) フレームワークの最初のバージョンが得られました。つまり、CIGAv1:
は自動的に最小化されます。そうでない場合、モデルの予測は単純な解決策に崩壊します。これから、単純なケースにおける不変部分グラフの同値条件を取得しました。式 (1) と組み合わせることで、因果関係にインスピレーションを得た不変グラフ学習 (Causality-inspired Invariant Graph leArning) フレームワークの最初のバージョンが得られました。つまり、CIGAv1: 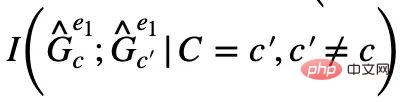
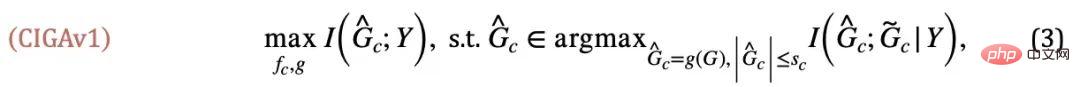 ここで、
ここで、 、つまり
、つまり  と G は同じカテゴリ Y に属します。私たちの論文では、グラフ サイズが既知の場合、CIGAv1 が図 4 に対応する因果モデル内の潜在的な不変サブグラフを首尾よく識別できることをさらに実証します。ただし、これまでの仮定が理想的すぎるため、実際には不変部分グラフのサイズが変化する可能性があり、対応するサイズが不明なことがよくあります。サブグラフ サイズがないという仮定の下では、グラフ全体を不変サブグラフとして識別するだけで CIGAv1 要件を満たすことができます。したがって、この仮定を取り除くために、不変部分グラフに関する特性をさらに求めることを検討します。
と G は同じカテゴリ Y に属します。私たちの論文では、グラフ サイズが既知の場合、CIGAv1 が図 4 に対応する因果モデル内の潜在的な不変サブグラフを首尾よく識別できることをさらに実証します。ただし、これまでの仮定が理想的すぎるため、実際には不変部分グラフのサイズが変化する可能性があり、対応するサイズが不明なことがよくあります。サブグラフ サイズがないという仮定の下では、グラフ全体を不変サブグラフとして識別するだけで CIGAv1 要件を満たすことができます。したがって、この仮定を取り除くために、不変部分グラフに関する特性をさらに求めることを検討します。 
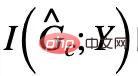 が表示される場合があることに注意してください。
が表示される場合があることに注意してください。  偽のサブグラフ部分## では、削除された不変サブグラフ部分と同じ関連する相互情報を共有します。では、その逆を行って
偽のサブグラフ部分## では、削除された不変サブグラフ部分と同じ関連する相互情報を共有します。では、その逆を行って 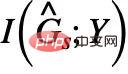 を最大化し、
を最大化し、 # の誤ったサブグラフ部分を削除することはできるでしょうか?答えは「はい」です。
# の誤ったサブグラフ部分を削除することはできるでしょうか?答えは「はい」です。 と Y の相関関係を使用して、
と Y の相関関係を使用して、 # の推定値と競合させることができます。
# の推定値と競合させることができます。 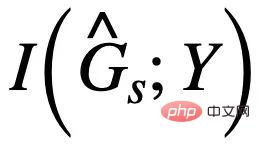 を最大化するときは、
を最大化するときは、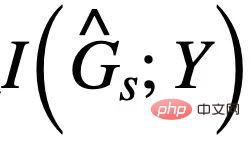 # が
# が 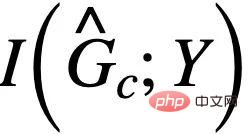 を超えないようにする必要があることに注意してください。そうでない場合は、 will 予測された は再び通常の解に該当します。この追加条件と組み合わせると、式 (3) からサブグラフ サイズが一定であるという仮定を削除し、次の CIGAv2 を取得できます。
を超えないようにする必要があることに注意してください。そうでない場合は、 will 予測された は再び通常の解に該当します。この追加条件と組み合わせると、式 (3) からサブグラフ サイズが一定であるという仮定を削除し、次の CIGAv2 を取得できます。 
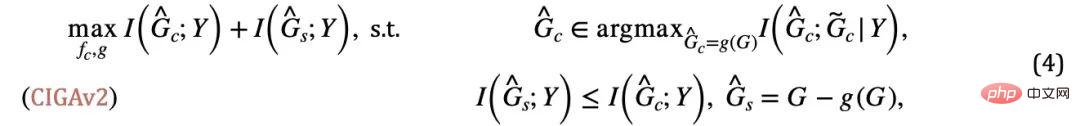
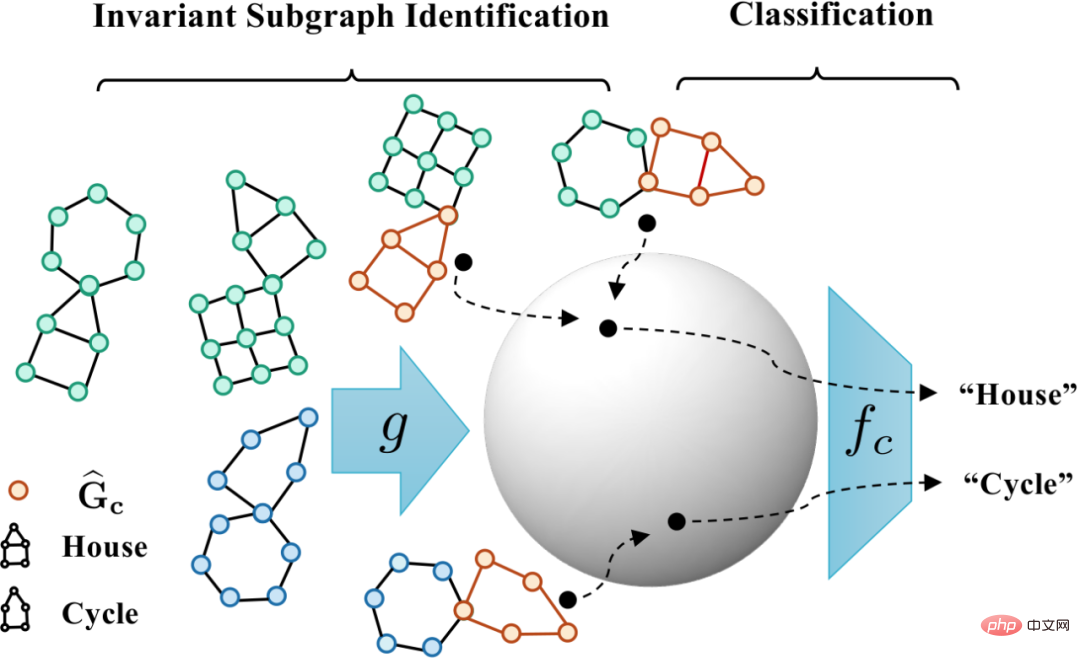 図 5. 因果関係に基づいた不変グラフ学習フレームワークの概略図。
図 5. 因果関係に基づいた不変グラフ学習フレームワークの概略図。  は式 (4) の陽性サンプルに対応し、
は式 (4) の陽性サンプルに対応し、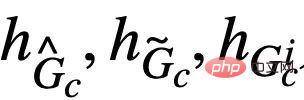 は
は 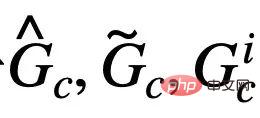 に対応します。 。
に対応します。 。  の場合、式 (5) は、
の場合、式 (5) は、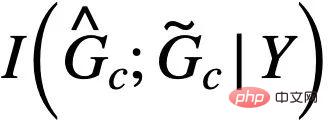 )[13,14] のフォン ミゼス-フィッシャー カーネル密度に基づくノンパラメトリック再置換エントロピー推定量を提供します。 CIGA のコア部分の最終実装を図 5 に示します。つまり、不変サブグラフの同じカテゴリのグラフ表現を潜在表現空間に近づけ、同時に異なるカテゴリのグラフ表現を最大化します。
)[13,14] のフォン ミゼス-フィッシャー カーネル密度に基づくノンパラメトリック再置換エントロピー推定量を提供します。 CIGA のコア部分の最終実装を図 5 に示します。つまり、不変サブグラフの同じカテゴリのグラフ表現を潜在表現空間に近づけ、同時に異なるカテゴリのグラフ表現を最大化します。 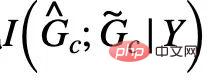 を最大化する不変サブグラフ。さらに、式 (4) の別の制約については、ヒンジ損失、つまり
を最大化する不変サブグラフ。さらに、式 (4) の別の制約については、ヒンジ損失、つまり 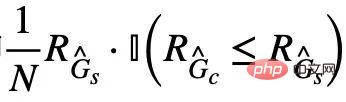 のアイデアを通じて実装できます。予測を最適化する場合にのみ、経験的損失がより大きくなります。対応する不変式 部分グラフの偽の部分グラフ。
のアイデアを通じて実装できます。予測を最適化する場合にのみ、経験的損失がより大きくなります。対応する不変式 部分グラフの偽の部分グラフ。 実験と考察

以上が香港らによって提案された因果表現学習方法は、複雑な正書法データ分布の外部一般化問題を目的としています。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

