Java二分探索ツリーの追加・挿入・削除・作成例を詳しく解説

①概念

二分探索ツリーは二分ソート ツリーとも呼ばれ、空のツリー**、または次のプロパティを持ちます。バイナリ ツリー:

左側のサブツリーが空でない場合、左側のサブツリー上のすべてのノードの値はルート ノードの値より小さくなります。

右側のサブツリーが空でない場合、その値は右側のサブツリー上のすべてのノードの値がルート ノードの値より大きい

その左右のサブツリーも二分探索木です

②操作- 検索

二分探索ツリー検索は二分探索と似ています

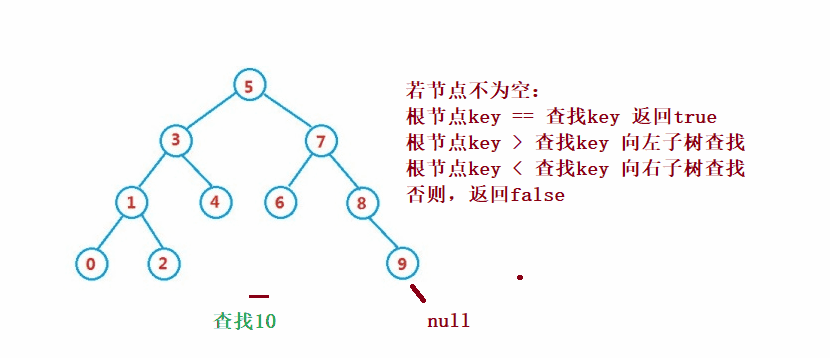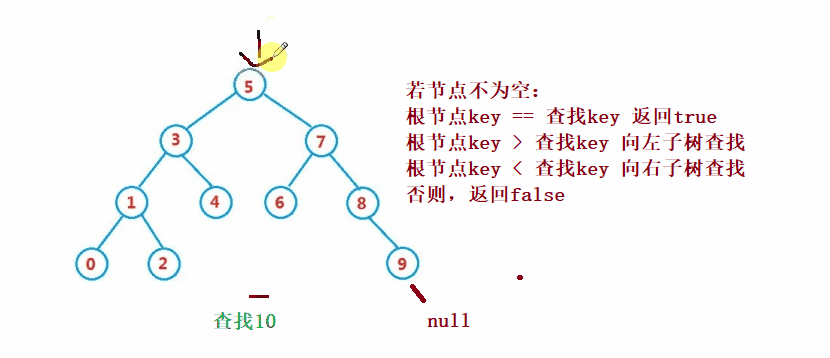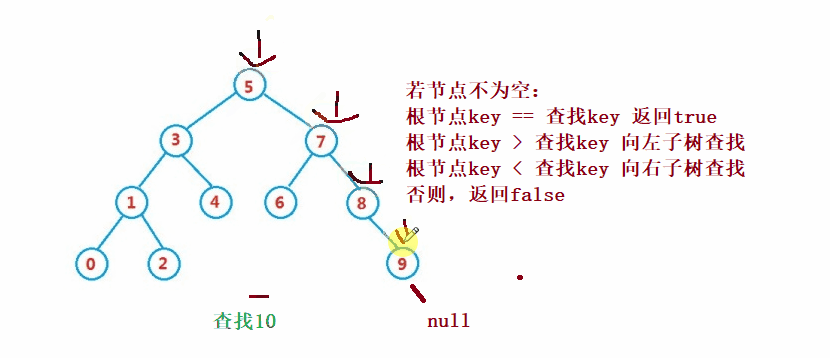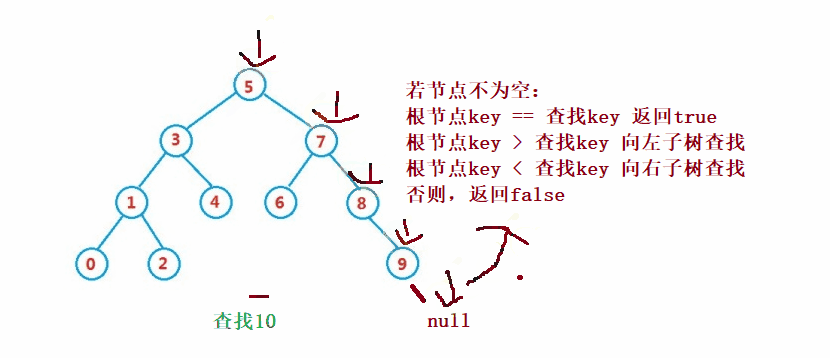
public Node search(int key) {
        Node cur = root;
        while (cur != null) {
            if(cur.val == key) {
                return cur;
            }else if(cur.val < key) {
                cur = cur.right;
            }else {
                cur = cur.left;
            }
        }
        return null;
    }

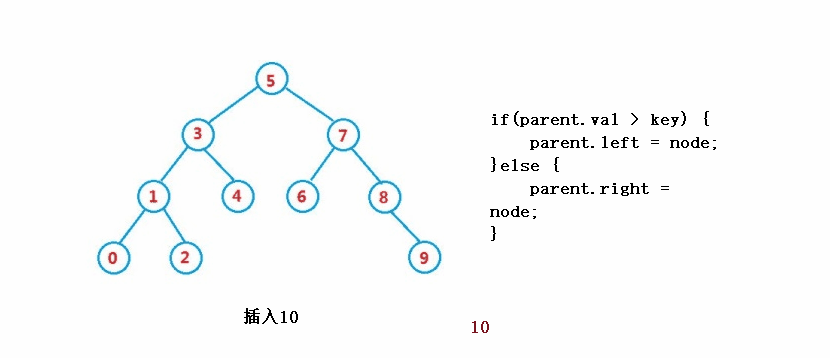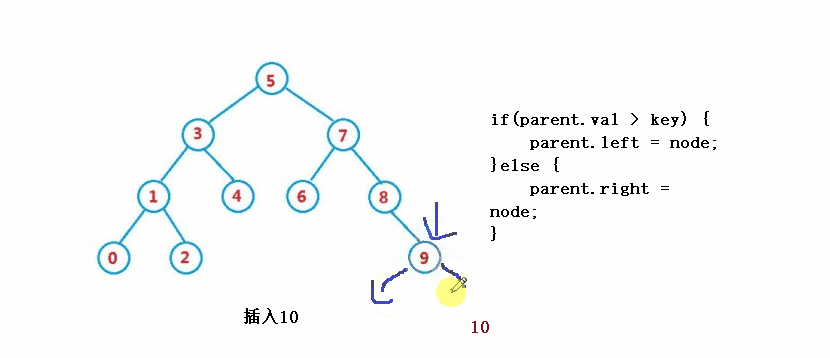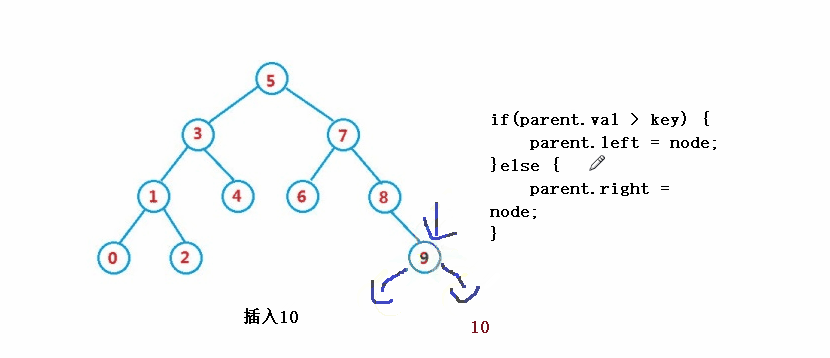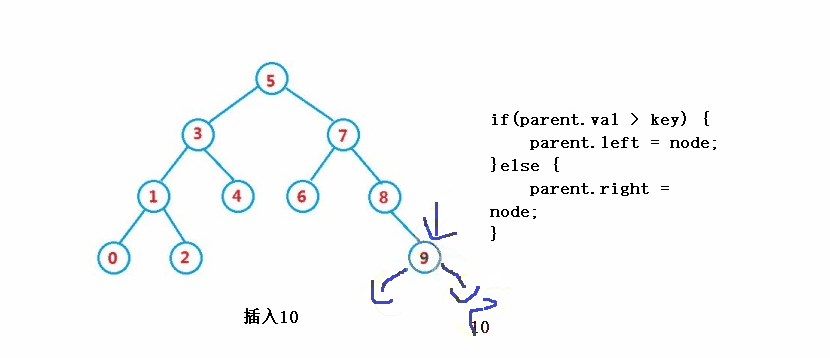
③操作 - 挿入

#

  public boolean insert(int key) {
        Node node = new Node(key);
        if(root == null) {
            root = node;
            return true;
        }
 
        Node cur = root;
        Node parent = null;
 
        while(cur != null) {
            if(cur.val == key) {
                return false;
            }else if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        //parent
        if(parent.val > key) {
            parent.left = node;
        }else {
            parent.right = node;
        }
 
        return true;
    }

④ 操作 - 削除

削除操作は比較的複雑ですが、その原理を理解するのは比較的簡単です。

削除するノードを cur とし、削除するノードの親ノードをparentとする

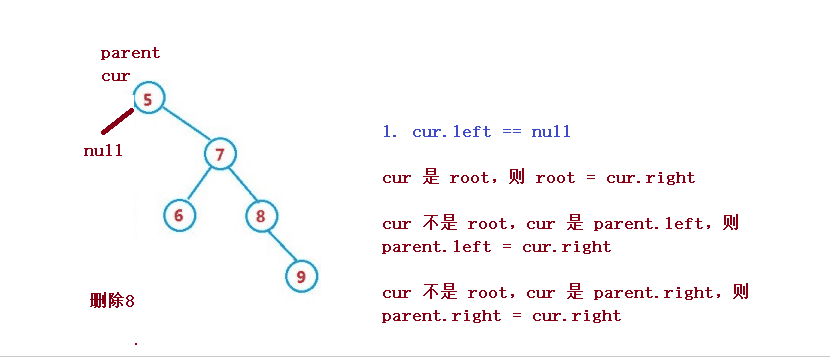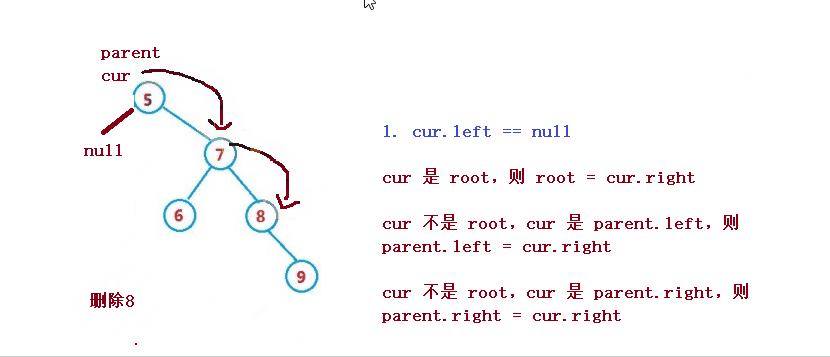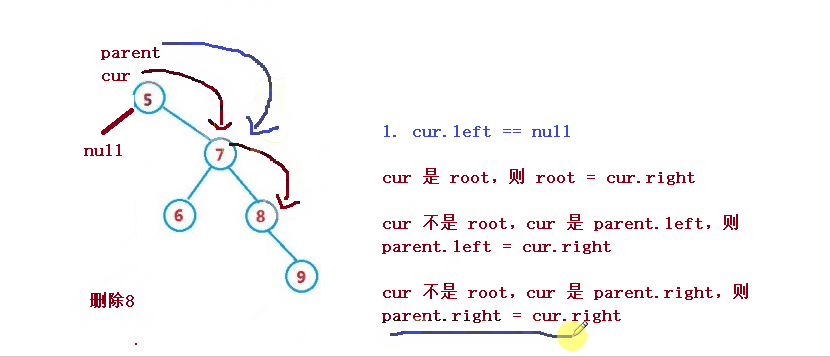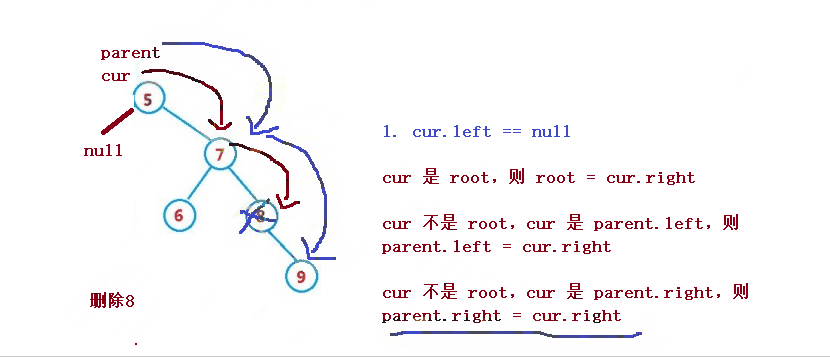
1. cur.left == null

1. cur は root、次に root = cur.right

2. cur は root ではない、cur はparent.left、そして親.left = cur.right

3. cur は root ではなく、cur はparent.rightであり、parent.right = cur.right

2. cur.right == null

1. cur が root の場合、root = cur.left

2. Cur は root ではありません、cur はparent.left、その場合はparent.left = cur.left

3. Curはrootではありません、curはparent.right、その後はparent.rightです= cur.left

2 番目のケースは、方向が逆であることを除いて最初のケースと同じであり、ここではこれ以上描画しません

3. cur.left != null && cur.right ! = null

削除するには置換メソッドを使用する必要があります。つまり、右側のサブツリーで中間の順序の最初のノード (最小のキー コード) を見つけ、その値を削除されたノードに埋めます。ノードの削除の問題

左右のサブツリーが両方とも空のときにノードを削除すると、ツリーの構造が破壊されてしまうため、スケープゴート法を使用して解決します。この場合、バイナリツリー検索のプロパティがここでも使用されます

#

public void remove(Node parent,Node cur) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }else {
            Node targetParent =  cur;
            Node target = cur.right;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }
            cur.val = target.val;
            if(target == targetParent.left) {
                targetParent.left = target.right;
            }else {
                targetParent.right = target.right;
            }
        }
    }
 
  public void removeKey(int key) {
        if(root == null) {
            return;
        }
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if(cur.val == key) {
                remove(parent,cur);
                return;
            }else if(cur.val < key){
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
    }

⑤パフォーマンス分析

挿入操作と削除操作の両方を最初に検索する必要があります。検索効率は、二分探索ツリー内の各操作のパフォーマンスを表します。

n 個のノードを持つ二分探索木の場合、各要素の検索確率が等しい場合、二分探索木の平均検索長は二分探索木のノードの深さの関数になります。つまり、ノードです。ポイントが深くなるほど、より多くの比較が行われます。

しかし、同じキー コード セットに対して、キー コードが異なる順序で挿入されると、異なる構造を持つ二分探索木が取得される可能性があります。

最適な場合、二分探索木は二分木の場合、平均比較数は次のとおりです。

最悪の場合、二分探索木は単一の分岐木に縮退し、平均比較数は次のとおりです。比較は:

⑥完整代码

public class TextDemo {
 
    public static class Node {
        public int val;
        public Node left;
        public Node right;
 
        public Node (int val) {
            this.val = val;
        }
    }
 
 
    public Node root;
 
    /**
     * 查找
     * @param key
     */
    public Node search(int key) {
        Node cur = root;
        while (cur != null) {
            if(cur.val == key) {
                return cur;
            }else if(cur.val < key) {
                cur = cur.right;
            }else {
                cur = cur.left;
            }
        }
        return null;
    }
 
    /**
     *
     * @param key
     * @return
     */
    public boolean insert(int key) {
        Node node = new Node(key);
        if(root == null) {
            root = node;
            return true;
        }
 
        Node cur = root;
        Node parent = null;
 
        while(cur != null) {
            if(cur.val == key) {
                return false;
            }else if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        //parent
        if(parent.val > key) {
            parent.left = node;
        }else {
            parent.right = node;
        }
 
        return true;
    }
 
    public void remove(Node parent,Node cur) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }else {
            Node targetParent =  cur;
            Node target = cur.right;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }
            cur.val = target.val;
            if(target == targetParent.left) {
                targetParent.left = target.right;
            }else {
                targetParent.right = target.right;
            }
        }
    }
 
    public void removeKey(int key) {
        if(root == null) {
            return;
        }
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if(cur.val == key) {
                remove(parent,cur);
                return;
            }else if(cur.val < key){
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
    }
 
}

以上がJava二分探索ツリーの追加・挿入・削除・作成例を詳しく解説の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。