Javaでブルームフィルターを実装する方法
- 王林転載
- 2023-04-24 21:43:191591ブラウズ
BitMap
現代のコンピューターは、情報の基本単位としてバイナリ (ビット、ビット) を使用します。1 バイトは 8 ビットに相当します。たとえば、bigA 文字列は 3 で構成されます。 big に対応する ASCII コードはそれぞれ 98、105、および 103 であり、対応する 2 進数はそれぞれ 01100010、01101001、および 01100111 です。
多くの開発言語にはビットを操作する機能が用意されており、ビットを適切に使用することでメモリ使用量や開発効率を効果的に向上させることができます。
ビットマップの基本的な考え方は、ビットを使用して要素に対応する値をマークすることであり、キーは要素です。データはビット単位で保存されるため、保存スペースを大幅に節約できます。
Java では、int は 4 バイト、1 バイト = 8 ビット (1 バイト = 8 ビット) を占めます。これらの 32 ビットのそれぞれの値を使用して数値を表す場合、それは数値を表すことができます。 32 個の数値。つまり、32 個の数値は int が占有するスペースだけを必要とし、スペースを 32 分の 1 に削減できます。
1 バイト = 8 ビット、1 KB = 1024 バイト、1 MB = 1024 KB、1GB = 1024 MB
Web サイトに 1 億人のユーザーがアクセスすると仮定します。毎日独立してユーザーが 5,000 万人います。コレクション タイプと BitMap を使用してアクティブ ユーザーを毎日保存する場合:
1. ユーザー ID が int 型、4 バイト、32 ビットの場合、コレクション タイプが占有します50,000 個のスペース。000 * 4/1024/1024 = 200M;
2。ビットで保存した場合、5,000 万個の数値は 5,000 万ビットで、占有スペースは 50 000 000/8/1024/1024 = 6M です。 。
では、BitMap を使用して数値を表すにはどうすればよいでしょうか?
上で述べたように、ビット ビットは要素に対応する値をマークするために使用され、キーは要素です。BitMap はビット単位の 配列 として想像できます。各ユニットは 0 と 1 のみを格納できます (0 はその数値が存在しないことを意味し、1 はその数値が存在することを意味します)。配列の添字は BitMap ではオフセットと呼ばれます。たとえば、4 つの数値 {1,3,5,7} を次のように表す必要があります:
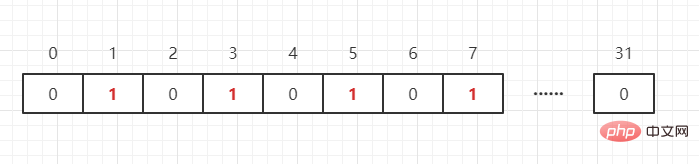
別の数値 65 がある場合はどうなるでしょうか。 ?これらのデータを保存するには、int[N/32 1] int 配列を開くだけで済みます (N は、このデータ グループの最大値を表します)。つまり、
int [0]: 0 ～ 31
int[1]: 32 ～ 63
int[2]## を表すことができます。 # : 64 ～ 95 を表すことができます
M/32 は添字を取得します。 M2 は、
65/32 = 2、652=1 など、この添え字のどこにあるかを認識します。つまり、 65 は int[2] の最初のビットにあります。
ウェブページブラックリストシステム、スパムフィルタリングシステム、クローラーURL重み判定システムなどで広く使用されています。 Google の有名な分散データベース Bigtable は、ブルーム フィルタを使用して存在しない行や列を見つけ、IO ディスク検索の数を減らします。Google Chrome ブラウザはブルーム フィルタを使用して、安全なブラウジング サービスを高速化します。
ブルーム フィルターは、Hbase、Accumulo、Leveldb などのクエリ プロセスを高速化するために、多くの Key-Value システムでも使用されます。一般に、値はディスクに保存され、ディスクへのアクセスには大量の時間がかかります。ただし、ブルーム フィルターを使用すると、キーに対応する値が存在するかどうかを迅速に判断できるため、多くの不要なディスク IO 操作を回避できます。 ハッシュ関数を使用して、要素をビット配列 (ビット配列) 内の点にマッピングします。このように、点がセット内にあるかどうかを知るためには、点が 1 であるかどうかを確認するだけで済みます。これがブルームフィルターの基本的な考え方です。 アプリケーション シナリオ 1. 現在、無秩序に配置された 10 億個の自然数があり、それらを並べ替える必要があります。この制限は 32 ビット マシンに実装されており、メモリ制限は 2G です。どのように行われるのでしょうか？ 2. URL アドレスがブラックリストに含まれているかどうかをすばやく確認するにはどうすればよいですか? (各 URL は平均 64 バイトです)3. ユーザーのアクティビティを判断するために、ユーザーのログイン動作を分析する必要がありますか? 4. Web クローラー - URL がクロールされたかどうかを確認するにはどうすればよいですか? 5. ユーザー属性 (ブラックリスト、ホワイトリストなど) をすばやく見つけますか? 6. データはディスクに保存されますが、大量の無効な IO を回避するにはどうすればよいですか? 7. 数十億のデータに要素が存在するかどうかを判断しますか? 8. キャッシュの侵入。従来のデータ構造の欠点
一般に、Web ページの URL を検索用にデータベースに保存するか、検索用のハッシュ テーブルを作成しても問題ありません。
データ量が少ない場合は、このように考えるのが正しいですが、実際に HashMap のキーに値をマッピングすると、O(1) 時間以内に結果を返すことができます。非常に効率的です。ただし、HashMapの実装には、ストレージ容量の割合が高いなどの欠点もあり、負荷要因の存在を考慮すると、通常、スペースを使い切ることができません。たとえば、1,000万のHashMapの場合、Key=String(長さが一致しない) 16 文字を超え、再現性はほとんどありません）、値 = 整数、どのくらいのスペースを占有しますか? 1.2G。
実際にビットマップを使用すると、1,000 万の int 型には約 4,000 万 (10 000 000 * 4/1024/1024 = 40M) のスペースが必要であり、3% を占めます。1,000 万の Integer は約 161M のスペースを必要とし、13.3 を占めます。 %。
数億などの多くの値を取得すると、HashMap が占有するメモリ サイズが想像できることがわかります。
しかし、Web ページ ブラックリスト システム全体に 100 億の Web ページ URL が含まれている場合、データベース内の検索には非常に時間がかかり、各 URL スペースが 64B の場合、640GB のメモリが必要となり、これは通常のサーバーでは困難です。達成する必要がある。
実装原則
集合 A があり、A には n 個の要素があるとします。 k ハッシュ ハッシュ 関数を使用して、A の各要素 を配列 B の異なる位置にビット長でマップします。これらの位置の 2 進数は両方とも 1 に設定されます。チェック対象の要素がこれらの k 個のハッシュ関数によってマッピングされ、その k 位置の 2 進数 がすべて 1 であることが判明した場合、この要素は集合 A に属する可能性が高くなります。それ以外の場合、セット A に属してはなりません。
たとえば、3 つの URL{URL1,URL2,URL3} があり、次のようにハッシュ関数を通じて長さ 16 の配列にマップします。
現在のハッシュ関数が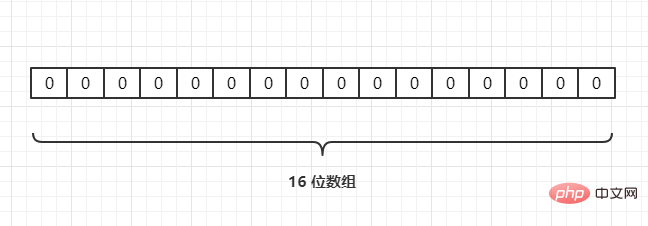 
Hash2()
Hash2(URL1) = 3 と仮定して、ハッシュ演算を通じて配列にマッピングされます。 Hash2(URL2) = 6, Hash2(URL3) = 6、次のように:
したがって、次のように判断する必要がある場合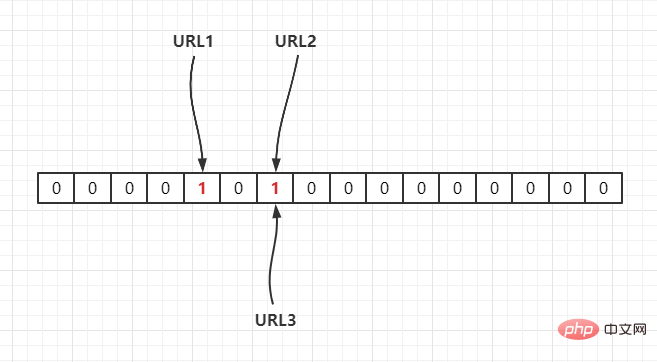
URL1
Hash(1) を通じてその添え字を計算し、その値を取得します。1 であれば、それが存在することを意味します。 Hash でのハッシュの競合により、上に示したように、URL2、URL3
1% に削減したい場合、このハッシュ テーブルは m/100 要素のみを収容できます。明らかに、スペース使用率は次のようになります。 スペース効果的な (スペース効率の良い) にします。 解決策も簡単です。つまり、複数のハッシュ アルゴリズムを使用します。そのうちの 1 つが要素がセット内にないと言う場合、次のように、要素は間違いなくそこにありません:
Hash2(URL1) = 3,Hash3(URL1) = 5,Hash4(URL1) = 6 Hash2(URL2) = 5,Hash3(URL2) = 8,Hash4(URL2) = 14 Hash2(URL3) = 4,Hash3(URL3) = 7,Hash4(URL3) = 10
誤判定現象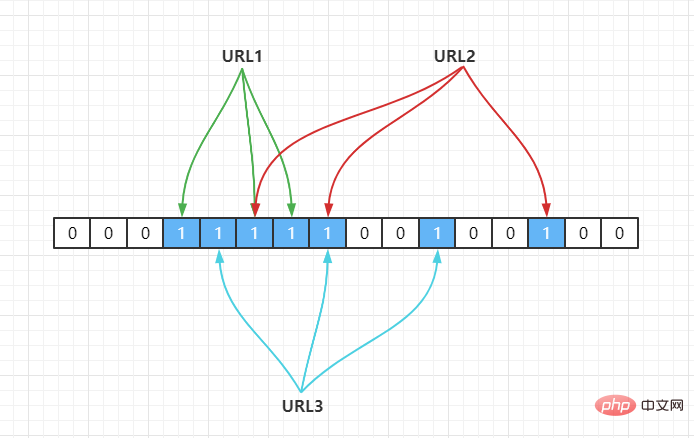
URL1000
が来ますが、ハッシュ計算すると次のようなビットであることがわかります。URL1、URL2、URL3 によって 1 に設定されますが、この時点でプログラムは URL1000
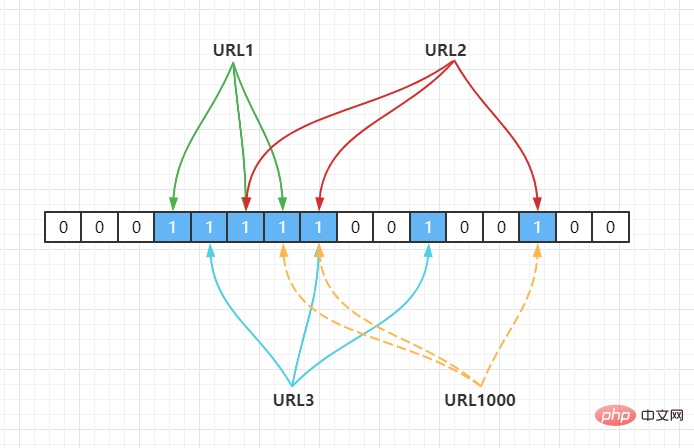これはブルームフィルタの誤判定現象ですので、
ブルーム フィルターはセットを正確に表現し、要素がこのセットに含まれるかどうかを正確に判断できます。精度はユーザーの特定の設計によって決まります。100% の精度を達成することは不可能です。しかし、ブルーム フィルターの利点は、非常に少ないスペースでより高い精度を達成できることです。 実装
Redis のビットマップRedis のビットマップ データ構造の関連命令に基づいて実行されます。
RedisBloom ブルームフィルターは、Redis のビットマップ操作を使用して実装できます。Redis が正式に提供するブルームフィルターが正式にオンになったのは、Redis 4.0 バージョンでプラグイン機能が提供されてからです。シーンでは、ブルーム フィルターは Redis Server にプラグインとして読み込まれますが、公式 Web サイトでは、Redis Bloom フィルターのモジュールとして RedisBloom を推奨しています。
Guava の BloomFilter
Guava プロジェクトがバージョン 11.0 をリリースしたとき、新しく追加された機能の 1 つが BloomFilter クラスでした。
Redisson
Redisson は、ビットマップに基づいてブルーム フィルターを実装します。
public static void main(String[] args) {
Config config = new Config();
// 单机环境
config.useSingleServer().setAddress("redis://192.168.153.128:6379");
//构造Redisson
RedissonClient redisson = Redisson.create(config);
RBloomFilter<String> bloomFilter = redisson.getBloomFilter("nameList");
//初始化布隆过滤器：预计元素为100000000L,误差率为3%,根据这两个参数会计算出底层的 bit 数组大小
bloomFilter.tryInit(100000L, 0.03);
//将 10086 插入到布隆过滤器中
bloomFilter.add("10086");
//判断下面号码是否在布隆过滤器中
System.out.println(bloomFilter.contains("10086"));//true
System.out.println(bloomFilter.contains("10010"));//false
System.out.println(bloomFilter.contains("10000"));//false
}解决缓存穿透
缓存穿透是指查询一个根本不存在的数据，缓存层和存储层都不会命中，如果从存储层查不到数据则不写入缓存层。
缓存穿透将导致不存在的数据每次请求都要到存储层去查询，失去了缓存保护后端存储的意义。缓存穿透问题可能会使后端存储负载加大，由于很多后端存储不具备高并发性，甚至可能造成后端存储宕掉。
因此我们可以用布隆过滤器来解决，在访问缓存层和存储层之前，将存在的 key 用布隆过滤器提前保存起来，做第一层拦截。
例如：一个推荐系统有 4 亿个用户 id，每个小时算法工程师会根据每个用户之前历史行为计算出推荐数据放到存储层中，但是最新的用户由于没有历史行为，就会发生缓存穿透的行为，为此可以将所有推荐数据的用户做成布隆过滤器。如果布隆过滤器认为该用户 id 不存在，那么就不会访问存储层，在一定程度保护了存储层。
注：布隆过滤器可能会误判，放过部分请求，当不影响整体，所以目前该方案是处理此类问题最佳方案
以上がJavaでブルームフィルターを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。