Javaで無向グラフを実装するにはどうすればよいですか?

#基本概念

グラフの定義

グラフは点集合 V={v

i## で構成されます#} VV 内の順序のない要素のペアのセット E={e_k} で構成されるタプルは G=(V,E) として記録され、V 内の要素 v_{i## は #を頂点と呼び、E の要素 e}k _{をエッジと呼びます。 V の 2 点 u, v について、エッジ (u, v) が E に属している場合、2 点 u と v は隣接しているとみなされ、u と v は端点と呼ばれます。エッジ (u, v) 。}

m(G)=|E| を使用してグラフ G のエッジの数を表し、n(G)=|V| を使用してグラフ G の頂点の数を表すことができます。

無向グラフの定義

E の任意の辺 (vi, vj) ​​について、辺 (vi, vj) ​​の端点が順序付けされていない場合、それは無向辺です。グラフ G は無向グラフと呼ばれます。無向グラフは最も単純なグラフ モデルです。次の図は、同じ無向グラフを示しています。頂点は円で表され、エッジは矢印のない頂点間の接続です (図は「アルゴリズム第 4 版」から):

無向グラフの API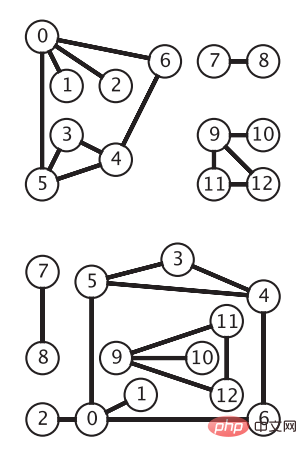

無向グラフの場合、頂点の数、エッジの数、各頂点の隣接する頂点の合計、およびエッジの追加を考慮します。

package com.zhiyiyo.graph;

/**
 * 无向图
 */
public interface Graph {
    /**
     * 返回图中的顶点数
     */
    int V();

    /**
     * 返回图中的边数
     */
    int E();

    /**
     * 向图中添加一条边
     * @param v 顶点 v
     * @param w 顶点 w
     */
    void addEdge(int v, int w);

    /**
     * 返回所有相邻顶点
     * @param v 顶点 v
     * @return 所有相邻顶点
     */
    Iterable<Integer> adj(int v);
}

無向グラフの実装方法

隣接行列

行列を使ってグラフを表現することは、性質や性質を調べるためによく使われます。グラフの応用 より便利になります 各種グラフには重み行列や隣接行列などさまざまな行列の表現方法がありますが、ここでは隣接行列のみに焦点を当てます。これは次のように定義されます:

グラフ G=(V,E), |V|=n の場合、行列 A=(a

ij

)

n×n## を構築します。 # 、ここで:

# 次に、行列 A はグラフ G の隣接行列と呼ばれます。

定義から、2 次元ブール配列

A

を使用して隣接行列を実装できることがわかります。 # では、頂点

i

と j が隣接しています。 n 個の頂点を持つグラフ G の場合、隣接行列によって消費されるスペースは n2 ブール値のサイズであり、スパース グラフでは多くの無駄が発生します。頂点の数が非常に大きい場合、消費されるスペースは天文学的な数字になります。同時に、グラフが特殊で、自己ループと平行エッジを持つ場合、隣接行列表現は無力になります。 「アルゴリズム」では、次の 2 つの状況のグラフが得られます。

^{#エッジの配列}

無向グラフの場合、クラス

Edge## を実装できます。 # では、2 つの頂点 u と v を格納するために 2 つのインスタンス変数のみが使用され、すべての 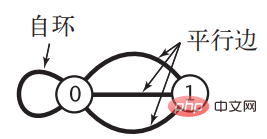Edge

を配列に保存できます。これには大きな問題があります。つまり、頂点 v のすべての隣接する頂点を取得する場合、配列全体を走査してそれらを取得する必要があります。時間計算量は O(|E|) です。隣接する頂点の取得は非常に一般的な操作であるため、 , この表現方法もダメです。

隣接リスト配列

値の範囲が 0∼|V|−1 の整数として頂点を表す場合、長さ |V| の配列を使用できます。は各頂点を表し、各配列要素はインデックスで表される頂点に隣接する他の頂点がマウントされるリンク リストに設定されます。図 1 に示す無向グラフは、次の図に示す隣接リスト配列で表すことができます。

隣接リストを使用して無向グラフを実装するコードは次のとおりです。隣接リスト配列内の各リンク リストは頂点に隣接する頂点を保存するため、グラフにエッジを追加するときは、配列内の 2 つのリンク リストにノードを追加する必要があります。スタック コードは次のとおりです。スタックの実装はこのブログの焦点では​​ないため、ここではあまり説明しません:

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.stack.LinkStack;

/**
 * 使用邻接表实现的无向图
 */
public class LinkGraph implements Graph {
    private final int V;
    private int E;
    private LinkStack<Integer>[] adj;

    public LinkGraph(int V) {
        this.V = V;
        adj = (LinkStack<Integer>[]) new LinkStack[V];
        for (int i = 0; i < V; i++) {
            adj[i] = new LinkStack<>();
        }
    }

    @Override
    public int V() {
        return V;
    }

    @Override
    public int E() {
        return E;
    }

    @Override
    public void addEdge(int v, int w) {
        adj[v].push(w);
        adj[w].push(v);
        E++;
    }

    @Override
    public Iterable<Integer> adj(int v) {
        return adj[v];
    }
}

無向グラフの走査

次の図では、各頂点から頂点 0 までのパスを見つける必要があります。これを実現するにはどうすればよいでしょうか?簡単に言うと、頂点 0 と 4 が与えられた場合、頂点 0 から開始して頂点 4 に到達できるかどうかを判断する必要があります。これを実現するにはどうすればよいでしょうか?これには、深さ優先検索と幅優先検索という 2 つのグラフ走査方法を使用する必要があります。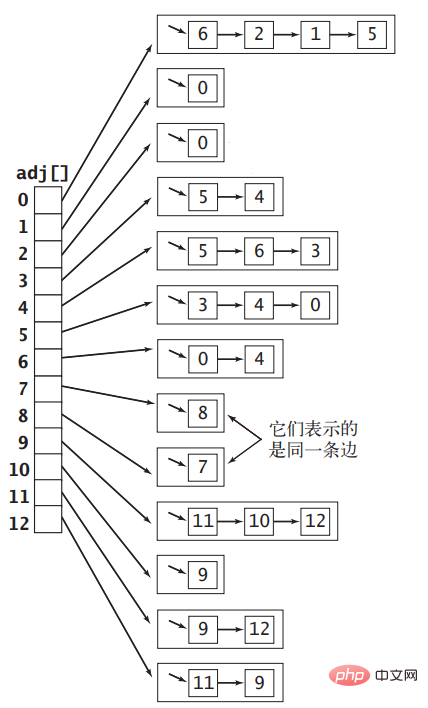

これら 2 つのトラバーサル メソッドを紹介する前に、まず、上記の問題を解決するために実装する必要がある API を示します。

package com.zhiyiyo.graph;

public interface Search {
    /**
     * 起点 s 和 顶点 v 之间是否连通
     * @param v 顶点 v
     * @return 是否连通
     */
    boolean connected(int v);

    /**
     * 返回与顶点 s 相连通的顶点个数（包括 s）
     */
    int count();

    /**
     * 是否存在从起点 s 到顶点 v 的路径
     * @param v 顶点 v
     * @return 是否存在路径
     */
    boolean hasPathTo(int v);

    /**
     * 从起点 s 到顶点 v 的路径，不存在则返回 null
     * @param v 顶点 v
     * @return 路径
     */
    Iterable<Integer> pathTo(int v);
}

深度优先搜索

深度优先搜索的思想类似树的先序遍历。我们从顶点 0 开始，将它的相邻顶点 2、1、5 加到栈中。接着弹出栈顶的顶点 2，将它相邻的顶点 0、1、3、4 添加到栈中，但是写到这你就会发现一个问题：顶点 0 和 1明明已经在栈中了，如果还把他们加到栈中，那这个栈岂不是永远不会变回空。所以还需要维护一个数组 boolean[] marked，当我们将一个顶点 i 添加到栈中时，就将 marked[i] 置为 true，这样下次要想将顶点 i 加入栈中时，就得先检查一个 marked[i] 是否为 true，如果为 true 就不用再添加了。重复栈顶节点的弹出和节点相邻节点的入栈操作，直到栈为空，我们就完成了顶点 0 可达的所有顶点的遍历。

为了记录每个顶点到顶点 0 的路径，我们还需要一个数组 int[] edgeTo。每当我们访问到顶点 u 并将其一个相邻顶点 i 压入栈中时，就将 edgeTo[i] 设置为 u，说明要想从顶点i 到达顶点 0，需要先回退顶点 u，接着再从顶点 edgeTo[u] 处获取下一步要回退的顶点直至找到顶点 0。

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.stack.LinkStack;
import com.zhiyiyo.collection.stack.Stack;


public class DepthFirstSearch implements Search {
    private boolean[] marked;
    private int[] edgeTo;
    private Graph graph;
    private int s;
    private int N;

    public DepthFirstSearch(Graph graph, int s) {
        this.graph = graph;
        this.s = s;
        marked = new boolean[graph.V()];
        edgeTo = new int[graph.V()];
        dfs();
    }

    /**
     * 递归实现的深度优先搜索
     *
     * @param v 顶点 v
     */
    private void dfs(int v) {
        marked[v] = true;
        N++;
        for (int i : graph.adj(v)) {
            if (!marked[i]) {
                edgeTo[i] = v;
                dfs(i);
            }
        }
    }

    /**
     * 堆栈实现的深度优先搜索
     */
    private void dfs() {
        Stack<Integer> vertexes = new LinkStack<>();
        vertexes.push(s);
        marked[s] = true;

        while (!vertexes.isEmpty()) {
            Integer v = vertexes.pop();
            N++;

            // 将所有相邻顶点加到堆栈中
            for (Integer i : graph.adj(v)) {
                if (!marked[i]) {
                    edgeTo[i] = v;
                    marked[i] = true;
                    vertexes.push(i);
                }
            }
        }
    }

    @Override
    public boolean connected(int v) {
        return marked[v];
    }

    @Override
    public int count() {
        return N;
    }

    @Override
    public boolean hasPathTo(int v) {
        return connected(v);
    }

    @Override
    public Iterable<Integer> pathTo(int v) {
        if (!hasPathTo(v)) return null;
        Stack<Integer> path = new LinkStack<>();

        int vertex = v;
        while (vertex != s) {
            path.push(vertex);
            vertex = edgeTo[vertex];
        }

        path.push(s);
        return path;
    }
}

广度优先搜索

广度优先搜索的思想类似树的层序遍历。与深度优先搜索不同，从顶点 0 出发，广度优先搜索会先处理完所有与顶点 0 相邻的顶点 2、1、5 后，才会接着处理顶点 2、1、5 的相邻顶点。这个搜索过程就是一圈一圈往外扩展、越走越远的过程，所以可以用来获取顶点 0 到其他节点的最短路径。只要将深度优先搜索中的堆换成队列，就能实现广度优先搜索：

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.queue.LinkQueue;

public class BreadthFirstSearch implements Search {
    private boolean[] marked;
    private int[] edgeTo;
    private Graph graph;
    private int s;
    private int N;

    public BreadthFirstSearch(Graph graph, int s) {
        this.graph = graph;
        this.s = s;
        marked = new boolean[graph.V()];
        edgeTo = new int[graph.V()];
        bfs();
    }

    private void bfs() {
        LinkQueue<Integer> queue = new LinkQueue<>();
        marked[s] = true;
        queue.enqueue(s);

        while (!queue.isEmpty()) {
            int v = queue.dequeue();
            N++;

            for (Integer i : graph.adj(v)) {
                if (!marked[i]) {
                    edgeTo[i] = v;
                    marked[i] = true;
                    queue.enqueue(i);
                }
            }
        }
    }
}

队列的实现代码如下：

package com.zhiyiyo.collection.queue;


import java.util.EmptyStackException;


public class LinkQueue<T> {
    private int N;
    private Node first;
    private Node last;

    public void enqueue(T item) {
        Node node = new Node(item, null);
        if (++N == 1) {
            first = node;
        } else {
            last.next = node;
        }
        last = node;
    }

    public T dequeue() throws EmptyStackException {
        if (N == 0) {
            throw new EmptyStackException();
        }

        T item = first.item;
        first = first.next;
        if (--N == 0) {
            last = null;
        }
        return item;
    }

    public int size() {
        return N;
    }

    public boolean isEmpty() {
        return N == 0;
    }

    private class Node {
        T item;
        Node next;

        public Node() {
        }

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }
}

以上がJavaで無向グラフを実装するにはどうすればよいですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。