SARIMA、XGBoost、CNN-LSTM に基づく時系列予測方法を比較します。

統計テストと機械学習を使用した太陽光発電の分析と予測のパフォーマンス テストと比較

この記事では、仮説テスト、特徴エンジニアリング、時系列を使用してデータセットから具体的な値を取得する手法について説明しますモデリング方法など。また、データ漏洩やさまざまな時系列モデルのデータ準備などの問題にも対処し、3 つの一般的な時系列予測の比較テストを実施します。

はじめに

時系列予測はよく研究されるテーマですが、ここでは 2 つの太陽光発電所のデータを使用して、その法則を調べ、モデリングを行います。これらの問題は、まず 2 つの質問に要約して解決してください:

1. パフォーマンスの低いソーラー モジュールを特定することは可能ですか?
2. 2日間の太陽光発電量を予測することは可能ですか?

これらの質問に答える前に、まず太陽光発電所がどのように発電するかを理解しましょう。

#上の図は、ソーラー パネル モジュールからグリッドまでの発電プロセスを示しています。太陽エネルギーは、光電効果によって直接電気エネルギーに変換されます。シリコンなどの材料 (ソーラー パネルで最も一般的な半導体材料) が光にさらされると、光子 (電磁エネルギーの素粒子) が吸収され、自由電子が放出されて、直流 (DC) が生成されます。インバーターを使用すると、DC 電力が交流 (AC) に変換され、電力網に送られ、家庭に配電できます。

データ

生データは、各太陽光発電所の 2 つのカンマ区切り値 (CSV) ファイルで構成されます。 1 つの文書には発電プロセスが示され、もう 1 つの文書には太陽光発電所のセンサーによって記録された測定値が示されています。各太陽光発電所の 2 つのデータセットは、pandas df に編成されました。

太陽光発電所 1 (SP1) と太陽光発電所 2 (SP2) からのデータは、2020 年 5 月 15 日から 2020 年 6 月 18 日まで 15 分ごとに収集されました。 SP1 と SP2 の両方のデータセットには同じ変数が含まれています。

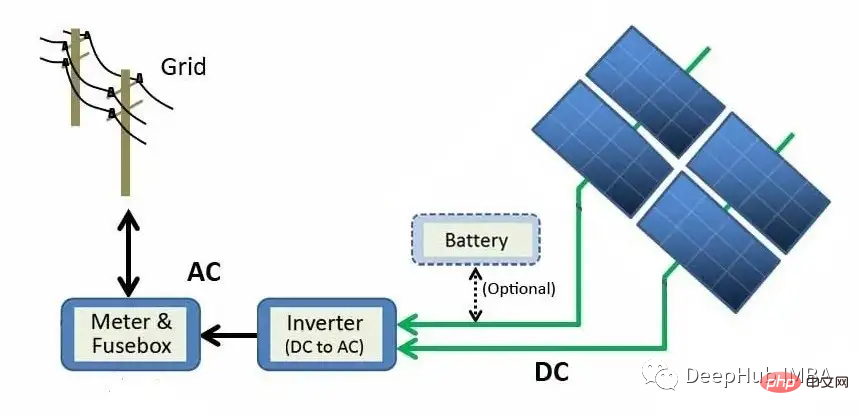
日付時刻 - 15 分間隔
• 周囲温度 - モジュール周囲の空気の温度
• モジュール温度 - モジュールの温度
• 照射—— モジュール上の放射線
• DC 電力 (kW) - 直流
• AC 電力 (kW) - AC
• 1 日あたりの発電量 - 1 日あたりの合計電力世代
• 合計発電量 - インバーターの累積発電量
• プラント ID - 太陽光発電所の一意の識別
• モジュール ID - 各モジュールの一意の識別

気象センサー用 各太陽光発電所の周囲温度、モジュール温度、日射量を記録します。

このデータセットでは、DC 電力が従属変数 (ターゲット変数) になります。私たちの目標は、性能の低い太陽電池モジュールを見つけ出すことです。

2 つの独立した DF が分析と予測に使用されます。唯一の違いは、予測に使用されるデータは 1 時間間隔にリサンプリングされるのに対し、分析に使用されるデータ フレームには 15 分間隔が含まれることです。

まず、上記の質問に答えようとしても何の価値もないので、プラント ID を削除します。モジュール ID も予測データセットから削除されます。表 1 および表 2 にデータ例を示します。

##データの分析を続ける前に、太陽光発電所について次のような仮定を立てました。 # #データ収集装置には障害はありません #モジュールは定期的に清掃されています (メンテナンスの影響を無視)

#2 つの太陽光発電所の周囲に閉塞の問題はありません

探索的データ分析 (EDA)
• データ サイエンスの初心者にとって、EDA は、視覚化をプロットし、統計テストを実行することでデータを理解するための重要なステップです。まず、SP1 と SP2 の DC と AC をプロットすることで、各太陽光発電所のパフォーマンスを観察できます。

SP1 は、sp2 よりも 1 桁高い DC 電力を示します。 SP1 によって収集されたデータが正しく、データの記録に使用された機器に欠陥がないと仮定すると、SP1 のインバータにはさらに詳細な調査が必要であることを意味します。

図 3 は、毎日の頻度で各モジュールの AC 電力と DC 電力を合計したもので、SP1 のすべてのモジュールのインバータ効率を示しています。この分野の知識によれば、太陽光発電インバーターの効率は 93 ～ 96% である必要があります。すべてのモジュールの効率は 9.76% ～ 9.79% の範囲であるため、これはインバータの性能を調査し、交換する必要があるかどうかを調査する必要があることを示しています。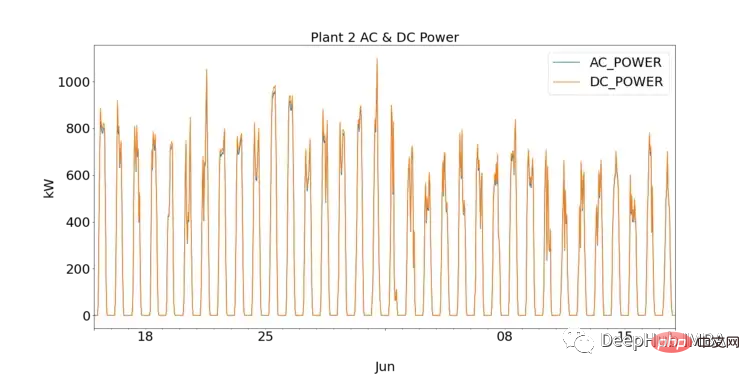

SP1 ではインバーターに問題があったため、SP2 についてのみさらなる分析が行われました。

この短い分析は、インバーターの研究に多くの時間を費やした結果ですが、太陽電池モジュールの性能を判断するという主要な質問には答えていません。

SP2 のインバーターは正常に機能しているため、データを深く掘り下げることで異常を特定し、調査できます。

図4にモジュール温度と周囲温度の関係を示しますが、モジュール温度が非常に高くなる場合があります。

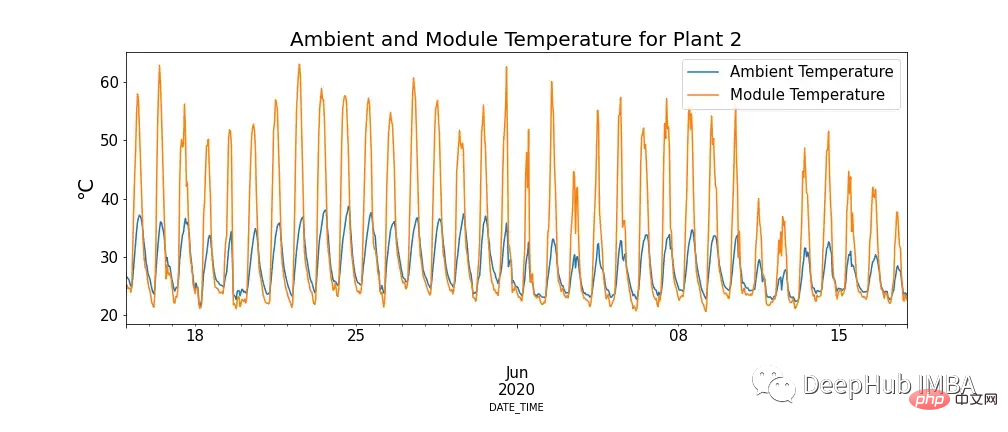
これは私たちの知識に反するようですが、高温がソーラーパネルに悪影響を与えることは明らかです。光子が太陽電池内の電子と接触すると、自由電子が放出されますが、高温ではより多くの電子がすでに励起状態にあり、パネルが生成できる電圧が低下し、効率が低下します。

この現象を念頭に置いて、以下の図 5 に SP2 のモジュール温度と DC 電力を示します (周囲温度がモジュール温度より低いデータ ポイントと、モジュールが低い数値で動作している時間帯)データの偏りを防ぐためにフィルタリングされています)。

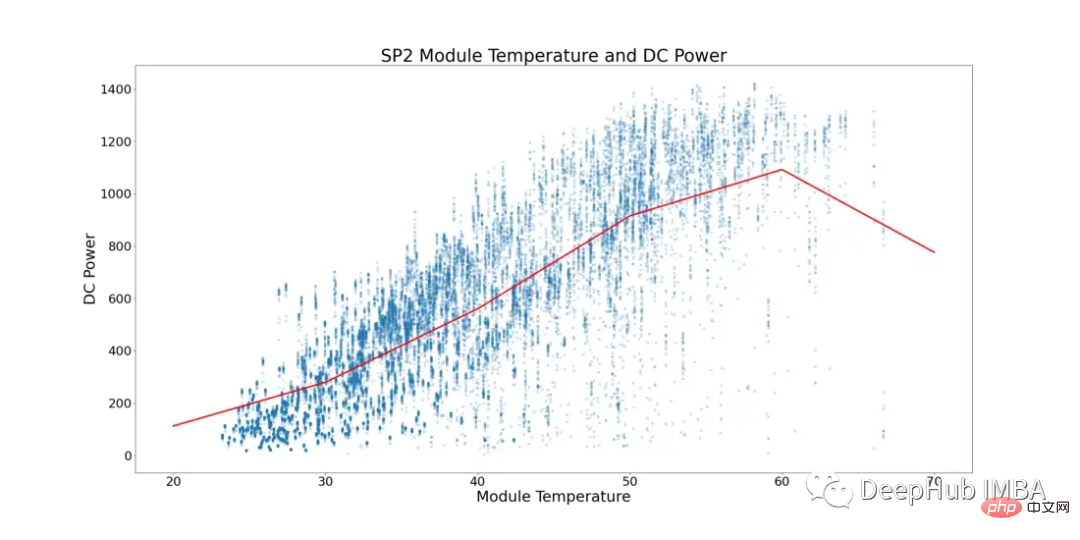
図 5 では、赤い線は平均気温を表しています。ここでは、明らかな転換点と DC 電力停滞の兆候があることがわかります。 ~52°C でプラトー状態が始まります。性能が最適ではない太陽電池モジュールを見つけるために、モジュール温度が 52°C を超える行をすべて削除しました。

以下の図 6 は、1 日にわたる SP2 の各モジュールの DC 電力を示しています。これは基本的に期待通りであり、正午の発電量が大きくなります。しかし、別の問題があり、ピーク運転時間帯には発電量が低下します。その日の天候が悪かったり、SP2 の定期的なメンテナンスが必要になったりする可能性があるため、この状況の理由を要約することは困難です。

図 6 には、低パフォーマンスのモジュールの兆候もあります。それらは、最も近いクラスターから逸脱するグラフ上のモジュール (個々のデータ ポイント) として識別できます。

どのモジュールのパフォーマンスが低いかを判断するには、各モジュールのパフォーマンスを他のモジュールと比較しながら統計テストを実行してパフォーマンスを判断できます。

15 分ごとに、同時に異なるモジュールの DC 電源の分布は正規分布になります。仮説検証を通じて、どのモジュールのパフォーマンスが低いかを特定できます。カウントは、モジュールが p 値

図 7 は、同じ期間中に各モジュールが他のモジュールよりも統計的に有意に低かった回数を降順に示しています。

図 7 から、モジュール「Quc1TzYxW2pYoWX」に問題があることは明らかです。この情報は、原因を調査するために関連する SP2 スタッフに提供できます。

モデリング

以下では、SARIMA、XGBoost、および CNN-LSTM の 3 つの異なる時系列アルゴリズムを使用してモデル化および比較を開始します。

3 つのモデルすべてで、次の予測を使用します。予測用のデータポイント。ウォークフォワード検証は、時間の経過とともに予測の精度が低下するため、時系列モデリングで使用される手法です。そのため、より実用的なアプローチは、実際のデータが利用可能になったときにモデルを再トレーニングすることです。

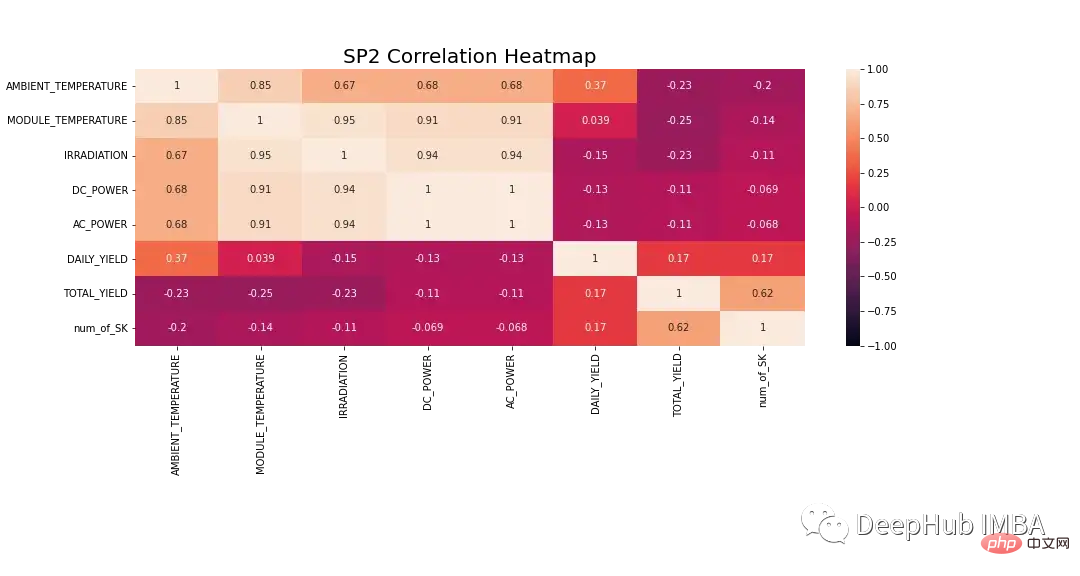
モデル化する前に、データをより詳細に調査する必要があります。図 8 は、SP2 データセット内のすべてのフィーチャの相関ヒートマップを示しています。ヒート マップは、従属変数である DC 電力とモジュール温度、日射量、周囲温度との強い相関関係を示しています。これらの特性は、予測において重要な役割を果たす可能性があります。

以下のヒート マップでは、AC 電力はピアソン相関係数 1 を示しています。データ漏洩の問題を防ぐために、データから DC 電源を除去します。

SARIMA

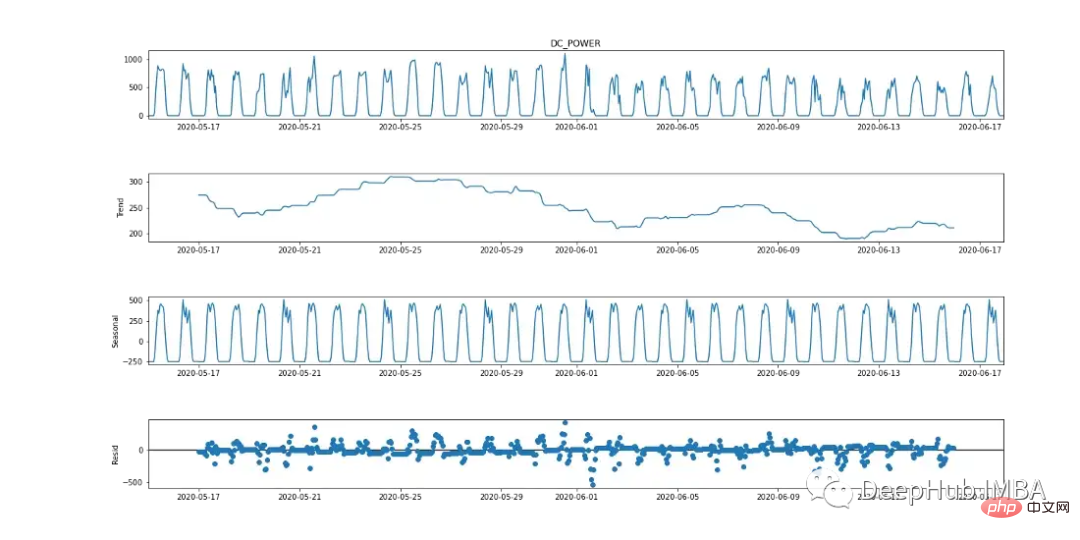
季節自己回帰統合移動平均 (SARIMA) は、単変量時系列予測手法です。ターゲット変数は 24 時間周期の兆候を示しているため、SARIMA は季節の影響を考慮した効率的なモデリング オプションです。これは、以下の季節内訳グラフで確認できます。

#SARIMA アルゴリズムでは、データが定常であることが必要です。データが定常であるかどうかをテストするには、統計検定 (拡張ディッキー・ファウラー検定)、要約統計 (データのさまざまな部分の平均/分散の比較)、データの視覚的分析など、さまざまな方法があります。モデリングの前に複数のテストを実行することが重要です。

拡張ディッキー フラー (ADF) テストは、時系列が定常であるかどうかを判断するために使用される「単位根テスト」です。基本的に、これは帰無仮説と対立仮説が存在し、結果の p 値に基づいて結論が導き出される統計的有意性検定です。

帰無仮説: 時系列データは非定常です。

対立仮説: 時系列データは定常です。

この例では、p 値 ≤ 0.05 の場合、帰無仮説を棄却し、データに単位根がないことを確認できます。

 from statsmodels.tsa.stattools import adfuller
 
 result = adfuller(plant2_dcpower.values)
 
 print('ADF Statistic: %f' % result[0])
 print('p-value: %f' % result[1])
 print('Critical Values:')
 for key, value in result[4].items():
print('t%s: %.3f' % (key, value))

ADF テストから、p 値は 0.000553、

SARIMA を使用して従属変数をモデル化するには、時系列が定常である必要があります。図 9 (1 番目と 3 番目のグラフ) に示すように、DC 電力には季節性の明らかな兆候があります。図 10 に示すように、最初の差分 [t-(t-1)] を取得して季節成分を除去します。これは正規分布に似ているためです。データは固定されており、SARIMA アルゴリズムに適しています。

SARIMA のハイパーパラメータには、p (自己回帰次数)、d (差分次数)、q (移動平均次数)、p (季節的自己回帰次数)、d (季節次数) が含まれます。差）、q（季節移動平均の次数）、m（季節サイクルの時間ステップ）、trend（決定的な傾向）。

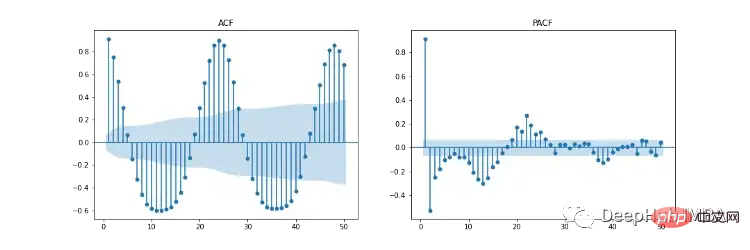
図 11 は、自己相関 (ACF)、偏自己相関 (PACF)、および季節 ACF/PACF プロットを示しています。 ACF プロットは、時系列とその遅延バージョンの間の相関関係を示します。 PACF は、時系列とその遅延バージョンの間の直接的な相関関係を示します。青い影付きの領域は信頼区間を表します。 SACF と SPACF は、元のデータから季節差 (m) を取得することによって計算できます。ACF プロットには明らかな 24 時間の季節効果があるため、この場合は 24 です。

私たちの直感によれば、ハイパーパラメーターの開始点は ACF グラフと PACF グラフから導き出すことができます。たとえば、ACF と PACF はどちらも緩やかな下降傾向を示します。つまり、自己回帰次数 (p) と移動平均次数 (q) は両方とも 0 より大きくなります。 p と p は、それぞれ PCF と SPCF プロットを調べ、ラグ値が有意でなくなる前に統計的に有意になるラグの数を数えることによって決定できます。同様に、q と q は ACF ダイアグラムと SACF ダイアグラムで見つけることができます。

差分の次数 (d) は、データを定常にする差分の数によって決定できます。季節差次数 (D) は、時系列から季節成分を除去するために必要な差分の数から推定されます。

これらのハイパーパラメータの選択については、この記事を参照してください: https://arauto.readthedocs.io/en/latest/how_to_choose_terms.html

ハイパーパラメータの最適化にグリッド検索方法を使用することもできます、最小平均二乗誤差 (MSE) に基づいて最適なハイパーパラメータを選択します。これには、p = 2、d = 0、q = 4、p = 2、d = 1、q = 6、m = 24、trend = ' n ' が含まれます。 (トレンドなし)。

from time import time
 from sklearn.metrics import mean_squared_error
 from statsmodels.tsa.statespace.sarimax import SARIMAX
 
 configg = [(2, 1, 4), (2, 1, 6, 24), 'n']
 
 def train_test_split(data, test_len=48):
"""
Split data into training and testing.
"""
train, test = data[:-test_len], data[-test_len:]
return train, test
 
 def sarima_model(data, cfg, test_len, i):
"""
SARIMA model which outputs prediction and model.
"""
order, s_order, t = cfg[0], cfg[1], cfg[2]
model = SARIMAX(data, order=order, seasonal_order=s_order, trend=t,
enforce_stationarity=False, enfore_invertibility=False)
model_fit = model.fit(disp=False)
yhat = model_fit.predict(len(data))
 
if i + 1 == test_len:
return yhat, model_fit
else:
return yhat
 
 def walk_forward_val(data, cfg):
"""
A walk forward validation technique used for time series data. Takes current value of x_test and predicts
value. x_test is then fed back into history for the next prediction.
"""
train, test = train_test_split(data)
pred = []
history = [i for i in train]
test_len = len(test)
 
for i in range(test_len):
if i + 1 == test_len:
yhat, s_model = sarima_model(history, cfg, test_len, i)
pred.append(yhat)
mse = mean_squared_error(test, pred)
return pred, mse, s_model
else:
yhat = sarima_model(history, cfg, test_len, i)
pred.append(yhat)
history.append(test[i])
pass
 
 if __name__ == '__main__':
start_time = time()
sarima_pred_plant2, sarima_mse, s_model = walk_forward_val(plant2_dcpower, configg)
time_len = time() - start_time
 
print(f'SARIMA runtime: {round(time_len/60,2)} mins')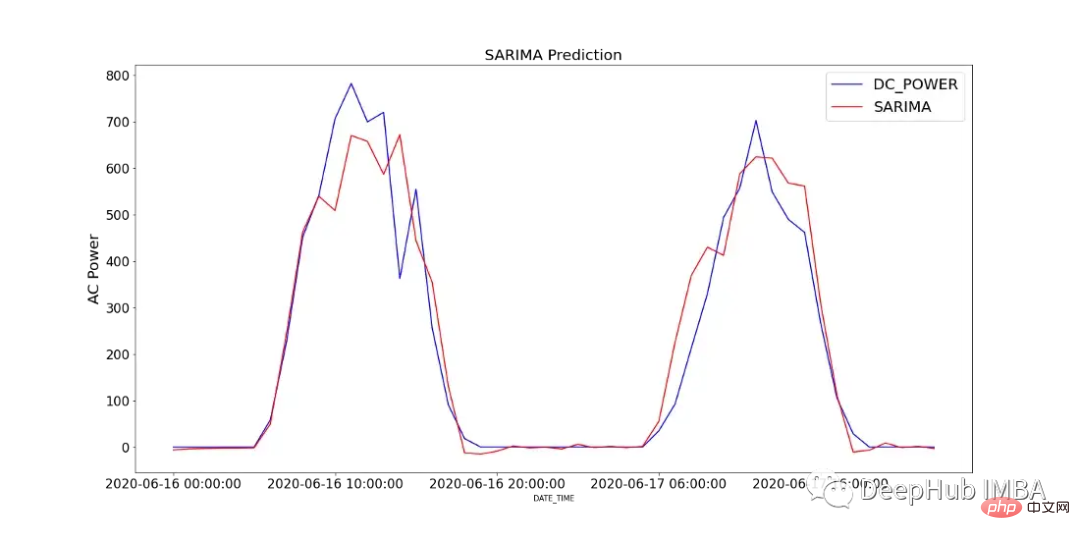

図 12 は、SARIMA モデルの予測値と、SP2 で 2 日間記録された DC 電力の比較を示しています。

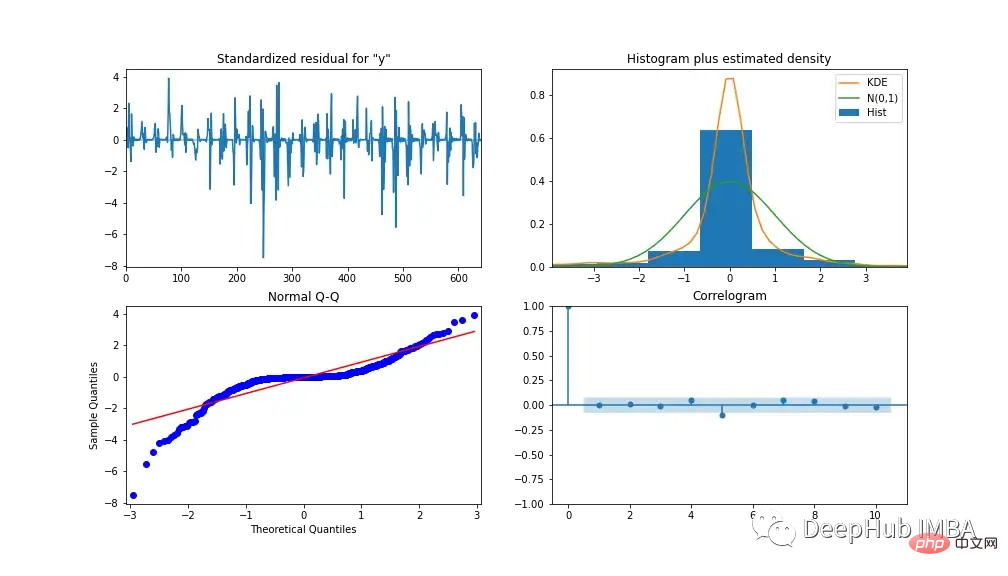
モデルのパフォーマンスを分析するために、図 13 にモデル診断を示します。相関プロットは、最初の遅れの後はほとんど相関を示さず、以下のヒストグラムは平均値 0 付近の正規分布を示しています。このことから、モデルはデータからそれ以上の情報を収集できないと言えます。

XGBoost

XGBoost (eXtreme Gradient Boosting) は、勾配ブースティング デシジョン ツリー アルゴリズムです。新しいデシジョン ツリー モデルを追加して既存のデシジョン ツリー スコアを変更するアンサンブル アプローチを使用します。 SARIMA とは異なり、XGBoost は多変量機械学習アルゴリズムです。つまり、モデルは複数の機能を採用してモデルのパフォーマンスを向上させることができます。

私たちは特徴エンジニアリングを使用してモデルの精度を向上させます。 3 つの追加特性も作成されました。これには、AC 電力と DC 電力の遅れバージョン、それぞれ S1_AC_POWER と S1_DC_POWER、および AC 電力を DC 電力で割った全体効率 EFF が含まれます。そして、データから AC_POWER と MODULE_TEMPERATURE を削除します。図 14 は、ゲイン (特徴を使用した分割の平均ゲイン) と重み (特徴がツリーに出現する回数) による特徴の重要度を示しています。

グリッド検索によるモデリングに使用されるハイパーパラメータを決定します。結果は次のようになります: *学習率 = 0.01、推定器の数 = 1200、サブサンプル = 0.8、ツリーによる列サンプル = 1 、レベル別の Colsample = 1、最小子の重み = 20、最大深度 = 10

MinMaxScaler を使用して、トレーニング データを 0 から 1 の間でスケーリングします (log-transform や などの他のスケーラーを試してみることもできます)。標準スケーラー、データの分布に依存します)。すべての独立変数を一定の時間だけ後方に移動することにより、データを教師あり学習データセットに変換します。

 import numpy as np
 import pandas as pd
 import xgboost as xgb
 from sklearn.preprocessing import MinMaxScaler
 from time import time
 
 def train_test_split(df, test_len=48):
"""
split data into training and testing.
"""
train, test = df[:-test_len], df[-test_len:]
return train, test
 
 def data_to_supervised(df, shift_by=1, target_var='DC_POWER'):
"""
Convert data into a supervised learning problem.
"""
target = df[target_var][shift_by:].values
dep = df.drop(target_var, axis=1).shift(-shift_by).dropna().values
data = np.column_stack((dep, target))
return data
 
 
 def xgb_forecast(train, x_test):
"""
XGBOOST model which outputs prediction and model.
"""
x_train, y_train = train[:,:-1], train[:,-1]
xgb_model = xgb.XGBRegressor(learning_rate=0.01, n_estimators=1500, subsample=0.8,
colsample_bytree=1, colsample_bylevel=1,
min_child_weight=20, max_depth=14, objective='reg:squarederror')
xgb_model.fit(x_train, y_train)
yhat = xgb_model.predict([x_test])
return yhat[0], xgb_model
 
 def walk_forward_validation(df):
"""
A walk forward validation approach by scaling the data and changing into a supervised learning problem.
"""
preds = []
train, test = train_test_split(df)
 
scaler = MinMaxScaler(feature_range=(0,1))
train_scaled = scaler.fit_transform(train)
test_scaled = scaler.transform(test)
 
train_scaled_df = pd.DataFrame(train_scaled, columns = train.columns, index=train.index)
test_scaled_df = pd.DataFrame(test_scaled, columns = test.columns, index=test.index)
 
train_scaled_sup, test_scaled_sup = data_to_supervised(train_scaled_df), data_to_supervised(test_scaled_df)
history = np.array([x for x in train_scaled_sup])
 
for i in range(len(test_scaled_sup)):
test_x, test_y = test_scaled_sup[i][:-1], test_scaled_sup[i][-1]
yhat, xgb_model = xgb_forecast(history, test_x)
preds.append(yhat)
np.append(history,[test_scaled_sup[i]], axis=0)
 
pred_array = test_scaled_df.drop("DC_POWER", axis=1).to_numpy()
pred_num = np.array([pred])
pred_array = np.concatenate((pred_array, pred_num.T), axis=1)
result = scaler.inverse_transform(pred_array)
 
return result, test, xgb_model
 
 if __name__ == '__main__':
start_time = time()
xgb_pred, actual, xgb_model = walk_forward_validation(dropped_df_cat)
time_len = time() - start_time
 
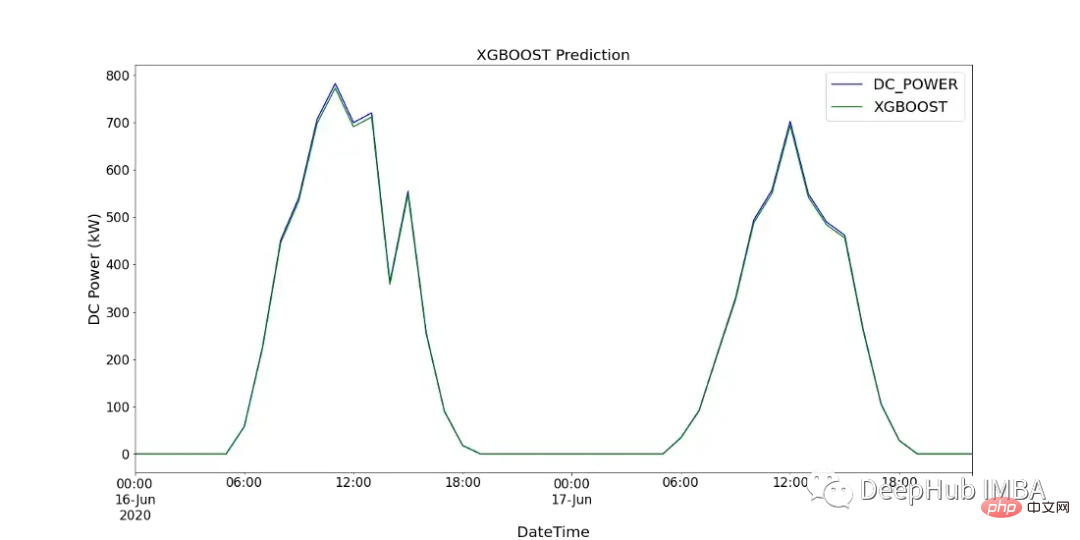
print(f'XGBOOST runtime: {round(time_len/60,2)} mins')

图15显示了XGBoost模型的预测值与SP2 2天内记录的直流功率的比较。

CNN-LSTM

CNN-LSTM (convolutional Neural Network Long - Short-Term Memory)是两种神经网络模型的混合模型。CNN是一种前馈神经网络，在图像处理和自然语言处理方面表现出了良好的性能。它还可以有效地应用于时间序列数据的预测。LSTM是一种序列到序列的神经网络模型，旨在解决长期存在的梯度爆炸/消失问题，使用内部存储系统，允许它在输入序列上积累状态。

在本例中，使用CNN-LSTM作为编码器-解码器体系结构。由于CNN不直接支持序列输入，所以我们通过1D CNN读取序列输入并自动学习重要特征。然后LSTM进行解码。与XGBoost模型类似，使用scikitlearn的MinMaxScaler使用相同的数据并进行缩放，但范围在-1到1之间。对于CNN-LSTM，需要将数据重新整理为所需的结构:[samples, subsequences, timesteps, features]，以便可以将其作为输入传递给模型。

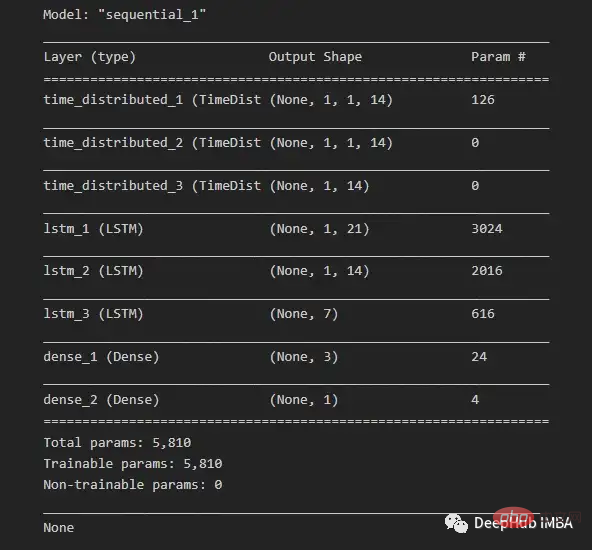
由于我们希望为每个子序列重用相同的CNN模型，因此使用timedidistributedwrapper对每个输入子序列应用一次整个模型。在下面的图16中可以看到最终模型中使用的不同层的模型摘要。

在将数据分解为训练数据和测试数据之后，将训练数据分解为训练数据和验证数据集。在所有训练数据(包括验证数据)的每次迭代之后，模型可以进一步使用这一点来评估模型的性能。

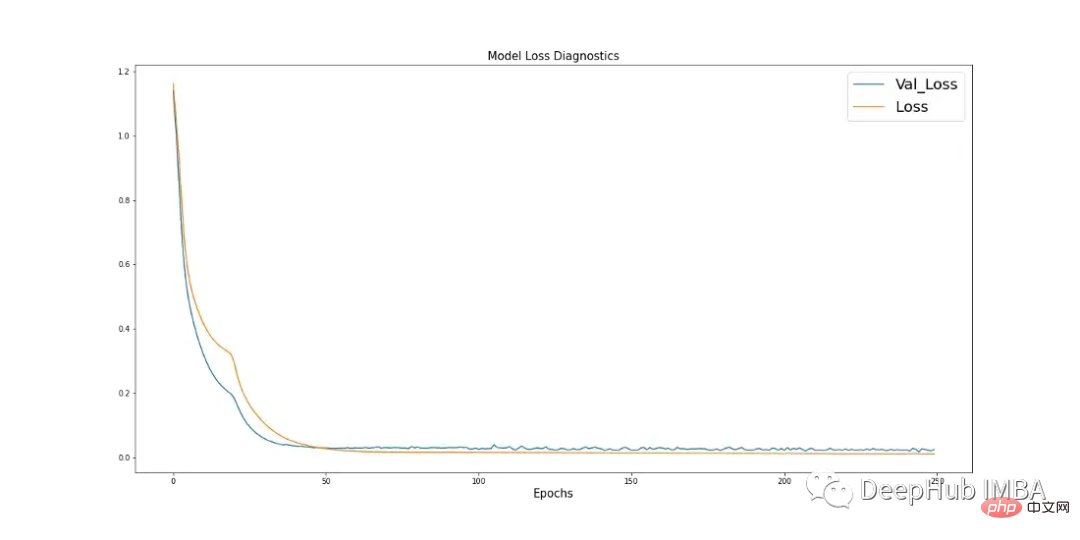
学习曲线是深度学习中使用的一个很好的诊断工具，它显示了模型在每个阶段之后的表现。下面的图17显示了模型如何从数据中学习，并显示了验证数据与训练数据的收敛。这是良好模特训练的标志。

import pandas as pd
 import numpy as np
 from sklearn.metrics import mean_squared_error
 from sklearn.preprocessing import MinMaxScaler
 import keras
 from keras.models import Sequential
 from keras.layers.convolutional import Conv1D, MaxPooling1D
 from keras.layers import LSTM, TimeDistributed, RepeatVector, Dense, Flatten
 from keras.optimizers import Adam
 
 n_steps = 1
 subseq = 1
 
 def train_test_split(df, test_len=48):
"""
Split data in training and testing. Use 48 hours as testing.
"""
train, test = df[:-test_len], df[-test_len:]
return train, test
 
 def split_data(sequences, n_steps):
"""
Preprocess data returning two arrays.
"""
x, y = [], []
for i in range(len(sequences)):
end_x = i + n_steps
 
if end_x > len(sequences):
break
x.append(sequences[i:end_x, :-1])
y.append(sequences[end_x-1, -1])
 
return np.array(x), np.array(y)
 
def CNN_LSTM(x, y, x_val, y_val):
"""
CNN-LSTM model.
"""
model = Sequential()
model.add(TimeDistributed(Conv1D(filters=14, kernel_size=1, activation="sigmoid",
input_shape=(None, x.shape[2], x.shape[3]))))
model.add(TimeDistributed(MaxPooling1D(pool_size=1)))
model.add(TimeDistributed(Flatten()))
model.add(LSTM(21, activation="tanh", return_sequences=True))
model.add(LSTM(14, activation="tanh", return_sequences=True))
model.add(LSTM(7, activation="tanh"))
model.add(Dense(3, activation="sigmoid"))
model.add(Dense(1))
 
model.compile(optimizer=Adam(learning_rate=0.001), loss="mse", metrics=['mse'])
history = model.fit(x, y, epochs=250, batch_size=36,
verbose=0, validation_data=(x_val, y_val))
 
return model, history
 
 # split and resahpe data
 train, test = train_test_split(dropped_df_cat)
 
 train_x = train.drop(columns="DC_POWER", axis=1).to_numpy()
 train_y = train["DC_POWER"].to_numpy().reshape(len(train), 1)
 
 test_x = test.drop(columns="DC_POWER", axis=1).to_numpy()
 test_y = test["DC_POWER"].to_numpy().reshape(len(test), 1)
 
 #scale data
 scaler_x = MinMaxScaler(feature_range=(-1,1))
 scaler_y = MinMaxScaler(feature_range=(-1,1))
 
 train_x = scaler_x.fit_transform(train_x)
 train_y = scaler_y.fit_transform(train_y)
 
 test_x = scaler_x.transform(test_x)
 test_y = scaler_y.transform(test_y)
 
 
 # shape data into CNN-LSTM format [samples, subsequences, timesteps, features] ORIGINAL
 train_data_np = np.hstack((train_x, train_y))
 x, y = split_data(train_data_np, n_steps)
 x_subseq = x.reshape(x.shape[0], subseq, x.shape[1], x.shape[2])
 
 # create validation set
 x_val, y_val = x_subseq[-24:], y[-24:]
 x_train, y_train = x_subseq[:-24], y[:-24]
 
 n_features = x.shape[2]
 actual = scaler_y.inverse_transform(test_y)
 
 # run CNN-LSTM model
 if __name__ == '__main__':
start_time = time()
 
model, history = CNN_LSTM(x_train, y_train, x_val, y_val)
prediction = []
 
for i in range(len(test_x)):
test_input = test_x[i].reshape(1, subseq, n_steps, n_features)
yhat = model.predict(test_input, verbose=0)
yhat_IT = scaler_y.inverse_transform(yhat)
prediction.append(yhat_IT[0][0])
 
time_len = time() - start_time
mse = mean_squared_error(actual.flatten(), prediction)
 
print(f'CNN-LSTM runtime: {round(time_len/60,2)} mins')
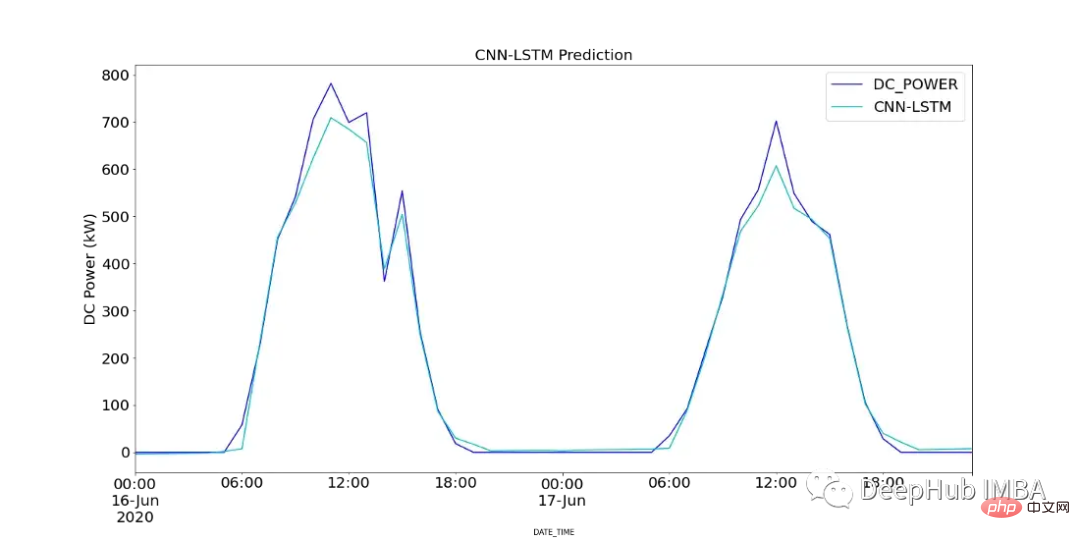
print(f"CNN-LSTM MSE: {round(mse,2)}")

图18显示了CNN-LSTM模型的预测值与SP2 2天内记录的直流功率的对比。

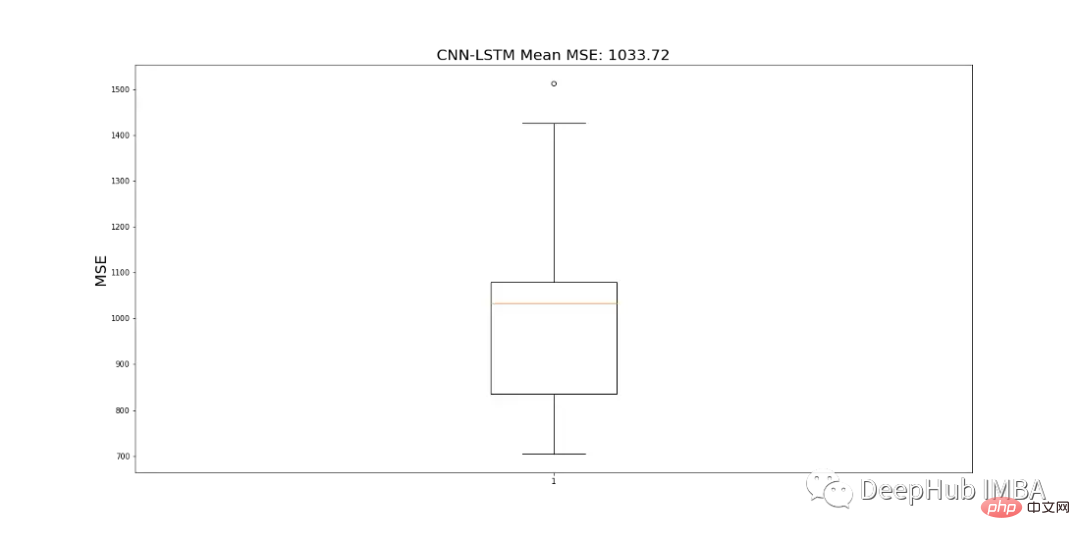
由于CNN-LSTM的随机性，该模型运行10次，并记录一个平均MSE值作为最终值，以判断模型的性能。图19显示了为所有模型运行记录的mse的范围。

结果对比

下表显示了每个模型的MSE (CNN-LSTM的平均MSE)和每个模型的运行时间(以分钟为单位)。

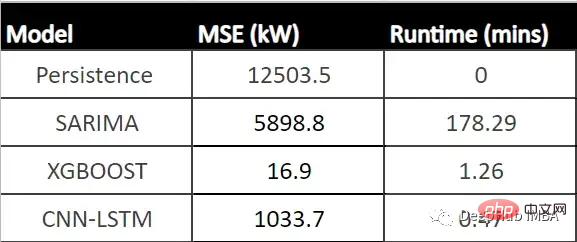
从表中可以看出，XGBoost的MSE最低、运行时第二快，并且与所有其他模型相比具有最佳性能。由于该模型显示了一个可以接受的每小时预测的运行时，它可以成为帮助运营经理决策过程的强大工具。

总结

在本文中我们分析了SP1和SP2，确定SP1性能较低。所以对SP2的进一步调查显示，并且查看了SP2中那些模块性能可能有问题，并使用假设检验来计算每个模块在统计上明显表现不佳的次数，' Quc1TzYxW2pYoWX '模块显示了约850次低性能计数。

我们使用数据训练三个模型：SARIMA、XGBoost和CNN-LSTM。SARIMA表现最差，XGBOOST表现最好，MSE为16.9，运行时间为1.43 min。所以可以说XGBoost在表格数据中还是最优先得选择。

以上がSARIMA、XGBoost、CNN-LSTM に基づく時系列予測方法を比較します。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。