ホームページ >Java >&#&チュートリアル >Java アルゴリズムの設計と分析: 分割統治アルゴリズムの例の詳細な説明
Java アルゴリズムの設計と分析: 分割統治アルゴリズムの例の詳細な説明
- 王林転載
- 2023-04-23 11:22:07843ブラウズ
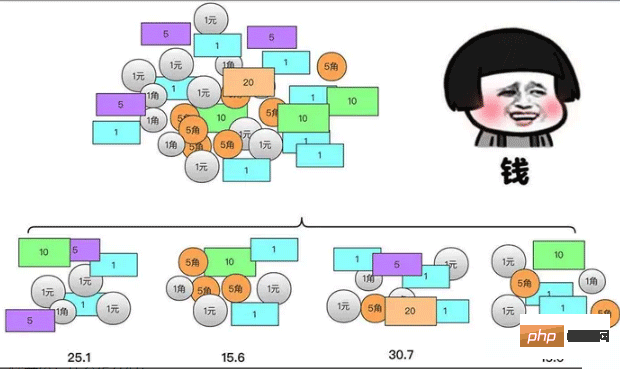
- それぞれの小さなお金の山を計算する方法は、最も大きなお金の山を計算する方法と同じです (違いは次のとおりです)サイズ)
- 次に、大きなお金の山の合計は、実際には小さなお金の山の結果の合計です。このように、実際には分割統治の考え方が存在します。
分割統治アルゴリズムの説明は、文字通りに理解するのが簡単です。分割統治には実際にはマージ プロセスが含まれます:
分割: より小さな問題を再帰的に解決します (終端層に到達するか、解決できるときに停止します)
征服: 再帰的に解決するか、解決します問題が十分に小さい場合は直接。
結合: サブ問題の解決策を親クラスの問題に構築します
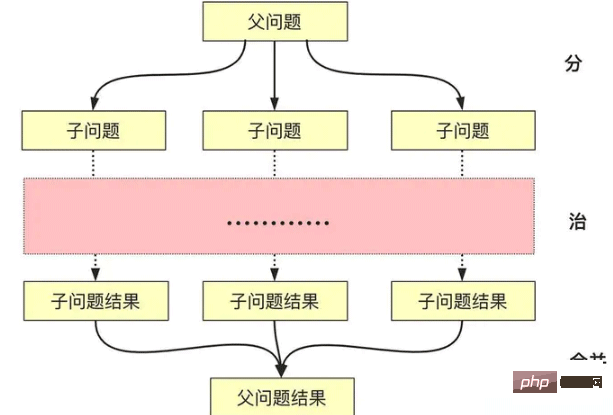
## 1. 元の問題の規模は通常比較的大きく、直接解決することは困難ですが、問題をある程度まで縮小すると、より簡単に解決できるようになります。
- 2. 問題は、同じ (同様の) 解決方法を使用して、多数の小さなサブ問題に分解できます。そして、副次的な問題に対する解決策は独立しており、互いに影響しません。
- 3. 問題の解決策は、問題に分解された部分問題をマージすることで得られます。
- 分割統治アルゴリズムと再帰の間にはどのような関係があるのか疑問に思われるかもしれません。実際、分割統治は重要な考え方であり、問題を分割し、征服し、統合するプロセスに焦点を当てています。再帰は、メソッドを使用して自分自身を呼び出して前後のプロセスを形成する方法 (ツール) であり、分割統治はそのような複数の往復プロセスを利用する場合があります。
- 2. サブ問題は完全に独立しているわけではありません。一部の区間問題または区間間問題では、分割統治の結果が区間をまたいで発生する場合があります。そこから学ぶ必要があります。問題を考えるときは慎重に。
- 3.1. 二分探索
#シーケンス順序
結果は値です
-
通常の二等分では、完全な区間が 2 つの区間に分割され、その 2 つの区間は次のようになります。値を個別に計算して結果を確認しますが、順序付けされた間隔を通じて結果がどの間隔にあるかを直接判断できるため、2 つの間隔のうちの 1 つだけを計算し、最後まで続行する必要があります。再帰的実装方法と非再帰的実装方法がありますが、非再帰的実装方法の方が一般的に使用されます:
public int searchInsert(int[] nums, int target) { if(nums[0]>=target)return 0;//剪枝 if(nums[nums.length-1]==target)return nums.length-1;//剪枝 if(nums[nums.length-1]<target)return nums.length; int left=0,right=nums.length-1; while (left<right) { int mid=(left+right)/2; if(nums[mid]==target) return mid; else if (nums[mid]>target) { right=mid; } else { left=mid+1; } } return left; }3.2. クイック ソート
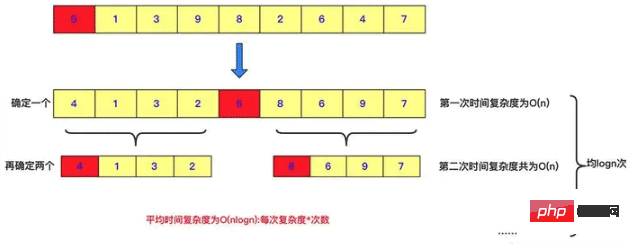
クイック ソートも分割統治の一例であり、クイック ソートの各パスで番号が選択され、この番号より小さい番号が左側に配置され、その番号が右側のこの数値よりも大きいです。その後、再帰的に除算と征服を行って 2 つの部分区間を解決します。もちろん、クイック ソートは除算時に多くの作業を行います。すべての部分が一番下にある場合、このシーケンスの値はソートされた値です。これは分割統治の現れです。

public void quicksort(int [] a,int left,int right) { int low=left; int high=right; //下面两句的顺序一定不能混,否则会产生数组越界!!!very important!!! if(low>high)//作为判断是否截止条件 return; int k=a[low];//额外空间k,取最左侧的一个作为衡量,最后要求左侧都比它小,右侧都比它大。 while(low<high)//这一轮要求把左侧小于a[low],右侧大于a[low]。 { while(low<high&&a[high]>=k)//右侧找到第一个小于k的停止 { high--; } //这样就找到第一个比它小的了 a[low]=a[high];//放到low位置 while(low<high&&a[low]<=k)//在low往右找到第一个大于k的,放到右侧a[high]位置 { low++; } a[high]=a[low]; } a[low]=k;//赋值然后左右递归分治求之 quicksort(a, left, low-1); quicksort(a, low+1, right); }3.3. マージソート (逆順)
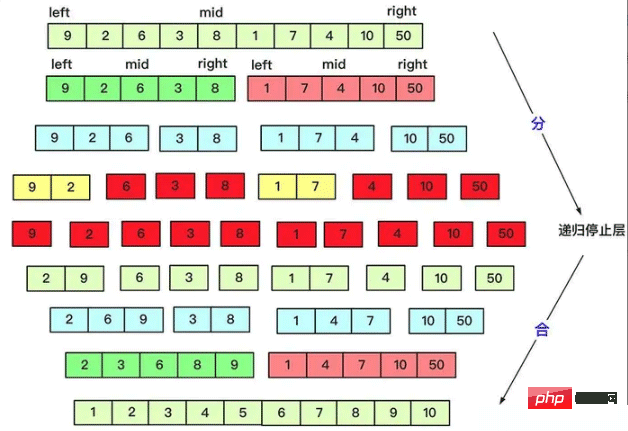
クイックソートは分割時に多くの作業を行いますが、マージはその逆です。必要な結果は 2 つの順序付けされたシーケンスの O(n) レベルの複雑さで取得できるため、マージの際にはすでに順序どおりにマージされています。マージソートに基づく逆順序数の変形も、分割統治のアイデアによって解決されます。

private static void mergesort(int[] array, int left, int right) { int mid=(left+right)/2; if(left<right) { mergesort(array, left, mid); mergesort(array, mid+1, right); merge(array, left,mid, right); } } private static void merge(int[] array, int l, int mid, int r) { int lindex=l;int rindex=mid+1; int team[]=new int[r-l+1]; int teamindex=0; while (lindex<=mid&&rindex<=r) {//先左右比较合并 if(array[lindex]<=array[rindex]) { team[teamindex++]=array[lindex++]; } else { team[teamindex++]=array[rindex++]; } } while(lindex<=mid)//当一个越界后剩余按序列添加即可 { team[teamindex++]=array[lindex++]; } while(rindex<=r) { team[teamindex++]=array[rindex++]; } for(int i=0;i<teamindex;i++) { array[l+i]=team[i]; } }3.4. 動的計画法を使用して、最大部分列と
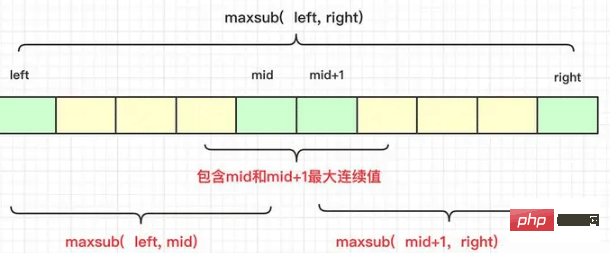
部分列の最大合計の問題を解決できますが、除算も使用できます。 and-conquer アルゴリズム 問題を解決しますが、サブシーケンスの合計には長さの問題が含まれるため、最大のサブシーケンスの合計はマージ時に単純なマージではありません。そのため、正しい結果がすべて左端または右端にあるとは限りませんが、次の結果が表示される場合があります:
- #中心の完全に左 #中心の完全に右
- 中央に左右のノードを含むシーケンス
最大サブシーケンス合計のコードは次のとおりです: したがって、具体的に考えると、再帰的に求めることのできない真ん中の最大値列の結果を計算して、左右の比較に参加させる必要がある。
したがって、具体的に考えると、再帰的に求めることのできない真ん中の最大値列の結果を計算して、左右の比較に参加させる必要がある。 public int maxSubArray(int[] nums) { int max=maxsub(nums,0,nums.length-1); return max; } int maxsub(int nums[],int left,int right) { if(left==right) return nums[left]; int mid=(left+right)/2; int leftmax=maxsub(nums,left,mid);//左侧最大 int rightmax=maxsub(nums,mid+1,right);//右侧最大 int midleft=nums[mid];//中间往左 int midright=nums[mid+1];//中间往右 int team=0; for(int i=mid;i>=left;i--) { team+=nums[i]; if(team>midleft) midleft=team; } team=0; for(int i=mid+1;i<=right;i++) { team+=nums[i]; if(team>midright) midright=team; } int max=midleft+midright;//中间的最大值 if(max<leftmax) max=leftmax; if(max<rightmax) max=rightmax; return max; }3.5. 最近点ペア最近点ペアは分割統治に非常に成功しています。メソッド アプリケーションの 1 つ。 2 次元の座標軸上にはいくつかの点の座標があり、最も近い 2 点間の距離を求めることができます。直接求めると、列挙の暴力は非常に膨大な計算量になります。通常、分割統治法による最適化 この種の問題。
 これを直接 2 つの部分に分割し、分割統治を計算すると、最も短いものが左側にあり、もう 1 つが右側にある場合、必ずわかります。問題が発生するでしょう。それを最適化することができます。
これを直接 2 つの部分に分割し、分割統治を計算すると、最も短いものが左側にあり、もう 1 つが右側にある場合、必ずわかります。問題が発生するでしょう。それを最適化することができます。 具体的な最適化計画に関しては、x または y 次元を考慮し、データを 2 つの領域に分割し、最初に左側と右側の領域でそれぞれ最短の点のペアを (同じ方法に従って) 計算します。次に、2 つの間の短い距離に従って左右にカバーし、カバーされた左右の点の間の距離を計算し、最小距離を見つけて、現在の最短距離と比較します。
 このようにして、この 1 回限りの操作 (サブケースに関係なく) では、左側の赤い点がほとんどの場合の距離計算を回避していることがわかります。右側の赤い点 (O (n2 の時間計算量))。実際、左右の間隔で内部計算を実行するとき、実際には多くの分割統治計算が再帰的に実行されます。図に示すように:
このようにして、この 1 回限りの操作 (サブケースに関係なく) では、左側の赤い点がほとんどの場合の距離計算を回避していることがわかります。右側の赤い点 (O (n2 の時間計算量))。実際、左右の間隔で内部計算を実行するとき、実際には多くの分割統治計算が再帰的に実行されます。図に示すように:  # これにより、多くの計算を節約できます。
# これにより、多くの計算を節約できます。 しかし、この種の分割統治には問題があり、2 次元座標では特定の方法と特定の軸に点が集まっているため、効果が明確ではない可能性があります (点はすべて存在します)。 x=2 付近では x の除算には影響しません)、大きい)、注意が必要です。
ac のコードは次のとおりです:import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.io.OutputStreamWriter; import java.io.PrintWriter; import java.io.StreamTokenizer; import java.util.ArrayList; import java.util.Arrays; import java.util.Comparator; import java.util.List; public class Main { static int n; public static void main(String[] args) throws IOException { StreamTokenizer in=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in))); PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out)); //List<node>list=new ArrayList(); while(in.nextToken()!=StreamTokenizer.TT_EOF) { n=(int)in.nval;if(n==0) {break;} node no[]=new node[n]; for(int i=0;i<n;i++) { in.nextToken();double x=in.nval; in.nextToken();double y=in.nval; // list.add(new node(x,y)); no[i]=new node(x,y); } Arrays.sort(no, com); double min= search(no,0,n-1); out.println(String.format("%.2f", Math.sqrt(min)/2));out.flush(); } } private static double search(node[] no, int left,int right) { int mid=(right+left)/2; double minleng=0; if(left==right) {return Double.MAX_VALUE;} else if(left+1==right) {minleng= (no[left].x-no[right].x)*(no[left].x-no[right].x)+(no[left].y-no[right].y)*(no[left].y-no[right].y);} else minleng= min(search(no,left,mid),search(no,mid,right)); int ll=mid;int rr=mid+1; while(no[mid].y-no[ll].y<=Math.sqrt(minleng)/2&&ll-1>=left) {ll--;} while(no[rr].y-no[mid].y<=Math.sqrt(minleng)/2&&rr+1<=right) {rr++;} for(int i=ll;i<rr;i++) { for(int j=i+1;j<rr+1;j++) { double team=0; if(Math.abs((no[i].x-no[j].x)*(no[i].x-no[j].x))>minleng) {continue;} else { team=(no[i].x-no[j].x)*(no[i].x-no[j].x)+(no[i].y-no[j].y)*(no[i].y-no[j].y); if(team<minleng)minleng=team; } } } return minleng; } private static double min(double a, double b) { // TODO 自动生成的方法存根 return a<b?a:b; } static Comparator<node>com=new Comparator<node>() { @Override public int compare(node a1, node a2) { // TODO 自动生成的方法存根 return a1.y-a2.y>0?1:-1; }}; static class node { double x; double y; public node(double x,double y) { this.x=x; this.y=y; } } }
以上がJava アルゴリズムの設計と分析: 分割統治アルゴリズムの例の詳細な説明の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。


 したがって、具体的に考えると、再帰的に求めることのできない真ん中の最大値列の結果を計算して、左右の比較に参加させる必要がある。
したがって、具体的に考えると、再帰的に求めることのできない真ん中の最大値列の結果を計算して、左右の比較に参加させる必要がある。 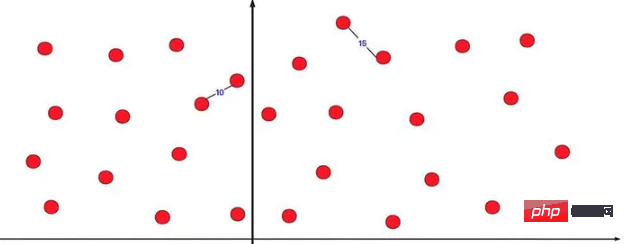 これを直接 2 つの部分に分割し、分割統治を計算すると、最も短いものが左側にあり、もう 1 つが右側にある場合、必ずわかります。問題が発生するでしょう。それを最適化することができます。
これを直接 2 つの部分に分割し、分割統治を計算すると、最も短いものが左側にあり、もう 1 つが右側にある場合、必ずわかります。問題が発生するでしょう。それを最適化することができます。 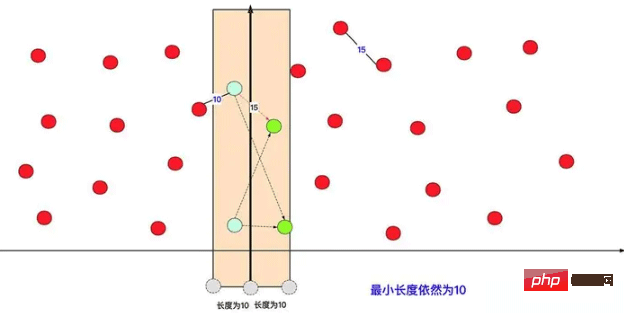 このようにして、この 1 回限りの操作 (サブケースに関係なく) では、左側の赤い点がほとんどの場合の距離計算を回避していることがわかります。右側の赤い点 (O (n2 の時間計算量))。実際、左右の間隔で内部計算を実行するとき、実際には多くの分割統治計算が再帰的に実行されます。図に示すように:
このようにして、この 1 回限りの操作 (サブケースに関係なく) では、左側の赤い点がほとんどの場合の距離計算を回避していることがわかります。右側の赤い点 (O (n2 の時間計算量))。実際、左右の間隔で内部計算を実行するとき、実際には多くの分割統治計算が再帰的に実行されます。図に示すように: 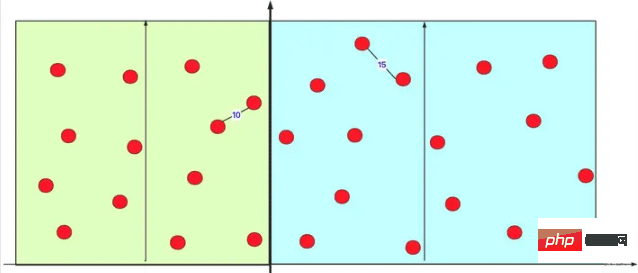 # これにより、多くの計算を節約できます。
# これにより、多くの計算を節約できます。