ホームページ >Java >&#&チュートリアル >Java でヒープを使用して Top-k 問題を解決するにはどうすればよいですか?
Java でヒープを使用して Top-k 問題を解決するにはどうすればよいですか?
- 王林転載
- 2023-04-21 10:19:161094ブラウズ
1. ヒープとは何ですか?
ヒープの構造
ヒープは実際にはバイナリツリーの一種ですが、通常のバイナリツリーはチェーン構造でデータを格納しますが、ヒープはデータを配列に順番に格納します。それでは、どのようなバイナリツリーが逐次保存に適しているのでしょうか?
通常のバイナリ ツリーが配列に格納できると仮定すると、次の構造が得られます。
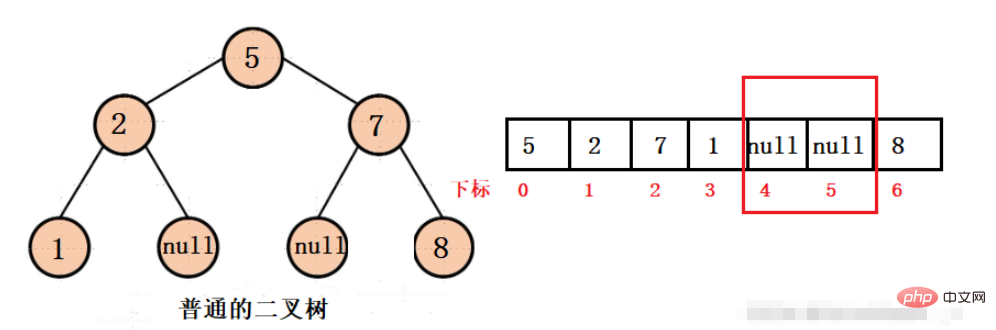
次の構造があることがわかります。バイナリ ツリー値の中央にスペースがある場合、配列の記憶スペースが無駄になりますが、どのような状況でスペースが無駄にならないでしょうか?それは完全な二分木です。
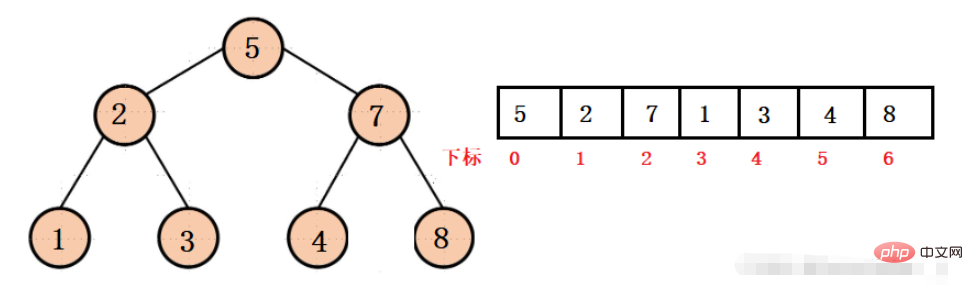
上記の構造から、チェーン構造のポインタを使用して子ノードまたは親ノードにアクセスすることはできません。対応する添え字を介してのみアクセスできます。実際には比較的単純です。
たとえば、以下の図では:
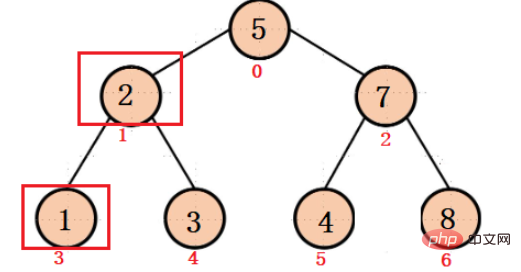
ノード 2 の添字は 1 であることがわかっており、
その左側の子の添字は 2 * 2 となります。 1 = 3
彼の右の子の添字は次のとおりです: 2 * 2 2 = 4
逆に、ノード 1 の添字は 3、ノード 3 の添字は 3 であることがわかります。が 4 の場合、
ノード 1 の親ノード インデックスは次のとおりです: (3 - 1) / 2 = 1
ノード 3 の親ノード インデックスは次のとおりです: (4 - 1) / 2 = 1
大きなルート ヒープ VS 小さなルート ヒープ
大きなルート ヒープ (最大ヒープ)
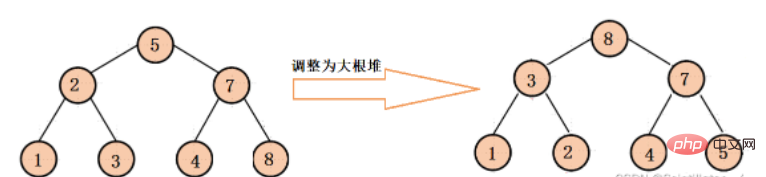
大きなルート ヒープは、各バイナリ ツリーのルート ノードは左右の子ノードより大きいです
最後のサブツリーのルート ノードから各サブツリーのルート ノードまで調整を開始し、各サブツリーが大きなルートになるように下方に調整します。ヒープを変更し、最後にバイナリ ツリー全体が大きなルート ヒープになるように下方調整を行います (この調整は主に後のヒープ ソートのためのものです)。
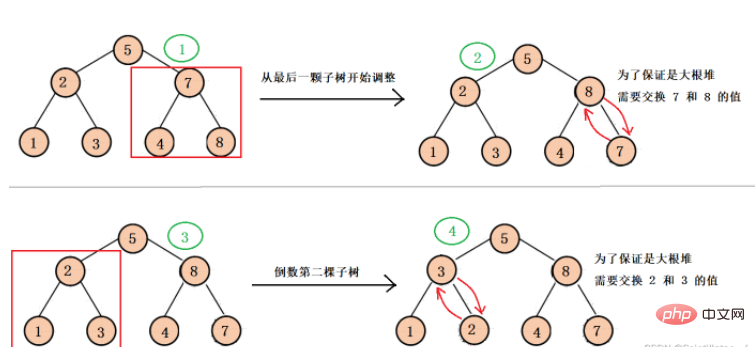
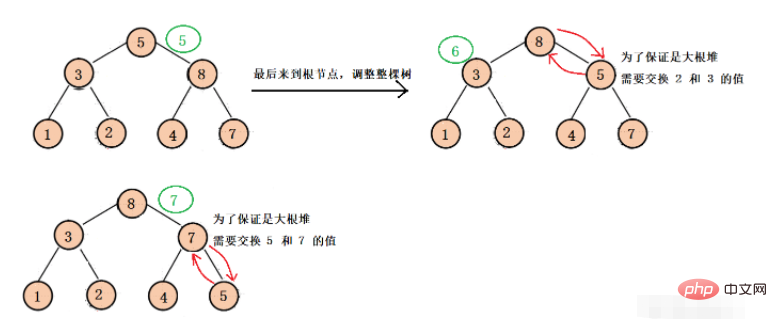 #実装方法コード付きですか?
#実装方法コード付きですか?
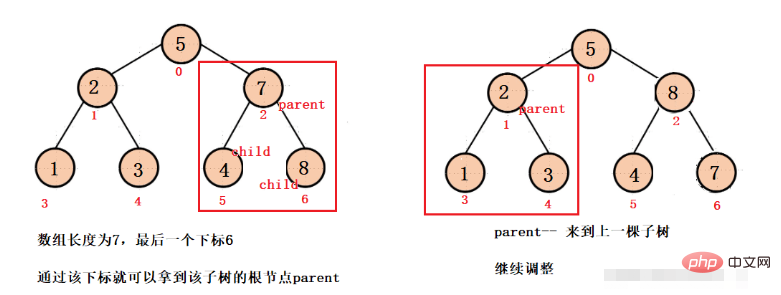
最初に最後のサブツリーから調整し、次に最後のサブツリーのルート ノードの親を取得する必要があります。配列の最後のノードの添字が len - 1 であり、このノードが最後のサブツリーであることがわかっています。ツリーの左または右の子の場合、子の添え字に基づいてルート ノードの添え字 (親) を取得できます。親 -- ルート ノードに到達するまで各サブツリーを調整し、最後のノードに到達するまで下方に調整できます。大きな根山が得られます。
// 将数组变成大根堆结构
public void createHeap(int[] arr){
for (int i = 0; i < arr.length; i++) {
elem[i] = arr[i];// 放入elem[],假设不需要扩容
usedSize++;
}
// 得到根节点parent, parent--依次来到每颗子树的根节点,
for (int parent = (usedSize-1-1)/2; parent >= 0; parent--) {
// 依次向下搜索,使得每颗子树都变成大根堆
shiftDown(parent,usedSize);
}
}
// 向下搜索变成大根堆
public void shiftDown(int parent,int len){
int child = parent*2+1;// 拿到左孩子
while (child < len){
// 如果有右孩子,比较左右孩子大小,得到较大的值和父节点比较
if (child+1 < len && (elem[child] < elem[child+1])){
child++;
}
// 比较较大的孩子和父节点,看是否要交换
int max = elem[parent] >= elem[child] ? parent : child;
if (max == parent) break;// 如果不需要调整了,说明当前子树已经是大根堆了,直接 break
swap(elem,parent,child);
parent = child;// 继续向下检测,看是否要调整
child = parent*2+1;
}
}
public void swap(int[] arr,int i,int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
} 小さなルート ヒープ (最小ヒープ)
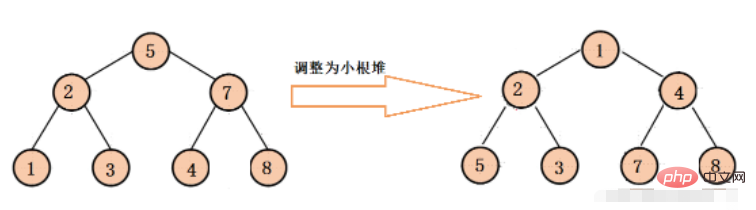
小さなルート ヒープ (最小ヒープ)
小さなルート ヒープにより、各バイナリ ツリーのルート ノードが左右の子ノードよりも小さくなります。ノード
調整プロセスは上記と同じです。
 プライオリティ キュー (PriorityQueue)
プライオリティ キュー (PriorityQueue)
Java では、プライオリティ キューとも呼ばれるヒープ データ構造 (PriorityQueue) が提供されます。オブジェクトの場合、データが追加されていない小さなルート ヒープが得られます。それに要素を追加または削除できます。要素が削除または追加されるたびに、システムは全体的な調整を行い、再び小さなルート ヒープに調整します。 .山盛り。
// 默认得到一个小根堆
PriorityQueue<Integer> smallHeap = new PriorityQueue<>();
smallHeap.offer(23);
smallHeap.offer(2);
smallHeap.offer(11);
System.out.println(smallHeap.poll());// 弹出2,剩余最小的元素就是11,会被调整到堆顶,下一次弹出
System.out.println(smallHeap.poll());// 弹出11
// 如果需要得到大根堆,在里面传一个比较器
PriorityQueue<Integer> BigHeap = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});2. 上位 k 個の問題を解決するためのアイデア
例: 多数の要素があり、最初の 3 つの最小要素を見つけるように求められます。
アイデア 1: 配列を小さいものから大きいものに並べ替え、配列の最初の 3 つの要素を取得します。ただし、この方法は時間がかかりすぎるため、お勧めできません。
アイデア 2: すべての要素をヒープ構造に配置し、次に 3 つの要素をポップアップします。各ポップアップ要素は現在のヒープ内で最小であり、3 つのポップアップ要素は最初の 3 つの最小要素になります。要素。
このアイデアは実現可能ですが、要素が 1,000,000 個あり、最初の 3 つの最小要素のみをポップアップすると仮定すると、サイズ 1,000,000 のヒープが使用されます。これを実行するとスペースの複雑さが高すぎるため、この方法はお勧めできません。
3 つのアイデア:
3 つの最小の要素を取得し、サイズ 3 のヒープを構築する必要があります。現在のヒープ構造がちょうど 3 つの要素で満たされていると仮定すると、これは3 つの要素は、現在の最小の 3 つの要素です。 4 番目の要素が必要な要素の 1 つであると仮定すると、最初の 3 つの要素のうち少なくとも 1 つは必要なものではないため、それをポップする必要があります。
取得したいのは最初の 3 つの最小要素であるため、現在のヒープ構造の最大の要素が必要なものであってはなりません。そこで、ここでは大きなルート ヒープを構築します。要素をポップし、配列全体が走査されるまで 4 番目の要素を挿入します。
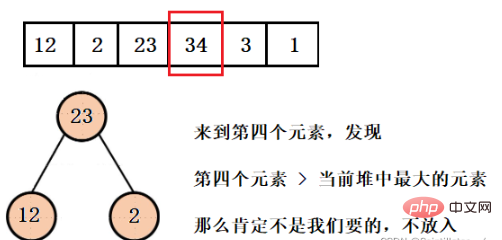
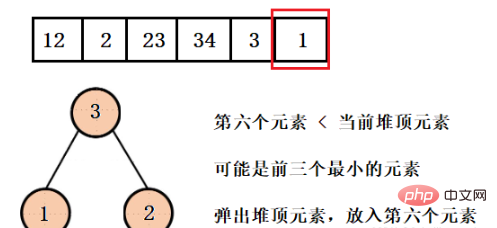
这样我们就得到了只含有前三个最小元素的堆,并且可以看到堆的大小一直都是3,而不是有多少数据就建多大的堆,然后再依次弹出元素就行了。
// 找前 k个最小的元素
public static int[] topK(int[] arr,int k){
// 创建一个大小为 k的大根堆
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k,new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});
for (int i = 0; i < arr.length; i++) {
if (i < k){
// 放入前 k 个元素
maxHeap.offer(arr[i]);
}else{
// 从第 k+1个元素开始进行判断是否要入堆
if (maxHeap.peek() > arr[i]){
maxHeap.poll();
maxHeap.offer(arr[i]);
}
}
}
int[] ret = new int[k];
for (int i = 0; i < k; i++) {
ret[i] = maxHeap.poll();
}
return ret;
}以上がJava でヒープを使用して Top-k 問題を解決するにはどうすればよいですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

