再帰的アルゴリズムをより深く理解するにはどうすればよいでしょうか? Pythonのサンプルを詳しく解説

再帰は確かに比較的抽象的な数学的論理であり、「プログラムが独自のアルゴリズムを呼び出す」と単純に理解できます。

Wikipedia の再帰の説明は次のとおりです:

再帰 (英語: Recursion) は、数学やコンピュータ サイエンスにおいて、再帰とも訳され、関数メソッドの定義で関数自体を使用することを指します。再帰という用語は、自己相似的な方法で物事を繰り返すプロセスを説明するためによく使用されます。

たとえば、2 つのミラーが互いにほぼ平行である場合、ミラー内にネストされたイメージは無限再帰の形で表示されます。それは自己複製のプロセスとしても理解できます。

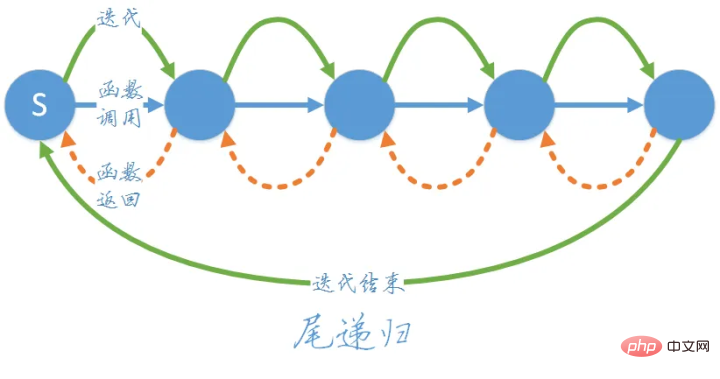
「Pass」は渡すこと、「Return」は返すことを意味し、まずレイヤーごとにメソッドを渡し、次に最後のレイヤーに渡して結果を返します。

たとえば、核酸検査の列に並んだとき、私の前に 100 人がいたので、医療従事者の退勤時間を聞きたかったのです。と、目の前にいるお兄さんに聞いたら、また聞いてきて、前の人が一人ずつ渡して、最後に医療スタッフに渡して、医療スタッフは午後6時に仕事を終えると答えました。この言葉は折り返して私に届き、医療従事者は6時に退勤したことを知りました。

このプロセスは再帰的なプロセスであり、「メッセージを渡す」こと自体がメソッドだとすると、メッセージを送信するプロセス全体が独自のメソッドを呼び出し、最終的に結果を取得することになります。

これはサイクルとは異なります。サイクルとは、全員にヘッドフォンを装着するのと同じであり、その後、「仲介者」が医療スタッフの退勤時間を知っているかどうかを一人ずつ尋ねます。医療スタッフに尋ねると、答えが得られ、「エージェント」は私に6時に仕事を終えるように言いました。

本質的に、再帰とは、玉ねぎの皮をむくように、大きな問題を継続的に分解し、最終的に最小レベルまで分解して、解の結果を返すことです。

Python を使用して再帰関数の最も単純な例を示し、再帰アプリケーションとは何かについて説明します。

階乗を求める関数など、ループ演算を実装するために関数自体を呼び出しているのをよく見かけます。

整数 n の階乗は、n*(n-1)*(n-2)*...*3*2*1 です。

次の 5 行の Python コードで階乗の計算を実現できます。

def fact(n):
''' n表示要求的数的阶乘 '''
if n==1:
return n 
n = n*fact(n-1)
return n
print(factorial(5))

多くの人は、ここでの計算ロジック、なぜファクト関数が自分自身を呼び出して最終的に結果を取得するのかについて混乱しているかもしれません。

数学的論理に従って推論できます:

整数 n の階乗は次のようになります: fat(n) = n*(n-1)*...*3*2*1 。

整数 n-1 の階乗は、fact(n-1) = (n-1)*(n-2)*...*3*2*1 となります。

したがって、fact(n) = n*fact(n-1) と推論できます。

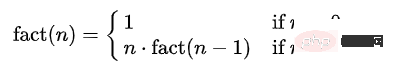
数値ごとに呼び出せるファクト メソッドはありますか? 最後に n=1 が呼び出されるとき、結果 n の階乗が返されます。

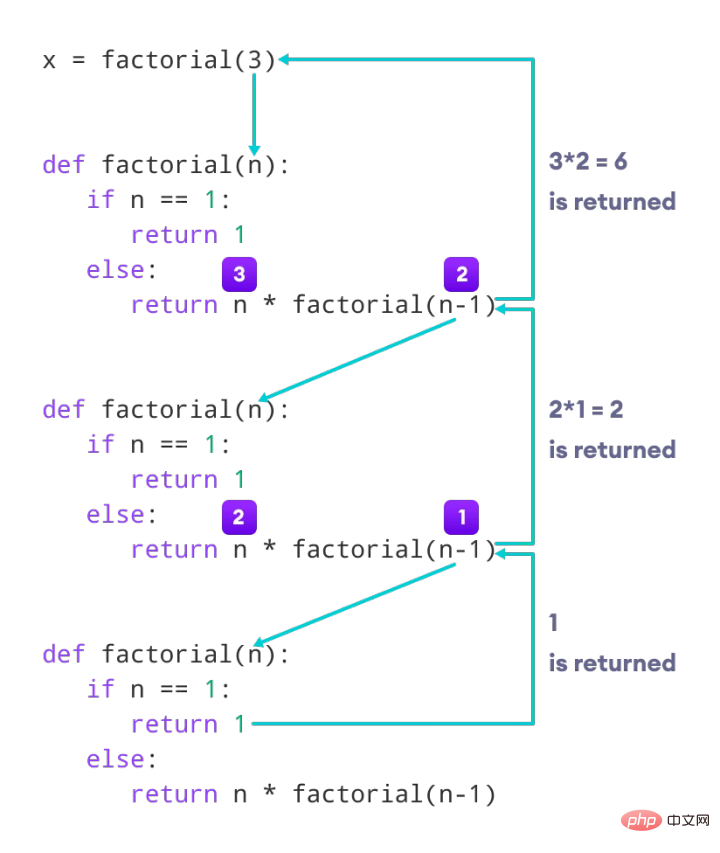
上の図を見てください。再帰関数は層ごとに呼び出され、最終的に n=1 のときに結果が上向きに返されます。

これは再帰のプロセス全体です。再帰を正確に定義すると、次の 3 つの点に要約できます:

1. 少なくとも 1 つの明確な終了条件があります。再帰。

2. 再帰が終了したら解を与えます。

3. 再帰のより深いレベルに入るたびに、問題のサイズ (計算量) は最後の再帰と比較して減少するはずです。

上記のコードを例として挙げます。

def factorial(n):
''' n表示要求的数的阶乘 '''
if n==1: # 1、明确递归终止条件；
return n # 2、递归终止时的处理办法
n = n*factorial(n-1) # 递去
return n# 归来

一般的な階乗の場合に加えて、再帰の古典的な使用法であるフィボナッチ数列もあります。

フィボナッチ数列: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89...

この数列は 3 番目の項目から始まり、各項は前の 2 つの項の合計に等しい。

次のように再帰的に定義されます: F(0)=0, F(1)=1, F(n)=F(n - 1) F(n - 2)(n ≥ 2, n ∈ N*)。

Python では、再帰関数を使用してフィボナッチ数列を実装できます:

# 1，1，2，3，5，8，13，21，34，55，试判断数列第12个数是哪个？
def fab(n):
''' n为斐波那契数列 '''
if n <= 2:
v = 1
return v 
v = fab(n-1)+fab(n-2) 
return v

print(fab(12)) 

数学的手法を使用して導出します:

• fab(0 ) = 0 (初期値)価値）。
• fab(1) = 1(初期値)。
• 1 より大きいすべての整数 n の場合: fab(n) = fab(n-1) fab(n-2) (再帰的定義)。

実は、上記の 2 つの再帰的な場合は、高校数学の知識である数学的帰納法で説明できます。

一般に、自然数 n に関連する命題 P(n) を証明するには、次の手順があります:

(1) n が最初の値を取るときに命題が真であることを証明します。 n0。一般的なシーケンスでは、n0 は値 0 または 1 をとりますが、特殊な場合もあります。

(2) n=k (k≧n0、kは自然数)のときに命題が真であると仮定し、n=k 1のときにも命題が真であることを証明します。

(1) (2) に基づいて、すべての自然数 n (≥n0) に対して、命題 P(n) は真です。

数学的な説明に加えて、私は以前に誰かが再帰についてより鮮やかな説明をしているのを見たことがあります。

1、我们已经完成了吗?如果完成了，返回结果。如果没有这样的终止条件，递归将会永远地继续下去。

2、如果没有，则简化问题，解决较容易的问题，并将结果组装成原始问题的解决办法。然后返回该解决办法。

哈哈,到这里大家是不是对递归有了一个更加深刻的认识。

如果还不清楚，没关系，这里还有更多的递归案例，用Python来实现，可以说非常简洁。

「最大公因数：」

def gcd(m, n):
if n == 0:
return m
else:
return gcd(n, m%n)

「从 1 到 n 的数字之和：」

def sumnums(n):
if n == 1:
return 1
return n + sumnums(n - 1)

print(sumnums(3))

「字符串倒序：」

def reverse(string):
if len(string) == 0:
return string
else:
return reverse(string[1:]) + string[0]

reverseme = '我是帅哥'
print(reverse(reverseme))

「汉诺塔问题：」

def towerOfHanoi(numrings, from_pole, to_pole, aux_pole):
if numrings == 1:
print('Move ring 1 from', from_pole, 'pole to', to_pole, 'pole')
return
towerOfHanoi(numrings - 1, from_pole, aux_pole, to_pole)
print('Move ring', numrings, 'from', from_pole, 'pole to', to_pole, 'pole')
towerOfHanoi(numrings - 1, aux_pole, to_pole, from_pole)
numrings = 2
towerOfHanoi(numrings, 'Left', 'Right', 'Middle')

「二分法找有序列表指定值：」

data = [1,3,6,13,56,123,345,1024,3223,6688]
def dichotomy(min,max,d,n):
'''
min表示有序列表头部索引
max表示有序列表尾部索引
d表示有序列表
n表示需要寻找的元素
'''
mid = (min+max)//2
if mid==0:
return 'None'
elif d[mid]<n:
print('向右侧找！')
return dichotomy(mid,max,d,n)
elif d[mid]>n:
print('向左侧找！')
return dichotomy(min,mid,d,n)
else:
print('找到了%s'%d[mid])
return 
res = dichotomy(0,len(data),data,222)
print(res)

有位大佬说过：To Iterate is Human, to Recurse, Divine。

中文译为：人理解迭代，神理解递归。

可见递归是非常神奇的算法，它的神奇之处在于它允许用户用有限的语句描述无限的对象。

当然人无完人，递归也是有缺点的，它一般效率较低，且会导致调用栈溢出。

因为递归不断调用自身函数，且产生大量变量，而栈空间的容量是有限的，循环太多就会效率低下，甚至导致调用栈溢出。

以上が再帰的アルゴリズムをより深く理解するにはどうすればよいでしょうか? Pythonのサンプルを詳しく解説の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。