Python の一般的な正規化方法は何ですか?

データ正規化は、ディープ ラーニング データの前処理において非常に重要なステップであり、ディメンションを統一し、小さなデータが飲み込まれるのを防ぐことができます。

1: 正規化の概念

正規化とは、すべてのデータを [0,1] または [-1,1] に変換することです。目的は、注文をキャンセルすることです。データの各次元間の桁違いの大きさの違いにより、入力データと出力データの桁違いの大きさの差による過剰なネットワーク予測エラーを回避できます。

2: 正規化の役割

1. 後続のデータ処理の便宜のため、正規化により不必要な数値上の問題を回避できます。

2. プログラム実行時の収束を速くするために

3. 次元を統一します。サンプルデータは評価基準が異なるため、次元化して評価基準を統一することがアプリケーションレベルでの要件と考えられます。

4. ニューロンの飽和を避けてください。つまり、ニューロンの活性化が 0 または 1 に近い場合、これらの領域では勾配がほぼ 0 になるため、逆伝播プロセス中に局所的な勾配が 0 に近くなり、ネットワークにとって非常に不利になります。トレーニング。

5. 出力データ内の小さな値が飲み込まれないようにしてください。

3: 正規化の種類

1: 線形正規化

線形正規化は、minimum- 最大正規化、離散正規化とも呼ばれます。 ## は元のデータの線形変換であり、データ値を [0,1] にマッピングします。

#差分の標準化は、元のデータに存在する関係を保持し、ディメンションやデータ値の範囲の影響を排除する最も簡単な方法です。コードは次のように実装されます。

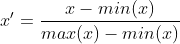
def MaxMinNormalization(x,Max,Min):
    x = (x - Min) / (Max - Min);
    return x

適用範囲: 比較的数値が集中する状況に適しています

欠点:

1. 最大値と最小値が不安定な場合、正規化された結果が不安定になりやすく、その後の使用効果も不安定になります。値の範囲が現在の属性 [min, max] を超える場合、システムはエラーを報告します。最小値と最大値を再決定する必要があります。

2. 値セット内の特定の値が非常に大きい場合、正規化された値は 0 に近くなり、あまり変わりません。 (1、1.2、1.3、1.4、1.5、1.6、10 など) このデータ セット。

2: ゼロ平均正規化 (Z スコア標準化)

Z スコア標準化は標準偏差標準化とも呼ばれ、処理されたデータの平均は 0 であり、標準偏差は 1 です。変換式は次のとおりです:

ここで、

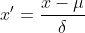
は元のデータの平均、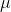 は元のデータの標準偏差であり、最も一般的に使用されます。標準化式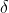

この方法では、元のデータの平均と標準偏差を与えて、データを標準化します。処理されたデータは標準正規分布に準拠します。つまり、平均は 0、標準偏差は 1 です。ここで重要なのは複合標準正規分布です。

コードは次のように実装されます:

def Z_ScoreNormalization(x,mu,sigma):
    x = (x - mu) / sigma;
    return x

3: 小数点判定 標準正規化

このメソッドは、属性値の小数点以下の桁を移動することによって、属性値を [-1,1] の間にマッピングします。移動される小数点以下の桁数は、絶対値の最大値によって異なります。属性値の値。変換式は次のとおりです。

4: 非線形正規化

この方法には対数、指数、正接が含まれます

適用範囲: 多くの場合、それデータ分析が比較的大規模なシナリオで使用されます。非常に大きい値もあれば、非常に小さい値もあります。元の値がマッピングされます。

4: バッチ正規化 (BatchNormalization)

1: はじめに

これまでのニューラルネットワークの学習では、入力層のデータのみを正規化していましたが、ニューラルネットワークには正規化処理がありません。中間層。入力データを正規化しましたが、入力データが

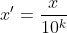
のように行列乗算された後は、ネットワークの層数が深くなるにつれて、そのデータ分布は大きく変化する可能性があります。データの流通はどんどん変わっていきます。したがって、トレーニング効果を高めるニューラル ネットワークの中間層でのこの正規化プロセスは、バッチ正規化 (BN) と呼ばれます。 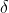#2: BN アルゴリズムの利点

人為的なパラメータの選択を減らします
学習率の要件を減らします。初期状態で大きな学習率を使用することも、より小さな学習率を使用することもできます。アルゴリズムは、収束するように訓練する。

2. #元のデータ分布を置き換え、過剰適合をある程度軽減します (トレーニングの各バッチで特定のサンプルが頻繁に選択されるのを防ぎます)

3. # # 勾配の消失を減らし、収束を高速化し、トレーニングの精度を向上させます。

4. 3: バッチ正規化 (BN) アルゴリズム プロセス

入力: 前の層の出力結果 X={x1,x2,...xm} 、学習パラメータ

,

アルゴリズム処理: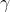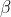1) 前層の出力データの平均値を計算します:

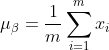
このうち、m はこのトレーニング サンプル バッチのサイズです。

2) 前の層の出力データの標準偏差を計算します:

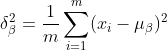
3) 正規化して

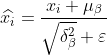を取得します。

式中の は、分母が 0 になるのを避けるために追加される 0 に近い小さな値です。

4) 再構築。上記の正規化プロセスの後に得られたデータを再構築し、次の結果を取得します。

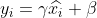
ここで、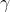、 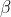は学習可能なパラメータです。

以上がPython の一般的な正規化方法は何ですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。