ホームページ >テクノロジー周辺機器 >AI >学ぶ=フィッティング?ディープラーニングと古典的な統計は同じものですか?
学ぶ=フィッティング?ディープラーニングと古典的な統計は同じものですか?
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB転載
- 2023-04-16 21:28:01784ブラウズ
この記事では、理論的コンピューター科学者でハーバード大学の著名な教授であるボアズ・バラク氏が、ディープラーニングと古典統計の違いを詳細に比較しています。 、成功した結果を無視することになります。「重要な要素」。
ディープ ラーニング (または機械学習一般) は、単なる統計として考えられることがよくあります。つまり、基本的には統計学者が研究するものと同じ概念ですが、統計とは異なる用語を使用して説明されます。ロブ・ティブシラニはかつて、この興味深い「用語集」を以下のように要約しました。

このリストの中に、本当に共感できるものはありますか?事実上、機械学習に関わる人なら誰でも、Tibshiriani が投稿した表の右側にある用語の多くが機械学習で広く使用されていることを知っています。
ディープラーニングを純粋に統計的な観点から理解すると、その成功の重要な要素を無視することになります。深層学習のより適切な評価は、完全に異なる概念を説明するために統計用語を使用することです。
ディープ ラーニングの適切な評価は、古い統計用語を説明するために別の用語を使用することではなく、これらの用語を使用してまったく異なるプロセスを説明することです。
この記事では、ディープ ラーニングの基礎が実際に統計と異なる、あるいは古典的な機械学習とさえ異なる理由を説明します。この記事では、まず、モデルをデータに適合させるときの「説明」タスクと「予測」タスクの違いについて説明します。次に、学習プロセスの 2 つのシナリオについて説明します: 1. 経験的リスク最小化を使用した統計モデルの適合; 2. 生徒への数学的スキルの指導。次に、記事ではどのシナリオがディープラーニングの本質に近いのかについて説明します。
深層学習の数学とコードは統計モデルのフィッティングとほぼ同じですが。しかし、より深いレベルでは、ディープラーニングは生徒に数学のスキルを教えることに似ています。そして、「私は深層学習の理論を完全にマスターしました!」とあえて主張する人はほとんどいないはずです。実際のところ、そのような理論が存在するかどうかは疑わしい。むしろ、ディープラーニングのさまざまな側面はさまざまな視点から理解するのが最もよく、統計だけでは完全な全体像を提供することはできません。
この記事ではディープラーニングと統計を比較していますが、ここでいう統計とは、最も古くから研究され、教科書にも載っている「古典統計」を特に指します。 20 世紀の物理学者が古典物理学の枠組みを拡張する必要があったのと同じように、多くの統計学者がディープラーニングと非古典的な理論的手法に取り組んでいます。実際、コンピュータ科学者と統計学者の間の境界線を曖昧にすることは、双方に利益をもたらします。
予測とモデルのフィッティング
科学者は常にモデルの計算結果と実際の観測結果を比較して、モデルの精度を検証してきました。エジプトの天文学者プトレマイオスは、惑星運動の独創的なモデルを提案しました。プトレマイオスのモデルは天動説に従いましたが、一連の周転円 (以下の図を参照) を備えており、優れた予測精度を実現しました。対照的に、コペルニクスの元の地動説モデルはプトレマイオスのモデルよりも単純でしたが、観測を予測する精度は低かったです。 (コペルニクスは後にプトレマイオスのモデルと比較できるように独自の周転円を追加しました。)
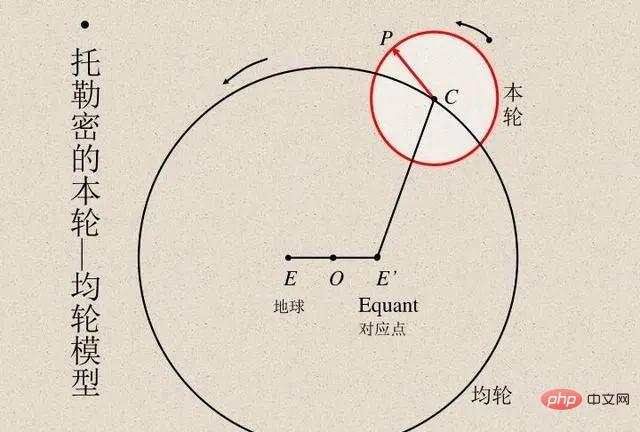
プトレマイオスのモデルとコペルニクスのモデルはどちらも比類のないものでした。 「ブラックボックス」を通じて予測を行いたい場合は、プトレマイオスの地心モデルの方が優れています。しかし、「内部を見る」ことができる単純なモデル (星の運動を説明する理論の出発点です) が必要な場合は、コペルニクスのモデルが最適です。その後、ケプラーはコペルニクスのモデルを楕円軌道に改良し、ケプラーの惑星運動の三法則を提案し、ニュートンは地球に適用できる重力の法則で惑星法則を説明できるようになりました。
したがって、地動説モデルは予測を提供する単なる「ブラック ボックス」ではなく、いくつかの単純な数学方程式によって与えられますが、方程式には「変動部分」がほとんどないことが重要です。天文学は長年にわたり、統計手法を開発するためのインスピレーションの源でした。ガウスとルジャンドルは、小惑星やその他の天体の軌道を予測するために、1800 年頃に独立して最小二乗回帰を発明しました。 1847 年にコーシーは勾配降下法を発明しましたが、これも天文学的な予測が動機となっていました。
物理学では、学者がすべての詳細を習得して「正しい」理論を見つけ、予測の精度を最大化し、データの最良の説明を提供できる場合があります。これらはオッカムの剃刀などの考え方の範囲内であり、単純さ、予測力、説明力がすべて調和していると考えることができます。
しかし、他の多くの分野では、説明と予測という 2 つの目標の関係はそれほど調和していません。観測値を予測したいだけの場合は、「ブラック ボックス」を通過するのがおそらく最善です。一方、因果モデル、一般原理、重要な特徴などの説明情報を取得したい場合は、理解して説明できる単純なモデルの方が良いでしょう。
モデルの正しい選択は、その目的によって異なります。たとえば、多くの個人 (例: 何らかの病気) の遺伝子発現と表現型を含むデータセットを考えます。目標が人が病気になる可能性を予測することである場合、データセットがどれほど複雑で、どれだけ多くの遺伝子に依存しているかは関係ありません。 、タスクに適応した最適な予測モデルを使用します。逆に、さらなる研究のためにいくつかの遺伝子を同定することが目的の場合、複雑で非常に正確な「ブラック ボックス」の用途は限られています。
統計学者レオ・ブライマンは、統計モデリングの 2 つの文化に関する有名な 2001 年の記事でこの点を述べました。 1 つ目は、データを説明できるシンプルな生成モデルに重点を置く「データ モデリング文化」です。 2 つ目は、データがどのように生成されたかにとらわれず、どんなに複雑であってもデータを予測できるモデルを見つけることに重点を置く「アルゴリズム モデリング文化」です。

論文のタイトル:
統計モデリング: 2 つの文化
論文のリンク:
https://projecteuclid .org/euclid.ss/1009213726
ブライマンは、統計は第一次文化に支配されすぎており、この焦点が次の 2 つの問題を引き起こすと考えています:
- 無関係な理論と疑わしい科学的結論につながるブライマンの論文は、発表されたとき、いくつかの論争を引き起こしました。同じく統計学者のブラッド・エフロン氏は、いくつかの点には同意するものの、ブライマン氏の議論は複雑な「ブラックボックス」を作成するために多大な労力を費やすことを支持し、倹約と科学的洞察に反するようだと強調した。しかし、最近の記事でエフロン氏は以前の見解を放棄し、「21世紀の統計学の焦点は予測アルゴリズムにあり、ブライマン氏の提案に沿って大幅に進化した」ため、ブライマ氏の方が先見の明があったことを認めた。
- 古典的な予測モデルと最新の予測モデル
 1992 年、Geman、Bienenstock、Doursat はニューラル ネットワークに関する悲観的な記事を書き、「現在のフィードフォワード ニューラル ネットワークは、機械の知覚と機械学習における困難な問題を解決するにはほとんど不十分である」と主張しました。具体的には、汎用ニューラルネットワークは困難なタスクの処理には成功せず、成功できる唯一の方法は人工的に設計された機能を使用することだと主張しています。彼らの言葉を借りれば、「重要な特性は、統計的な意味で学習するのではなく、組み込まれているか、「組み込まれている」必要があります。」 今のところ、Geman らは完全に間違っているように見えますが、理解することはより興味深いです。なぜ彼らは間違っているのか。
1992 年、Geman、Bienenstock、Doursat はニューラル ネットワークに関する悲観的な記事を書き、「現在のフィードフォワード ニューラル ネットワークは、機械の知覚と機械学習における困難な問題を解決するにはほとんど不十分である」と主張しました。具体的には、汎用ニューラルネットワークは困難なタスクの処理には成功せず、成功できる唯一の方法は人工的に設計された機能を使用することだと主張しています。彼らの言葉を借りれば、「重要な特性は、統計的な意味で学習するのではなく、組み込まれているか、「組み込まれている」必要があります。」 今のところ、Geman らは完全に間違っているように見えますが、理解することはより興味深いです。なぜ彼らは間違っているのか。
ディープラーニングは他の学習方法とは確かに異なります。ディープ ラーニングは最近傍法やランダム フォレストのように単なる予測のように見えるかもしれませんが、より複雑なパラメーターを持っている場合があります。これは質的な違いではなく、量的な違いであるように思えます。しかし、物理学ではスケールが数桁変わると、まったく異なる理論が必要になることが多く、ディープラーニングでも同様です。深層学習と古典的なモデル (パラメトリックまたはノンパラメトリック) の基礎となるプロセスは完全に異なりますが、それらの数式 (および Python コード) は高レベルでは同じです。
この点を説明するために、統計モデルを当てはめるシナリオと生徒に数学を教えるシナリオという 2 つの異なるシナリオを考えてみましょう。
シナリオ A: 統計モデルの近似
(
はの行列です;
は次元ベクトル、つまりカテゴリ ラベルです。データが構造を持ちノイズを含むモデルからのものであると考えると、フィッティング対象のモデルになります)
2. 上記のデータを使用してモデルを当てはめ、 最適化アルゴリズムを使用して経験的リスクを最小限に抑えます。つまり、
最適化アルゴリズムを使用して経験的リスクを最小限に抑えます。つまり、 が最小となり、
が最小となり、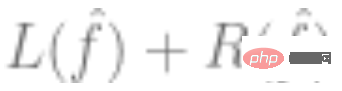 が損失 (予測値が真の値にどの程度近いかを示す) を表し、
が損失 (予測値が真の値にどの程度近いかを示す) を表し、 がオプションになるように、最適化アルゴリズムを通じてそのような
がオプションになるように、最適化アルゴリズムを通じてそのような  を見つけます。正則化用語。
を見つけます。正則化用語。
3. モデルの全体的な損失が小さければ小さいほど良い、つまり汎化誤差 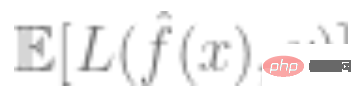 の値は比較的最小になります。
の値は比較的最小になります。
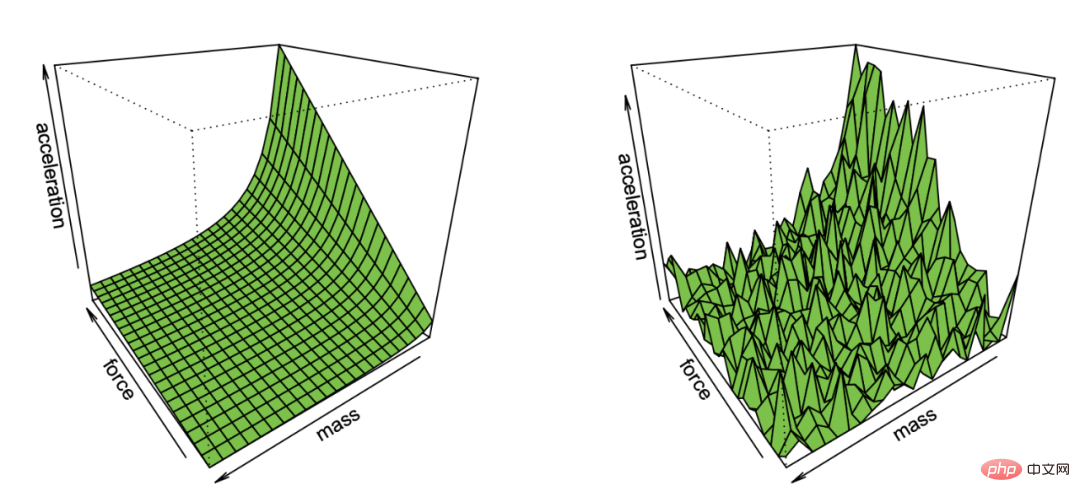
Effron ノイズを含む観測からニュートンの第一法則を復元するデモンストレーション
この非常に一般的な例には、実際には最小二乗法、線形回帰、最近傍法などの多くの内容が含まれています。 、ニューラルネットワークトレーニングなど。古典的な統計シナリオでは、通常、次のような状況に遭遇します。
トレードオフ: 最適化されたモデルのコレクションを仮定します (関数が非凸であるか、正則化項が含まれている場合は、アルゴリズムと正則化を慎重に選択する必要があります)。モデル セット。偏差は、要素が達成できる真の値に最も近い近似値です。セットが大きいほど、偏差は小さくなり、0 (の場合) になる可能性があります。
ただし、セットが大きいほど、 、そのメンバーのサイズは小さくなります。範囲内のサンプルが多いほど、アルゴリズム出力モデルの分散は大きくなります。全体的な汎化誤差は、バイアスと分散の合計です。したがって、統計学習は通常、バイアス分散です。実際、Geman らは、バイアスと分散のジレンマによってもたらされる基本的な制限が、以下を含むすべてのノンパラメトリック推論モデルに当てはまると主張することで、ニューラル ネットワークに対する悲観的な見方を示しています。
「多ければ多いほど良い」は必ずしも当てはまりません: 統計学習では、より多くの特徴やデータが必ずしもパフォーマンスを向上させるわけではありません。たとえば、多くの無関係な特徴を含むデータから学習することは困難です。混合モデルからデータが得られる場合、データが 2 つの分布 ( や など) のいずれかから得られることは、それぞれの分布を個別に学習するよりも困難です。
収穫逓減: 多くの場合、予測ノイズを減少させるために必要なデータ ポイントの数は、レベルはパラメーターの合計と同じです 関連する、つまり、データ ポイントの数は にほぼ等しい この場合、開始するには約 k 個のサンプルが必要ですが、一度そうしてしまうと、収穫が逓減することに直面します。 90% の精度を達成するには k ポイントが必要ですが、精度を 95% に高めるには約追加のポイントが必要です。一般的に言えば、リソース (データ、モデルの複雑さ、計算のいずれであっても) が増加するにつれて、特定の新しい機能を解放するのではなく、ますます細かい区別を取得することを望むようになります。
損失とデータへの依存度が高い: モデルを高次元データに適合させるとき、どんな小さなディテールでも大きな違いが生じる可能性があります L1 または L2 正則化器などの選択 まったく異なるデータセットを使用することは言うまでもなく、非常に重要です高次元オプティマイザの数が異なると、互いに大きく異なります。
データは比較的「単純」です。通常、データはいくつかの分布から独立していると想定されます。分布はサンプリングされます。ポイントは次の値に近いですが、決定境界は分類が困難ですが、高次元での測定集中の現象を考慮すると、ほとんどの点の距離は類似していると考えられます。したがって、古典的なデータ分布では、データ点間の距離の差はわずかですが、 , 混合モデルはこの違いを示す可能性があるため、上記の他の問題とは異なり、この違いは統計では一般的です。
シナリオ B: 数学の学習
このシナリオでは、あなたが数学を教えることを想定しています。いくつかの指示と演習を通じて、学生に数学 (導関数の計算など) を教えます。このシナリオは、正式には定義されていませんが、いくつかの定性的特徴があります:
能力の向上から自動化された表現へ: 場合によっては問題解決の成果が逓減することもありますが、学生はいくつかの段階を経て学習します。いくつかの問題を解決することで概念を理解し、新しい能力を解放できるステージがあります。さらに、生徒が特定のタイプの問題を繰り返すと、同様の問題を見たときに自動化された問題解決プロセスが形成され、以前の能力向上から自動問題解決に変わります。
パフォーマンスはデータや損失に依存しません: 数学的概念を教える方法は複数あります。異なる書籍、教育方法、または成績評価システムを使用して学習した生徒は、最終的には同じ内容を学習し、同様の数学的能力を身につけることができます。
一部の問題はより難しい: 数学の演習では、異なる生徒が同じ問題を解く方法の間に強い相関関係があることがよく見られます。問題には固有の難易度があり、学習に最適な自然な難易度の進行があるようです。
ディープ ラーニングは、統計的推定や学生の学習スキルに重点を置いたものですか?
上記の 2 つの比喩のうち、現代の深層学習を説明するのに適切なのはどれですか?具体的には何が成功の秘訣なのでしょうか?統計モデルのフィッティングは、数学とコードを使用して適切に表現できます。実際、標準的な Pytorch トレーニング ループは、経験的なリスクの最小化を通じて深いネットワークをトレーニングします。

より深いレベルでは、これら 2 つのシナリオの関係は明確ではありません。より具体的には、具体的な学習課題を例として挙げます。 「自己教師あり学習線形検出」手法を使用してトレーニングされた分類アルゴリズムを考えてみましょう。具体的なアルゴリズムのトレーニングは次のとおりです:
1. データがシーケンスであると仮定します。ここで、 は特定のデータ ポイント (画像など) であり、ラベルです。
は特定のデータ ポイント (画像など) であり、ラベルです。
2. まず、関数 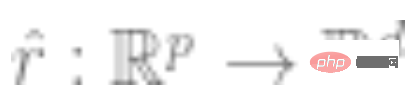 を表すディープ ニューラル ネットワークを取得します。ある種の自己教師あり損失関数は、ラベルではなくデータ ポイントのみを使用して最小化することによってトレーニングされます。このような損失関数の例としては、再構成 (入力を他の入力で復元する) や対照学習 (基本的な考え方は、特徴空間内の正のサンプルと負のサンプルを比較して、サンプルの特徴表現を学習することです) があります。
を表すディープ ニューラル ネットワークを取得します。ある種の自己教師あり損失関数は、ラベルではなくデータ ポイントのみを使用して最小化することによってトレーニングされます。このような損失関数の例としては、再構成 (入力を他の入力で復元する) や対照学習 (基本的な考え方は、特徴空間内の正のサンプルと負のサンプルを比較して、サンプルの特徴表現を学習することです) があります。
3. 完全なラベル付きデータを使用して線形分類器 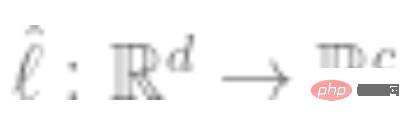 (クラスの数) を近似し、クロスエントロピー損失を最小限に抑えます。最後の分類器は次のとおりです。
(クラスの数) を近似し、クロスエントロピー損失を最小限に抑えます。最後の分類器は次のとおりです。
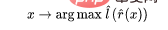
ステップ 3 は線形分類器に対してのみ機能するため、「魔法」はステップ 2 (深層ネットワークの自己教師あり学習) で起こります。自己教師あり学習には、いくつかの重要な特性があります:
関数を近似するのではなくスキルを学習する: 自己教師あり学習は、関数を近似することではなく、さまざまな下流で使用できる表現を学習することです。タスク (これは自然言語処理の主要なパラダイムです)。線形プローブ、微調整、または励起を通じて下流タスクを取得することは二次的なものです。
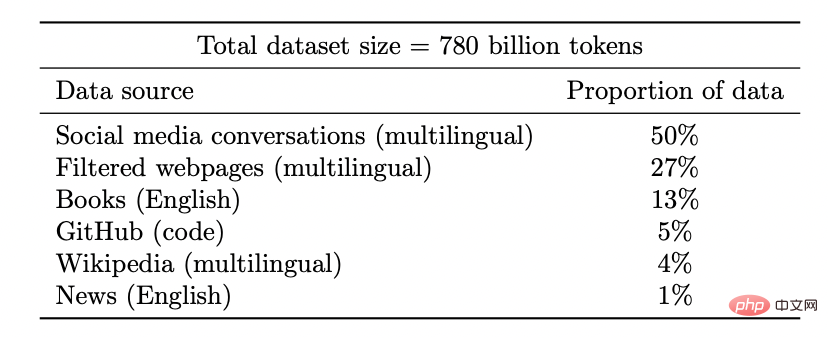
多ければ多いほど良い: 自己教師あり学習では、データ量が増加するにつれて表現の品質が向上し、複数のソースからのデータを混合しても表現の品質が悪化することはありません。実際、データは多様であればあるほど良いのです。
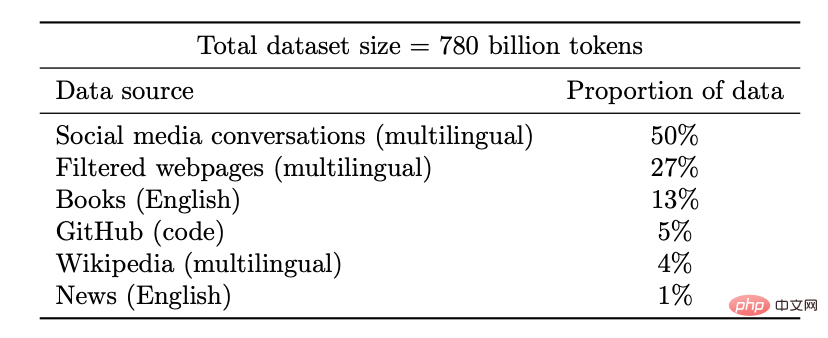
Coogle PaLM モデルのデータセット
新機能のロック解除: リソース (データ、コンピューティング、モデル サイズ) への投資が増加するにつれて、ディープ ラーニング モデルも不連続に改善していく。これは、いくつかの組み合わせ環境でも実証されています。
モデルのサイズが大きくなるにつれて、PaLM はベンチマークで個別の改善を示し、ジョークがなぜ面白いのかを説明するなど、驚くべき機能を解放します。
パフォーマンスは損失やデータからほぼ独立しています。複数の自己監視損失があり、さまざまなコントラストおよび再構成損失が実際に画像研究で使用され、言語モデルは片面再構成を使用します (次のトークンを予測します)。または、マスク モデルを使用して、左右のトークンからマスク入力を予測します。わずかに異なるデータセットを使用することも可能です。これらは効率に影響を与える可能性がありますが、「合理的な」選択が行われている限り、多くの場合、使用される特定の損失やデータセットよりも元のリソースの方が予測パフォーマンスが向上します。
一部のケースは他のケースよりも困難です。この点は自己教師あり学習に特有のものではありません。データポイントには固有の「難易度」があるようです。実際、異なる学習アルゴリズムには異なる「スキル レベル」があり、異なるデータには異なる「難易度レベル」があります (分類器がポイントを正しく分類する確率は、スキルに応じて単調に増加し、難易度に応じて単調に減少します)。
「スキル vs 難易度」パラダイムは、Recht らと Miller らによって発見された「ライン上の精度」現象を最も明確に説明したものです。 Kaplen、Ghosh、Garg、Nakkiran による論文では、データセット内のさまざまな入力が、一般的にさまざまなモデル ファミリに対して堅牢な固有の「難易度プロファイル」をどのように持つかを示しています。
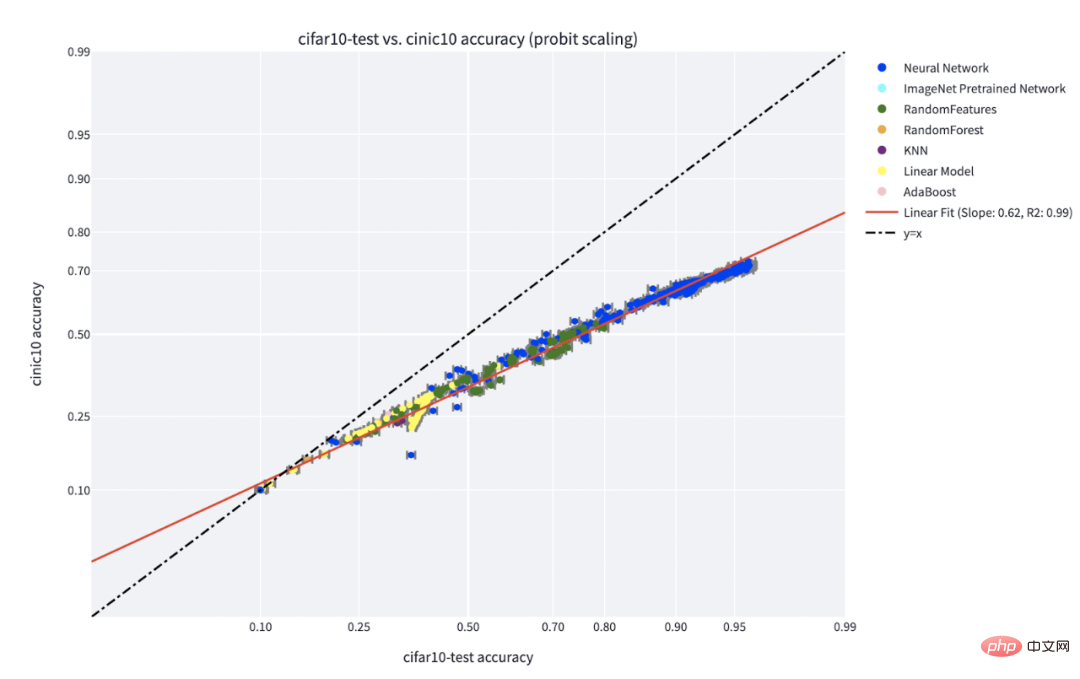
C** IFAR-10 でトレーニングされ、CINIC-10 でテストされた分類器のライン現象の精度。図のソース: https://millerjohnp-linearfits-app-app-ryiwcq.streamlitapp.com/
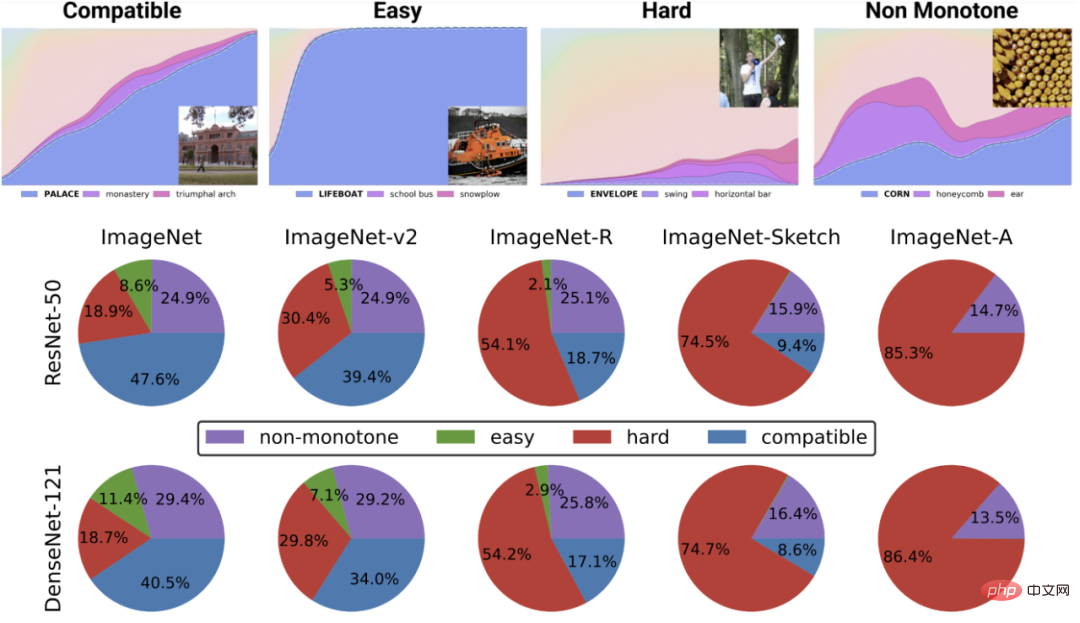
上の図は、最も可能性の高いクラスのさまざまなソフトマックス確率を示しています。トレーニング時間によってインデックス付けされたクラスの分類器のグローバル精度の関数。下の円グラフは、さまざまなデータセットをさまざまなタイプの点に分解したものを示しています (この分解はさまざまな神経構造でも同様であることに注意してください)。
トレーニングは教えることです: 現代の大規模モデルのトレーニングは、モデルをデータに適合させるというよりも、学生に教えることに近いようです。学生が理解できない場合や疲れを感じた場合、学生は「休む」か、別の方法を試します(トレーニングの違い)。 Meta の大規模なモデル トレーニング ログは有益です。ハードウェアの問題に加えて、トレーニング中のさまざまな最適化アルゴリズムの切り替え、「ホット スワップ」アクティベーション関数 (GELU から RELU) の検討などの介入も確認できます。モデルのトレーニングを表現の学習ではなく、データのフィッティングと考える場合、後者はあまり意味がありません。
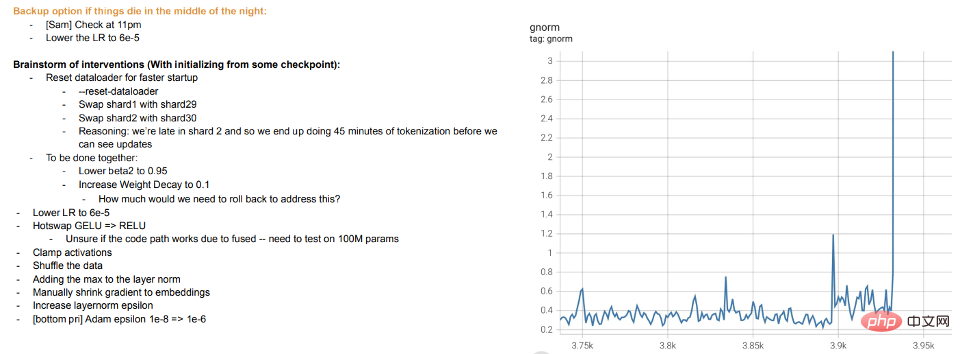
メタ トレーニング ログの抜粋
4.1 しかし、教師あり学習についてはどうでしょうか?
自己教師あり学習については前述しましたが、深層学習の代表的な例はやはり教師あり学習です。結局のところ、ディープラーニングの「ImageNet モーメント」は ImageNet から生まれました。では、上で説明した内容はこの設定にも当てはまりますか?
まず、教師あり大規模深層学習の出現は、大規模で高品質のラベル付きデータセット (つまり ImageNet) が利用可能になったことにより、ある意味偶然でした。想像力が豊かであれば、ディープラーニングが最初に教師なし学習を通じて自然言語処理にブレークスルーをもたらし始め、その後、ビジョンと教師あり学習に移行したという別の歴史を想像することができます。
第二に、完全に異なる損失関数を使用しているにもかかわらず、教師あり学習と自己教師あり学習が「内部的に」同様に動作するという証拠があります。通常、どちらも同じパフォーマンスを達成します。具体的には、それぞれについて、自己監視でトレーニングされた深さ d のモデルの最初の k 層と、教師ありモデルの最後の d-k 層を、パフォーマンスをほとんど損なうことなく組み合わせることができます。
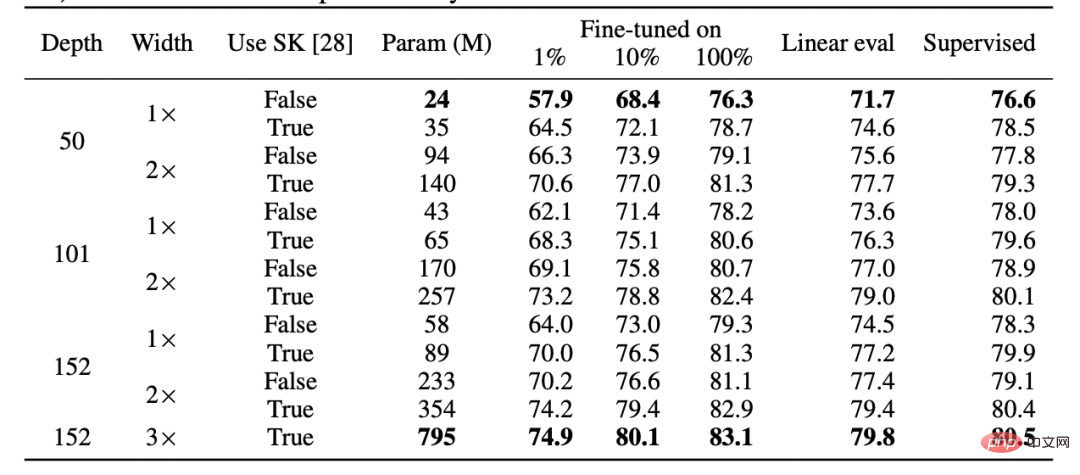
SimCLR v2 論文の表。教師あり学習、微調整された (100%) 自己教師あり、および自己教師あり線形検出のパフォーマンスは一般的に類似していることに注意してください (出典: https://arxiv.org/abs/2006.10029)
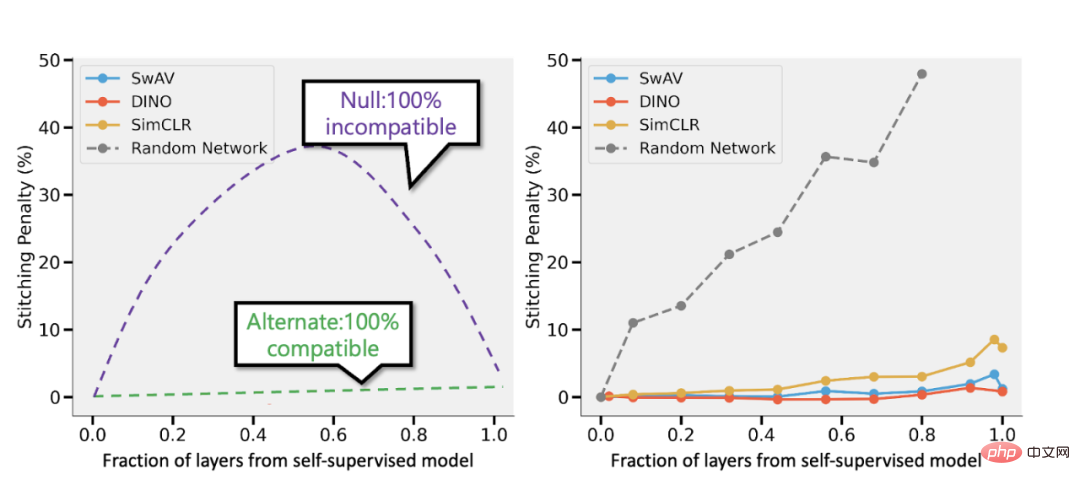
自己教師ありモデルと Bansal らの教師ありモデル (https://arxiv.org/abs/2106.07682) を接続します。左: 自己教師ありモデルの精度が教師ありモデルより (たとえば) 3% 低い場合、完全に互換性のある表現では、レイヤーの p 部分が自己教師ありモデルからのものである場合、p 3% のスプライシング ペナルティが発生します。モデル。モデルに完全な互換性がない場合、より多くのモデルがマージされるため、精度が大幅に低下することが予想されます。右: さまざまな自己教師ありモデルを組み合わせた実際の結果。
自己教師あり単純モデルの利点は、特徴学習または「深層学習マジック」(深層表現関数によって実行される)と統計モデル フィッティング (ここでは線形またはその他の完成した「単純な」分類器によって表されます)を組み合わせることができることです。上)分離。
最後に、これは推測にすぎませんが、実際には、「メタ学習」は学習表現と同一視されることが多いようです (https://arxiv.org/abs/1909.09157、https: //arxiv .org/abs/2206.03271)、これは、モデル最適化の目標に関係なく、これが主に行われていることを示すもう 1 つの証拠と見なすことができます。
4.2 過剰なパラメータ化についてはどうすればよいですか?
この記事では、統計学習モデルと実際の深層学習の違いの古典的な例と考えられるもの、つまり「バイアスと分散のトレードオフ」の欠如と、過剰にパラメータ化されたモデルが適切に一般化できる能力については省略します。 。
なぜスキップするのでしょうか?理由は 2 つあります:
- まず、教師あり学習が実際に自己教師あり単純学習と同等である場合、これでその汎化能力が説明できる可能性があります。
- 第二に、過剰なパラメータ化は深層学習の成功の鍵ではありません。ディープネットワークが特別なのは、サンプル数に比べてネットワークが大きいということではなく、絶対的に大きいということです。実際、通常、教師なし/自己教師あり学習では、モデルが過剰にパラメーター化されることはありません。非常に大規模な言語モデルであっても、そのデータセットはさらに大きくなります。

Nakkiran-Neyshabur-Sadghi の「ディープ ブートストラップ」論文では、現代のアーキテクチャが「過剰パラメータ化」または「不足サンプリング」領域でも同様に動作することを示しています (モデルは過学習するまで、限られたデータ上で複数のエポックをトレーニングします: 上の図の「現実世界」)、「パラメータ不足」または「オンライン」状態でも (モデルは単一エポックでトレーニングされ、各サンプルは表示されるだけです)かつて: 上の写真の「理想の世界」)。図の出典: https://arxiv.org/abs/2010.08127
概要
統計学習は確かに深層学習において役割を果たします。ただし、同様の用語とコードを使用しているにもかかわらず、深層学習を古典的なモデルよりも多くのパラメーターでモデルをフィッティングするだけであるとみなすと、その成功に重要な多くのことが無視されます。生徒に数学を教えるための比喩も完璧ではありません。
生物進化と同様、深層学習には再利用されたルール (経験損失を伴う勾配降下法など) が多数含まれていますが、非常に複雑な結果が生成される可能性があります。ネットワークのさまざまなコンポーネントが、さまざまな時点で、表現学習、予測フィッティング、暗黙的な正則化、純粋なノイズなど、さまざまなことを学習しているようです。研究者たちは、深層学習に関する質問に答えるどころか、質問するための適切なレンズを依然として探しています。
以上が学ぶ=フィッティング?ディープラーニングと古典的な統計は同じものですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

