ホームページ >テクノロジー周辺機器 >AI >チューリングマシン: コンピューターが存在しない状況で、どうやってコンピューティングについて語ることができるでしょうか?
チューリングマシン: コンピューターが存在しない状況で、どうやってコンピューティングについて語ることができるでしょうか?
- PHPz転載
- 2023-04-16 14:34:031599ブラウズ
1950年10月、「機械は考えることができるか」というタイトルの論文が発表されました。この論文は、通信装置を介して被験者にランダムに質問をし、被験者が被験者の意図を推測するよう求めることで、被験者と被験者(生身の人間と機械)を切り離すという恐ろしいテストを提案しています。話していたのは生身の人間か機械でした。
複数のテストの後、マシンが各参加者に平均 30% 以上の誤った判断をさせることができれば、マシンはテストに合格し、人間の能力を備えていると見なされます。
これは、ロボットが人間の知性を持っている可能性があることに人々が初めて気づいたときです。このテストは、何百万もの SF 愛好家の間で話題になっているチューリング テストです。この論文により、著者アラン・チューリングは「人工知能の父」の称号を獲得しました。
人工知能への道、またはコンピュータ開発の歴史の起源は、チューリングが 24 歳のときに発表した論文です。この論文の中で、彼は「計算可能性」に厳密な数学的定義を与え、有名な「チューリングマシン」のアイデアを提案しました。チューリング マシンは特定のマシンではなく、想像できるすべての計算可能な関数を計算するために使用できる、非常にシンプルだが非常に強力なコンピューティング デバイスを作成できるメンタル モデルです。
チューリングはチューリング マシンを発明したため、時々、チューリングが実際に「コンピューターを発明した」と主張する人がいます。ただし、チューリング マシンは実際のコンピューティング マシンと同じように設計されているわけではありません。チューリング マシンはマシンの抽象モデルですらない。 (チューリングの発言によって証明されるように)チューリングマシンはテーブル上の紙に書いている人をモデルにしたものであることが判明しました。では、チューリングはなぜチューリング マシンを発明したのでしょうか、そしてチューリング マシンは私たちをどこへ導くのでしょうか?
1 チューリングの論文「計算可能な数について」
これらの質問に答える最良の方法は、教科書を脇に置いて、紙を開くことです。現在、1936 年の定期刊行物を借りるには、ローン カードに記入する必要も、図書館員が図書館から本を取りに来るまで 1 時間待つ必要もありません。必要なのはモルト ウイスキーのグラスを手に持ち、自宅で Google に簡単にアクセスできることだけです。私たちが探しているチューリング論文は次のとおりです:

論文アドレス: https://www.cs.virginia.edu/ ~robins/Turing_Paper_1936.pdf
論文にはいくつかの誤りがありますが、欠点が欠点を上回るほどではありません。 Joel David Hamkins が述べたように、チューリングは計算可能な実数を、計算可能な 10 進展開を伴う数値として定義しました。これは実際には機能しませんが、修正するのは難しくありません。
チューリングは、「決定問題における計算可能な数とその応用について」というタイトルでこの論文を書いた意図を説明しました。その中の「Entscheidungsproblem (決定問題)」は問いかけます。与えられた 1 次論理式が有効である、つまりすべての解釈で真であると判断するための効率的な手法があるかどうか。
チューリングは、次のようにアイデアを発展させました:
実数を計算している人を、限られた数の条件しか満たせないマシンにたとえることができます。q1、q2、... qR.... このマシンには 1 つだけあります。その中を「紙テープ」が通過し、紙テープはいくつかの部分に分割されます。これらの部分を正方形と呼び、それぞれの正方形には「記号」を入れることができます...書き留める人もいます記号は実数の10進数の列を形成します他の記号は「記憶を助ける」ためのラフなメモです。このラフなメモは消すことができます。私の主張は、このテープ上の滑りです。特定の記号を前後にスワイプして記号を処理するという操作方法です」
……
## 「計算可能な数値」とは、単に 10 進表現が計算できる実数を意味します。私の定義によれば、数値の 10 進表現を機械で書き記すことができれば、その数値は計算可能です。
チューリングはその後、それを定義し、証明しました。これは典型的な数学の論文であり、典型的な工学論文ではありません。この種の記事では、読者はその記事で説明されている特定のメカニズムを実装する方法についての議論を見たいと考えています。チューリングのタイトルと記事から、チューリングの主な関心事であることがわかります。小数点以下無限桁までの実数の計算。 この論文には他にも多くの重要な貢献があります: この論文を書いた後、チューリングは理論的な計算科学を開拓しました。畑への門。 チューリングがユニバーサル チューリング マシン (UTM) のアイデアを思いついた理由はわかりませんが、かつて考えてみれば、彼は普遍的なチューリングマシンの存在が明らかだと思っているかもしれません。チューリング マシンの目的は、机で働く事務員をシミュレートすることであり、チューリング マシンの操作は事務員の操作と同じであり、マシンに基づいて指定された変換規則のリストに従って特定の操作を実行します。状態とテープのシンボル - このような日常的なタスクを実行するにはチューリング マシンが明らかに必要です。チューリングの論文は構造の詳細について少し大雑把だったが、誰も気にしていないようだった。 鋭く鮮やかにデザインされた万能チューリングマシンが誕生しました。数十年前、ケンブリッジ大学でケン ムーディ博士が普遍的なミンスキー キー生成を作成しました: リンク: http://www .igblan.free-online.co.uk/igblan/ca/minsky.html このようなマシンのレジスターは限られており、各レジスターには任意の大きな非負整数を格納できます。これには、3 つの異なるタイプのラベル命令で構成される有限プログラムがあります。 と N×N の間の標準的な全単射を使用して、整数のリストを 1 つの整数にパックします。彼は、スタックのプッシュアップやポップオフなどの操作を実行する小さなレジスタ マシンの小さなライブラリを作成し、実際のプロセッサのフェッチと実行のサイクルを彷彿とさせる設計を作成しました。プロセス全体は次のスライドでご覧いただけます。下の写真はマシン自体です。 下の写真はマシンの全体構造です。 (これら 2 つの写真の作者は、ケンブリッジ大学の理論計算科学教授である Andrew Pitts です。) 驚くべきことに、この構造は機械はとてもシンプルです! 停止問題は明らかに決定不可能です。そうしないと、フェルマーの最終定理など、多くの数学的予想を解くのが難しくなります。x、y、z、n>2 を検索し、 一般的な考えに反して、チューリングの論文では停止問題については議論されていませんでしたが、彼が「循環性」と呼んだ、停止問題に関連する特性について議論しました。チューリング マシンが「限られた数の最初のシンボル (つまり 0 と 1) のみを書き込む」場合、チューリング マシンは循環的です。周期性が重要な理由は、チューリングが実数を無限のバイナリ文字列として近似することを特に好んでいたからだと思います。物理学者のクリストファー・ストレイチーは、1965 年のコンピューター・ジャーナルへの手紙の中で、チューリングが停止問題の決定不可能性の証拠を教えてくれたと主張した。 2009年9月、デヴィッド・P・アンダーソンはモーリス・ウィルクスにインタビューしましたが、彼のチューリングに対する見方は世間とはまったく逆でした: David P. Anderson: 決定問題に関するチューリングの 1936 年の論文の重要性は何だと思いますか? Maurice Wilkes: エンジニアはストアド プログラムのアイデアを一種の聖なる三位一体として見て、こう言うと思います。それがどのように行われるべきかです。」 その論文のアイデアと私が述べたことの間に実質的な違いはありません。彼がその論文を出版できたのは幸運でした。つまり、アロンゾ・チャーチは他の方法を使って同じ結果を得ました。 記事アドレス: https://cacm.acm.org/magazine/2009/9/38898-an-interview-with -maurice-wilkes/fulltext ##なお、モーリス ウィルクス氏はインタビュー時点で 96 歳であり、彼自身もコンピュータのパイオニアとして有名な EDSAC (Electronic電子遅延ストレージ自動計算機 Delay Storage Auto Calculator の生みの親。彼の奇妙な答えには、チューリングの高貴な地位に対する彼の嫉妬が見て取れます。この二人は明らかに気が合わない!モーリス・ウィルクスの理論軽視も見られます。プログラムを組み込んだコンピューターでは機械を数値にエンコードすることが期待されていましたが、チューリングの研究は純粋な数学であり、工学的な意味はありませんでした。チューリングは実際のコンピュータ工学に興味を持っていましたが、実際のプロジェクトに参加しようとする試みは何度も挫折しました。 そして、教会に関するこれらの発言をどのように評価しますか? チューリングが研究を行っている間、多くの研究者が「効率的な計算可能性」という考えに注目しました。ここで私は読者に Qiu Qi 著『初級整数論の解けない問題』を読むことをお勧めします (下の図を参照)。 ペーパーリンク: https://www.jstor.org/stable/2371045?origin=crossref 正直に言うと、この論文は読みにくいですが、私たちを現場に連れて行ってくれます。この記事では、λ 計算の定義、再帰関数 (クリーネ/ゲーデルの意味で) の定義、および λ 計算におけるパラダイムの存在と同等性に関するいくつかの議論の余地のない質問を示します。チャーチとクレイニーはラムダ定義可能な関数と再帰関数が等価であることを証明し、チューリングがプリンストンにいた間にラムダ定義可能な関数とチューリングで計算できる関数の間の等価性も証明されていたので、チャーチとチューリングのテーゼが得られます。これは、効果的に計算可能な関数がまさに数学的同値類の関数であるという事実を指します。 よく言われることですが、「効率的に計算可能」というのは正確な概念ではないため、この命題が正しいかどうかを証明することはできません。チューリングの計算可能な関数は、宇宙の存続期間内には計算できない関数が多数含まれているため、かなり包括的なクラスとして考えることができます。 Ackermann 関数の助けを借りて、例を簡単に取得できます。 アッカーマン関数の現代形式は次のとおりです: 記事リンク: https://lawrencecpaulson.github.io/2022/02/09/Ackermann-example.html f(n)=A(n,n) と定義すると、偶数 f(4) の計算は期待できません。 g(n)=A(4,n) は、原始的な再帰ではありますが、計算するのはほとんど不可能です。 1930 年代までデジタル コンピューターはありませんでしたが、効率的な計算能力の概念は数学者にはよく知られていました。妥当性の概念はギリシャ幾何学の直線構造とコンパス構造に古くから登場しており、決定問題やヒルベルトの第 10 問題にも不可欠な部分です。ゲーデルの再帰関数やチャーチのラムダ計算と比較したときのチューリングの概念の優れた点は、それが明らかに正しいということです。ゲーデル自身も、彼の再帰関数が計算の概念を捉えているかどうかはわかりませんでしたし、チャーチの考えが正しかったかどうかもわかりません。チューリングのアイデアだけがシンプルで自然でした。チューリングのアイデアは他のモデルと同等であることが証明されており、それらすべてに合理的な説明を提供します。彼は 1937 年の論文「計算可能性とラムダ定義可能性」でこの事実を指摘しました。 この記事は、著者が提案した 計算可能関数 が Qiu Qi の λ 定義可能関数 および提案された関数 と一致することを証明することを目的としています。 Elbrown と Brother による Del によって提案され、Kleiny によって開発された 一般再帰関数 は同じです。これらの同じ関数は、X で定義されたすべての関数が計算可能であり、すべての計算可能な関数が一般に再帰的であることを証明します。 チューリングは「計算可能」と書きましたが、「チューリング計算可能」と書かなければならないことに注意してください。
2 ユニバーサル チューリング マシン

N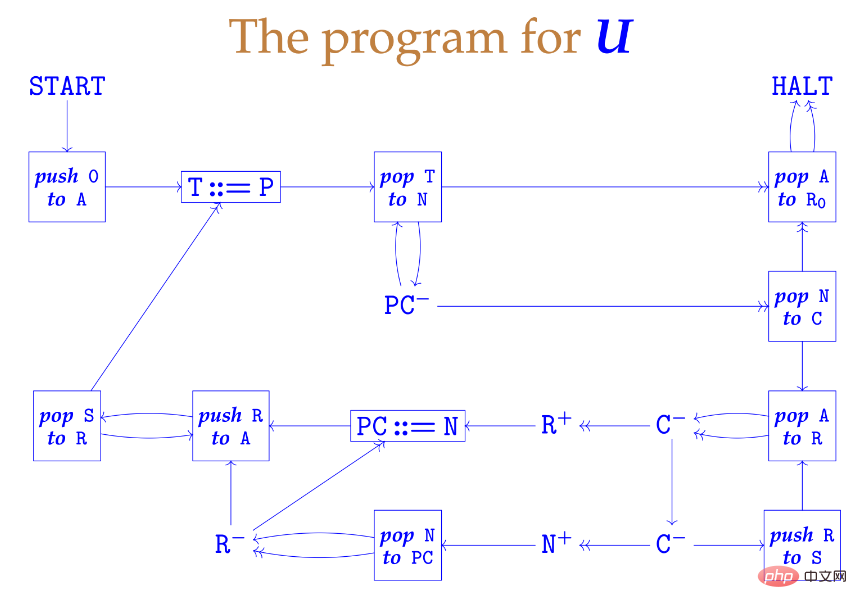
 3
3 を作成し、終了するかどうかを尋ねるプログラムを作成するだけです。 。ただし、停止の決定不可能性は厳密に表現され、証明されなければなりません。
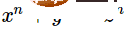
4 チューリングとモーリス・ウィルクス
5 チューリングとプリンストンの教会

6 教会とチューリングの説は正しいでしょうか?
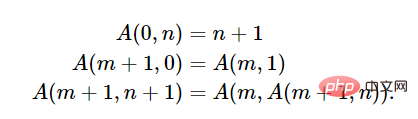
以上がチューリングマシン: コンピューターが存在しない状況で、どうやってコンピューティングについて語ることができるでしょうか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

