ホームページ >テクノロジー周辺機器 >AI >初めて導入しました!因果推論を使用して部分的に観察可能な強化学習を行う
初めて導入しました!因果推論を使用して部分的に観察可能な強化学習を行う
- WBOY転載
- 2023-04-15 11:07:021072ブラウズ
この記事「履歴ベースの強化学習のための高速反事実推論」では、因果推論の計算複雑さをオンライン強化学習と組み合わせられるレベルまで大幅に軽減する高速因果推論アルゴリズムを提案します。
この記事の理論的貢献は主に 2 つのポイントです:
1. 時間平均因果効果の概念を提案しました。
2. 有名なバックドア基準を単変量介入効果推定から多変量介入効果推定に拡張し、ステップ バックドア基準と呼びます。
背景
部分観察可能な強化学習と因果推論に関する基本的な知識が必要です。ここではあまり多くは紹介しませんが、いくつかのポータルを紹介します:
部分的に観察可能な強化学習:
POMDP の説明 https:/ / www.zhihu.com/zvideo/1326278888684187648
因果推論:
ディープ ニューラル ネットワークにおける因果推論 https://zhuanlan.zhihu .com/p/425331915
モチベーション
履歴情報からの特徴の抽出/エンコードは、部分的に観察可能な強化学習を解決するための基本的な手段です。主流の手法は、シーケンスツーシーケンス (seq2seq) モデルを使用して履歴をエンコードすることであり、たとえば、この分野で人気のある LSTM/GRU/NTM/Transformer 強化学習手法がこれに分類されます。このタイプの方法に共通するのは、履歴が履歴情報と学習シグナル (環境報酬) の間の相関関係に基づいてエンコードされることです。つまり、ある履歴情報の相関関係が大きいほど、それに割り当てられる重みが高くなります。 。
ただし、これらの方法では、サンプリングによって生じる交絡相関 を排除することはできません。以下の図に示すように、ドアを開けるために鍵を拾う例を示します。
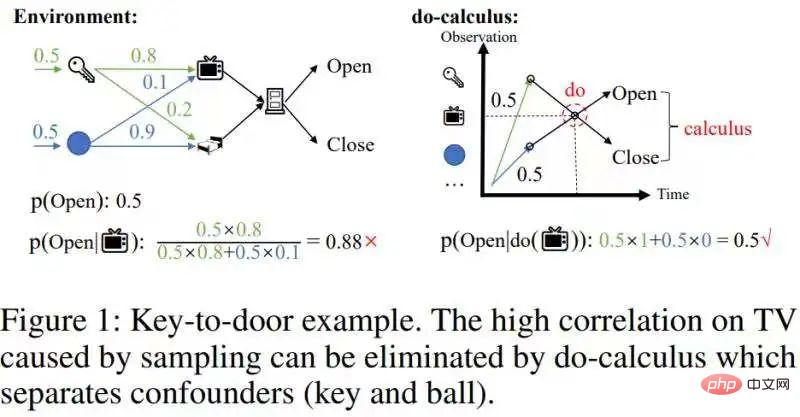
この交絡的な相関関係を除去する必要があります。
この交絡的な相関関係は、因果推論における計算計算によって取り除くことができます [1]:分離 潜在的に混乱を招く バックドア変数キーとボール、したがって、バックドア変数 (キー/ボール) と TV の間の統計的相関を遮断し、バックドア変数 (キー/ ball) Ball)Integrate (図 1 の右図)、実際の効果 p(Open|do( ))=0.5 が得られます。因果関係のある歴史的状態は比較的希薄であるため、交絡相関を除去すると、歴史的状態の規模を大幅に縮小できます。 したがって、因果推論を使用して履歴サンプルの交絡相関を除去し、次に seq2seq を使用して履歴をエンコードして、よりコンパクトな履歴表現を取得したいと考えています。
(この記事の動機)[1] 注: ここで考慮されているのは、人気のある科学リンク https:/ を使用してバックドアを使用して調整された計算です。 /blog.csdn .net/qq_31063727/article/details/118672598
難易度
歴史的シーケンスにおける因果推論の実行は、一般的な因果推論の問題とは異なります。履歴シーケンスの 変数は、時間次元と空間次元 の両方を持ちます。つまり、観測時間の組み合わせ 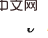 です。ここで、o は観測値、t はタイムスタンプです (対照的に、 MDP 非常に友好的で、マルコフ状態には空間次元しかありません)。 2 つの次元の重複により、履歴観測のスケールが非常に大きくなります。
です。ここで、o は観測値、t はタイムスタンプです (対照的に、 MDP 非常に友好的で、マルコフ状態には空間次元しかありません)。 2 つの次元の重複により、履歴観測のスケールが非常に大きくなります。 は各タイムスタンプでの観測値の数を表すために使用され、T は全長を表すために使用されます。値には
は各タイムスタンプでの観測値の数を表すために使用され、T は全長を表すために使用されます。値には  種類があります (正規形式の O() は複雑さの記号です)。 [2]
種類があります (正規形式の O() は複雑さの記号です)。 [2]
以前の因果推論手法は、単変量介入検出に基づいており、一度に 1 つの変数しか実行できませんでした。大規模な歴史的状態に対して因果推論を実行すると、非常に高い時間計算量が発生し、オンライン RL アルゴリズムと組み合わせることが困難になります。
#[2] 注: 単変量介入の因果効果の正式な定義は次のとおりです
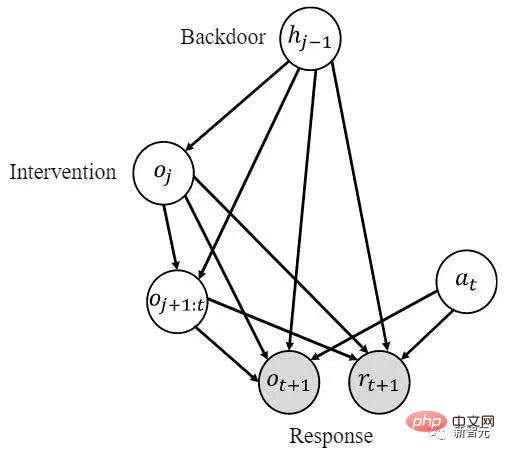
を考慮して、転送された変数に対する の因果関係を推定する必要があることを示します。 では、次の 2 つのステップを実行します。 1) 履歴状態に介入して を実行し、2) 以前の履歴状態を使用します はバックドア変数、 は応答変数です。次の積分を計算して、必要な因果効果 を取得します。

アイデア
この記事の核となる観察 (仮説) は、因果関係の状態は空間次元では疎であるということです。この観察は自然かつ一般的なものです。たとえば、鍵を使ってドアを開けると、その過程で多くの状態が観察されますが、鍵の観察値によってドアを開けることができるかどうかが決まります。この観察値はスパースを説明します。すべての観測値に対する割合。この疎性を利用して、多変数介入を通じて因果関係のない多数の歴史的状態を一度にフィルタリングすることができます。 しかし、因果関係は時間次元では希薄ではありません。ドアを開けるために鍵が使用される場合も同様です。鍵はほとんどの場合、エージェントによって監視されます。時間次元における因果効果の密度により、多変量介入を行うことができなくなります。因果効果なしに多数の歴史的状態を一度に除去することは不可能です。 上記の 2 つの観察に基づいて、私たちの中心的なアイデアは、
最初に空間次元で推論を行い、次に時間次元で推論を行うことです。空間次元の疎性を利用して、介入の数を大幅に削減します。 空間因果効果を個別に推定するために、最初に時間平均因果効果を取得することを提案します。これは、複数の歴史的状態の因果効果を時間の経過とともに平均することを意味します(具体的な定義については原文を参照)。 この考えに基づいて、私たちは問題に焦点を当てます。解決すべき中心的な問題は、どのように計算するかです。複数の 異なるタイム ステップ 同じ値を持つ変数に介入する方法です。 ( バックドア基準を改良し、多変量共同介入効果の推定値を推定するのに適した基準を提案します。任意の 2 つの介入変数 ステップバックドア調整式 ##この基準は、変数間の他の変数を分離します。 2 つの隣接するタイム ステップの値。これらはステップ バックドア変数と呼ばれます。この基準を満たす因果関係図では、介在する 2 つの変数の結合因果効果を推定できます。これには 2 つのステップが含まれます: ステップ 1. タイム ステップで i より小さい変数をバックドア変数として使用して、do 上記の式では、さらに多くのステップが使用されます。一般変数インジケータ X 。 3 つ以上の変数の場合、ステッピング バックドア基準を継続的に使用することで、2 つのタイム ステップごとに隣接する介在変数間の変数がステッピング バックドア変数とみなされ、継続的に計算されます。上の式から、多変数介入の共同因果効果
# で推定できます。 部分観測可能な強化学習問題に特有の、上の式の x を観測値 o に置き換えると、次のような因果効果の計算式が得られます: 定理 2。 この時点で、論文は空間因果効果 (つまり、時間平均因果効果) を計算するための式を示しています。この方法により、介入の数が O( #アルゴリズムの構造図は次のとおりです。 限界: 空間次元における因果推論は、すでに歴史的スケールを十分に圧縮しています。時間次元での因果推論は歴史スケールをさらに圧縮できますが、計算の複雑さのバランスをとる必要があることを考慮して、この記事では時間次元での相関推論を維持します (空間的因果効果のある歴史的状態に対して LSTM をエンドツーエンドで使用)。因果推論は使用しません。 検証
#将来の拡張に向けて考えられる方向性 #1. HCI は強化学習の種類に限定されません。この記事ではオンライン RL について研究していますが、HCI はオフライン RL やモデルベース RL などにも当然拡張でき、HCI を模倣学習に適用することも検討できます; 2. HCI は特別なハード アテンション メソッドとみなすことができます。因果効果のあるシーケンス ポイントは 1 のアテンション ウェイトを受け取り、それ以外の場合は 0 のアテンション ウェイトを受け取ります。この観点から、いくつかの配列予測問題も HCI を使用して処理しようとする可能性があります。  の 共同因果効果 に注意してください)。これは、バックドア基準は、複数の履歴変数の共同介入には適用されないためです。以下の図に示すように、二重変数
の 共同因果効果 に注意してください)。これは、バックドア基準は、複数の履歴変数の共同介入には適用されないためです。以下の図に示すように、二重変数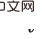 との共同介入を検討してください。
との共同介入を検討してください。  では、
では、 の後のタイム ステップにおけるバックドア変数の一部に
の後のタイム ステップにおけるバックドア変数の一部に  が含まれており、それらの間に共通のバックドア変数が存在しないことがわかります。二つ。
が含まれており、それらの間に共通のバックドア変数が存在しないことがわかります。二つ。 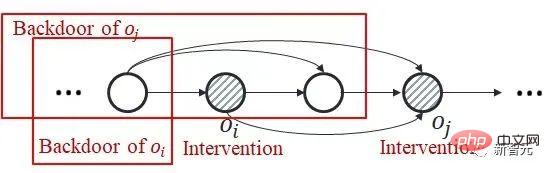
方法
 および
および  (i
(i
 因果効果 を推定します; ステップ 2. 決定された を取得します。
因果効果 を推定します; ステップ 2. 決定された を取得します。  バックドア変数と指定された
バックドア変数と指定された  が条件として使用され、
が条件として使用され、 と
と  の間の変数は次のようになります。
の間の変数は次のようになります。  に関する新しいバックドア変数 (つまり、
に関する新しいバックドア変数 (つまり、 および
および  に関するステップ バックドア変数) は、 を行うと推定されます。
に関するステップ バックドア変数) は、 を行うと推定されます。  の 条件付き因果効果 。したがって、共同因果効果は、これら 2 つの部分の積分になります。以下の図に示すように、ステップバイステップのバックドア基準では、通常のバックドア基準の 2 つのステップが使用されます。
の 条件付き因果効果 。したがって、共同因果効果は、これら 2 つの部分の積分になります。以下の図に示すように、ステップバイステップのバックドア基準では、通常のバックドア基準の 2 つのステップが使用されます。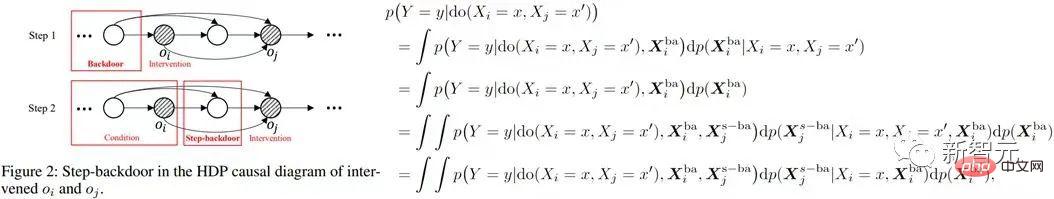
 は次のように得られます。
は次のように得られます。 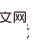 と
と 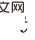 が与えられると、Do(o) の因果効果は
が与えられると、Do(o) の因果効果は 
 ) から O(
) から O(  )。次のステップは、空間的因果効果の希薄性 (この章の冒頭で述べた) を利用して、介入の数をさらに指数関数的に減らすことです。 1 つの観測値に対する介入を観測部分空間に対する介入に置き換えます。これは、スパース性を利用して計算を高速化する一般的なアイデアです (元の記事を参照)。この記事では、ツリーベースの履歴反事実推論 (T-HCI) と呼ばれる高速反事実推論アルゴリズムが開発されていますが、ここでは詳しく説明しません (詳細は原文を参照してください)。実際、多くの歴史的因果推論アルゴリズムはステッピング バックドア基準に基づいて開発でき、T-HCI はそのうちの 1 つにすぎません。最終結果は命題 3 (粗いから細かい CI) です。
)。次のステップは、空間的因果効果の希薄性 (この章の冒頭で述べた) を利用して、介入の数をさらに指数関数的に減らすことです。 1 つの観測値に対する介入を観測部分空間に対する介入に置き換えます。これは、スパース性を利用して計算を高速化する一般的なアイデアです (元の記事を参照)。この記事では、ツリーベースの履歴反事実推論 (T-HCI) と呼ばれる高速反事実推論アルゴリズムが開発されていますが、ここでは詳しく説明しません (詳細は原文を参照してください)。実際、多くの歴史的因果推論アルゴリズムはステッピング バックドア基準に基づいて開発でき、T-HCI はそのうちの 1 つにすぎません。最終結果は命題 3 (粗いから細かい CI) です。 の場合、粗いから細かい CI の介入数は
の場合、粗いから細かい CI の介入数は  # です。
# です。 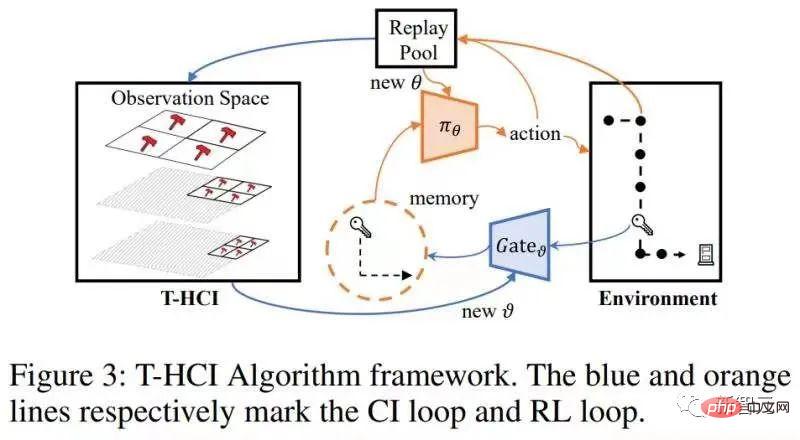
以上が初めて導入しました!因果推論を使用して部分的に観察可能な強化学習を行うの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

