ホームページ >テクノロジー周辺機器 >AI >ニューラル ネットワーク、多様体、トポロジーを直感的に理解するための 18 枚の図
ニューラル ネットワーク、多様体、トポロジーを直感的に理解するための 18 枚の図
- 王林転載
- 2023-04-12 19:58:041044ブラウズ
これまでのところ、ニューラル ネットワークに関する大きな懸念の 1 つは、ニューラル ネットワークが説明が難しいブラック ボックスであるということです。この記事では、主に、ニューラル ネットワークがパターン認識と分類に非常に効果的である理由を理論的に理解しています。その本質は、元の入力をアフィン変換と非線形変換の層を通じて、異なるカテゴリに簡単に区別できるようになるまで歪め、変形することです。実際、バックプロパゲーション アルゴリズム (BP) は、トレーニング データに基づいて歪み効果を継続的に微調整します。
約 10 年前から、ディープ ニューラル ネットワークはコンピューター ビジョンなどの分野で画期的な成果を上げ、大きな関心と注目を集めています。
しかし、まだ心配している人もいます。その理由の 1 つは、ニューラル ネットワークがブラック ボックスであるためです。ニューラル ネットワークが適切にトレーニングされていれば、高品質の結果が得られますが、それがどのように機能するかを理解するのは困難です。ニューラル ネットワークに障害が発生した場合、問題を特定することが困難になることがあります。
ディープ ニューラル ネットワーク全体を理解することは困難ですが、低次元のディープ ニューラル ネットワーク、つまり各層に数個のニューロンしか含まないネットワークから始めることができ、これは非常に理解しやすいです。視覚化手法を通じて、低次元ディープ ニューラル ネットワークの動作とトレーニングを理解できます。視覚化手法により、ニューラル ネットワークの動作をより直観的に理解し、ニューラル ネットワークとトポロジーの関係を観察できるようになります。
次に、特定のデータ セットを分類できるニューラル ネットワークの複雑さの下限など、多くの興味深いことについて説明します。
1. 簡単な例
非常に単純なデータセットから始めましょう。下の図では、平面上の 2 つの曲線が無数の点で構成されています。ニューラル ネットワークは、これらの点がどの線に属しているかを識別しようとします。
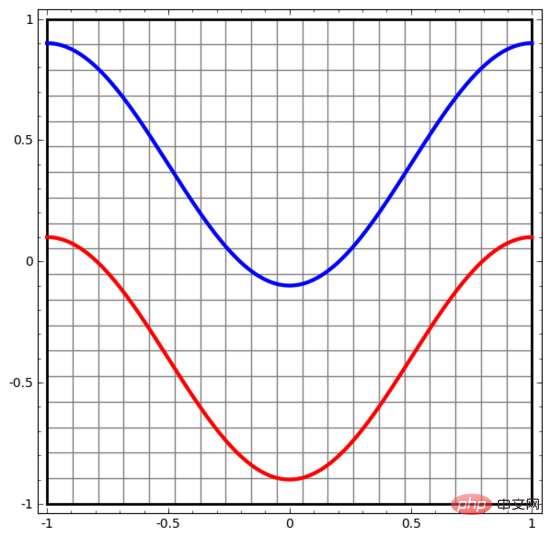
ニューラル ネットワーク (または分類アルゴリズム) の動作を観察する最も簡単な方法は、各データ ポイントがどのように分類されるかを確認することです。
入力層と出力層が 1 つだけある最も単純なニューラル ネットワークから始めます。このようなニューラル ネットワークは、2 種類のデータ ポイントを直線で単純に分離します。
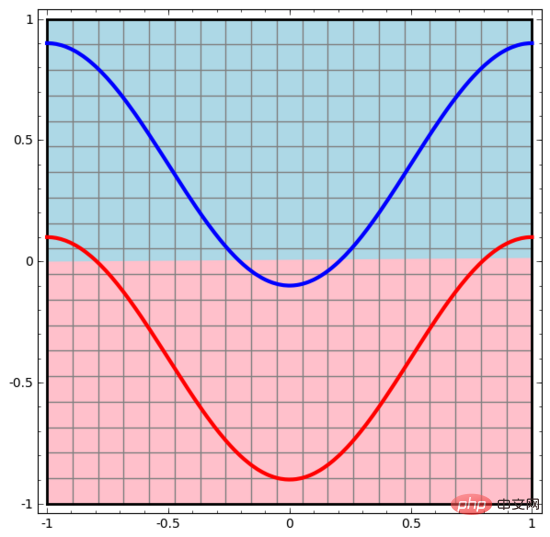
このようなニューラル ネットワークは単純すぎて粗雑です。最新のニューラル ネットワークには、入力層と出力層の間に隠れ層と呼ばれる複数の層があることがよくあります。最も単純な最新のニューラル ネットワークでも、少なくとも 1 つの隠れ層があります。
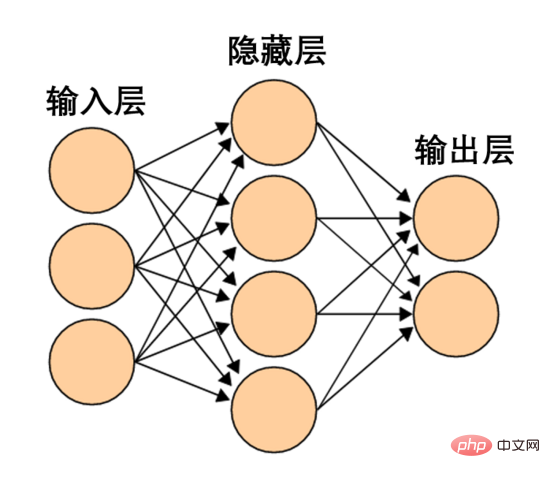
単純なニューラル ネットワーク、画像ソース Wikipedia
同様に、各データ ポイントに対してニューラル ネットワークが何を行うかを観察します。見てわかるように、このニューラル ネットワークはデータ ポイントを分離するために直線の代わりに曲線を使用します。明らかに、曲線は直線よりも複雑です。
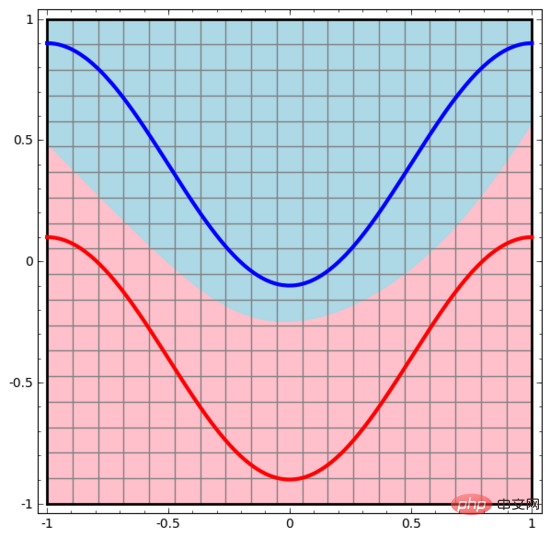
# ニューラル ネットワークの各層は、新しい表現を使用してデータを表します。データがどのように新しい表現に変換され、ニューラル ネットワークがデータをどのように分類するかを観察できます。表現の最後の層では、ニューラル ネットワークは 2 種類のデータ (高次元の場合は超平面) の間に線を描きます。
前の視覚化では、データの元の表現を見ました。これは、「入力層」でのデータの外観と考えることができます。次に、データが変換された後にどのように見えるかを見てみましょう。これは、データが「非表示レイヤー」でどのように見えるかとして考えることができます。
データの各次元は、ニューラル ネットワーク層のニューロンの活性化に対応します。
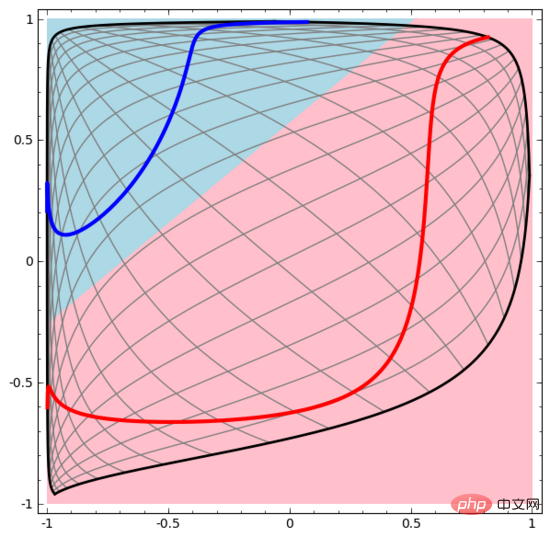
- 線形変換には「重み」行列 W を使用します
- 変換にはベクトル b を使用します
- tanh を使用してポイントごとに表現します
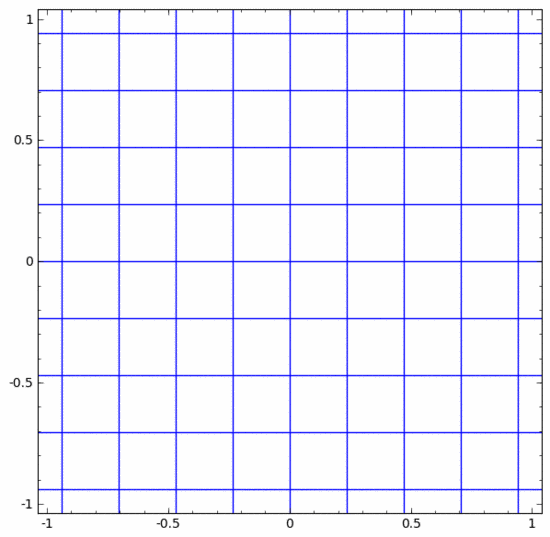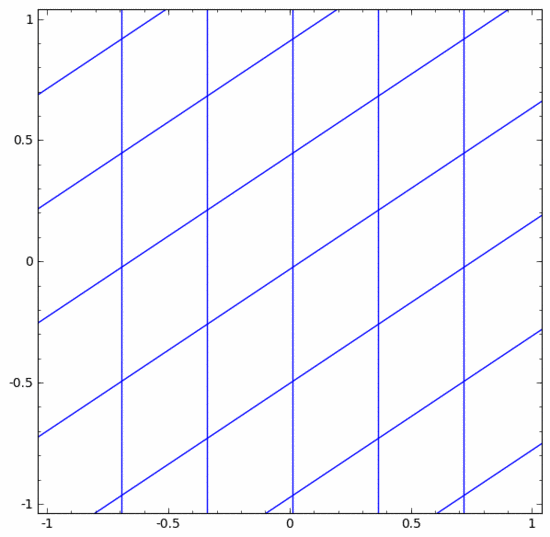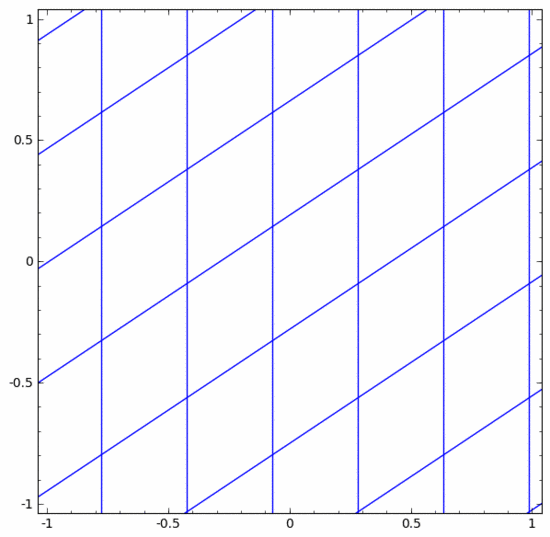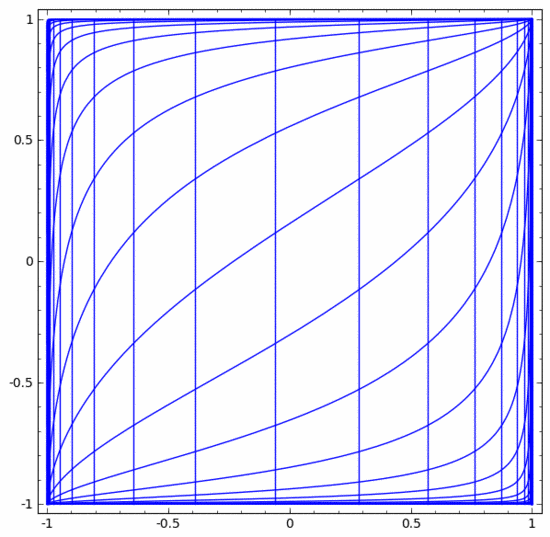
他の標準レイヤーでも状況はほぼ同じで、アフィン変換と単調活性化関数の点単位の適用で構成されます。
この方法を使用すると、より複雑なニューラル ネットワークを理解できます。たとえば、以下のニューラル ネットワークは 4 つの隠れ層を使用して、わずかに絡み合った 2 つのスパイラルを分類します。データを分類するために、データの表現が継続的に変換されることがわかります。 2 つの螺旋は最初は絡み合っていますが、最終的には直線で分離できます (線形分離可能)。
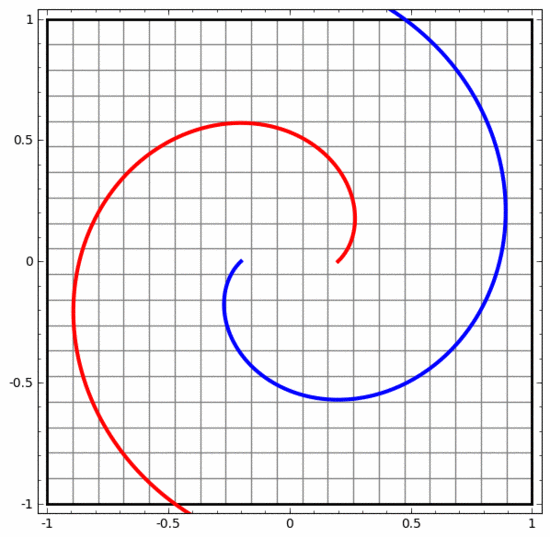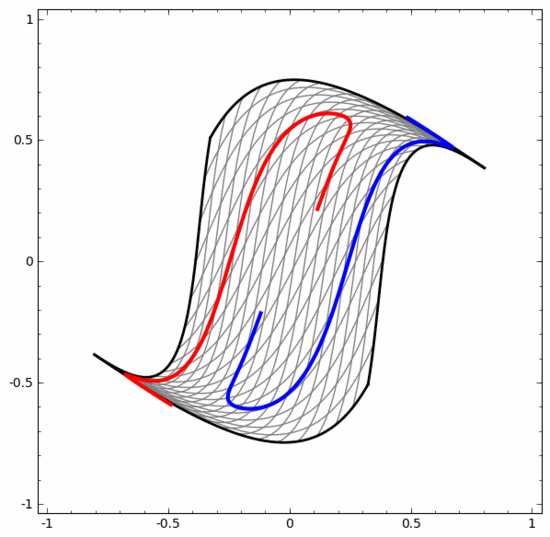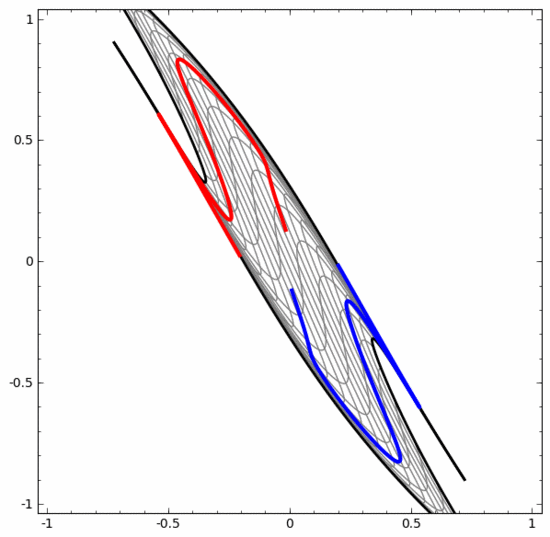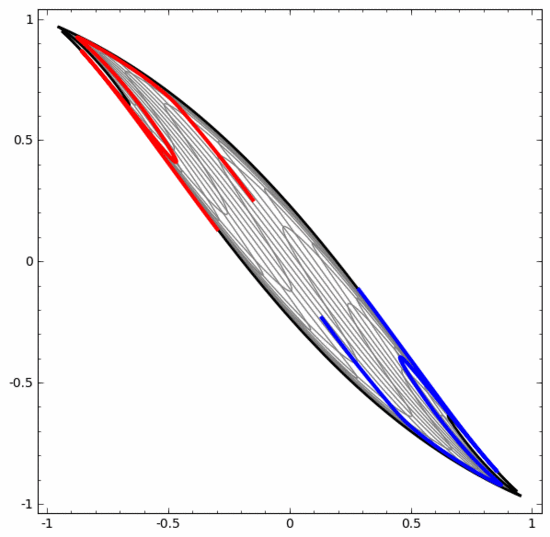
一方、以下のニューラル ネットワークも複数の隠れ層を使用していますが、より深く絡み合った 2 つのスパイラルを分割できません。
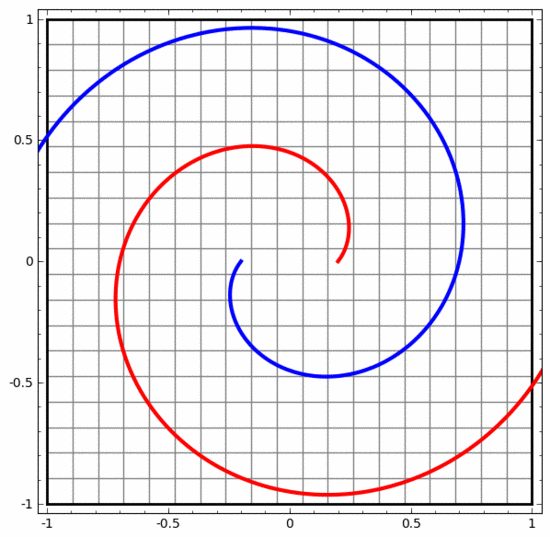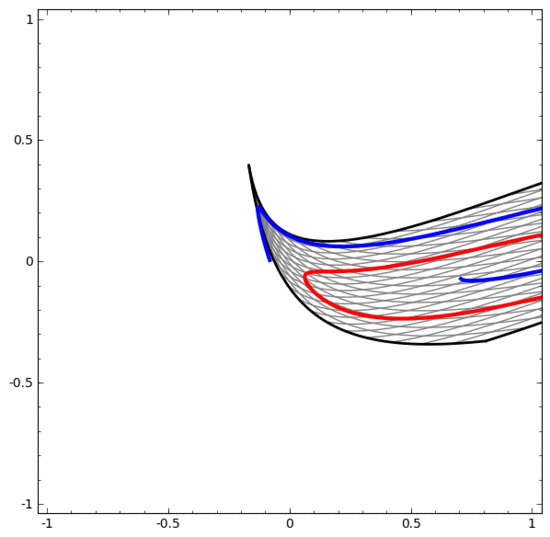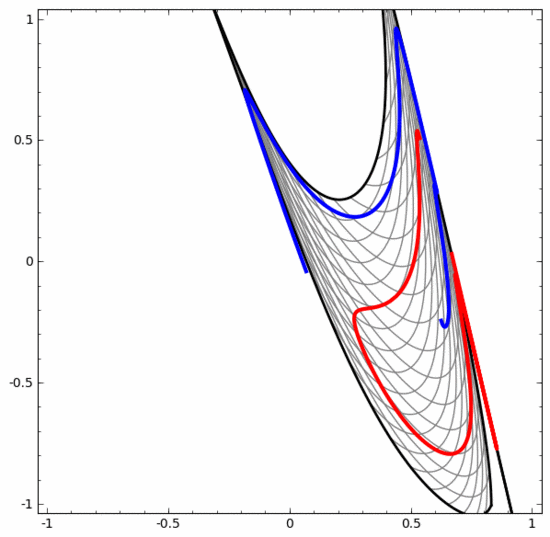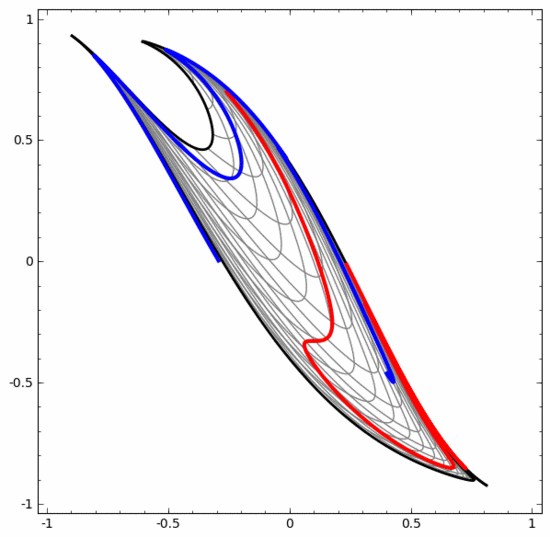
現時点では低次元ニューラル ネットワークのみを使用しているため、上記 2 つのスパイラル分類タスクにはいくつかの課題があることを明確に指摘する必要があります。もっと広範なニューラルネットワークを使用すれば、すべてがはるかに簡単になるでしょう。
(Andrej Karpathy は ConvnetJS に基づいた優れたデモを作成しました。これにより、人々はこの種の視覚的なトレーニングを通じてニューラル ネットワークを対話的に探索できるようになります。)
3. Tanh 層のトポロジ
ニューラル ネットワークの各層は空間を引き伸ばしたり圧縮したりしますが、空間を剪断したり、分割したり、折りたたんだりすることはありません。直観的には、ニューラル ネットワークはデータのトポロジー特性を破壊しません。たとえば、データのセットが連続的である場合、その変換された表現も連続的になります (逆も同様です)。
このような位相特性に影響を与えない変換は、同相同相写像と呼ばれます。形式的には、これらは双方向連続関数の全単射です。
定理: 重み行列 W が非特異で、ニューラル ネットワークの層に N 個の入力と N 個の出力がある場合、この層のマッピングは同相的です (特定のドメインと値の範囲に対して)。
証明: 段階的にやってみましょう:
1. W にゼロ以外の行列式があると仮定します。この場合、それは線形逆関数を伴う双一次一次関数になります。線形関数は連続です。次に、「W を掛ける」などの変換は同相同型です;
2. 「平行移動」変換は同相同型です;
3. Tanh (シグモイドとソフトプラスもありますが、 ReLU はありません)は連続逆関数をもつ連続関数です。 (特定のドメインと範囲の場合)、それらは全単射であり、それらの点ごとの適用は同相同型です。
したがって、W がゼロ以外の行列式を持つ場合、このニューラル ネットワーク層は同相的になります。
このようなレイヤーをランダムに組み合わせても、この結果は依然として当てはまります。
4. トポロジと分類
2 種類のデータ A と B を含む 2 次元データ セットを見てみましょう:
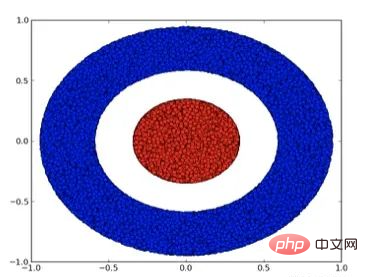
A は赤、B は青
説明: このデータ セットを分類するには、ニューラル ネットワーク (深さに関係なく) に 3 つ以上の層を含む隠れユニットが必要です。 。
前に述べたように、分類にシグモイド ユニットまたはソフトマックス層を使用することは、最後の層の表現で超平面 (この場合は直線) を見つけて A と B を分離することと同じです。隠れユニットが 2 つしかないため、ニューラル ネットワークはトポロジー的にこの方法でデータを分離することができないため、上記のデータセットを分類できません。
以下のビジュアライゼーションでは、隠れ層が直線を分割線として使用してデータの表現を変換します。分割線は回転移動を続けますが、2 種類のデータ A と B をうまく分離することはできません。
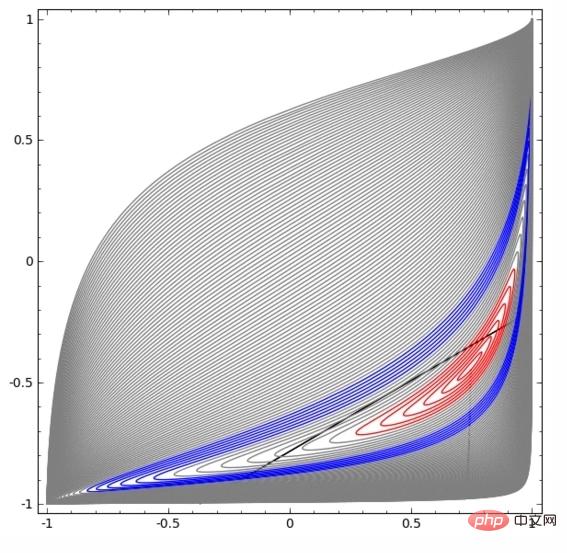
ニューラル ネットワークがどれほどよく訓練されていても、分類タスクを適切に完了することはできません
最終的には、かろうじて極小値を達成することしかできません。 、分類精度は 80% に達します。
上記の例には隠れ層が 1 つしかなく、隠れユニットが 2 つしかないため、いずれにしても分類に失敗します。
証明: 隠れユニットが 2 つしかない場合、この層の変換は同型であるか、層の重み行列の行列式が 0 です。同型写像であれば、A は B に囲まれたままであり、A と B を直線で分けることはできません。行列式が 0 の場合、データ セットはある軸で折りたたまれます。 A は B に囲まれているため、任意の軸で A を折りたたむと、A データ ポイントの一部が B と混合され、A と B を区別できなくなります。
しかし、3 番目の隠しユニットを追加すると、問題は解決されます。このとき、ニューラル ネットワークはデータを次の表現に変換できます。
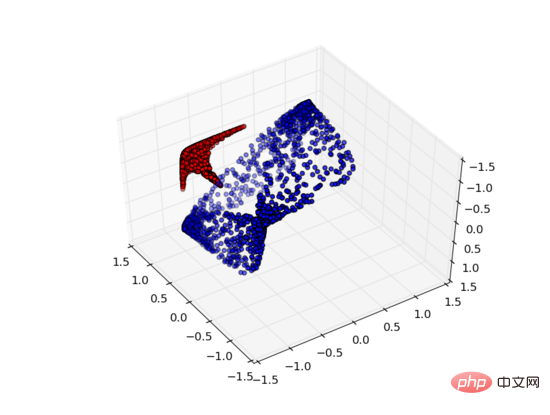
#このとき、超平面を使用して A と B を分離できます。
その原理をよりよく説明するために、より単純な 1 次元のデータ セットを例として示します。
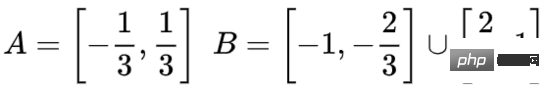
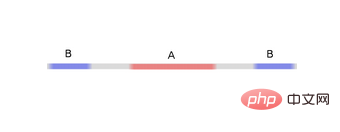
の場合はどちらかの隠しユニットが発動し、
の場合はもう一方の隠しユニットが発動します。前の隠しユニットが発動し、次の隠しユニットが発動していない場合、Aに属するデータ点であると判断できます。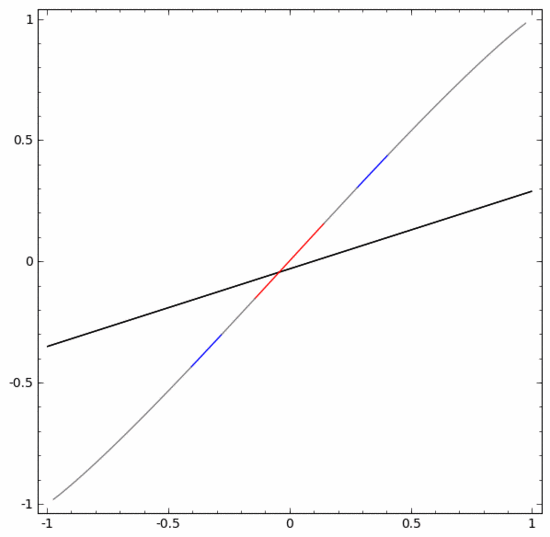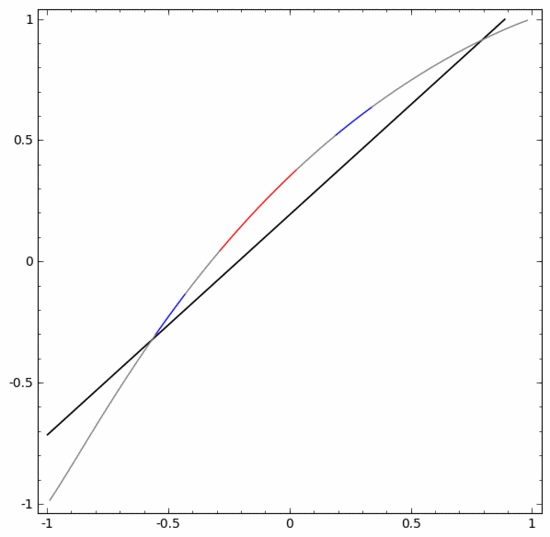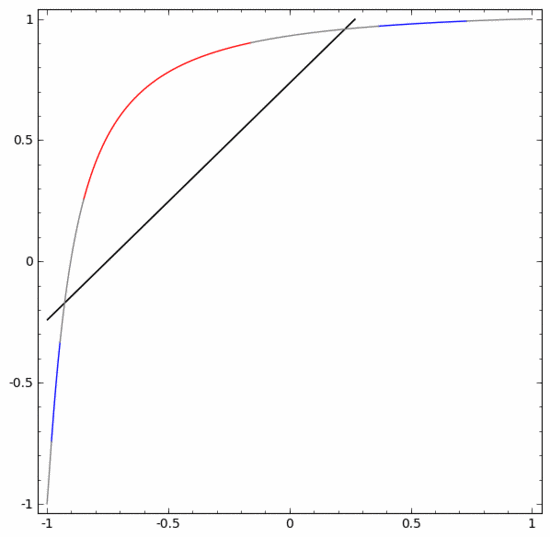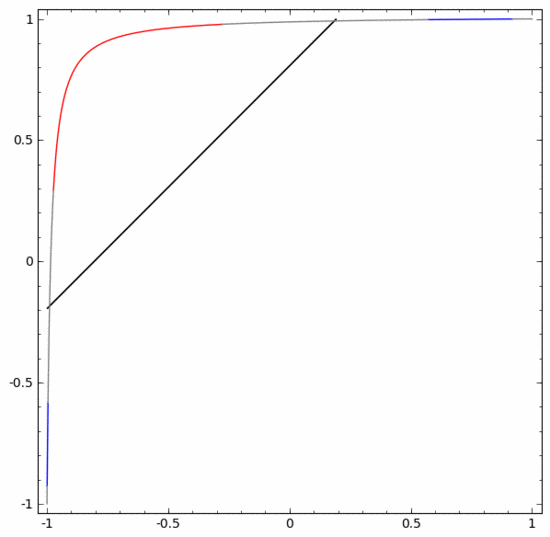
5. 多様体仮説
多様体仮説は、現実世界のデータセット (画像データなど) を処理するのに意味がありますか?それは理にかなっていると思います。 
多様体仮説は、自然データがその埋め込み空間内で低次元多様体を形成することを意味します。この仮説には理論的および実験的な裏付けがあります。多様体仮説を信じる場合、分類アルゴリズムのタスクは、結局のところ、もつれた多様体のセットを分離することになります。
前の例では、1 つのクラスが別のクラスを完全に囲んでいました。ただし、現実世界のデータでは、犬の画像多様体が猫の画像多様体に完全に囲まれる可能性は低いです。ただし、次のセクションで説明するように、他のより合理的なトポロジー状況では依然として問題が発生する可能性があります。
6. リンクとホモトピー
次に、別の興味深いデータセット、相互にリンクされた 2 つのトーラス (トーラス) A と B について説明します。
前に説明したデータ セットの状況と同様に、n 1 次元を使用せずに n 次元のデータ セットを分離することはできません (この場合、n 1 次元はは 4 次元です)。 リンク問題は、トポロジーにおける結び目理論に属します。リンクを見たときに、それが壊れたリンクであるかどうかをすぐに判断できない場合があります（リンクが解除されるとは、互いに絡み合っているものの、継続的な変形によって分離できることを意味します）。
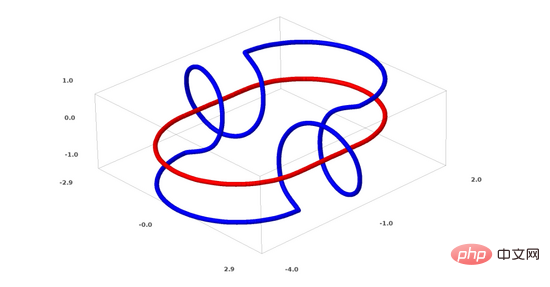ノット理論の観点から見ると、ニューラル ネットワークによって生成されたデータ表現の継続的な視覚化は、優れたアニメーションであるだけでなく、リンクを解くプロセスでもあります。トポロジでは、これを元のリンクと分離されたリンクの間の周囲同位体と呼びます。
多様体 A と多様体 B の間の周囲の同型写像は連続関数です:
それぞれは X の同型写像です。は特性関数であり、A を B にマッピングします。つまり、A からそれ自体へのマッピングから A から B へのマッピングに常に移行します。定理: 次の 3 つの条件が同時に満たされる場合: (1) W が特異でない; (2) 隠れ層のニューロンの順序は手動で配置できる; (3) 隠れユニットの数が 1 より大きい場合、ニューラル ネットワークの入力 ニューラル ネットワーク層によって生成される表現間にはラップアラウンド類似性があります。
証明: ステップバイステップで進めます:
1. 最も難しい部分は線形変換です。線形変換を達成するには、W に正の行列式が必要です。私たちの前提は、行列式が非ゼロであり、行列式が負の場合、2 つの隠れたニューロンを交換することで行列式を正に変えることができるということです。正の行列式の空間は経路接続されているので、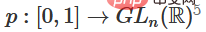
があり、したがって 
, 
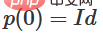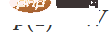となります。関数 
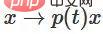を使用すると、時間 t の各点で x に連続遷移の行列を乗算して、固有関数を W 変換に連続的に遷移させることができます。
2. 関数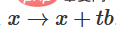 
を介して、特性関数から b 翻訳に移行できます。
3. 関数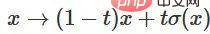 
を通じて、特性関数からポイントバイポイント アプリケーションに移行できます。
次の質問に興味がある人もいると思います。そのような周囲同位体を自動的に発見でき、また、いくつかの異なるリンクの等価性や特定のリンクの分離性も自動的に証明できるプログラムは開発できますか。また、この点でニューラル ネットワークが現在の SOTA テクノロジーに勝てるかどうかも知りたいと思っています。
今話しているリンクの形式は現実世界のデータにはおそらく現れませんが、現実世界のデータには高次元の一般化が存在する可能性があります。
リンクとノットはどちらも 1 次元多様体ですが、それらを分離するには 4 次元が必要です。同様に、n 次元多様体を分離するには、より高次元の空間が必要です。すべての n 次元多様体は 2n 2 次元で分離できます。
7. 簡単な方法
ニューラル ネットワークの場合、最も簡単な方法は、絡み合った多様体を直接引き離し、絡み合った部分を取り出すことです。これは私たちが追求している根本的な解決策ではありませんが、比較的高い分類精度を達成し、比較的理想的な極小値を達成できます。
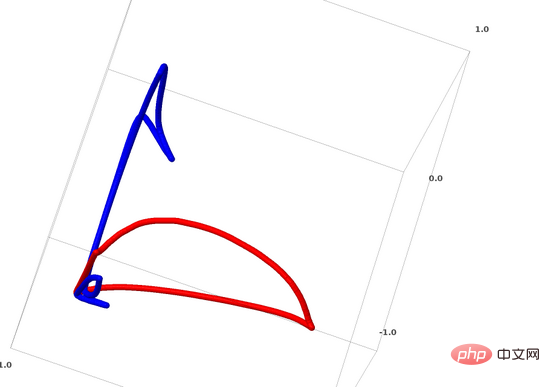
このアプローチでは、ストレッチしようとしている領域で非常に高い導関数が得られます。これに対処するには、データ ポイントのレイヤーの導関数にペナルティを与える収縮ペナルティを使用する必要があります。
極小値はトポロジカル問題の解決には役に立ちませんが、トポロジカル問題は上記の問題を調査して解決するための良いアイデアを提供する可能性があります。
一方、良好な分類結果を得ることのみを気にする場合、多様体の小さな部分が別の多様体と絡み合っている場合は問題になるでしょうか?分類結果だけを気にするのであれば、これは問題ないようです。
(私の直感では、このような近道をするのはよくなく、簡単に行き止まりにつながる可能性があります。特に、最適化問題では、極小値を求めることは実際には問題を解決しません。A を選択した場合、問題を真に解決できないソリューションは、最終的に良好なパフォーマンスを達成できなくなります。)
8.多様体の操作により適したニューラル ネットワーク層を選択しますか?
標準のニューラル ネットワーク層は、アフィン変換と点単位の活性化関数を使用するため、多様体の操作には適していないと思います。
おそらくまったく異なるニューラル ネットワーク層を使用できるでしょうか?
思いつくアイデアの 1 つは、まず、多様体を動かしたい方向を方向とするベクトル場をニューラル ネットワークに学習させることです。
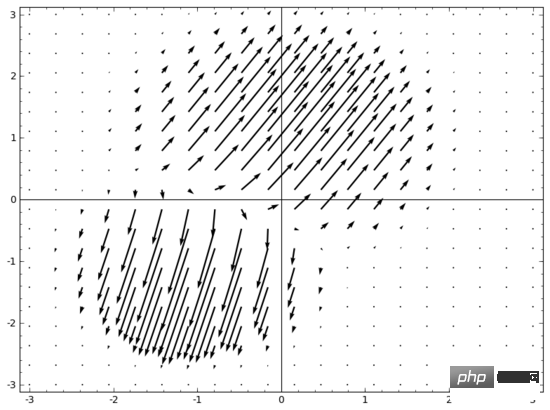
次に、これに基づいて空間を変形します。
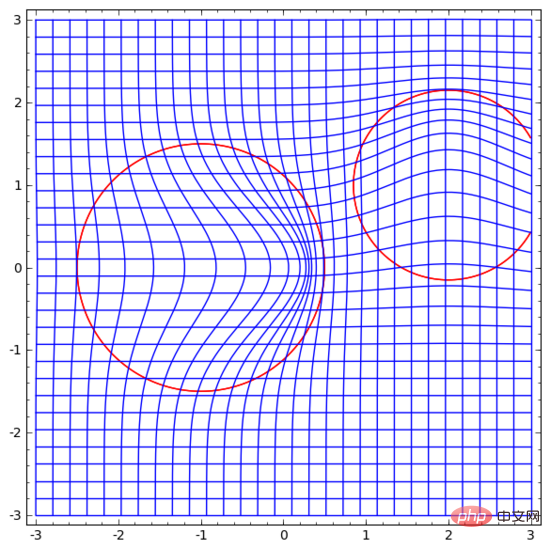
固定点でベクトル場を学習し (トレーニング セットからいくつかの固定点をアンカーとして選択するだけです)、いくつかの点で補間できます。方法。上記のベクトル場の形式は次のとおりです。
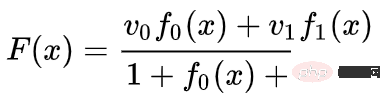
ここで、 と はベクトル、 と は n 次元のガウス関数です。このアイデアは動径基底関数からインスピレーションを得ています。
9. K 最近傍層
私のもう 1 つの観点は、線形分離性はニューラル ネットワークにとって過剰かつ不合理な要件である可能性があり、おそらく k 最近傍 (k-NN) を使用すると、もっと良くなってください。ただし、k-NN アルゴリズムはデータの表現に大きく依存しているため、k-NN アルゴリズムで良好な結果を得るには、適切なデータ表現が必要です。
最初の実験では、いくつかの MNIST ニューラル ネットワーク (2 層 CNN、ドロップアウトなし) を 1% 未満のエラー率でトレーニングしました。次に、最後のソフトマックス層を破棄して k-NN アルゴリズムを使用したところ、エラー率が 0.1 ～ 0.2% 減少することが複数回の結果で示されました。
しかし、このアプローチはまだ間違っていると感じています。ニューラル ネットワークは依然として線形分類を試みていますが、k-NN アルゴリズムを使用しているため、発生するエラーの一部をわずかに修正することができ、それによってエラー率が減少します。
(1/距離) 重み付けにより、k-NN は作用するデータ表現に対して微分可能です。したがって、k-NN 分類のためにニューラル ネットワークを直接トレーニングできます。これは、ソフトマックス レイヤーと同様に機能する「最近傍」レイヤーと考えることができます。
計算コストが高すぎるため、各ミニバッチのトレーニング セット全体をフィードバックすることは望ましくありません。ミニバッチ内の他の要素のカテゴリに基づいてミニバッチ内の各要素を分類し、各要素に (1/(分類ターゲットからの距離)) の重みを与えるのが良いアプローチだと思います。
残念ながら、複雑なアーキテクチャであっても、k-NN アルゴリズムを使用してもエラー率は 4 ～ 5% までしか減少できませんが、単純なアーキテクチャを使用するとエラー率は高くなります。ただし、ハイパーパラメータにはあまり力を入れませんでした。
しかし、私は依然として k-NN アルゴリズムを気に入っています。なぜなら、k-NN アルゴリズムの方がニューラル ネットワークに適しているからです。私たちは、多様体を分離するために超平面を使用することに固執するのではなく、同じ多様体上の点を互いに近づけたいと考えています。これは、単一の多様体を縮小しながら、異なるカテゴリの多様体間のスペースを大きくすることに相当します。これにより問題が単純化されます。
10. 概要
データの特定のトポロジー特性により、(ニューラル ネットワークの深さに関係なく) 低次元ニューラル ネットワークを使用してこれらのデータを線形分離できない場合があります。スパイラルなど技術的に実現可能な場合でも、低次元ニューラル ネットワークでは分離を達成するのが非常に困難です。
データを正確に分類するために、ニューラル ネットワークではより広い層が必要になる場合があります。さらに、従来のニューラル ネットワーク層は多様体の操作には適しておらず、重みを手動で設定したとしても、理想的なデータ変換表現を得るのは困難です。新しいニューラル ネットワーク層、特に機械学習を多様な観点から理解することに触発された新しいニューラル ネットワーク層は、優れたサポート役割を果たすことができる可能性があります。
以上がニューラル ネットワーク、多様体、トポロジーを直感的に理解するための 18 枚の図の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。