ホームページ >テクノロジー周辺機器 >AI >グラフ埋め込みアルゴリズムに関する簡単な説明
グラフ埋め込みアルゴリズムに関する簡単な説明
- 王林転載
- 2023-04-12 17:52:062619ブラウズ

#パート 01
##● ##グラフ埋め込みとは ●
グラフの埋め込みは、グラフ構造データを低次元の密なベクトルにマッピングするプロセスです。同時に、元のグラフ内で類似した位相構造または近い属性を持つノードもベクトル内で近い位置に配置されます。グラフ構造のデータを機械学習アルゴリズムに効率的に入力することが難しいという問題を効果的に解決します。#グラフの表現と保存については、隣接行列を使用することが最も簡単に考えられます。グラフ内の各ノードに番号を付けて、
の行列を構築します。ここで、 はノードの数を表します。グラフ内の 2 つのノードがエッジで接続されているかどうかによって、隣接行列内の対応する位置の値が決まります。この表現方法は非常に理解しやすく直感的ですが、非常に非効率です。実際のシナリオでは、グラフには数千またはそれ以上のノードが含まれる可能性があり、ほとんどのノードはエッジで接続されていないため、結果として得られる隣接行列が非常にまばらになります。隣接行列を使用してグラフを表現および保存するには、高い計算コストとスペース コストが必要ですが、グラフ埋め込みアルゴリズムを使用すると、グラフ分析の問題を効率的に解決できます。
はノードの数を表します。グラフ内の 2 つのノードがエッジで接続されているかどうかによって、隣接行列内の対応する位置の値が決まります。この表現方法は非常に理解しやすく直感的ですが、非常に非効率です。実際のシナリオでは、グラフには数千またはそれ以上のノードが含まれる可能性があり、ほとんどのノードはエッジで接続されていないため、結果として得られる隣接行列が非常にまばらになります。隣接行列を使用してグラフを表現および保存するには、高い計算コストとスペース コストが必要ですが、グラフ埋め込みアルゴリズムを使用すると、グラフ分析の問題を効率的に解決できます。 
##●
基本概念 ● コンセプト 1 画像:
グラフは 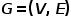 として表されます。
として表されます。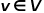 はノードを表します。
はノードを表します。 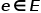 エッジを表します。
エッジを表します。 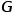 #ノード タイプ マッピング機能付き
#ノード タイプ マッピング機能付き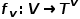 およびエッジ タイプ マッピング機能# #####関連する。
およびエッジ タイプ マッピング機能# #####関連する。 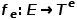 はノード タイプのコレクションを表し、
はノード タイプのコレクションを表し、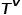 はエッジ タイプのコレクションを表します。
はエッジ タイプのコレクションを表します。 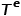 #コンセプト 2 同型グラフ:
#コンセプト 2 同型グラフ:
#グラフ
## #######、で###############。つまり、すべてのノードは 1 つのタイプに属し、すべてのエッジは 1 つのタイプに属します。たとえば、ソーシャル ネットワークのユーザー注目関係グラフには、ノード タイプ (ユーザー) とエッジ タイプ (注目関係) が 1 つだけあります。#コンセプト 3 異種グラフ: 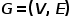 #グラフ
#グラフ 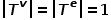 #、
#、
または
。つまり、複数のノード タイプまたはエッジ タイプが存在します。たとえば、学術ネットワークのグラフ構造には、論文、著者、会議などの複数のノード タイプが存在します。エッジ関係には、それらの間の創造的な関係が含まれます。著者と論文、論文と学会、それらの間の出版関係、論文間の引用関係など。 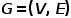 コンセプト 4 一次類似性:
コンセプト 4 一次類似性: 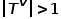
2 つのノードを接続するエッジの重みが大きいほど、それらの間の一次類似度は大きくなります。ノード 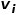 とノード
とノード 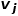 の間の一次類似度は ## と表されます。
の間の一次類似度は ## と表されます。 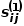 #、
#、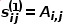 があります。
があります。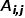 はノード ## です。
はノード ## です。 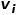 # とノード
# とノード 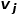 の間のエッジ
の間のエッジ  の重み。
の重み。
2 つのノードが隣接している場合ネットワーク 構造が類似しているほど、構造間の 2 次類似性が高くなります。ノード
# とノード #図 1 二次相似図 概念 6 図の埋め込み: 入力グラフと事前定義された埋め込み次元が与えられた場合、グラフの埋め込みとは、グラフのプロパティを可能な限り保持しながら、グラフを次元空間に変換することです。グラフを表すために次元ベクトルまたは ##パート 03 #グラフ埋め込みアルゴリズムの分類#● 過去数十年にわたり、研究者たちは多くの優れたアルゴリズムを提案しており、ソーシャル ネットワーク、通信ネットワーク、その他のシナリオに大きな効果があることが証明されています。業界では通常、出力粒度の違いに基づいて、これらのグラフ埋め込みアルゴリズムを次の 3 つのカテゴリに分類します。 # (1) ノード埋め込み ノードの埋め込みは、最も一般的なタイプです。グラフ内の各ノードは、低次元空間のベクトルによって表されます。「類似した」ノードの埋め込みベクトル表現も同様です。グラフ内のノードを分析し、ノードの分類やノードのクラスタリングなどのタスクを実行する必要がある場合、通常はノードの埋め込みが選択されます。 (2) エッジ埋め込み ベクトルを使用してグラフを低次元でマッピングするspace の各エッジが表現されます。エッジはノードのペアで構成され、通常はノードとペアの関係を表します。エッジの埋め込みは、グラフ内のエッジを分析し、ナレッジ グラフの関係予測やリンク予測などのタスクを実行する必要がある場合に適しています。 (3) グラフの埋め込み 低次元空間のベクトルを使用して埋め込みますA 表現全体は図、通常は分子やタンパク質などの小さな図によって表されます。グラフをベクトルとして表すと、異なるグラフ間の類似性の計算が容易になり、グラフの分類問題が解決されます。 異なるタスク要件により、選択されるグラフ埋め込みアルゴリズムが決まります。スペースの都合により、ここではノード埋め込みにおける DeepWalk アルゴリズムと Node2Vec アルゴリズムを抜粋して詳細な調査を比較します。 #パート 04 ##● クラシックなグラフ埋め込みアルゴリズム ● #1.DeepWalk アルゴリズム 自然言語処理の分野における word2vec のアイデアに触発され、Perozzi et al.ノード表現ベクトルのモデル化により、ノード間の共起関係をコーパス内の単語間の共起関係に類推し、DeepWalkアルゴリズムを提案する。グラフ内のノードの隣接ノードのシーケンスは、ノード コンテキストのコーパスに相当するランダム ウォークによって収集され、グラフ内のノード間の共起関係を抽出する問題を解決できます。ノード シーケンスの長さと開始点を事前に設定します。ランダム ウォーク戦略は、隣接ノードの中から次の歩行ノードを決定する方法を示します。この手順を繰り返して、条件を満たすシーケンスを取得します。ランダム ウォーク ダイアグラムを図に示します。 2. 表示します。 図 2 ランダム ウォークの概略図 word2vec アルゴリズムの単語は対応しますグラフ内のノード #ノードの潜在的な特徴表現をさらに学習するために、DeepWalk アルゴリズムにはマッピング関数が導入されています #図 3 に示すように、スキップグラム モデルには 2 つのキー行列が含まれており、1 つは中心単語ベクトル行列です。 、もう 1 つは背景単語ベクトル行列 #ランダム ウォーク プロセスでは、サンプリング シーケンス内のノード間の順序関係は考慮されません。これにより、より良い可能性があります。ノードの近接関係を効果的に反映し、計算コストを削減します。 #図 3 スキップグラム モデル図 2.Node2Vec アルゴリズム 研究者 Grover A と Leskovec J は、DeepWalk アルゴリズムに基づいて Node2Vec アルゴリズムを提案しました。 Node2Vec アルゴリズムは、DeepWalk アルゴリズムのランダム ウォークを通じてノード シーケンスを生成するプロセスを最適化し、パラメーター ここで、 はスレーブ ノードを表します。ノード 図 4 Node2Vec ランダム ウォーク戦略図 # Node2Vec のランダム ウォーク戦略は、図 4 に示すように 2 つのパラメーターに基づいて制御されます。エッジ からノード ## に移動するとき#ネクストホップ ノードを選択する必要がある場合、次の 3 つの状況が考えられます。 # を返す####。 (2) (3) つまり、パラメータ ##● #概要 ##● 情報技術の急速な発展に伴い、ネットワーク環境はますます複雑化し、ネットワーク攻撃が多発しており、その中でもAPT攻撃が多発しており、企業が求めるセキュリティ課題となっています。注意を払う。実際、APT 攻撃が発生する基本環境であるネットワーク自体は、コンピュータやその他の要素から構成されるネットワーク構造であり、これらの要素間の関係をグラフ データ構造で表現し、攻撃を変形させることを考えることは難しくありません。検出問題をグラフ内のノード、エッジ、またはサブグラフ分類タスクに組み込みます。グラフの埋め込みは、多くの研究余地がある豊富な問題です。モデルのトレーニング効率を向上させ、モデルの構築方法を革新し、グラフ埋め込みのアイデアをより多くの生産実践に適用する方法についてです。企業は、より良いソリューションを見つけるためにさらなる研究が必要です。回答。 参考文献 [1]Xu M. グラフ埋め込み手法とその応用について[J]. SIAM Review, 2021, 63(4): 825-853. [2]Cai H、Zheng V W、Chang K C C . 包括的なグラフ埋め込みの調査: 問題、技術、およびアプリケーション[J]. IEEE Transactions on Knowledge and Data Engineering, 2018, 30(9): 1616-1637. ##[3]Goyal P、Ferrara E. グラフ埋め込み技術、アプリケーション、およびパフォーマンス: 調査[J]. Knowledge-Based Systems, 2018, 151: 78-94. #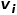
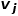 # # の間の 2 次類似度# は、
# # の間の 2 次類似度# は、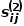
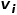 と
と 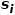 # の近隣です。 ## の近隣地域
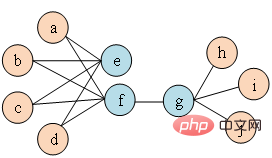
# の近隣です。 ## の近隣地域 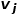 間の類似性。図 1 に示すように、ノード f とノード g を接続するエッジがあるため、ノード f とノード g は一次相似になります。ノード e とノード g を接続するエッジはありませんが、ノード e とノード g には 4 つの同一の隣接ノードがあるため、ノード e とノード g は二次的に類似します。
間の類似性。図 1 に示すように、ノード f とノード g を接続するエッジがあるため、ノード f とノード g は一次相似になります。ノード e とノード g を接続するエッジはありませんが、ノード e とノード g には 4 つの同一の隣接ノードがあるため、ノード e とノード g は二次的に類似します。 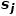
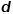 次元ベクトルのセットを使用して、一次類似度または高次類似度に基づいてグラフ属性の保存度を定量化します。 、各ベクトルはノードやエッジなどのグラフの一部の埋め込みを表します。
次元ベクトルのセットを使用して、一次類似度または高次類似度に基づいてグラフ属性の保存度を定量化します。 、各ベクトルはノードやエッジなどのグラフの一部の埋め込みを表します。 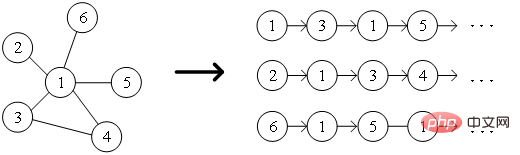
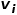 # に、単語列はランダム ウォークによって得られたノード列に対応し、ランダム ウォーク
# に、単語列はランダム ウォークによって得られたノード列に対応し、ランダム ウォーク 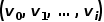 # では、式に示すように最適化目的関数を定義します。
# では、式に示すように最適化目的関数を定義します。 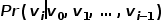
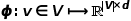 、グラフ内のノードの
、グラフ内のノードの 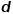 # 次元ベクトルへのマッピングを実現するには、問題は可能性の推定に変換されます。次の式の。
# 次元ベクトルへのマッピングを実現するには、問題は可能性の推定に変換されます。次の式の。 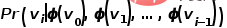
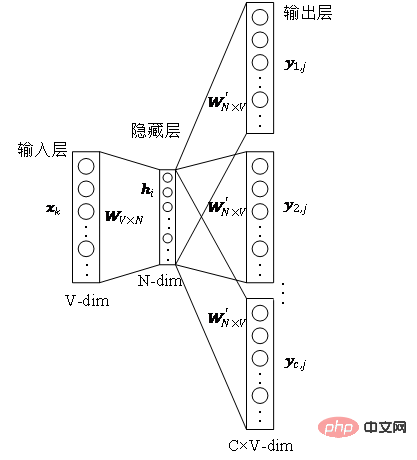
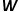 これら 2 つの重み行列はそれぞれ、単語が異なる役割を果たすときに単語に関連付けられた単語ベクトルを表します。 。 Skip-gram は単語の文脈を予測するためのモデルであり、まずコーパスから単語間の関係を学習し、次にその関係を使用して特定の単語の文脈、つまり単語のベクトル表現を表現します。つまり、同じシーケンス内で 2 つの単語が同時に出現する頻度が高くなるほど、2 つの単語のベクトル表現はより類似します。この考え方をグラフに適用し、式に示すように最適化目的関数を定義します。
これら 2 つの重み行列はそれぞれ、単語が異なる役割を果たすときに単語に関連付けられた単語ベクトルを表します。 。 Skip-gram は単語の文脈を予測するためのモデルであり、まずコーパスから単語間の関係を学習し、次にその関係を使用して特定の単語の文脈、つまり単語のベクトル表現を表現します。つまり、同じシーケンス内で 2 つの単語が同時に出現する頻度が高くなるほど、2 つの単語のベクトル表現はより類似します。この考え方をグラフに適用し、式に示すように最適化目的関数を定義します。 
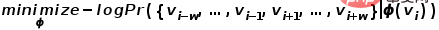
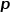 とパラメーター
とパラメーター 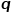 # を定義します。 ##各ランダム ウォークが幅優先サンプリングか深さ優先サンプリングのどちらの傾向にあるかをガイドし、適応性が高くなります。現在ノード
# を定義します。 ##各ランダム ウォークが幅優先サンプリングか深さ優先サンプリングのどちらの傾向にあるかをガイドし、適応性が高くなります。現在ノード 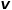 # を訪問していると仮定すると、次にノード
# を訪問していると仮定すると、次にノード 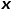 # を訪問する確率は次の式のようになります。 。
# を訪問する確率は次の式のようになります。 。 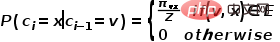
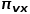
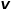 への遷移確率。
への遷移確率。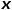 は正規化定数を表します。
は正規化定数を表します。 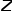
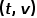 を介してノード v に到達し、次のステップでノード x にアクセスすると仮定します。
を介してノード v に到達し、次のステップでノード x にアクセスすると仮定します。 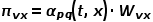 はノード
はノード 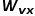 と
と 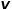 の間のエッジの重みです。 。つまり、グラフが重み付けされていないグラフの場合、
の間のエッジの重みです。 。つまり、グラフが重み付けされていないグラフの場合、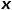 はノードの遷移確率を直接決定します。グラフが重み付きグラフの場合、
はノードの遷移確率を直接決定します。グラフが重み付きグラフの場合、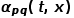 とエッジの重み
とエッジの重み 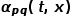 の積により、最終的な遷移確率が決まります。ノードの 。
の積により、最終的な遷移確率が決まります。ノードの 。 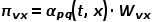 は次の式に従って計算できます。
は次の式に従って計算できます。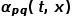 はノード # です。
はノード # です。 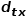 ## とノード
## とノード 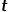 の間の最短パス距離。
の間の最短パス距離。 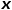 #歩行サンプルがノード
#歩行サンプルがノード 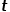
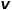 (1)
(1) 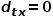
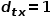 の場合、ノード
の場合、ノード 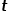 とノード # Common を選択します
とノード # Common を選択します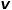 ## の隣接ノード (ノード
## の隣接ノード (ノード 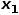 など)。
など)。 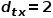 の場合、ノード を選択します
の場合、ノード を選択します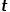 無関係なノード
無関係なノード 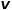 に隣接するノード (ノード
に隣接するノード (ノード 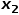 や # など)
や # など) 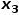 。
。 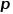 は、前のホップ ノードに戻る確率を制御します。パラメーター
は、前のホップ ノードに戻る確率を制御します。パラメーター 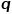 は、ネットワークのローカル構造情報を調査するか、グローバル構造情報を調査するかを詳細に制御します。DeepWalk モデルは、実際には ## です。 # および
は、ネットワークのローカル構造情報を調査するか、グローバル構造情報を調査するかを詳細に制御します。DeepWalk モデルは、実際には ## です。 # および 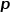 の値が 1 に設定されている場合の Node2Vec モデル。
の値が 1 に設定されている場合の Node2Vec モデル。 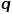
以上がグラフ埋め込みアルゴリズムに関する簡単な説明の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

