ホームページ >バックエンド開発 >Python チュートリアル >時系列特徴抽出のための Python と Pandas のコード例
時系列特徴抽出のための Python と Pandas のコード例
- 王林転載
- 2023-04-12 17:43:081790ブラウズ
Pandas と Python を使用して、時系列データから移動平均、自己相関、フーリエ変換などの意味のある特徴を抽出します。
まえがき
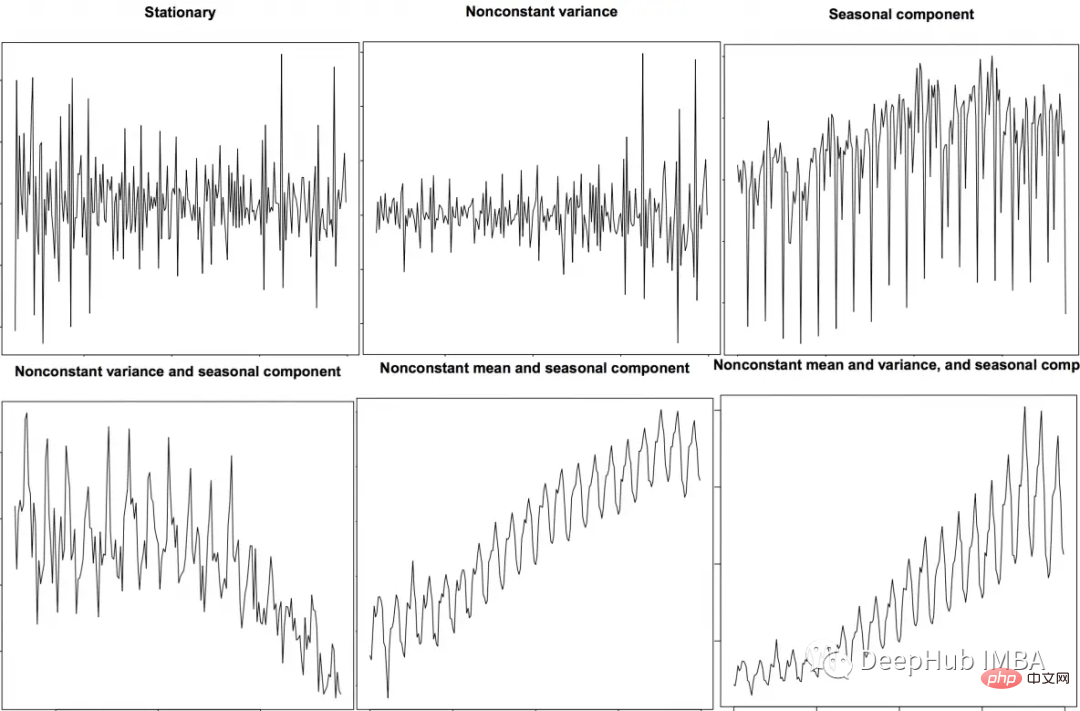
時系列分析は、さまざまな業界 (金融、経済、ヘルスケアなど) の傾向を理解して予測するための強力なツールです。特徴抽出はこのプロセスの重要なステップであり、生データを、予測と分析用のモデルのトレーニングに使用できる意味のある特徴に変換することが含まれます。この記事では、Python と Pandas を使用した時系列特徴抽出手法について説明します。
特徴抽出について詳しく説明する前に、時系列データを簡単に確認してみましょう。時系列データは、時間順にインデックス付けされた一連のデータ ポイントです。時系列データの例には、株価、気温測定値、交通データなどがあります。時系列データは単変量または多変量の場合があります。単変量時系列データには変数が 1 つだけありますが、多変量時系列データには複数の変数があります。
- リサンプリング
- 移動平均
- 指数平滑法
- 自己相関
- フーリエ変換
import pandas as pd
# create a time series with minute frequency
ts = pd.Series([1, 2, 3, 4, 5], index=pd.date_range('2022-01-01', periods=5, freq='T'))
# downsample to daily frequency
daily_ts = ts.resample('D').sum()
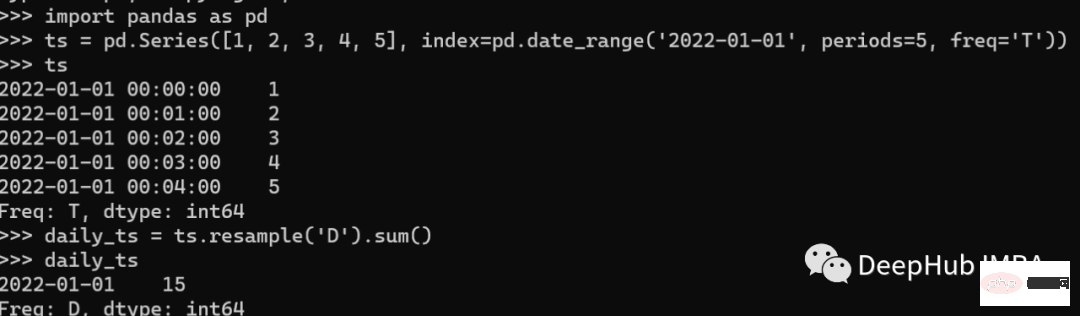
print(daily_ts) 上の例では、分の頻度で時系列を作成し、 resample() メソッドを使用してそれを毎日の頻度にサンプリングします。
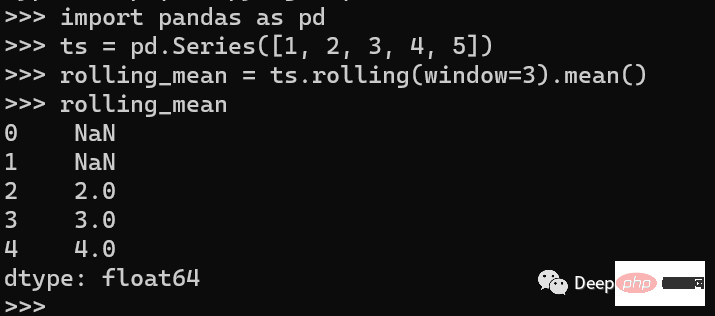
import pandas as pd # create a time series ts = pd.Series([1, 2, 3, 4, 5]) # calculate the rolling mean with a window size of 3 rolling_mean = ts.rolling(window=3).mean() print(rolling_mean)時系列を作成し、rolling() メソッドを使用して、ウィンドウ サイズ 3 の移動平均を計算します。
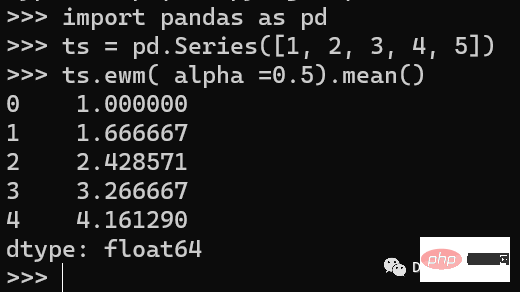
import pandas as pd ts = pd.Series([1, 2, 3, 4, 5]) ts.ewm( alpha =0.5).mean()
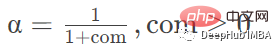
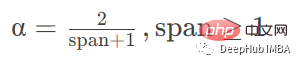 #halflife は半減期に基づく減衰を指定します
#halflife は半減期に基づく減衰を指定します
##alpha は平滑化係数 α# を指定します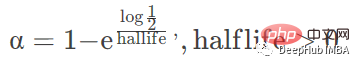
##上記 4 つのパラメータはすべて平滑化係数 α を指定しますが、最初の 3 つは条件に基づいて計算され、最後の 1 つは手動で指定されるため、たとえば、上の例では、0.5
 min_periods ウィンドウの値を使用して観測の最小数を手動で設定しています (デフォルトは 0)。
min_periods ウィンドウの値を使用して観測の最小数を手動で設定しています (デフォルトは 0)。
adjust =Ture时公式如下:
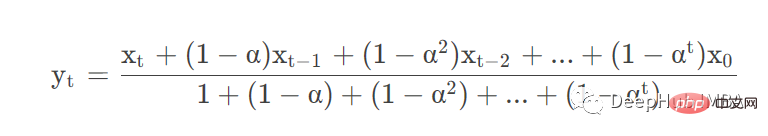
adjust =False
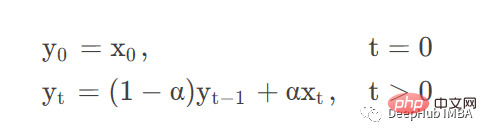
4、Autocorrelation
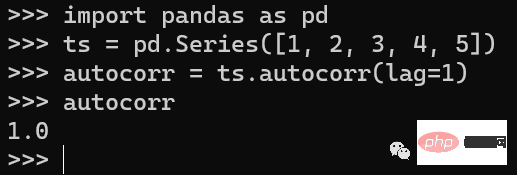
Autocorrelation 自相关是一种用于测量时间序列与其滞后版本之间相关性的技术。可以识别数据中重复的模式。Pandas提供了autocorr()方法来计算自相关性。
import pandas as pd # create a time series ts = pd.Series([1, 2, 3, 4, 5]) # calculate the autocorrelation with a lag of 1 autocorr = ts.autocorr(lag=1) print(autocorr)
5、Fourier Transform
Fourier Transform 傅里叶变换是一种将时间序列数据从时域变换到频域的技术。可以识别数据中的周期性模式。我们可以使用numpy的fft()方法来计算时间序列的快速傅里叶变换。
import pandas as pd import numpy as np # create a time series ts = pd.Series([1, 2, 3, 4, 5]) # calculate the Fourier transform fft = pd.Series(np.fft.fft(ts).real) print(fft)
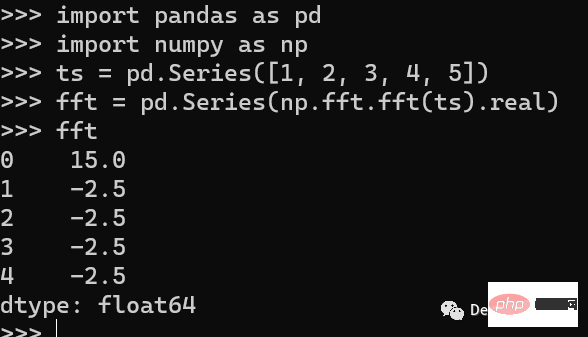
这里我们只显示了实数的部分。
总结
在本文中,我们介绍了几种使用Python和Pandas的时间序列特征提取技术。这些技术可以帮助将原始时间序列数据转换为可用于分析和预测的有意义的特征,在训练机器学习模型时,这些特征都可以当作额外的数据输入到模型中,可以增加模型的预测能力。
以上が時系列特徴抽出のための Python と Pandas のコード例の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

