ホームページ >テクノロジー周辺機器 >AI >理論コンピュータ科学者ボアズ・バラク氏:ディープラーニングは「単純な統計」ではなく、両者の距離はますます遠ざかっている
理論コンピュータ科学者ボアズ・バラク氏:ディープラーニングは「単純な統計」ではなく、両者の距離はますます遠ざかっている
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB転載
- 2023-04-12 17:34:161418ブラウズ
1990 年代、スタンフォード大学の生物情報学の著名な教授であるロブ ティブシラニは、機械学習と統計のさまざまな概念を単純かつ大まかに対応付けるための語彙を作成しました。

#この表は、機械学習の基本的な理解を提供する一方で、深層学習または機械学習の概念を単に要約したものです。統計におけるこの言葉の意味は、ディープラーニングの性質に対するほとんどの人々の認知バイアスの原因にもなります。つまり、ディープラーニングは「単純な統計」です。
しかし、深く議論すると、この種の認識は、研究者が深層学習の成功の本質的な理由を理解することをある程度妨げてきました。今年6月の記事「ディープラーニングと(古典)統計の間の不安な関係」の中で、著名なハーバード大学教授で理論コンピュータ科学者であるボアズ・バラク氏は、ディープラーニングと統計を比較・区別し、ディープラーニングの基本を指摘した。 . 構成要素は統計とは大きく異なります。
Boaz Barak 氏は重要な見解を述べました。モデルの目的の観点から、予測と観察に重点を置くのであれば、ブラック ボックス特性を備えた深層学習モデルが最適である可能性があります。ただし、物事の因果関係を理解し、解釈可能性を向上させたい場合は、「単純な」モデルの方がパフォーマンスが向上する可能性があります。これは、馬毅氏、曹英氏、沈祥陽氏の3人の科学者が先月提案した、知能の2原則のうちの1つを構成する「単純さ」という見解と一致する。
同時に、ボアズ・バラク氏は、統計モデルのフィッティングと数学の学習という 2 つの異なるシナリオのケースを示して、深層学習との互換性について議論しました。深層学習の場合、統計モデルのフィッティングとほぼ同じであり、より深いレベルでは、深層学習の大部分は「生徒にスキルを教える」シナリオで捉えることができます。
統計学習が深層学習において重要な役割を果たしているのは疑いの余地がありません。しかし確かなことは、統計的な観点だけではディープ ラーニングを理解するための全体像を提供できないということです。ディープ ラーニングのさまざまな側面を理解するには、依然としてさまざまな観点からアプローチする必要があります。
#以下はボアズ・バラクの議論です:1
モデルフィッティングにおける予測と説明何千年もの間、科学者は観察にモデルを当てはめてきました。たとえば、『科学の哲学』の本の表紙で言及されているように、エジプトの天文学者プトレマイオスは惑星運動の独創的なモデルを提案しました。プトレマイオスのモデルは地心的 (つまり、惑星が地球の周りを公転する) でしたが、優れた予測精度をもたらす一連の「ノブ」 (具体的には周転円) を持っていました。対照的に、コペルニクスの元の地動説モデルは、太陽の周りの惑星の円軌道を想定していました。これはプトレマイオスのモデルよりも単純で (「調整可能なノブ」が少なく)、全体的に正確ですが、観測値の予測の精度は低くなります。
(コペルニクスは後に独自の周転円を追加し、プトレマイオスの性能に匹敵しました。)プトレマイオスとコペルニクスのモデルは比類のないものです。予測を行うために「ブラック ボックス」が必要な場合は、プトレマイオスの地心モデルが優れています。そして、「内部を覗く」ことができ、星の運動を説明するための理論的な出発点として機能する単純なモデルが必要な場合は、コペルニクスのモデルの方が優れています。
実際、ケプラーは最終的にコペルニクスのモデルを楕円軌道に改良し、惑星運動の 3 つの法則を提案しました。これにより、ニュートンは地球に適用されるものと同じものを使用できるようになりました。重力の法則はそれらを説明します。 。この目的を達成するには、地動説モデルが予測を提供する単なる「ブラック ボックス」ではなく、「変動部分」がほとんどない単純な数式によって与えられることが重要です。天文学は長年にわたり、統計手法を開発するためのインスピレーションの源でした。ガウスとルジャンドルは 1800 年頃に小惑星やその他の天体の軌道を予測するために最小二乗回帰を (独立して) 発明しました; 1847 年のコーシーの勾配降下法の発明も天文予測が動機でした。
物理学では、(少なくとも場合によっては)「すべてを手に入れる」ことができます。つまり、最高の予測精度とデータの最良の説明につながる「正しい」理論を見つけることができます。これは、次のような原理によって説明されます。オッカムの剃刀 このような見解は、単純さ、予測力、説明的洞察力がすべて相互に一貫しているという前提を捉えています。しかし、他の多くの分野では、説明 (より一般的には洞察) と予測という 2 つの目標の間に緊張関係があります。 観測結果を予測したいだけの場合は、「ブラック ボックス」が最適な選択かもしれません。ただし、因果関係モデル、一般原則、または重要な特徴を抽出する場合は、理解しやすく説明しやすい単純なモデルの方が適している可能性があります。
モデルの正しい選択は、その目的によって異なります。たとえば、多くの個人の遺伝子発現と表現型 (たとえば、特定の病気) を含むデータセットを考えてみます。個人が病気になる可能性を予測することが目標の場合、多くの場合、そのタスクに最適なモデルを使用したいと思うでしょう。どんなに複雑であっても、あるいはどれほど多くの遺伝子に依存していても。対照的に、ウェットラボでさらに研究するためにいくつかの遺伝子を同定することが目的の場合、たとえ非常に正確であっても、洗練されたブラックボックスの用途は限られます。
2001 年、レオ ブライマンは統計モデリングに関する有名な記事「統計モデリング: 2 つの文化」の中でこの点を効果的に説明しました。 「データ モデリング文化」はデータを説明する単純な生成モデルに焦点を当てますが、「アルゴリズム モデリング文化」はデータがどのように生成されるかを理解せず、データを予測できるモデルを見つけることに焦点を当てます。 ブライマン氏は、統計は第一の文化に支配されすぎており、その集中が「無関係な理論や疑わしい科学的結論につながり」、「統計学者が刺激的な新しい疑問を研究するのを妨げている」と考えています。
## #しかし、ブライマンの論文は物議を醸しました。ブラッド・エフロンも意見の一部には同意しますが、「最初に見たとき、レオ・ブライマンの刺激的な論文は、操作するノブがたくさんあるブラックボックスを支持して、単純さと科学的洞察を拒否しているように見えます。二度目に見ると、それはまだ同じです。」 」しかし、最近の記事 (「予測、推定、帰属」) でエフロンは、「ブライマンの方が私よりも先見の明があったことが判明しました。 純粋な予測アルゴリズムが 21 世紀の統計の脚光を占めており、その開発の方向性は、Leo が以前に述べたこととほぼ同じです。機械学習が「深い」かどうかにかかわらず、それはすべて、ブライマンが第 2 文化と呼ぶもの、つまり、長い間流通してきた 予測に焦点を当てる に属します。たとえば、Duda と Hart の 1973 年の教科書「Deconstructing Distributions: A Pointwise Framework of Learning」と Highleyman の 1962 年の論文「The Design and Analysis of Pattern Recognition Experiments」は、今日の深層学習の実践者にとって非常によく知られています。
同様に、Highleyman の手書き文字データセットと、Chow がデータセットに適合させるために使用したアーキテクチャ (精度は約 58%) も、現代の読者の共感を呼びます。
3
ディープラーニングはなぜ違うのですか? 
1992 年に、Stuart Geman、Elie Bienenstock、Rene Doursat は、「ニューラル ネットワークとバイアス/バリアン ジレンマ」というタイトルの論文を共同執筆しました。この論文では、たとえば、「現在のフィードフォワード ニューラル ネットワークは、機械認識と機械学習における困難な問題を解決するには、それらはほとんど不十分です。」特に、汎用ニューラル ネットワークでは困難なタスクをうまく解決することができず、ニューラル ネットワークが成功する唯一の方法は手作業で設計された機能を使用することであると信じています。彼らの言葉を借りれば、「重要な機能は、統計的手法を通じて学習するのではなく、組み込みまたは「組み込まれている」必要があります。
」今になって考えると、彼らは完全に間違っていました。さらに、Transformer などの最新のニューラル ネットワーク アーキテクチャは、当時の畳み込みネットワークよりもさらに多用途です。しかし、彼らの間違いの背後にある理由を理解するのは興味深いことです。 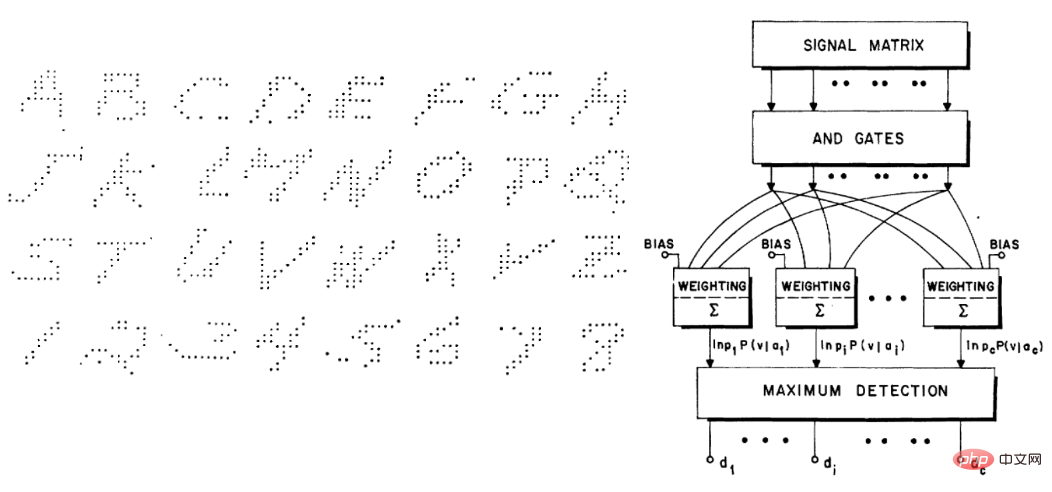
彼らが間違いを犯した理由は、ディープラーニングが他の学習方法とは確かに異なるからだと思います。 アプリオリな現象は次のとおりです。深層学習には、最近傍モデルやランダム フォレストなどの予測モデルが 1 つだけあるようです。より多くの「ノブ」があるかもしれませんが、それは質的な違いではなく量的な違いのようです。 PW アンドレソンの言葉を借りれば、「多ければ多いほど違う」ということです。
物理学では、スケールが数桁変化すると、それを説明するためにまったく異なる理論が必要になることがよくあります。同様のことがディープラーニングにも当てはまります。実際、 深層学習は、高レベルの観点からは方程式 (および Python コード) が同じに見えても、従来のモデル (パラメトリックまたはノンパラメトリック) とはまったく異なる動作をします。
これを説明するために、2 つのまったく異なる例の学習プロセスを見てみましょう: 統計モデルの適合と、生徒への数学の学習の指導。 #シナリオ A: 統計モデルのフィッティング
一般的に、統計モデルをデータにフィッティングする手順は次のとおりです。1. いくつかのデータ x と y を観察してみましょう。 x は n ## の行列とみなすことができます。ここで、
は対応するノイズであり、簡単にするために加法ノイズが使用され、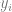 は正しい真のラベルです。 )
は正しい真のラベルです。 )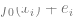
 2. 最適化アルゴリズムを実行することで、モデル
2. 最適化アルゴリズムを実行することで、モデル 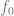 # をデータに適合させることができるため、## エクスペリエンス# のリスクは最小限です。つまり、最適化アルゴリズムを使用して
# をデータに適合させることができるため、## エクスペリエンス# のリスクは最小限です。つまり、最適化アルゴリズムを使用して
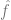 の最小数を見つけます。ここで、
の最小数を見つけます。ここで、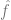 は損失項です (# をキャプチャします)。
は損失項です (# をキャプチャします)。 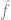 ##y にどれだけ近いか)、
##y にどれだけ近いか)、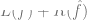 はオプションの正規化項です (
はオプションの正規化項です (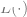 をより単純なモデルに偏らせようとしています)。
をより単純なモデルに偏らせようとしています)。
3. 一般化誤差/損失が小さいため、モデルの全体的な損失が良好であることを願っています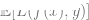 (この予測は、実験データが含まれる全体的なデータに基づいています)得る)。
(この予測は、実験データが含まれる全体的なデータに基づいています)得る)。
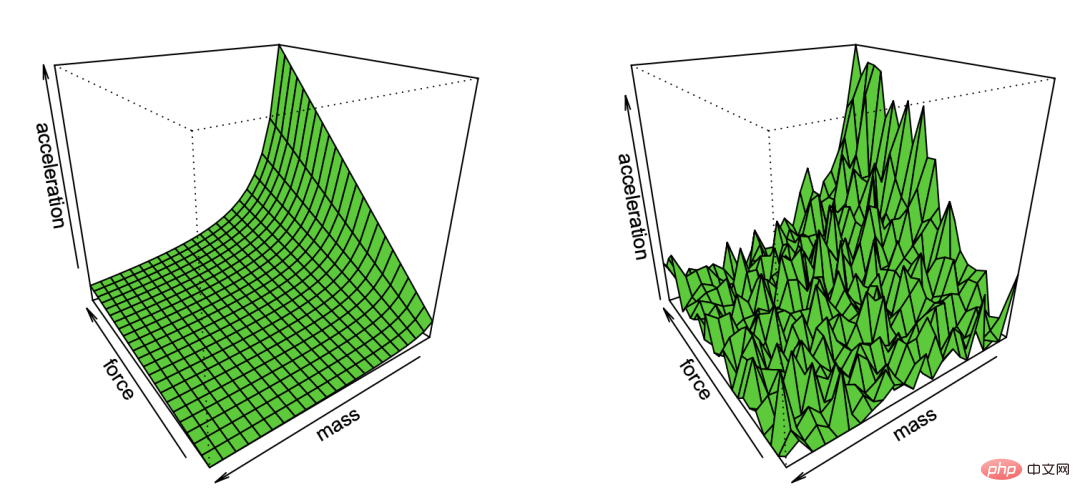
# キャプション: ブラッドリー エフロンがノイズの観察を通じて再現したニュートンの第一法則漫画
この非常に一般的なパラダイムには、最小二乗線形回帰、最近傍法、ニューラル ネットワーク トレーニングなどを含む多くの設定が含まれます。古典的な統計設定では、次のことが観察されると予想されます:
バイアス/分散のトレードオフ: F を最適化されたモデルのセットとして考えます。 (非凸設定にある場合、および/または正則化項がある場合、アルゴリズムの選択と正則化の影響を考慮して、アルゴリズムによって無視できない確率で実装できるモデルのセットを F とすることができます。 )
F の偏差は正しいラベルへの最良の近似値であり、要素 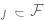 によって達成できます。 F のクラスが大きいほど偏差は小さくなり、
によって達成できます。 F のクラスが大きいほど偏差は小さくなり、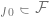 の場合は偏差がゼロになることもあります。ただし、F クラスが大きくなると、そのメンバーシップ範囲を狭めるためにより多くのサンプルが必要になるため、アルゴリズム出力モデルの分散が大きくなります。全体的な汎化誤差は、バイアス項と分散寄与の合計です。
の場合は偏差がゼロになることもあります。ただし、F クラスが大きくなると、そのメンバーシップ範囲を狭めるためにより多くのサンプルが必要になるため、アルゴリズム出力モデルの分散が大きくなります。全体的な汎化誤差は、バイアス項と分散寄与の合計です。
したがって、統計学習ではバイアスと分散のトレードオフが見られることが多く、正しいモデルの複雑さの「ゴルディロックス選択」を通じて全体の誤差を最小限に抑えます。実際、Geman らはまさにそのとおりで、「バイアスと分散のジレンマから生じる基本的な制限は、ニューラル ネットワークを含むすべてのノンパラメトリック推論モデルに適用される」と言って、ニューラル ネットワークに対する悲観的な見方を正当化しています。
より多くのことが常に最善であるとは限りません。 統計学習では、より多くの特徴やデータを取得しても、必ずしもパフォーマンスが向上するとは限りません。 たとえば、無関係な特徴を多く含むデータから学習することはより困難です。同様に、データが 2 つの分布 (例:  と
と  ) のいずれかに由来する混合モデルから学習することは、個々の分布を個別に学習するよりも困難です。
) のいずれかに由来する混合モデルから学習することは、個々の分布を個別に学習するよりも困難です。
#収益の減少。 多くの場合、予測ノイズを何らかのパラメータ まで減らすために必要なデータ ポイントの数は、いくつかのパラメータ k Form 展開の下で  のオーダーになります。この場合、「離陸」するには約 k 個のサンプルが必要で、これを実行すると、収穫逓減システムに直面することになります。つまり、(たとえば) 90% の精度を達成するのに n ポイントかかると仮定すると、次のようになります。精度を 95% に高めるには、さらに約 3n ポイントが必要です。一般に、リソースが増加するにつれて (データ、モデルの複雑さ、計算のいずれであっても)、新しい定性的な機能を解放するのではなく、よりきめ細かい区別を把握したいと考えます。
のオーダーになります。この場合、「離陸」するには約 k 個のサンプルが必要で、これを実行すると、収穫逓減システムに直面することになります。つまり、(たとえば) 90% の精度を達成するのに n ポイントかかると仮定すると、次のようになります。精度を 95% に高めるには、さらに約 3n ポイントが必要です。一般に、リソースが増加するにつれて (データ、モデルの複雑さ、計算のいずれであっても)、新しい定性的な機能を解放するのではなく、よりきめ細かい区別を把握したいと考えます。 
損失とデータへの強い依存。 モデルを高次元データに適合させる場合、小さな詳細が結果に大きな違いを引き起こす可能性があります。統計学者は、完全に異なるデータセットを使用すると、高次元オプティマイザーの数が大きく異なることは言うまでもなく、L1 または L2 正則化機能のような選択が重要であることを知っています。 データ ポイントには、(少なくとも場合によっては) 自然な「困難」はありません。 伝統的に、データ ポイントは分布とは独立してサンプリングされます。決定境界に近い点は分類がより困難になる可能性がありますが、測定値が高次元に集中していることを考えると、ほとんどの点は同様の距離を持つことが予想されます。したがって、少なくとも古典的なデータ分布では、ポイントの難易度が大きく異なることは予想されません。ただし、混合モデルではこの違いの難易度が異なる可能性があるため、上記の他の問題とは異なり、この違いは統計的な設定ではそれほど驚くべきことではありません。 上記とは対照的に、学生にいくつかの特定の数学トピック (導関数の計算など) を教え、一般的なガイダンスを与えることについて話しましょう。必要条件を満たした上で演習を行ってください。これは正式に定義された設定ではありませんが、その定性的特性のいくつかが考慮されます: ## キャプション: IXL Web サイトから具体的な数学を学習してください。スキルの実践 #おおよその配分ではなく、スキルを学びましょう。 この場合、 人の生徒は、一定量の推定量/予測量ではなく、スキルを学習しています。 「スキル」を定義するのは簡単な作業ではありませんが、質的に異なる目標です。特に、関数マッピングの演習が、一部の関連タスク X を解決するための「ブラック ボックス」として使用できない場合でも、これらの問題を解決するときに学生が形成する内部表現は X にとって依然として有用であると考えられます。 多ければ多いほど良いです。 一般的に、学生はより多くの問題やさまざまな種類の質問を練習すると、より良い結果が得られます。しかし実際には、微積分の問題と代数の問題をいくつか行う「ハイブリッド モデル」は、生徒の微積分の成績に影響を与えず、実際に生徒の学習に役立ちます。 「探索」または機能のロックを解除し、自動表示に切り替えます。 ある時点で問題解決の利益は減少しますが、学生は、問題を解決することでコンセプトが「クリック」され、新しい機能が解放される段階を通過しているようです。さらに、生徒が特定の種類の問題を繰り返すと、それらの問題の能力と表現力がより低いレベルに移行し、以前にはなかった問題に対するある程度の自動性を身につけることができるようです。 #パフォーマンス部分は損失やデータとは無関係です。 数学の概念を教える方法は複数あり、たとえ異なる書籍、教育方法、または成績評価システムを使用したとしても、生徒は結局同じ教材と同様の内部表現を学習することになる可能性があります。 数学の演習では、同じ問題を解くためにさまざまな生徒が使用した方法に強い相関関係があることがよく見られます。問題の難易度は固定されているようで、パズルを解く順番も固定されているため、学習プロセスが最適化されます。これは実際に IXL などのプラットフォームが行っていることです。 4
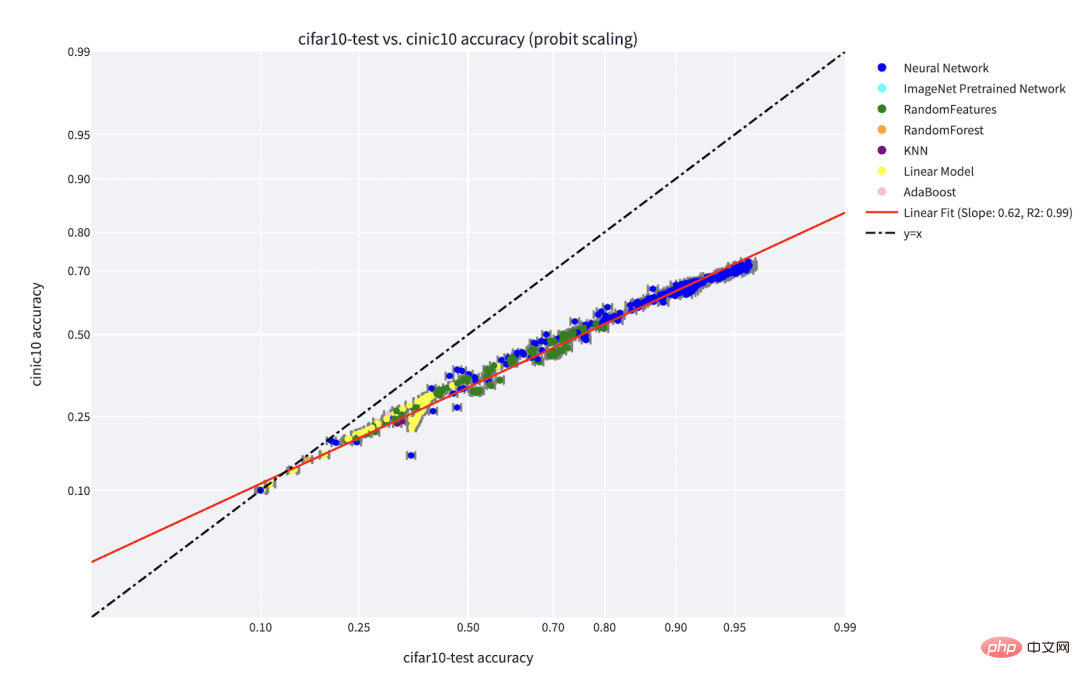
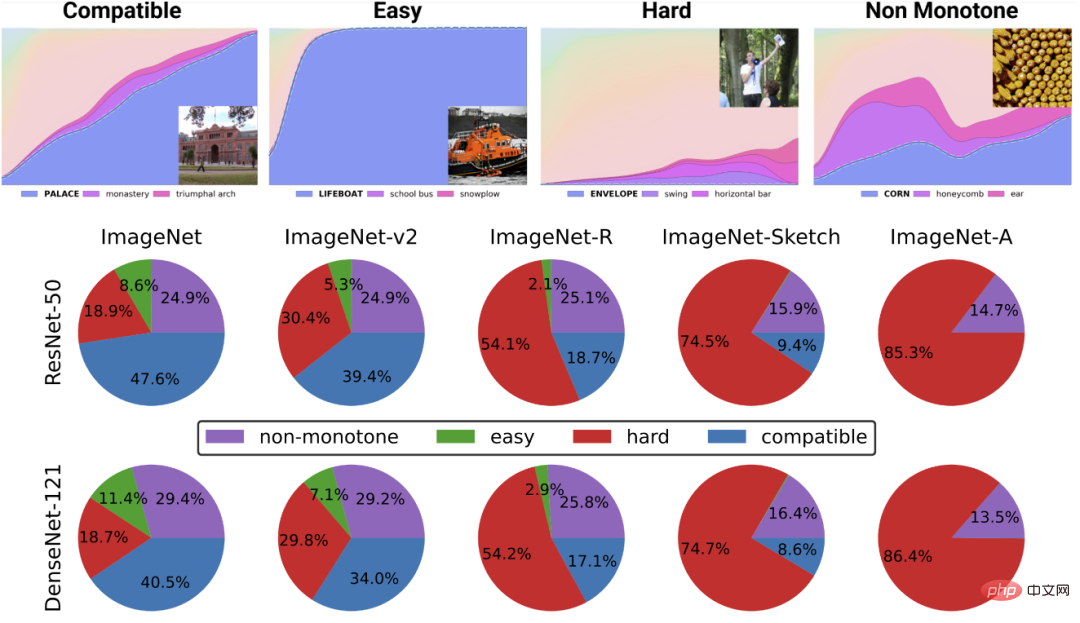
1. データがシーケンス 2. まず関数 3. 次に、完全なラベル付きデータ 関数を近似するのではなく、スキルを学習します。 自己教師あり学習は、関数を近似することではなく、さまざまな下流タスクに使用できる表現を学習することです。これが自然言語処理の主流のパラダイムであると仮定すると、下流のタスクが線形プローブ、微調整、プロンプトのいずれによって取得されるかは二の次です。 多ければ多いほど良いです。 自己教師あり学習では、データ量が増加するにつれて表現の品質が向上します。そして、データは多様であればあるほど良いのです。 # 凡例: Google PaLM モデルのデータセット # #能力のロックを解除します。 リソース (データ、計算、モデル サイズ) が拡大するにつれて、深層学習モデルの不連続な改善が何度も見られ、これは一部の合成環境でも実証されています。 注: モデル サイズが増加するにつれて、PaLM モデルは一部のベンチマークでいくつかの個別の改善を示し (上の図にはサイズに関する警告が 3 つだけあります)、いくつかのコマンドのロックが解除されます。ジョークを説明するように。 #パフォーマンスは、損失やデータとはほとんど関係ありません。 複数の自己教師損失、複数のコントラスト損失と再構成損失が画像に使用されます。言語モデルは、片側再構築 (次のトークンの予測) を使用する場合もあれば、左右のトークンからマスクされた入力を予測することを目的としたマスキング モデルを使用する場合もあります。 わずかに異なるデータセットを使用することも可能ですが、これは効率に影響する可能性があります。 ただし、「合理的な」選択が行われている限り、一般に、元のリソースは使用された特定の損失またはデータセットよりも優れたパフォーマンスを予測します。 #一部のインスタンスは他のインスタンスよりも困難です。 これは自己教師あり学習に限定されません。データ ポイントには固有の「難易度」が存在する場合があります。 実際には、異なる学習アルゴリズムには異なる「スキル レベル」があり、異なるポイントには異なる「難易度」があることを示す実践的な証拠がいくつかあります。 f は x を正しく分類します。f のスキルによって一方的に増加し、x の難易度によって一方的に減少します)。 「スキルと難易度」パラダイムは、Recht と Miller らが発見した「オンライン精度」現象を最も明確に説明するもので、私が Kaplun、Ghosh、Garg、Nakkiran と共著した論文でもそのことを示しています。データセット 異なる入力が、従来、異なるモデルに対して堅牢であると思われる固有の「難易度の特徴」をどのように持つか。 チャート: Miller et al. のグラフは、CIFAR-10 でトレーニングされ、CINIC-10 でテストされた分類器を示しています。ライン現象の精度
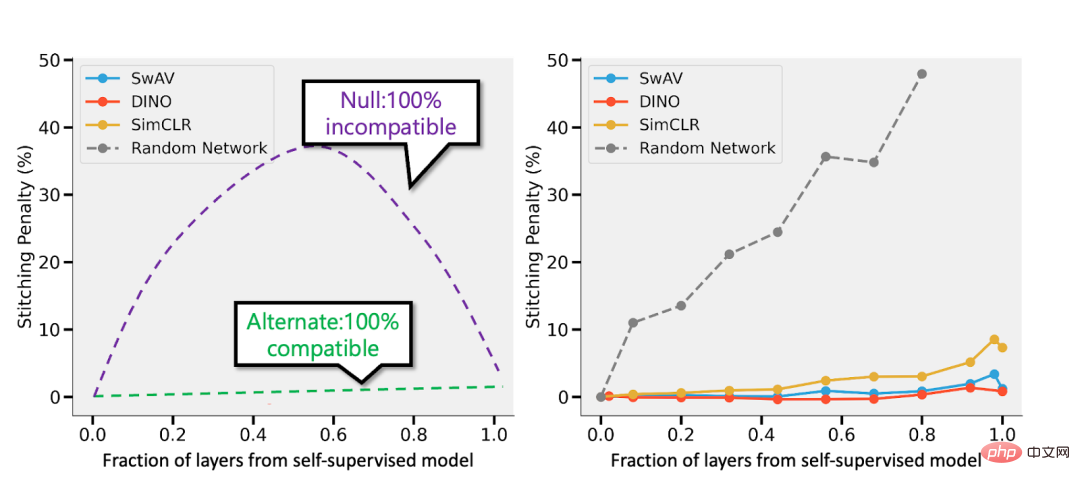
# 分布: 点ごと学習のフレームワーク」を使用して、ますます多くのリソース分類子を取得します。上のグラフは、トレーニング時間によってインデックス付けされた分類器のグローバル精度の関数として、最も可能性の高いクラスのさまざまなソフトマックス確率を示しています。下の円グラフは、さまざまなデータセットをさまざまなタイプのポイントに分類したものを示しています。注目すべきことに、この分解は異なるニューラル アーキテクチャでも同様です。 #トレーニングは教えることです。 大規模モデルの最新のトレーニングは、モデルをデータに適応させるというよりは、学生に教えることに近いようです。 #図: Meta のトレーニング ログからの抜粋 ##シナリオ 1: 教師あり学習 まず第一に、教師あり大規模深層学習の出現は、大規模で高品質のラベル付きデータセット (つまり ImageNet) が利用できるようになったおかげで、ある意味歴史的な偶然です。 別の歴史を想像することも可能です。深層学習は、まず教師なし学習を通じて自然言語処理にブレークスルーをもたらし、その後、ビジョン学習と教師あり学習に移行しました。 第二に、 教師あり学習と自己教師あり学習はまったく異なる損失関数を使用しているにもかかわらず、「舞台裏」では同様に動作するという証拠がいくつかあります。通常、どちらも同じパフォーマンスを達成します。 論文「Revisiting Model Stitching to Compare Neural Representations」でも、同様の内部表現を学習したことが判明しました。具体的には、各 キャプション: ヒントンのチームの論文「大きな自己教師ありモデルは強力な半教師あり学習者である」の表。教師あり学習、微調整 (100%) 自己教師あり、自己教師あり線形検出のパフォーマンスは一般的に類似していることに注意してください。 注: 論文「神経表現を比較するためのモデルステッチングの再検討」の自己監視および監視モデルからの抜粋。左 - 自己教師ありモデルの精度が教師ありモデルよりも 3% 低い場合、完全に互換性のある表現では p 3% のスプライシング ペナルティが発生します (p 層が自己教師ありモデルからのものである場合)。モデルに完全な互換性がない場合、より多くのモデルをつなぎ合わせると精度が大幅に低下することが予想されます。右 - さまざまな自己教師ありモデルを結合した実際の結果。 自己教師あり単純モデルの利点は、特徴学習または「深層学習の魔法」 (深い表現関数の結果) と統計を組み合わせられることです。モデル フィッティング (この表現の上で分離された、線形またはその他の「単純な」分類器によって実行されます) 。 最後に、推測的ではありますが、「メタ学習」は、表現を学習するという事実と同一視されることが多いようです (論文「急速な学習か機能の再利用か? 理解に向けて」を参照) 「有効性」(MAML の詳細については「MAML の詳細」を参照))は、モデルが表面上何に最適化されているかに関係なく、この記事の要点を裏付けるもう 1 つの証拠と見なすことができます。 読者の皆さんは、実際のアプリケーションにおける統計学習モデルと深層学習モデルの違いの典型的な例を省略していることに気づいたかもしれません。 、「バイアスと分散のトレードオフ」の欠如、および過剰パラメータ化されたモデルの優れた一般化能力。 これらの例について詳しく説明しないのには 2 つの理由があります: まず、教師あり学習が実際に自己学習と同等であるかどうかです。 -教師ありの単純な「最下層」学習、そしてその一般化能力について説明できます (詳細については、論文「自己教師あり学習の場合、合理性は一般化を意味する、証明されている」を参照してください)。 #第二に、私は 過剰なパラメータ化は深層学習の成功の鍵ではないと思います。 教師なし/自己教師あり学習モデルでは通常、過剰なパラメーター化はありません。大規模な言語モデルであっても、より大きなデータ セットを持っているだけですが、だからといってそのパフォーマンスの謎が少なくなるわけではありません。 図: 論文「ディープ ブートストラップ フレームワーク: 優れたオンライン学習者は優れたオフライン ジェネラライザーである」の研究結果では、今日のディープ ラーニング アーキテクチャが「過剰なパラメータ化」に悩まされており、パフォーマンスが低下していることが示されています。 「アンダーサンプリング」状態 (モデルがオーバーフィットするまで、多くの世代にわたって限定されたデータでトレーニングされる場合: 上記の「現実世界」) も同様ですが、「アンダーパラメーター化」および「オンライン」の場合にも同様です (モデルがオーバーフィットするまで)。は 1 世代だけトレーニングされ、各サンプルは 1 回だけ表示されます。つまり、上の図の「理想的な世界」です) ディープラーニングにおいて統計学習が重要な役割を果たしているのは間違いありません。ただし、ディープラーニングを単に古典的なモデルよりも多くのノブに適合するモデルとして考えると、その成功の背後にある多くの要因を見落とすことになります。いわゆる「人間の学生」という比喩はさらに不適切です。 深層学習は、同じルールを何度も繰り返し適用する (つまり、経験損失を伴う勾配降下法など) ものの、非常に複雑な結果を生成するという点で、生物学的進化に似ています。ニューラル ネットワークのさまざまなコンポーネントは、表現学習、予測フィッティング、暗黙的な正則化、純粋なノイズなど、さまざまな時点でさまざまなことを学習しているようです。私たちはディープ ラーニングに関する質問に答えるのはもちろん、質問するための適切なレンズをまだ探しています。 まだまだ道は長いですが、私たちは皆さんを励ますために協力していきます。 シナリオ B: 数学の学習
では、上の 2 つの比喩のうち、現代のディープ ラーニングをより適切に説明しているのはどれでしょうか。具体的には、なぜディープ ラーニングがこれほど成功しているのでしょうか?統計モデルのフィッティングは、数学やコードとより一貫しているように見えます。実際、標準の Pytorch トレーニング ループは、上で説明したように、経験的なリスクの最小化を通じて深いネットワークをトレーニングします。
 ただし、より深いレベルでは、階層的に、 2 つの設定はあまり明確ではありません。具体的には、特定の学習タスクを修復し、「自己教師あり学習線形プローブ(線形プローブ)」手法を使用して分類アルゴリズムをトレーニングすることで実行できます。アルゴリズムのトレーニングは次のとおりです。
ただし、より深いレベルでは、階層的に、 2 つの設定はあまり明確ではありません。具体的には、特定の学習タスクを修復し、「自己教師あり学習線形プローブ(線形プローブ)」手法を使用して分類アルゴリズムをトレーニングすることで実行できます。アルゴリズムのトレーニングは次のとおりです。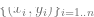 であると仮定します (
であると仮定します (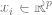 は特定のデータ ポイント (特定の画像など)、
は特定のデータ ポイント (特定の画像など)、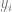 はタグです。
はタグです。 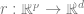 を表すディープ ニューラル ネットワークを見つけます。この関数のトレーニングではデータ ポイント
を表すディープ ニューラル ネットワークを見つけます。この関数のトレーニングではデータ ポイント 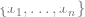 # のみを使用します。 ## ラベルを使用する代わりに、ある種の自己教師あり損失関数を最小限に抑えます。このような損失関数の例としては、再構成やピクチャー・イン・ピクチャー (別の入力 x の一部を復元する)、または対照学習 (
# のみを使用します。 ## ラベルを使用する代わりに、ある種の自己教師あり損失関数を最小限に抑えます。このような損失関数の例としては、再構成やピクチャー・イン・ピクチャー (別の入力 x の一部を復元する)、または対照学習 (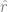 を有意に小さくする
を有意に小さくする 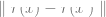 を見つける、
を見つける、 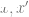 が同じデータ ポイントの増分である場合、並列関係は 2 つのランダムな点間の並列関係よりもはるかに小さくなります)。
が同じデータ ポイントの増分である場合、並列関係は 2 つのランダムな点間の並列関係よりもはるかに小さくなります)。 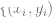 を使用して、線形分類器
を使用して、線形分類器 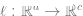 (C はクラス) を当てはめます。数値)を使用して、クロスエントロピー損失を最小限に抑えます。最終的な分類子の結果は、
(C はクラス) を当てはめます。数値)を使用して、クロスエントロピー損失を最小限に抑えます。最終的な分類子の結果は、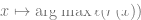 のマッピングになりました。ステップ 3 は線形分類器にのみ適しているため、 ステップ 2 (深層ネットワークの自己教師あり学習) で「魔法」が起こります。 自己教師あり学習では、次のような特性が見られます。
のマッピングになりました。ステップ 3 は線形分類器にのみ適しているため、 ステップ 2 (深層ネットワークの自己教師あり学習) で「魔法」が起こります。 自己教師あり学習では、次のような特性が見られます。 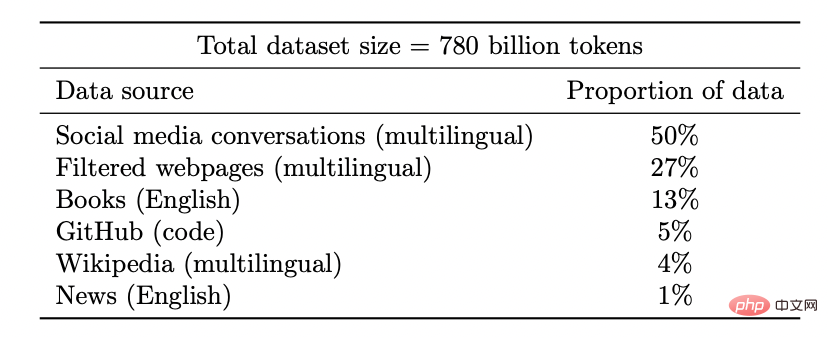
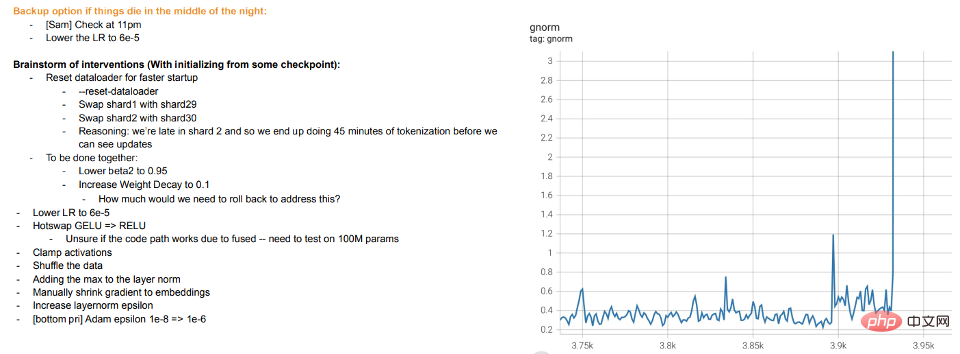 学生が理解できない場合や疲れているように見える場合は、「休憩」を取るか、他のことを試してください (トレーニングの偏差) 。 Meta の大規模モデルのトレーニング ログは有益です。ハードウェアの問題に加えて、トレーニング中のさまざまな最適化アルゴリズムの切り替え、「ホットスワップ」アクティベーション関数 (GELU から RELU) の検討など、いくつかの介入も確認できます。モデルのトレーニングを表現の学習ではなくデータのフィッティングとして考える場合、後者はあまり意味がありません。
学生が理解できない場合や疲れているように見える場合は、「休憩」を取るか、他のことを試してください (トレーニングの偏差) 。 Meta の大規模モデルのトレーニング ログは有益です。ハードウェアの問題に加えて、トレーニング中のさまざまな最適化アルゴリズムの切り替え、「ホットスワップ」アクティベーション関数 (GELU から RELU) の検討など、いくつかの介入も確認できます。モデルのトレーニングを表現の学習ではなくデータのフィッティングとして考える場合、後者はあまり意味がありません。 
以下 2 つの状況について説明します。
 について、自己監視でトレーニングされた深い d モデルの最初の k 層を教師ありモデルの最後の d-k 層で「ステッチ」し、パフォーマンスをほぼ元の状態に維持することができます。レベル。
について、自己監視でトレーニングされた深い d モデルの最初の k 層を教師ありモデルの最後の d-k 層で「ステッチ」し、パフォーマンスをほぼ元の状態に維持することができます。レベル。 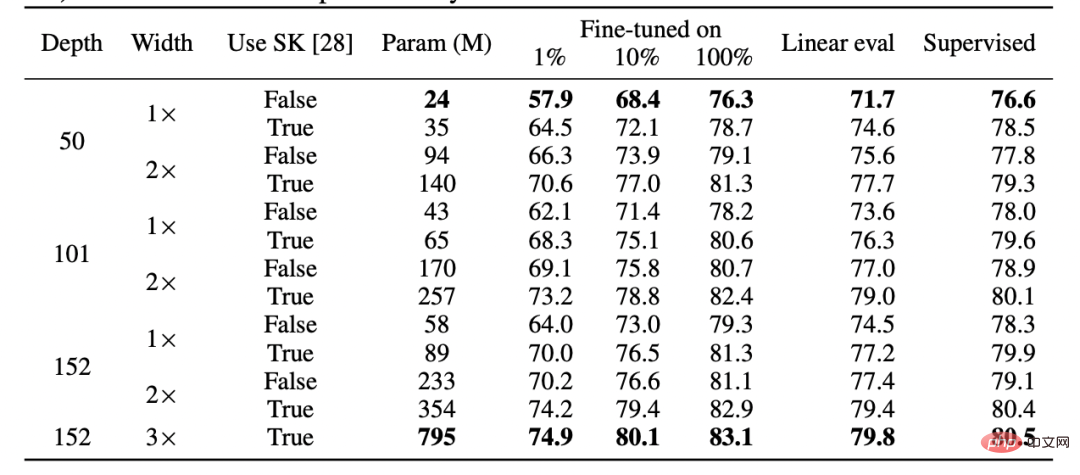
ケース 2: 過剰なパラメータ化
5 まとめ
以上が理論コンピュータ科学者ボアズ・バラク氏:ディープラーニングは「単純な統計」ではなく、両者の距離はますます遠ざかっているの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

