翻訳者 | Zhu Xianzhong
査読者 | Sun Shujuan
従来の球面 CNN は高解像度分類に拡張できない タスク。この論文では、関連情報を保持しながら入力データの次元を削減でき、回転等分散特性も備えた新しいタイプの球面散乱層を紹介します。
散乱ネットワークは、畳み込みフィルターを最初から学習するのではなく、ウェーブレット解析から事前に定義された畳み込みフィルターを使用して機能します。散乱層の重みは学習されるのではなく特別に設計されるため、散乱層を 1 回限りの前処理ステップとして使用することができ、それによって入力データの解像度が低下します。私たちのこれまでの経験では、初期散乱層を備えた球状 CNN は数千万ピクセルの解像度まで拡張できることが示されており、これは従来の球状 CNN 層では以前は達成できなかった偉業です。
従来の球面深層学習手法には計算が必要です
球面 CNN (ドキュメント 1、2、3) は、機械学習におけるさまざまなタイプの問題を解決するのに非常に役立ちます。これらの問題の多くには、平面上で自然に表現できないデータ ソースがあります (これについての入門については、 にある前回の記事を参照してください: https://towardsdatascience.com/geometric- deep-learning-for-spherical-データ-55612742d05f)。
球面 CNN の重要な特徴は、球面データの回転と等変であることです (この記事では、回転等変法に焦点を当てます)。実際には、これは球状 CNN が優れた一般化特性を備えていることを意味し、3D オブジェクトのメッシュを、回転方法 (およびさまざまな回転のトレーニング中にメッシュが表示されるかどうか) に関係なく分類するなどの作業を行うことができます。
最近の 公開記事で 記述しました Kagenovaチーム球面CNNの計算効率を向上させるために開発された一連の開発成果(参考アドレス: https://towardsdatascience .com/efficient-generalized-spherical-cnns-1493426362ca)。私たちが 採用した メソッド - 効率的な一般化球面 CNN - 両方の は 伝統 球面 CNN の等分散特性により、 計算効率も向上します (文献 1)。ただし、このような計算効率の向上にも関わらず、球面 CNN は依然として比較的低解像度のデータに限定されています。 これは、、球状 CNN は現在、通常より高い分解能を必要とする撹拌には適用できないことを意味しますアプリケーション シナリオ におけるデータ # (宇宙論的データ分析や仮想現実の 360 度コンピューター ビジョンなど) ### 田畑######。最近公開された 記事では、効率的な一般球面 CNN ## を柔軟に調整するための球面散乱層ネットワークを紹介しました。 #来解像度を向上させます (ドキュメント 4)。この記事では内容を確認します。 高解像度の入力データをサポートするハイブリッド アプローチ効率的なユニバーサル球面 CNN (参考 1) を開発する際、球 A を構築する非常に効果的な方法を発見しました。 CNN アーキテクチャへのハイブリッド アプローチ。ハイブリッド球面 CNN は、同じネットワーク内でさまざまなスタイルの球面 CNN レイヤーを使用できるため、開発者は処理のさまざまな段階でさまざまなタイプのレイヤーの利点を得ることができます。 上の図は、ハイブリッド球面 CNN アーキテクチャの例を示しています (注意: これらのレイヤーは単一のものではなく、いくつかの異なるスタイルのレイヤーです)球状 CNN 層)。
Scattering Networks on Spheres は、このハイブリッド アプローチを継続し、既存の球状アーキテクチャに接続できる新しい球状 CNN レイヤーを導入します。効率的な一般球面 CNN を高次元に拡張するには、この新しい層には次の特性が必要です。
- 計算サポートによるスケーラビリティ
- 情報を低周波にブレンドして、後続のレイヤーを低解像度で実行できるようにします
- 回転等分散
- 安定性と局所的に不変な表現を提供します(つまり、効率的な表現空間を提供する)
# 散乱ネットワーク層には、上で列挙したこれらの特性をすべて満たす可能性があると判断しました。
球面上の散乱ネットワーク
ユークリッド環境で Mallat によって最初に提案された散乱ネットワーク (参考文献 5) は、固定畳み込みフィルタリングを持つものとみなすことができます。CNN の場合、これらはフィルターはウェーブレット解析から派生します。散乱ネットワークは、特にデータが限られている場合、つまり畳み込みフィルターの学習が難しい場合に、従来の (ユークリッド) コンピューター ビジョンに非常に役立つことが証明されています。次に、散乱ネットワーク層の内部動作、散乱ネットワーク層が前のセクションで定義された要件をどのように満たすか、球面データ解析用に散乱ネットワーク層を開発する方法について簡単に説明します。
散乱層内のデータ処理は、3 つの基本操作によって実行されます。最初の構成要素は固定ウェーブレット畳み込みで、これはユークリッド CNN で使用される通常の学習畳み込みに似ています。ウェーブレット畳み込み後、散乱ネットワークは結果の表現にモジュール式非線形アプローチを適用します。最後に、スキャッタリングは、通常の CNN のプーリング層といくつかの類似点を備えたローカル平均化アルゴリズムを実行するスケーリング関数を利用します。これら 3 つの構成要素を繰り返し適用すると、入力データが計算ツリーに分散され、処理のさまざまな段階で結果の表現 (CNN チャネルと同様) がツリーから抽出されます。これらの操作の簡略図を以下に示します。

#この図は、球状信号 f の球状散乱ネットワークを示しています。信号は、赤いノードで表される絶対値活性化関数と組み合わせられたカスケード球面ウェーブレット変換を介して伝播されます。散乱ネットワークの出力は、これらの信号を球面ウェーブレット スケーリング関数に投影することによって取得され、散乱係数は青色のノードで表されます。
従来のディープラーニングの観点から見ると、分散型ネットワークの運用は少しわかりにくいように思えるかもしれません。ただし、説明されている各計算操作には特定の目的があり、ウェーブレット解析の信頼できる理論的結果を利用することを目的としています。
散乱ネットワークにおけるウェーブレット畳み込みは、入力データから関連情報を抽出するために慎重に導出されます。たとえば、自然画像の場合、ウェーブレットは、高周波数のエッジと低周波数のオブジェクトの一般的な形状に関連する情報を特に抽出するために定義されます。したがって、平面設定では、散乱ネットワーク フィルターは従来の CNN フィルターといくつかの類似点がある可能性があります。同じことが球面設定にも当てはまり、スケール離散ウェーブレットを使用します (詳細については参考文献 4 を参照)。
ウェーブレット フィルターは固定されているため、初期散乱層は 1 回適用するだけでよく、トレーニング プロセス全体を通じて繰り返し適用する必要はありません (従来の CNN の初期層など) )。これにより、散乱ネットワークは計算的にスケーラブルになり、上記の機能 1 の要件を満たします。さらに、散乱層は入力データの次元を削減します。これは、下流の CNN 層をトレーニングするときに、散乱表現をキャッシュするために使用する必要があるストレージ スペースが限られているだけであることを意味します。
ウェーブレット畳み込みの後に、モジュール式非線形手法が続きます。まず、これにより、ニューラル ネットワーク層に非線形特性が注入されます。次に、モジュラス演算により、入力信号の高周波情報が低周波データに混合され、上記の要件 2 が満たされます。以下の図は、モジュラス非線形計算の前後のデータのウェーブレット表現の頻度分布を示しています。

モジュラス計算を適用した後、結果の信号をスケーリング関数に投影します。スケーリング関数は、従来の CNN のプーリング関数の操作と同様に、表現結果から低周波情報を抽出します。
私たちは、球面散乱ネットワークの理論上の等分散特性を経験的にテストしました。テストは、信号を回転して散乱ネットワークに送り、その結果の表現を、散乱ネットワークを通過して回転計算を実行した後の入力データの結果の表現と比較することによって実行されます。以下の表のデータから、特定の深さの等分散誤差が低く、上記の要件 3 を満たしていることがわかります (通常、実際には、1 つのパスの深さが 2 つのパスの深さを超えることはありません。信号エネルギーはすでに捕捉されています)。 深さの異なる球面散乱ネットワークの回転等分散誤差 ついに理論的に証明されましたユークリッド散乱ネットワークは、小さな差分や歪みに対して安定しています。(Documentation5)。 現在、 この結果は、コンパクトなリーマン多様体 (文書 6) 上の散乱ネットワーク、特に球面に拡張されています 環境 (ドキュメント4)。実際には、視差形態に対する安定性は、入力がわずかに変更された場合でも、散乱ネットワークによって計算された表現が大きく変わらないことを意味します (幾何学的な深層学習における安定性の役割の議論については、以前の投稿 を参照してください) , アドレスは https://towardsdatascience.com/a-brief-introduction-to-geometric-deep-learning-dae114923ddb) です。 したがって、散乱ネットワークは、 その後の学習を効率的に実行できる良好なパフォーマンスの表現空間を提供し、上記の要件 4 を満たします。 スケーラブルで回転等変な球面 CNN
散布ネットワークは特定の入力の固定表現を持っているため、散布ネットワーク レイヤーはトレーニングの開始時にデータセット全体に 1 回適用でき、結果の低次元表現は次の場所にキャッシュされます。後続の層をトレーニングします。幸いなことに、散布表現では次元が削減されているため、散布表現を保存するために必要なディスク容量は比較的少なくて済みます。この新しい球面散乱層の存在により、効率的な一般化球面 CNN を高解像度の分類問題の領域に拡張できます。 宇宙マイクロ波背景放射異方性の分類 宇宙学者は、宇宙マイクロ波背景放射を分析する方法に非常に興味を持っています。これらの方法は、宇宙全体の宇宙マイクロ波背景放射の分布における非ガウス特性を検出できるため、理論に重要な意味を持ちます。初期宇宙の、非常に重要な意味を持つ。この分析方法は、天文学的な解像度まで拡張できる必要もあります。 CMB シミュレーションを解像度 L = 1024 でガウスまたは非ガウスとして分類することで、散乱ネットワークがこれらの要件を満たしていることを示します。散乱ネットワークは、これらのシミュレーションを 95.3% の精度で分類することに成功しました。これは、低解像度の従来の球面 CNN によって達成される 53.1% よりもはるかに優れています。
この論文では、下流のタスクのための重要な情報を保持しながら、入力表現の次元を圧縮する球面散乱層の機能を調査しました。これにより、散乱層が高解像度の球体分類タスクに非常に役立つことがわかりました。これにより、宇宙論的データ分析や高解像度 360 画像/ビデオ分類など、これまで困難だった潜在的なアプリケーションへの扉が開かれます。ただし、セグメンテーションや深度推定など、高密度の予測を必要とするコンピューター ビジョンの問題の多くは、高次元の出力と高次元の入力の両方を必要とします。最後に、等分散を維持しながら出力表現の次元を高めることができる、制御可能な球状 CNN 層を開発する方法が、Kagenova 開発者による現在の研究テーマです。これらについては次の記事で説明します。 [1]Cobb、Wallis、Mavor-Parker、Marignier、Price、d'Avezac、McEwen、効率的な一般化球面 CNN、ICLR (2021) 、 arXiv:2010.11661 [2] コーエン、ガイガー、ケーラー、ウェリング、球面 CNN、ICLR (2018)、arXiv:1801.10130 [ 3] Esteves, Allen-Blanchette, Makadia, Daniilidis, Learning SO(3) Equivariant Representations with Spherical CNNs, ECCV (2018), arXiv:1711.06721 [4] McEwen, Jason , Wallis、Christopher、Mavor-Parker、Augustin N.、Scattering Networks on the Sphere for Scalable and Rotationally Equivariant Spherical CNNs、ICLR (2022)、arXiv:2102.02828 [5] Bruna 、 Joan、Stéphane Mallat、Invariant scattering convolution network、IEEE Transaction on Pattern Analysis and Machine Intelligence (2013) [6] Perlmutter、Michael、他、Geometric wavelet scattering network onコンパクト リーマン多様体、数学的および科学的機械学習PMLR (2020)、arXiv:1905.10448 Zhu Xianzhong、51CTO コミュニティ エディター、51CTO エキスパート ブログ、講師、濰坊市の大学のコンピューター教師であり、フリーランスのプログラミング業界のベテランです。 #元のタイトル: 球状深層学習を高解像度の入力データに拡張する 、著者: Jason McEwen、Augustin Mavor-Parker


概要
参考文献
翻訳者紹介
以上が球面ディープラーニングを高解像度の入力データにスケーリングするの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 踊りましょう:私たちの人間のニューラルネットを微調整するための構造化された動きApr 27, 2025 am 11:09 AM
踊りましょう:私たちの人間のニューラルネットを微調整するための構造化された動きApr 27, 2025 am 11:09 AM科学者は、彼らの機能を理解するために、人間とより単純なニューラルネットワーク(C. elegansのものと同様)を広く研究してきました。 ただし、重要な疑問が生じます。新しいAIと一緒に効果的に作業するために独自のニューラルネットワークをどのように適応させるのか
 新しいGoogleリークは、Gemini AIのサブスクリプションの変更を明らかにしますApr 27, 2025 am 11:08 AM
新しいGoogleリークは、Gemini AIのサブスクリプションの変更を明らかにしますApr 27, 2025 am 11:08 AMGoogleのGemini Advanced:Horizonの新しいサブスクリプションティア 現在、Gemini Advancedにアクセスするには、1か月あたり19.99ドルのGoogle One AIプレミアムプランが必要です。 ただし、Android Authorityのレポートは、今後の変更を示唆しています。 最新のGoogle p
 データ分析の加速がAIの隠されたボトルネックをどのように解決しているかApr 27, 2025 am 11:07 AM
データ分析の加速がAIの隠されたボトルネックをどのように解決しているかApr 27, 2025 am 11:07 AM高度なAI機能を取り巻く誇大宣伝にもかかわらず、エンタープライズAIの展開内に大きな課題が潜んでいます:データ処理ボトルネック。 CEOがAIの進歩を祝う間、エンジニアはクエリの遅い時間、過負荷のパイプライン、
 MarkitDown MCPは、任意のドキュメントをマークダウンに変換できます!Apr 27, 2025 am 09:47 AM
MarkitDown MCPは、任意のドキュメントをマークダウンに変換できます!Apr 27, 2025 am 09:47 AMドキュメントの取り扱いは、AIプロジェクトでファイルを開くだけでなく、カオスを明確に変えることです。 PDF、PowerPoint、Wordなどのドキュメントは、あらゆる形状とサイズでワークフローをフラッシュします。構造化された取得
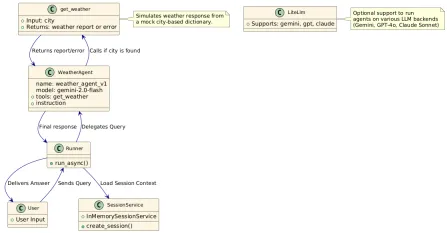 建物のエージェントにGoogle ADKを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:42 AM
建物のエージェントにGoogle ADKを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:42 AMGoogleのエージェント開発キット(ADK)のパワーを活用して、実際の機能を備えたインテリジェントエージェントを作成します。このチュートリアルは、ADKを使用して会話エージェントを構築し、GeminiやGPTなどのさまざまな言語モデルをサポートすることをガイドします。 w
 効果的な問題解決のためにLLMを介したSLMの使用 - 分析VidhyaApr 27, 2025 am 09:27 AM
効果的な問題解決のためにLLMを介したSLMの使用 - 分析VidhyaApr 27, 2025 am 09:27 AMまとめ: Small Language Model(SLM)は、効率のために設計されています。それらは、リソース不足、リアルタイム、プライバシーに敏感な環境の大手言語モデル(LLM)よりも優れています。 特にドメインの特異性、制御可能性、解釈可能性が一般的な知識や創造性よりも重要である場合、フォーカスベースのタスクに最適です。 SLMはLLMSの代替品ではありませんが、精度、速度、費用対効果が重要な場合に理想的です。 テクノロジーは、より少ないリソースでより多くを達成するのに役立ちます。それは常にドライバーではなく、プロモーターでした。蒸気エンジンの時代からインターネットバブル時代まで、テクノロジーの力は、問題の解決に役立つ範囲にあります。人工知能(AI)および最近では生成AIも例外ではありません
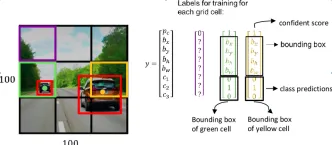 コンピュータービジョンタスクにGoogle Geminiモデルを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:26 AM
コンピュータービジョンタスクにGoogle Geminiモデルを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:26 AMコンピュータービジョンのためのGoogleGeminiの力を活用:包括的なガイド 大手AIチャットボットであるGoogle Geminiは、その機能を会話を超えて拡張して、強力なコンピュータービジョン機能を網羅しています。 このガイドの利用方法については、
 Gemini 2.0 Flash vs O4-Mini:GoogleはOpenaiよりもうまくやることができますか?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs O4-Mini:GoogleはOpenaiよりもうまくやることができますか?Apr 27, 2025 am 09:20 AM2025年のAIランドスケープは、GoogleのGemini 2.0 FlashとOpenaiのO4-Miniの到着とともに感動的です。 数週間離れたこれらの最先端のモデルは、同等の高度な機能と印象的なベンチマークスコアを誇っています。この詳細な比較


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

AtomエディタMac版ダウンロード
最も人気のあるオープンソースエディター

ドリームウィーバー CS6
ビジュアル Web 開発ツール

WebStorm Mac版
便利なJavaScript開発ツール

DVWA
Damn Vulnerable Web App (DVWA) は、非常に脆弱な PHP/MySQL Web アプリケーションです。その主な目的は、セキュリティ専門家が法的環境でスキルとツールをテストするのに役立ち、Web 開発者が Web アプリケーションを保護するプロセスをより深く理解できるようにし、教師/生徒が教室環境で Web アプリケーションを教え/学習できるようにすることです。安全。 DVWA の目標は、シンプルでわかりやすいインターフェイスを通じて、さまざまな難易度で最も一般的な Web 脆弱性のいくつかを実践することです。このソフトウェアは、

ホットトピック
 7760
7760 15
15 1644
1644 14
14 1399
1399 52
52 1293
1293 25
25 1234
1234 29
29



