最も一般的に使用されている機械学習アルゴリズムのトップ 10 の図解!

機械学習の分野では、「世界にフリーランチは存在しない」という格言があります。つまり、あらゆる問題に対して最良の効果をもたらすアルゴリズムは存在しないということです。この理論は特に教師あり学習です。重要。

たとえば、ニューラル ネットワークが常にデシジョン ツリーよりも優れているとは言えず、またその逆も同様です。モデルの実行は、データ セットのサイズや構造など、多くの要因の影響を受けます。

したがって、データのテスト セットを使用してパフォーマンスを評価し、最適なものを選択しながら、問題に基づいてさまざまなアルゴリズムを試す必要があります。

もちろん、試行するアルゴリズムは問題に関連している必要があり、鍵となるのは機械学習の主なタスクです。たとえば、家を掃除したい場合、掃除機、ほうき、またはモップを使用することはできますが、シャベルをつかんで穴を掘り始めることはありません。

機械学習の基礎を理解したいと考えている機械学習の初心者向けに、データ サイエンティストが使用する機械学習アルゴリズムのトップ 10 をここに示します。これにより、誰もがより優れた学習を行えるように、これらのトップ 10 のアルゴリズムの特徴を紹介します。ご理解の上、お申し込みの上、見に来てください。

01 線形回帰

線形回帰は、おそらく統計と機械学習において最もよく知られており、最も理解しやすいアルゴリズムの 1 つです。

予測モデリングは主に、モデルの誤差を最小限に抑えること、または解釈可能性を犠牲にして最も正確な予測を行うことに関係しているためです。私たちはさまざまな分野からアルゴリズムを借用、再利用、盗用しており、ある程度の統計知識が関係しています。

線形回帰は、入力変数の特定の重み (B) を求めることによって、入力変数 (x) と出力変数 (y) の間の線形関係を記述する方程式によって表されます。

#線形回帰

例: y = B0 B1 * x

入力 x が与えられた場合、y を予測します。線形回帰学習アルゴリズム目標は、係数 B0 と B1 の値を見つけることです。

線形回帰モデルは、通常の最小二乗法や勾配降下最適化の線形代数ソリューションなど、さまざまな手法を使用してデータから学習できます。

線形回帰は 200 年以上前から存在しており、広範囲に研究されてきました。この手法を使用する場合の経験則としては、非常に類似した (相関のある) 変数を削除し、可能であればデータからノイズを除去することです。これは素早く簡単なテクニックであり、最初のアルゴリズムとしては適しています。

02 ロジスティック回帰

ロジスティック回帰は、機械学習が統計分野から借用するもう 1 つの手法です。これは、二項分類問題 (2 つのクラス値を持つ問題) のための特別な方法です。

ロジスティック回帰は、両方の目的が各入力変数の重み値を見つけることであるという点で線形回帰に似ています。線形回帰とは異なり、出力の予測値は、ロジスティック関数と呼ばれる非線形関数を使用して変換されます。

論理関数は大きな S のように見え、任意の値を 0 から 1 の範囲に変換できます。これは、ロジスティック関数の出力に対応するルールを適用し、値を 0 と 1 に分類し (たとえば、IF が 0.5 未満の場合は 1 を出力)、クラス値を予測できるため便利です。

ロジスティック回帰

モデルの独自の学習方法により、ロジスティック回帰を通じて行われた予測をクラスに属する確率の計算にも使用できます。 0 またはクラス 1 。これは、多くの理論的根拠を必要とする問題に役立ちます。

線形回帰と同様、ロジスティック回帰は、出力変数に関連していない属性や、互いによく似ている (相関している) 属性を削除すると、より効果的に機能します。これは、バイナリ分類問題を迅速に学習して効果的に処理するモデルです。

03 線形判別分析

従来のロジスティック回帰は、二項分類問題に限定されています。 3 つ以上のクラスがある場合は、線形判別分析 (LDA) が推奨される線形分類手法です。

LDA の表現は非常に単純です。これは、各カテゴリに基づいて計算されたデータの統計的プロパティで構成されます。単一の入力変数の場合、これには次のものが含まれます。

各カテゴリの平均値。

すべてのカテゴリにわたって計算された分散。

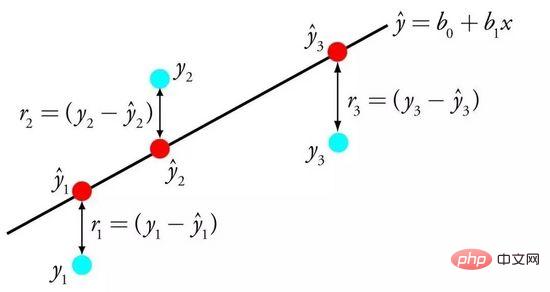
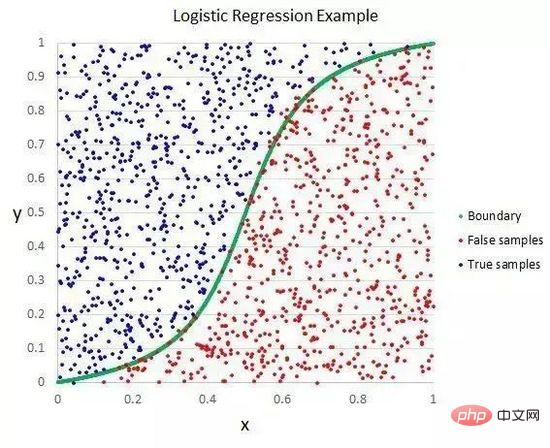
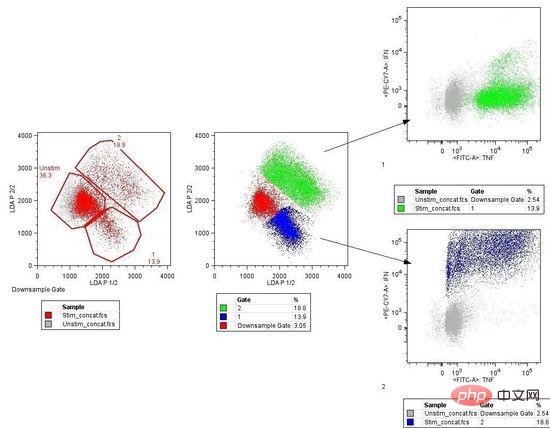
#線形判別分析

LDA は、各クラスの判別値を計算し、最大値を持つクラスの予測を行うことによって実行されます。この手法では、データがガウス分布 (釣鐘曲線) であることを前提としているため、最初にデータから外れ値を手動で削除することが最善です。これは、分類予測モデリング問題におけるシンプルかつ強力なアプローチです。

04 分類と回帰ツリー

デシジョン ツリーは機械学習にとって重要なアルゴリズムです。

デシジョン ツリー モデルはバイナリ ツリーで表すことができます。はい、これはアルゴリズムとデータ構造からなるバイナリ ツリーであり、特別なことは何もありません。各ノードは、単一の入力変数 (x) とその変数の左右の子を表します (変数が数値であると仮定します)。

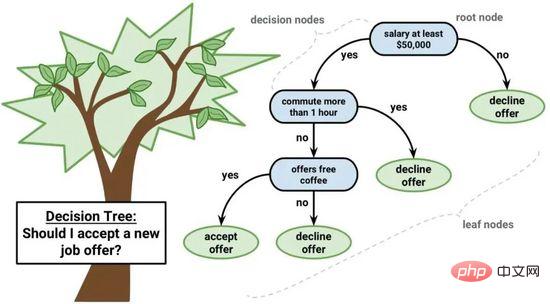
デシジョン ツリー

ツリーのリーフ ノードには、予測を行うために使用される出力変数 (y) が含まれています。予測は、ツリーをトラバースし、特定のリーフ ノードに到達したときに停止し、リーフ ノードのクラス値を出力することによって実行されます。

デシジョン ツリーは学習速度と予測速度が速いです。予測は多くの問題に対して正確であることが多く、データに対して特別な準備を行う必要はありません。

05 Naive Bayes

Naive Bayes は、シンプルですが非常に強力な予測モデリング アルゴリズムです。

モデルは、トレーニング データから直接計算できる 2 種類の確率で構成されます: 1) 各クラスの確率、2) 各 x 値が与えられたクラスの条件付き確率。確率モデルを計算したら、ベイズの定理を使用して新しいデータを予測するために使用できます。データが数値の場合、これらの確率を簡単に推定できるように、ガウス分布 (釣鐘曲線) を仮定するのが一般的です。

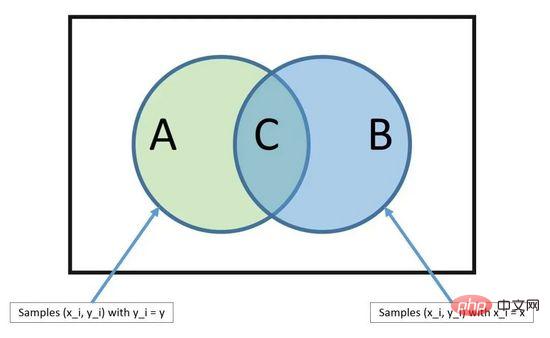
ベイズの定理

単純ベイズが素朴と呼ばれる理由は、各入力変数が独立していると仮定しているためです。これは実際のデータでは非現実的な強力な仮定ですが、この手法は大規模な複雑な問題に対して依然として非常に効果的です。

06 K 最近傍

KNN アルゴリズムは非常にシンプルで、非常に効果的です。 KNN のモデルは、トレーニング データ セット全体によって表されます。とても簡単なことではありませんか？

トレーニング セット全体で最も類似した K 個のインスタンス (近傍) を検索し、これらの K 個のインスタンスの出力変数を要約することで、新しいデータ ポイントを予測します。回帰問題の場合、新しい点は平均出力変数である可能性があり、分類問題の場合、新しい点は最頻値カテゴリ値である場合があります。

成功の秘訣は、データ インスタンス間の類似性を判断する方法にあります。属性がすべて同じスケールにある場合、最も簡単な方法は、各入力変数間の差から直接計算できるユークリッド距離を使用することです。

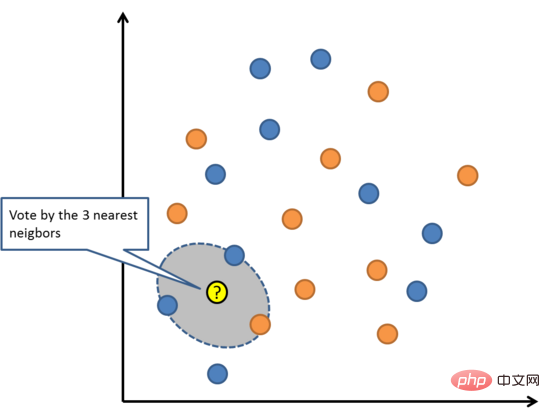
K 最近傍法

KNN は、すべてのデータを保存するために大量のメモリまたはスペースを必要とする可能性がありますが、計算は予測が必要な場合にのみ実行されます (または勉強します）。予測の精度を維持するために、いつでもトレーニング セットを更新および管理することもできます。

高次元環境 (多数の入力変数) では、距離または近さの概念が崩れる可能性があり、アルゴリズムに悪影響を与える可能性があります。このような出来事は次元の呪いとして知られています。また、出力変数の予測に最も関連する入力変数のみを使用する必要があることも意味します。

07 学習ベクトル量子化

K 最近傍法の欠点は、トレーニング データ セット全体を維持する必要があることです。学習ベクトル量子化 (略して LVQ) は、任意の数のトレーニング インスタンスを一時停止して正確に学習できる人工ニューラル ネットワーク アルゴリズムです。

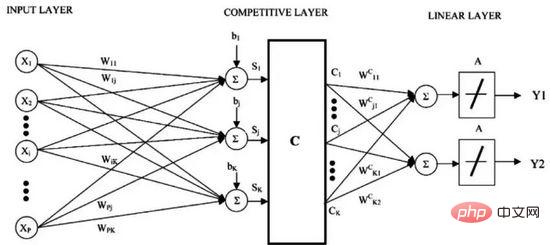
学習ベクトル量子化

LVQ は、コードブック ベクトルのコレクションによって表されます。まずベクトルをランダムに選択し、トレーニング データ セットに適応するために複数回繰り返します。学習後、コードブック ベクトルは K 最近傍法と同様に予測に使用できます。各コードブック ベクトルと新しいデータ インスタンス間の距離を計算して、最も類似した近傍 (最良一致) を見つけ、最も一致するユニットのクラス値、または回帰の場合は実際の値を予測として返します。データを同じ範囲 (0 と 1 の間など) に制限すると、最良の結果が得られます。

KNN がデータセットで良好な結果をもたらすことがわかった場合は、LVQ を使用して、トレーニング データセット全体を保存するためのメモリ要件を削減してみてください。

08 サポート ベクター マシン

サポート ベクター マシンは、おそらく最も人気があり、議論されている機械学習アルゴリズムの 1 つです。

超平面は、入力変数空間を分割する線です。 SVM では、カテゴリ (カテゴリ 0 またはカテゴリ 1) に従って入力変数空間内の点を分離するために超平面が選択されます。これは 2 次元空間内の線とみなすことができ、すべての入力点はこの線によって完全に分離できます。 SVM 学習アルゴリズムは、超平面がカテゴリを最適に分離できるようにする係数を見つけることです。

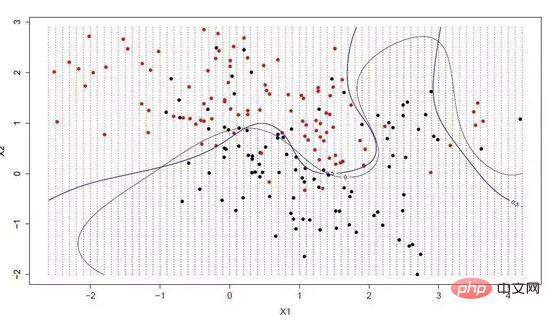
サポート ベクター マシン

超平面と最も近いデータ ポイントの間の距離は境界と呼ばれ、境界が最も大きい超平面が最良の選択です。同時に、これらの近いデータ ポイントのみが超平面の定義と分類器の構築に関連しており、これらの点はサポート ベクトルと呼ばれ、超平面をサポートまたは定義します。具体的な実践では、最適化アルゴリズムを使用して、境界を最大化する係数値を見つけます。

SVM は、おそらく最も強力なすぐに使用できる分類器の 1 つであり、データセットで試してみる価値があります。

09 バギングとランダム フォレスト

ランダム フォレストは、最も人気があり強力な機械学習アルゴリズムの 1 つです。これは、ブートストラップ集約またはバギングと呼ばれる統合機械学習アルゴリズムです。

ブートストラップは、データのサンプルから平均などの量を推定するための強力な統計手法です。多数のサンプル データを取得して平均を計算し、すべての平均を平均して真の平均のより正確な推定値を取得します。

同じ方法がバギングでも使用されますが、統計モデル全体を推定する代わりにデシジョン ツリーが最も一般的に使用されます。トレーニング データをマルチサンプリングし、各データ サンプルのモデルを構築します。新しいデータに対して予測を行う必要がある場合、各モデルは予測を行い、その予測を平均して、真の出力値をより適切に推定します。

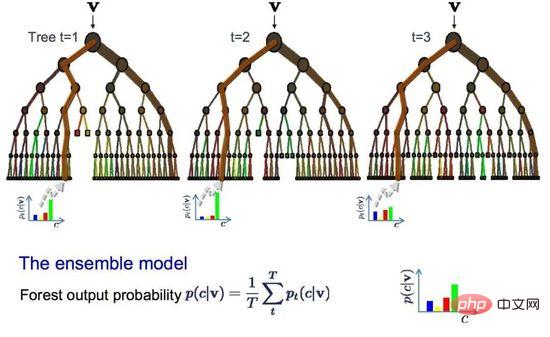
ランダム フォレスト

ランダム フォレストは決定木を調整したものです。最適な分割点を選択するのと比較して、ランダム フォレストはランダム性を導入することによって実現されます。 。

結果として、各データ サンプルに対して作成されたモデルは互いにより異なりますが、それでも独自の意味では正確です。予測結果を組み合わせることで、潜在的な正確な出力値をより適切に推定できます。

高分散アルゴリズム (デシジョン ツリーなど) を使用して良好な結果が得られた場合、このアルゴリズムを追加するとさらに良好な結果が得られます。

10 ブースティングと AdaBoost

ブースティングは、いくつかの弱分類器から強い分類器を作成するアンサンブル手法です。まずトレーニング データからモデルを構築し、次に 2 番目のモデルを作成して、最初のモデルのエラーを修正しようとします。トレーニング セットが完全に予測するか、上限に達するまでモデルを継続的に追加します。

AdaBoost は、バイナリ分類用に開発された初めて真に成功したブースティング アルゴリズムであり、ブースティングを理解するための最良の出発点でもあります。現在、AdaBoost に基づいて構築されている最も有名なアルゴリズムは、確率的勾配ブースティングです。

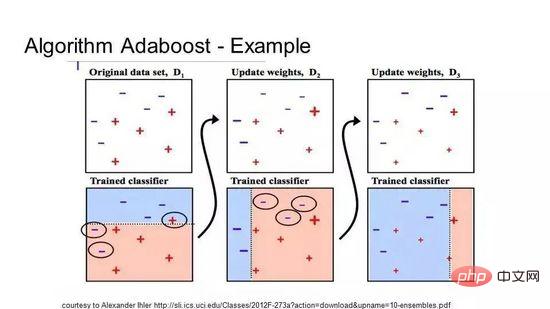
AdaBoost

AdaBoost は、短いデシジョン ツリーでよく使用されます。最初のツリーが作成された後、ツリー上の各トレーニング インスタンスのパフォーマンスによって、次のツリーがそのトレーニング インスタンスにどれだけの注意を払う必要があるかが決まります。予測が難しいトレーニング データにはより大きな重みが与えられ、予測が容易なインスタンスにはより小さな重みが与えられます。モデルは順番に作成され、各モデルの更新はシーケンス内の次のツリーの学習効果に影響を与えます。すべてのツリーが構築された後、アルゴリズムは新しいデータに対して予測を行い、トレーニング データの正確さによって各ツリーのパフォーマンスに重み付けを行います。

アルゴリズムはエラー修正を非常に重視するため、外れ値のないクリーンなデータが非常に重要です。

さまざまな機械学習アルゴリズムに直面したときに初心者が抱く典型的な質問は、「どのアルゴリズムを使用すればよいですか?」です。この質問に対する答えは、次のような多くの要因によって決まります。

• データのサイズ、品質、性質;
• 利用可能なコンピューティング時間;
• タスクの緊急性;
• データを使って何をしたいのか。

経験豊富なデータ サイエンティストでも、さまざまなアルゴリズムを試してみない限り、どのアルゴリズムが最もパフォーマンスが高いかを知る方法はありません。他にも多くの機械学習アルゴリズムがありますが、これらのアルゴリズムが最も人気があります。機械学習を初めて使用する場合は、ここから始めるのが最適です。

以上が最も一般的に使用されている機械学習アルゴリズムのトップ 10 の図解!の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。