Pythonを使って住宅価格予測ガジェットを作ってみよう！

＃＃＃＃＃＃＃＃＃＃＃＃こんにちは、みんな。

これは Kaggle Web サイトからの住宅価格予測のケースで、多くのアルゴリズム初心者にとって最初のコンテストの質問です。

このケースには、EDA、特徴エンジニアリング、モデル トレーニング、モデル融合などを含む、機械学習の問題を解決するための完全なプロセスが含まれています。

住宅価格予測プロセス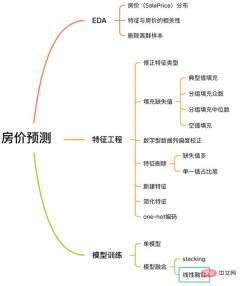

私をフォローして、このケースについて学びましょう。

長い言葉や冗長なコードはなく、単純な説明のみです。

1. EDA

探索的データ分析 (EDA) の目的は、データセットを完全に理解できるようにすることです。このステップで調査するコンテンツは次のとおりです。

##EDA コンテンツ

#1.1 入力データ セット

train = pd.read_csv('./data/train.csv')
test = pd.read_csv('./data/test.csv')

トレーニング サンプル

train と test はそれぞれトレーニング セットとテスト セットで、それぞれ 1460 個のサンプルと 80 個の特徴があります。

SalePrice 列は、予測したい住宅価格を表します。

1.2 住宅価格の分布

私たちのタスクは住宅価格を予測することであるため、データセットで注目すべき中心となるのは住宅価格 (SalePrice) 列の値の分布です。

sns.distplot(train['SalePrice']);

住宅価格の値の分布

図からわかるように、SalePrice 列のピーク値は比較的急峻で、ピーク値は左に傾いています。

また、skew() 関数と kurt() 関数を直接呼び出して、SalePrice の特定の歪度と尖度の値を計算することもできます。

歪度と尖度が比較的大きい状況では、log() を使用して SalePrice 列を平滑化することをお勧めします。

1.3 住宅価格に関連する特徴

SalePrice の分布を理解した後、80 の特徴と SalePrice の間の相関関係を計算できます。

SalePrice に最も関連する 10 個の機能に焦点を当てます。

# 计算列之间相关性
corrmat = train.corr()
# 取 top10
k = 10
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
# 绘图
cm = np.corrcoef(train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()

SalePrice に関連性の高い機能

OverallQual (住宅の材料と仕上げ)、GrLivArea (地上の居住エリア)、GarageCars (ガレージの収容能力)、 TotalBsmtSF (地下エリア) は、SalePrice と強い相関があります。

これらの機能は、後で特徴エンジニアリングを行うときにも焦点を当てます。

1.4 外れ値サンプルの除去

データセットのサンプルサイズは非常に小さいため、外れ値はその後のモデルのトレーニングに役立ちません。

したがって、各数値特性の外れ値を計算し、最も外れ値が多いサンプルを除去する必要があります。

# 获取数值型特征
numeric_features = train.dtypes[train.dtypes != 'object'].index
# 计算每个特征的离群样本
for feature in numeric_features:
outs = detect_outliers(train[feature], train['SalePrice'],top=5, plot=False)
all_outliers.extend(outs)
# 输出离群次数最多的样本
print(Counter(all_outliers).most_common())
# 剔除离群样本
train = train.drop(train.index[outliers])

detect_outliers() は、sklearn ライブラリの LocalOutlierFactor アルゴリズムを使用して外れ値を計算するカスタム関数です。

この時点で、EDA は完了します。最後に、トレーニング セットとテスト セットをマージして、次の特徴エンジニアリングを実行します。

y = train.SalePrice.reset_index(drop=True)
train_features = train.drop(['SalePrice'], axis=1)
test_features = test
features = pd.concat([train_features, test_features]).reset_index(drop=True)

features は、トレーニング セットとテスト セットの機能を組み合わせたもので、以下で処理するデータです。

2. 特徴量エンジニアリング

##特徴量エンジニアリング

2.1 補正特徴量タイプ

MSSubClass (ハウス タイプ)、YrSold (売上年）とMoSold（売上月）はカテゴリ特徴量ですが、数値で表されるためテキスト特徴量に変換する必要があります。

features['MSSubClass'] = features['MSSubClass'].apply(str)
features['YrSold'] = features['YrSold'].astype(str)
features['MoSold'] = features['MoSold'].astype(str)

2.2 特徴量の欠損値の埋め方

欠損値の埋め方には統一した基準がなく、特徴量に応じてどのように埋めるかを決める必要があります。

# Functional：文档提供了典型值 Typ
features['Functional'] = features['Functional'].fillna('Typ') #Typ 是典型值
# 分组填充需要按照相似的特征分组，取众数或中位数
# MSZoning（房屋区域）按照 MSSubClass（房屋）类型分组填充众数
features['MSZoning'] = features.groupby('MSSubClass')['MSZoning'].transform(lambda x: x.fillna(x.mode()[0]))
#LotFrontage（到接到举例）按Neighborhood分组填充中位数
features['LotFrontage'] = features.groupby('Neighborhood')['LotFrontage'].transform(lambda x: x.fillna(x.median()))
# 车库相关的数值型特征，空代表无，使用0填充空值。
for col in ('GarageYrBlt', 'GarageArea', 'GarageCars'):
features[col] = features[col].fillna(0)

2.3 歪度の修正

SalePrice 列の調査と同様に、歪度の高い特徴は平滑化されます。

# skew()方法，计算特征的偏度（skewness）。
skew_features = features[numeric_features].apply(lambda x: skew(x)).sort_values(ascending=False)
# 取偏度大于 0.15 的特征
high_skew = skew_features[skew_features > 0.15]
skew_index = high_skew.index
# 处理高偏度特征，将其转化为正态分布，也可以使用简单的log变换
for i in skew_index:
features[i] = boxcox1p(features[i], boxcox_normmax(features[i] + 1))

2.4 特徴量の削除と追加

ほぼすべてが欠損値であるか、単一値の割合が高い (99.94%) 特徴量は、直接削除できます。

features = features.drop(['Utilities', 'Street', 'PoolQC',], axis=1)

同時に、複数の機能を融合して新しい機能を生成することができます。

モデルが特徴間の関係を学習することが難しい場合がありますが、特徴を手動で融合すると、モデルの学習の困難さが軽減され、効果が向上します。

# 将原施工日期和改造日期融合
features['YrBltAndRemod']=features['YearBuilt']+features['YearRemodAdd']
# 将地下室面积、1楼、2楼面积融合
features['TotalSF']=features['TotalBsmtSF'] + features['1stFlrSF'] + features['2ndFlrSF']

融合した機能はすべて、SalePrice に強く関連する機能であることがわかります。

最後に特徴を単純化し、単調分布の特徴に対して 01 処理を実行します (たとえば、100 個のデータのうち 99 個の値が 0.9 で、もう 1 個のデータの値が 0.1 です)。

features['haspool'] = features['PoolArea'].apply(lambda x: 1 if x > 0 else 0)
features['has2ndfloor'] = features['2ndFlrSF'].apply(lambda x: 1 if x > 0 else 0)

2.6 生成最终训练数据

到这里特征工程就做完了， 我们需要从features中将训练集和测试集重新分离出来，构造最终的训练数据。

X = features.iloc[:len(y), :]
X_sub = features.iloc[len(y):, :]
X = np.array(X.copy())
y = np.array(y)
X_sub = np.array(X_sub.copy())

三. 模型训练

因为SalePrice是数值型且是连续的，所以需要训练一个回归模型。

3.1 单一模型

首先以岭回归（Ridge） 为例，构造一个k折交叉验证模型。

from sklearn.linear_model import RidgeCV
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import KFold
kfolds = KFold(n_splits=10, shuffle=True, random_state=42)
alphas_alt = [14.5, 14.6, 14.7, 14.8, 14.9, 15, 15.1, 15.2, 15.3, 15.4, 15.5]
ridge = make_pipeline(RobustScaler(), RidgeCV(alphas=alphas_alt, cv=kfolds))

岭回归模型有一个超参数alpha，而RidgeCV的参数名是alphas，代表输入一个超参数alpha数组。在拟合模型时，会从alpha数组中选择表现较好某个取值。

由于现在只有一个模型，无法确定岭回归是不是最佳模型。所以我们可以找一些出场率高的模型多试试。

# lasso
lasso = make_pipeline(
RobustScaler(),
LassoCV(max_iter=1e7, alphas=alphas2, random_state=42, cv=kfolds))
#elastic net
elasticnet = make_pipeline(
RobustScaler(),
ElasticNetCV(max_iter=1e7, alphas=e_alphas, cv=kfolds, l1_ratio=e_l1ratio))
#svm
svr = make_pipeline(RobustScaler(), SVR(
C=20,
epsilon=0.008,
gamma=0.0003,
))
#GradientBoosting（展开到一阶导数）
gbr = GradientBoostingRegressor(...)
#lightgbm
lightgbm = LGBMRegressor(...)
#xgboost（展开到二阶导数）
xgboost = XGBRegressor(...)

有了多个模型，我们可以再定义一个得分函数，对模型评分。

#模型评分函数
def cv_rmse(model, X=X):
rmse = np.sqrt(-cross_val_score(model, X, y, scoring="neg_mean_squared_error", cv=kfolds))
return (rmse)

以岭回归为例，计算模型得分。

score = cv_rmse(ridge)
print("Ridge score: {:.4f} ({:.4f})n".format(score.mean(), score.std()), datetime.now(), ) #0.1024

运行其他模型发现得分都差不多。

这时候我们可以任选一个模型，拟合，预测，提交训练结果。还是以岭回归为例

# 训练模型
ridge.fit(X, y)
# 模型预测
submission.iloc[:,1] = np.floor(np.expm1(ridge.predict(X_sub)))
# 输出测试结果
submission = pd.read_csv("./data/sample_submission.csv")
submission.to_csv("submission_single.csv", index=False)

submission_single.csv是岭回归预测的房价，我们可以把这个结果上传到 Kaggle 网站查看结果的得分和排名。

3.2 模型融合-stacking

有时候为了发挥多个模型的作用，我们会将多个模型融合，这种方式又被称为集成学习。

stacking 是一种常见的集成学习方法。简单来说，它会定义个元模型，其他模型的输出作为元模型的输入特征，元模型的输出将作为最终的预测结果。

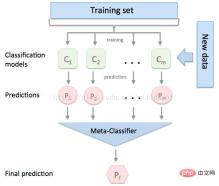
stacking

这里，我们用mlextend库中的StackingCVRegressor模块，对模型做stacking。

stack_gen =
StackingCVRegressor(
regressors=(ridge, lasso, elasticnet, gbr, xgboost, lightgbm),
meta_regressor=xgboost,
use_features_in_secondary=True)

训练、预测的过程与上面一样，这里不再赘述。

3.3 模型融合-线性融合

多模型线性融合的思想很简单，给每个模型分配一个权重（权重加和=1），最终的预测结果取各模型的加权平均值。

# 训练单个模型
ridge_model_full_data = ridge.fit(X, y)
lasso_model_full_data = lasso.fit(X, y)
elastic_model_full_data = elasticnet.fit(X, y)
gbr_model_full_data = gbr.fit(X, y)
xgb_model_full_data = xgboost.fit(X, y)
lgb_model_full_data = lightgbm.fit(X, y)
svr_model_full_data = svr.fit(X, y)
models = [
ridge_model_full_data, lasso_model_full_data, elastic_model_full_data,
gbr_model_full_data, xgb_model_full_data, lgb_model_full_data,
svr_model_full_data, stack_gen_model
]
# 分配模型权重
public_coefs = [0.1, 0.1, 0.1, 0.1, 0.15, 0.1, 0.1, 0.25]
# 线性融合，取加权平均
def linear_blend_models_predict(data_x,models,coefs, bias):
tmp=[model.predict(data_x) for model in models]
tmp = [c*d for c,d in zip(coefs,tmp)]
pres=np.array(tmp).swapaxes(0,1)
pres=np.sum(pres,axis=1)
return pres

到这里，房价预测的案例我们就讲解完了，大家可以自己运行一下，看看不同方式训练出来的模型效果。

回顾整个案例会发现，我们在数据预处理和特征工程上花费了很大心思，虽然机器学习问题模型原理比较难学，但实际过程中往往特征工程花费的心思最多。

以上がPythonを使って住宅価格予測ガジェットを作ってみよう！の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。