グラフ ニューラル ネットワークは Nature サブジャーナルに掲載されましたが、通常のアルゴリズムよりも 104 倍遅いことが明らかになりました。

GNN は近年非常に人気のある分野です。最近、Nature のサブジャーナル論文で GNN を使用して組み合わせ最適化問題を解決する方法が提案され、GNN オプティマイザーのパフォーマンスは既存のソルバーと同等か、それを超えていると主張されました。しかし、この論文にはいくつかの疑問があります。この GNN のパフォーマンスは実際には古典的な貪欲アルゴリズムほど良くなく、速度も貪欲アルゴリズムよりもはるかに遅いと指摘する人もいます (100 万個の変数を伴う問題の場合、貪欲アルゴリズムは、アルゴリズムは GNN よりも 104 倍高速です)。そこで懐疑論者たちは、「この問題を解決するためにこれらの GNN を使用する正当な理由は見当たりません。大ハンマーを使ってナッツを割るようなものです。」彼らは、これらの論文の著者が、最初にこの困難な問題を解決してから、手法の優位性を評価し、ベンチマークを比較します。

近年、ニューラル ネットワークは、離散組み合わせ最適化問題など、応用科学や基礎科学における多くの困難な問題を解決してきました。これは、コンピューティングの限界を理解するための基礎でもあります。

Martin JA Schuetz らの 2022 年の研究「物理学にヒントを得たグラフ ニューラル ネットワークによる組み合わせ最適化」[4] では、物理学にヒントを得た教師なしグラフ ニューラル ネットワーク (GNN) を使用して、このアプローチは、グラフ上の組み合わせ最適化問題を解決するのに有望であると思われ、影響力の高いジャーナル (Nature Machine Intelligence) に掲載されました。この研究では、最大カットと最大独立集合 (MIS) という 2 つの標準的な最適化問題で GNN のパフォーマンスをテストしました。この新しく提案された GNN オプティマイザーには、多くのより大きなインスタンスの問題に拡張できるという、非常に優れた特性があります。

#論文アドレス: https://arxiv.org/pdf/2107.01188.pdf

しかし、最近の新しい論文「大ハンマーでナットを割る: 現代のグラフ ニューラル ネットワークのパフォーマンスが古典的な貪欲アルゴリズムよりも悪いとき」は、Martin JA Schuetz らの研究に疑問を投げかけています。 GNN オプティマイザーは「蚊をすり鉢で叩くのと同じように、大ハンマーでナッツを割っている」ため、リソースが無駄になり、結果も悪くなります。

文書アドレス: https://arxiv.org/abs/2206.13211

MIS 問題は次のように定義されます。n 個のノードと次数が d に固定された無向ランダム正規グラフ (d-RRG) が与えられた場合、独立集合 (IS) は最近傍ペアを含まない頂点のサブセットを指します。 . ; MIS 問題では、最大の IS を見つける必要があり、そのサイズは α と呼ばれます。 MIS は NP 困難問題ですが、多項式時間の最大値にできるだけ近いサイズの IS を見つけるアルゴリズムを見つけたいと考えています。さらに、優れたアルゴリズムは、n の値が大きくなってもパフォーマンスが低下しないようにする必要があります。

Martin JA Schuetz らによって提案された新しい GNN は、非常に大きなグラフ (n≤ 10^6) の IS を見つけることができます: アルゴリズムの実行時間は問題のサイズに比例します: t 〜 n^ 1.7 であり、以下の図 1 に示すように、n が増加してもアルゴリズムのパフォーマンスは安定しています。

ただし、提案された GNN のパフォーマンスを他の利用可能なアルゴリズムと比較する場合、この研究では Boppana とのみ比較します。 Halldorsson (BH) 近似アルゴリズム [8] と比較すると、n≦500 の場合、このアルゴリズムの実行時間は t∼n^2.9 になります。

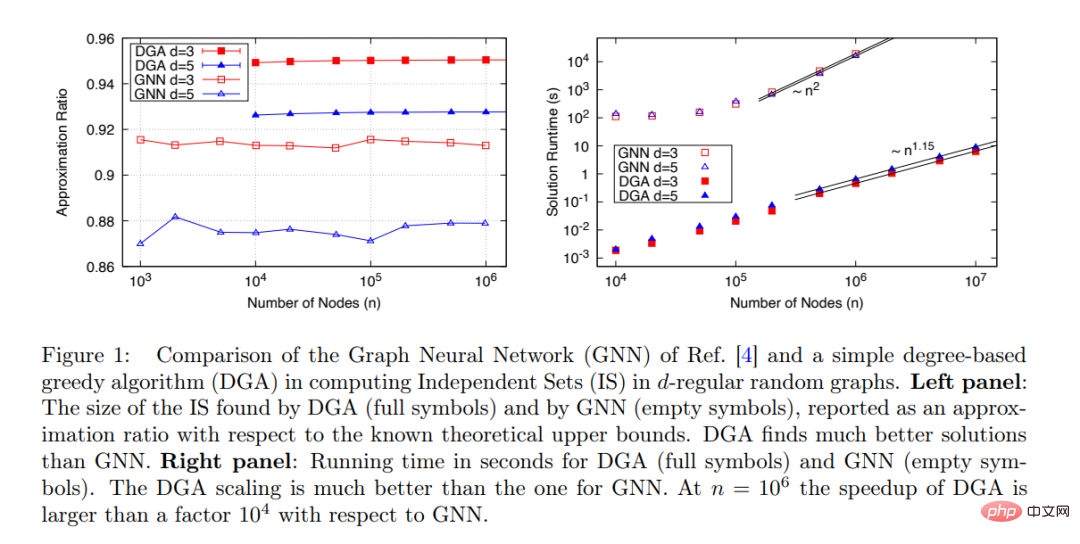
実際には、BH よりもはるかに高速な IS 計算アルゴリズムは他にも多数あり、研究では提案された GNN オプティマイザーとこれらのアルゴリズムを比較する必要があります。その中で最も単純なアルゴリズムは貪欲アルゴリズム (GA) [9] です。次数ベースの貪欲アルゴリズム (DGA) が最適化された後、実行時間はノード数 n にほぼ比例します。

この研究では、Martin JA Schuetz らが提案した GNN オプティマイザー (オープン) と DGA (ソリッド) を比較し、d=3 および d=5 の d-RRG で MIS を見つけます。パフォーマンス。

図 1 (右) に示すように、実行時間と問題サイズ (ノード数) の関係の観点から見ると、DGA は GNN よりもはるかに優れています。 GNN の実行時間はノード数 n とほぼ二次関数の関係があるのに対し、GNN の実行時間は線形の関係があります (指数はおそらく前漸近効果により 1.15 です)。

この研究では、Martin JA Schuetz らの主張「グラフ ニューラル ネットワークに基づくオプティマイザーのパフォーマンスは既存のソルバーと同等かそれ以上であり、現在の SOTA モデルを超える能力がある」と考えています。 「数百万の変数をもつ問題に拡張可能」は精査に耐えられず、実際の実験結果と矛盾しているため、Martin JA Schuetz らは論文を修正する必要がある。

この調査では、DGA のパフォーマンスを詳細に明らかにしており、この単純な貪欲アルゴリズムは最小限のベンチマークとみなされ、新しいアルゴリズムのパフォーマンスは次の水準に達する必要があると考えられています。最低でもDGAよりは優れている 優秀な人材が採用される。

もちろん、DGA は非常に単純なアルゴリズムにすぎず、DGA より優れた標準アルゴリズムは他にもたくさんあります。 Maria Chiara らの 2019 年の論文「モンテカルロ アルゴリズムは、疎なランダム グラフで最大の独立セットを見つけるのに非常に効果的です」では、MIS 問題を解決するための複数のアルゴリズムのパフォーマンスについての詳細な研究が提供されています。

##これに基づいて、この研究は次のような疑問を提起します。「新しい最適化アルゴリズムを評価するとき、アルゴリズムのパフォーマンスをテストするためのベンチマークとして本当に難しい問題は何ですか?」

たとえば、この研究では、d16 の d-RRG 上の MIS を考慮します。ここで、d=20 と d=100 の結果を、2019 年の論文「モンテカルロ アルゴリズムは、疎なランダム グラフで最大の独立セットを見つけるのに非常に効果的です」で与えられた結果と比較できます。

明らかに、優れた最適化アルゴリズムは n 多項式時間で完了する必要があります。関係が線形であれば、より良いでしょう。見つかった解の品質は、単純な既存のアルゴリズムよりも優れているはずです。 . . 、n が増加しても品質は低下しないはずです。

研究の結論: 現在、ニューラル ネットワーク ベースのオプティマイザー (Martin JA Schuetz らによって提案されたオプティマイザーなど) は上記の要件を満たしておらず、単純な標準アルゴリズムと競合することはできません。難しい最適化問題を解決します。ニューラル ネットワークがこの要件を満たせるかどうか、または失敗の深い理由があるかどうかを調査することが重要です。

以上がグラフ ニューラル ネットワークは Nature サブジャーナルに掲載されましたが、通常のアルゴリズムよりも 104 倍遅いことが明らかになりました。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。