この記事は WeChat 公開アカウント「情報時代に生きる」から転載したものであり、著者は情報時代に生きています。この記事を転載するには、情報時代の暮らしの公開アカウントまでご連絡ください。
機械学習では、2 つのサンプル間の類似性とカテゴリ情報を評価できるように、2 つのサンプル間の差異をどのように判断するかが基本概念です。この類似性を判断する尺度は、特徴空間内の 2 つのサンプル間の距離です。
さまざまなデータ特性に基づいた多くの測定方法があります。一般的に、2 つのデータ サンプル x, y に対して、関数 d(x, y) を定義します。これを 2 つのサンプル間の距離として定義する場合、d(x, y) は次の基本特性を満たす必要があります。
- #非負性: d(x,y)>=0
- 恒等性: d(x,y)=0 ⇔ x=y
- 対称性: d ( x, y) = d (y, x)
- 三角不等式: d (x, y)
1. ユークリッド距離
間違いなく、ユークリッド距離は距離です。人々が最もよく知っているのは、2 点間の直線距離です。中学校の数学を学習した生徒は皆、デカルト座標系の 2 次元空間内の 2 点間の距離を計算する方法を知っています。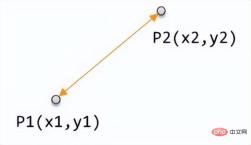
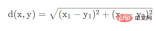
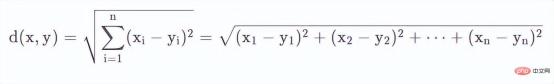
マンハッタンの距離はタクシーの距離とも呼ばれ、その概念はニューヨークのマンハッタンにある多くの水平および垂直のブロックに由来しています。近隣のタクシー運転手がある地点から別の地点まで歩きたい場合、タクシーは建物の上を飛ぶことができないため、直線距離を計算することは役に立ちません。したがって、この距離は通常、2 地点の東西および南北の距離をそれぞれ減算および加算して計算され、実際にタクシーが移動する距離となります。
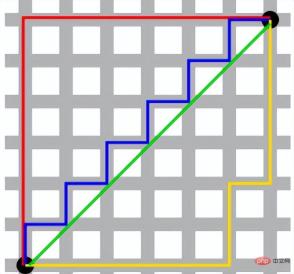 #図に示すように、赤い線と黄色の線は 2 つの異なるパスのマンハッタン距離です。数学的には、2 次元空間におけるマンハッタン距離の計算方法は次のとおりです:
#図に示すように、赤い線と黄色の線は 2 つの異なるパスのマンハッタン距離です。数学的には、2 次元空間におけるマンハッタン距離の計算方法は次のとおりです:
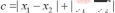
チェビシェフ距離は、2 点間の座標値の差の最大値として定義されます。
最も直感的な例はチェスのキングです。キングは横、直線、斜めに移動できますが、一度に 1 マスしか移動できないため、 move ビシェフ距離は、別のマスに移動するために必要な最小距離です。

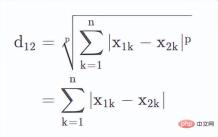
最小距離自体は特別な距離ではなく、次の式です。複数の距離 (マンハッタン距離、ユークリッド距離、チェビシェフ距離) を組み合わせます。
2 つの n 次元変数の最小距離は次のように定義されます:

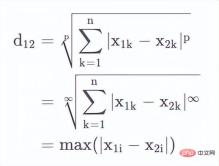
5. 標準化ユークリッド距離
ユークリッド距離は 2 点間の直線距離を測定できますが、場合によっては、異なる点の影響を受ける可能性があります。単位。例えば、身長差が5mm、体重が5kg違うと、感じ方は全く違ってくるかもしれません。 3 つのモデルをクラスタリングしたい場合、それぞれの属性は次のとおりです。 A: 65000000 mg (つまり 65 kg)、1.74 m B: 60000000 mg (つまり 60 kg) 、1.70メートル C: 65,000,000 ミリグラム (つまり 65 キログラム)、1.40 メートル 私たちの通常の理解によれば、A と B はより良い数値を持つモデルであり、同じカテゴリに分類されるべきです。しかし、実際に上記の単位で計算してみると、AとBの差の方がAとCの差よりも大きいことが分かります。その理由は、属性の測定単位が異なるため、過度の数値差が生じるためです。同じデータを別のユニットに変更した場合。 A: 65kg, 174cmB: 60kg, 170cmC: 65kg, 140cmすると、思いつく結果は、 A と B は同じカテゴリに分類されます。したがって、測定単位の違いによるこのような違いを避けるために、標準化されたユークリッド距離を導入する必要があります。この距離の計算では、各成分は平均と分散が等しい区間に正規化されます。 標本集合 X の平均 (平均) を m、標準偏差 (標準偏差) を s とすると、X の「標準化変数」は次のように表されます。 

ランス距離はキャンベラ距離とも呼ばれます、
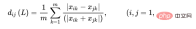
数値を統一したら問題ないでしょうか?多分。たとえば、1 次元の例では、2 つのクラスがある場合、1 つのクラスの平均は 0、分散は 0.1 で、もう 1 つのクラスの平均は 5、分散は 5 です。それでは、値が 2 の点はどのカテゴリに属すべきでしょうか?最初のカテゴリーが数値的に 2 に達する可能性は明らかに低いため、私たちは直感的にこれが 2 番目のカテゴリーであるに違いないと考えます。しかし実際には、距離から計算すると、数字の 2 は最初のカテゴリーに属さなければなりません。 したがって、分散が小さい次元では、小さな差が外れ値になる可能性があります。たとえば、下の図では、A と B は原点から同じ距離にありますが、サンプル全体が水平軸に沿って分布しているため、点 B はサンプル内の点である可能性が高く、点 A はサンプル内の点である可能性が高くなります。外れ値である可能性があります。 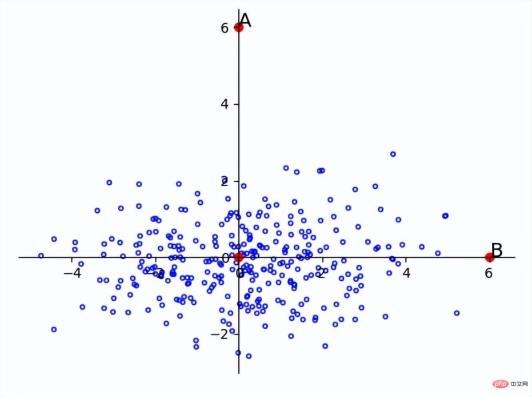
次元が独立して同一に分布していない場合にも問題が発生することがあります。たとえば、下図の点 A と点 B が原点です。は等しい距離にありますが、主分布は f(x)=x に似ているため、A は外れ値に近くなります。
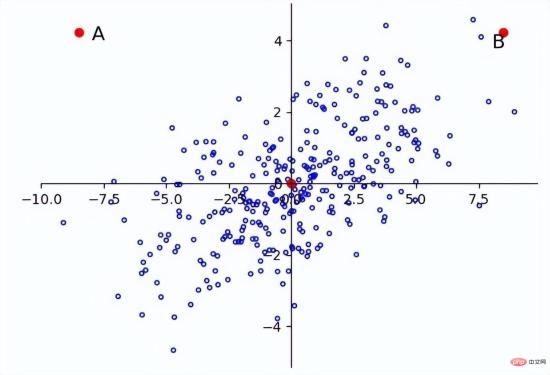
したがって、この場合、標準化ユークリッド距離にも問題があることがわかり、マハラノビス距離を導入する必要があります。
マハラノビス距離は、主成分に従って変数を回転して次元を互いに独立させた後、それらを標準化して次元が均等に分散されるようにします。主成分は固有ベクトルの方向であるため、固有ベクトルの方向に従って回転し、固有値を倍にしてスケーリングするだけで済みます。たとえば、上記の画像を変換すると、次のような結果が得られます。
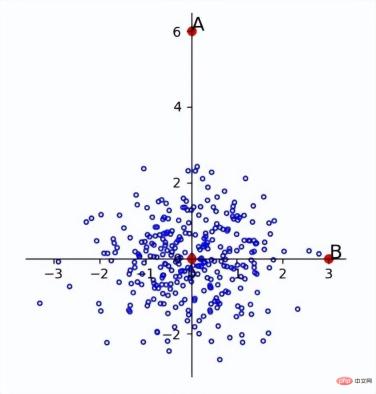
異常値が正常に分離されたことがわかります。
マハラノビス距離はインドの数学者マハラノビスによって提案され、データの共分散距離を表します。これは、2 つの未知のサンプル セットの類似性を計算する効率的な方法です。
平均

と共分散行列 Σ
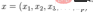 # を持つ多変量ベクトルの場合
# を持つ多変量ベクトルの場合
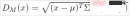
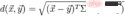
名前が示すように、コサイン距離は幾何学における角度の余弦に由来しており、方向の違いを測定するために使用できます。距離や長さではなく、2 つのベクトルの距離を表します。コサイン値が 0 の場合、2 つのベクトルは直交し、夾角は 90 度になります。角度が小さいほど、コサイン値は 1 に近づき、方向はより安定します。
N 次元空間では、コサイン距離は次のとおりです。
コサイン距離は三角不等式を満たさないことに注意してください。
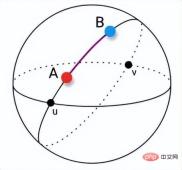
測地線距離とは、本来は球の表面間の最短距離を指します。特徴空間が平面の場合、測地線距離はユークリッド距離です。非ユークリッド幾何学では、球上の 2 点を結ぶ最短の線がその 2 点を結ぶ大弧であり、球上の三角形や多角形の辺もこの大弧で構成されます。
10. ブレイ カーティス距離
ブレイ カーティス距離は主に植物学、生態学、環境科学で使用されます。サンプル間の差異を計算するために使用されます。式は次のとおりです:
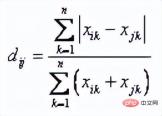
以上が機械学習に基づいた数値距離: 空間内の点間の距離の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 メタの新しいAIアシスタント:生産性ブースターまたはタイムシンク?May 01, 2025 am 11:18 AM
メタの新しいAIアシスタント:生産性ブースターまたはタイムシンク?May 01, 2025 am 11:18 AMMetaは、NVIDIA、IBM、Dellなどのパートナーと協力して、Llama Stackのエンタープライズレベルの展開統合を拡大しました。セキュリティの観点から、MetaはLlama Guard 4、Llamafirewall、Cyberseceval 4などの新しいツールを立ち上げ、AIセキュリティを強化するためにLlama Defendersプログラムを開始しました。さらに、METAは、公共サービス、ヘルスケア、教育の改善に取り組んでいる新興企業を含む、Llama Impact Grantsの150万ドルを10のグローバル機関に分配しています。 Llama 4を搭載した新しいメタAIアプリケーションは、メタAIとして考案されました
 Gen Zersの80%はAI:研究と結婚しますMay 01, 2025 am 11:17 AM
Gen Zersの80%はAI:研究と結婚しますMay 01, 2025 am 11:17 AM人間との相互作用の先駆者であるJoi Aiは、これらの進化する関係を説明するために「AI-lationships」という用語を導入しました。 Joi Aiの関係療法士であるJaime Bronsteinは、これらが人間cを置き換えることを意図していないことを明確にしています
 AIはインターネットのボット問題を悪化させています。この20億ドルのスタートアップは最前線にありますMay 01, 2025 am 11:16 AM
AIはインターネットのボット問題を悪化させています。この20億ドルのスタートアップは最前線にありますMay 01, 2025 am 11:16 AMオンライン詐欺とボット攻撃は、企業にとって大きな課題をもたらします。 小売業者は、ボットの買いだめ製品、銀行の戦闘口座の買収、ソーシャルメディアプラットフォームと戦い、なりすまし者と闘っています。 AIの台頭は、この問題を悪化させます
 ロボットへの販売:あなたのビジネスを作ったり壊したりするマーケティング革命May 01, 2025 am 11:15 AM
ロボットへの販売:あなたのビジネスを作ったり壊したりするマーケティング革命May 01, 2025 am 11:15 AMAIエージェントは、マーケティングに革命をもたらす態勢が整っており、以前の技術的変化の影響を上回る可能性があります。 これらのエージェントは、生成AIの大幅な進歩を表し、ChatGPTのような情報を処理するだけでなく、Actioも取る
 コンピュータービジョンテクノロジーがどのようにNBAプレーオフを司会しているかMay 01, 2025 am 11:14 AM
コンピュータービジョンテクノロジーがどのようにNBAプレーオフを司会しているかMay 01, 2025 am 11:14 AM重要なNBAゲーム4の決定に対するAIの影響 2つの重要なゲーム4 NBAマッチアップは、司会におけるAIのゲームを変える役割を紹介しました。 最初に、デンバーのニコラ・ジョキッチの逃した3ポインターは、アーロン・ゴードンの最後の2秒の路地につながりました。 ソニーのホー
 AIがどのように再生医療の未来を加速しているかMay 01, 2025 am 11:13 AM
AIがどのように再生医療の未来を加速しているかMay 01, 2025 am 11:13 AM伝統的に、再生医療の専門知識を拡大すると、世界的に大規模な旅行、実践的なトレーニング、長年のメンターシップが必要でした。 現在、AIはこの風景を変えており、地理的な制限を克服し、ENを通じて進歩を加速しています
 Intel Foundry Direct Connect 2025からのキーテイクアウトMay 01, 2025 am 11:12 AM
Intel Foundry Direct Connect 2025からのキーテイクアウトMay 01, 2025 am 11:12 AMIntelは、製造プロセスを主要な位置に戻すように取り組んでいますが、Fab Semiconductorの顧客を引き付けてFabでチップを作成しようとしています。この目的のために、Intelは、そのプロセスの競争力を証明するだけでなく、パートナーが馴染みのある成熟したワークフローでチップを製造できることを実証するために、業界へのより多くの信頼を築かなければなりません。今日私が聞いたことはすべて、インテルがこの目標に向かっていると信じています。 新しいCEOのタンリバイの基調講演がその日をキックオフしました。タンリバイは簡単で簡潔です。彼は、IntelのFoundry Servicesにおけるいくつかの課題と、これらの課題に対処し、将来のIntelのFoundry Servicesの成功したルートを計画するために企業が行った対策を概説しています。 Tan Libaiは、IntelのOEMサービスが顧客をより多くするために実装されているプロセスについて話しました
 AIが間違っていましたか?今、そのための保険がありますMay 01, 2025 am 11:11 AM
AIが間違っていましたか?今、そのための保険がありますMay 01, 2025 am 11:11 AMAIのリスクを取り巻く増大する懸念に対処するために、グローバルな専門家保険会社であるChaucer GroupとArmilla AIは、新しいサードパーティの責任(TPL)保険商品を導入するために力を合わせました。 このポリシーは、企業を守ります


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

SecLists
SecLists は、セキュリティ テスターの究極の相棒です。これは、セキュリティ評価中に頻繁に使用されるさまざまな種類のリストを 1 か所にまとめたものです。 SecLists は、セキュリティ テスターが必要とする可能性のあるすべてのリストを便利に提供することで、セキュリティ テストをより効率的かつ生産的にするのに役立ちます。リストの種類には、ユーザー名、パスワード、URL、ファジング ペイロード、機密データ パターン、Web シェルなどが含まれます。テスターはこのリポジトリを新しいテスト マシンにプルするだけで、必要なあらゆる種類のリストにアクセスできるようになります。

SublimeText3 中国語版
中国語版、とても使いやすい

Dreamweaver Mac版
ビジュアル Web 開発ツール

ホットトピック
 7889
7889 15
15 1650
1650 14
14 1411
1411 52
52 1302
1302 25
25 1248
1248 29
29


