翻訳者 | Li Rui
査読者 | Sun Shujuan
最適輸送は経済学から生まれ、現在はリソースを最適に割り当てる方法のツールとして開発されています。最適輸送理論の起源は、フランスの科学者ガスパール・モンジュが「地球を動かす」と称され、ナポレオン軍の要塞を構築する方法を研究した 1781 年に遡ります。全体として、最適な輸送とは、資源が移動しなければならない総距離を最小限に抑えながら、すべての資源 (鉄鉱石など) を一連の開始点 (鉱山) から一連の終了点 (製鉄所) まで移動する方法の問題です。数学的には、研究者らは、出発地とそれに対応する目的地間の総距離を最小限に抑えながら、各出発地を目的地にマッピングする関数を見つけたいと考えていました。無害な説明にもかかわらず、マンガーの概念として知られるこの問題の最初の概念の進歩は 200 年近く停滞していました。
1940 年代、ソ連の数学者レオニード カントロヴィッチは、この問題の定式化を現代版 (現在はモンジュ カントロフ理論として知られています) に修正し、これが解決への第一歩となりました。ここでの目新しさは、同じ鉱山からの一部の鉄鉱石を異なる製鉄所に供給できることです。たとえば、鉱山からの鉄鉱石の 60% を製鉄所に提供し、鉱山からの鉄鉱石の残りの 40% を別の製鉄所に提供することができます。数学的には、同じ出発地が潜在的に複数の目的地にマップされるため、これは関数ではなくなります。対照的に、これは、下図に示すように、出発地分布と目的地分布のカップリングとして知られており、青い分布(出発地)から鉱山を選択し、図に沿って垂直に移動すると、鉄鉱石がどこに送られるかが表示されます。製鉄所(目的地)。

この新しい開発の一環として、カントリヴィッチはワッサーシュタイン距離と呼ばれる重要な概念を導入しました。マップ上の 2 点間の距離と同様に、ワッサーシュタイン距離 (元のシナリオからインスピレーションを得たブルドーザー距離としても知られています) は、2 つの分布 (この場合は青とマゼンタの分布など) の間の距離を測定します。すべての鉄鉱山がすべての製鉄工場から遠い場合、鉱山の分布 (位置) と製鉄所の分布の間のワッサーシュタイン距離は大きくなります。こうした新たな改良が加えられたとしても、鉄鉱石資源を輸送する最適な方法が本当に存在するかどうか、ましてやどの方法が最適であるかは依然として不明である。最後に、1990 年代には、数学的分析と最適化の改善により問題の部分的な解決策が導き出され、理論が急速に発展し始めました。 21 世紀に入ると、最適輸送は素粒子物理学、流体力学、さらには統計学や機械学習などの他の分野にも広がり始めました。
現代における最適な交通手段
新しい理論の爆発的な増加により、最適な交通手段は、過去 20 年間にわたり、多くの新しい統計および人工知能アルゴリズムの中心となってきました。ほとんどすべての統計アルゴリズムでは、データは、明示的または暗黙的に、何らかの基礎的な確率分布を持つものとしてモデル化されます。たとえば、個人の収入に関するデータがさまざまな国で収集された場合、各国のその集団の収入の確率分布が存在します。人口の所得分布に基づいて 2 つの国を比較したい場合は、2 つの分布間のギャップを測定する方法が必要です。まさにこれが、交通手段 (特にワッサーシュタインの距離) の最適化がデータ サイエンスで非常に役立つ理由です。ただし、Wasserstein 距離は 2 つの確率分布間の距離を測る唯一の尺度ではありません。実際、物理学と情報理論との関連により、歴史的には、L-2 距離とカルバック ライブラー (KL) 発散という 2 つのオプションの方が一般的でした。これらの代替手段に対する Wasserstein 距離の主な利点は、距離を計算するときに値とその確率の両方が考慮されるのに対し、L-2 距離と KL 発散は確率のみを考慮することです。下の画像は、架空の 3 つの国の収入に関する人工データセットの例を示しています。

この場合、分布は重なり合わないため、青とマゼンタの分布の間の L-2 距離 (または KL 発散) は青とマゼンタの分布と同じになります。マゼンタの分布 緑の分布間の L-2 距離はほぼ同じです。一方、青とマゼンタの分布間のワッサーシュタイン距離は、値(水平方向の分離)間に大きな差があるため、青と緑の分布間のワッサーシュタイン距離よりもはるかに小さくなります。 Wasserstein 距離のこの特性により、分布間の差異、特にデータセット間の差異を定量化するのに理想的になります。
最適な転送による公平性の実現
毎日膨大な量のデータが収集され、多くの業界で機械学習がより一般的になっているため、データ サイエンティストは、分析とアルゴリズムを永続させないようますます注意する必要があります。データ内の既存のバイアスとバイアス。たとえば、住宅ローン承認データセットに申請者の人種に関する情報が含まれているが、使用された方法や無意識の偏見により、収集プロセスでマイノリティが差別された場合、そのデータに基づいてトレーニングされたモデルは、根本的な逸脱を反映します。
輸送を最適化すると、2 つの方法でこの偏りを軽減し、公平性を向上させることができます。最初の最も簡単な方法は、Wasserstein 距離を使用して、データセットに潜在的なバイアスがあるかどうかを判断することです。たとえば、女性に承認されたローン金額の分布と男性に承認されたローン金額の分布の間のワッサーシュタイン距離を推定できます。ワッサーシュタイン距離が非常に大きい場合、つまり統計的に有意な場合は、潜在的なバイアスが疑われる可能性があります。 2 つのグループ間に差があるかどうかを検定するこの考え方は、統計学では 2 サンプル仮説検定として知られています。
あるいは、基になるデータセット自体に偏りがある場合に、最適な配送を使用してモデルの公平性を強制することもできます。現実世界のデータセットの多くはある程度の偏りを示しており、偏りのないデータを収集するには非常に費用がかかり、時間がかかるか、実行不可能であるため、これは実用的な観点から役立ちます。したがって、たとえ不完全であっても既存のデータを使用し、モデルがこのバイアスを確実に軽減できるようにすることがより現実的です。これは、モデル予測が機密属性から統計的に独立するように強制する、強力な人口統計的パリティと呼ばれるモデル内での制約を強制することによって実現されます。 1 つのアプローチは、モデル予測の分布を、機密属性に依存しない調整された予測の分布にマッピングすることです。ただし、予測を調整するとモデルのパフォーマンスと精度も変化するため、モデルのパフォーマンスとモデルが機密属性に依存する度合い (公平性など) の間にはトレードオフが存在します。
予測の変更を最小限に抑えて最適なモデルのパフォーマンスを確保しながら、新しい予測が機密属性から独立していることを確認することで、最適な出荷を実現します。この調整されたモデルによって予測される新しい分布は、ワッサーシュタイン重心と呼ばれ、過去 10 年間にわたって多くの研究の対象となってきました。 Wasserstein の重心は、それ自体から他のすべての分布までの合計距離を最小化するという点で、確率分布の平均に似ています。下の画像は、3 つの分布 (緑、青、マゼンタ) とそのワッサーシュタインの重心 (赤) を示しています。

上記の例では、婚姻状況などの機密属性を含むデータセットに基づいて、誰かの年齢と収入を予測するモデルが構築されていると仮定します。値: 独身 (青)、既婚 (緑)、未亡人/離婚 (マゼンタ)。散布図は、さまざまな値ごとのモデル予測の分布を示します。しかし、新しいモデルの予測が人の婚姻状況を無視できるようにこれらの値を調整したい場合は、最適な輸送を使用してこれらの各分布を赤の重心にマッピングできます。すべての価値観は同じ分布にマッピングされるため、収入と年齢に基づいて人の婚姻状況を判断したり、その逆を判断したりすることはできなくなります。重心はモデルの忠実性を可能な限り維持します。
ビジネスや政府の意思決定で使用されるデータと機械学習モデルの普及が進むにつれて、これらのモデルの公正な適用を保証する方法について、新たな社会的および倫理的問題が浮上しています。多くのデータセットには、その収集方法の性質上、ある種のバイアスが含まれているため、データセットに基づいてトレーニングされたモデルがこのバイアスや歴史的差別を悪化させないことが重要です。最適な輸送は、近年増加しているこの問題を解決するための 1 つの方法にすぎません。現在では、最適な交通地図と距離を計算するための高速かつ効率的な方法があり、このアプローチは現代の大規模なデータセットに適しています。人々がデータベースのモデルや洞察にますます依存するようになるにつれ、公平性はこれまで、そして今後もデータ サイエンスの中核となる問題であり、最適な交通手段がこの目標を達成する上で重要な役割を果たすことになります。
原題: Optimal Transport and its Applications to Fairness 、著者: Terrence Alsup
以上が最適輸送とその公平性への応用の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 AIのスキルギャップは、サプライチェーンのダウンを遅くしていますApr 26, 2025 am 11:13 AM
AIのスキルギャップは、サプライチェーンのダウンを遅くしていますApr 26, 2025 am 11:13 AM「AI-Ready労働力」という用語は頻繁に使用されますが、サプライチェーン業界ではどういう意味ですか? サプライチェーン管理協会(ASCM)のCEOであるAbe Eshkenaziによると、批評家ができる専門家を意味します
 1つの会社がAIを永遠に変えるために静かに取り組んでいる方法Apr 26, 2025 am 11:12 AM
1つの会社がAIを永遠に変えるために静かに取り組んでいる方法Apr 26, 2025 am 11:12 AM分散型AI革命は静かに勢いを増しています。 今週の金曜日、テキサス州オースティンでは、ビテンサーのエンドゲームサミットは極めて重要な瞬間を示し、理論から実用的な応用に分散したAI(DEAI)を移行します。 派手なコマーシャルとは異なり
 Nvidiaは、AIエージェント開発を合理化するためにNEMOマイクロサービスをリリースしますApr 26, 2025 am 11:11 AM
Nvidiaは、AIエージェント開発を合理化するためにNEMOマイクロサービスをリリースしますApr 26, 2025 am 11:11 AMエンタープライズAIはデータ統合の課題に直面しています エンタープライズAIの適用は、ビジネスデータを継続的に学習することで正確性と実用性を維持できるシステムを構築する大きな課題に直面しています。 NEMOマイクロサービスは、NVIDIAが「データフライホイール」と呼んでいるものを作成することにより、この問題を解決し、AIシステムがエンタープライズ情報とユーザーインタラクションへの継続的な露出を通じて関連性を維持できるようにします。 この新しく発売されたツールキットには、5つの重要なマイクロサービスが含まれています。 NEMOカスタマイザーは、より高いトレーニングスループットを備えた大規模な言語モデルの微調整を処理します。 NEMO評価者は、カスタムベンチマークのAIモデルの簡素化された評価を提供します。 Nemo Guardrailsは、コンプライアンスと適切性を維持するためにセキュリティ管理を実装しています
 aiは芸術とデザインの未来のために新しい絵を描きますApr 26, 2025 am 11:10 AM
aiは芸術とデザインの未来のために新しい絵を描きますApr 26, 2025 am 11:10 AMAI:芸術とデザインの未来 人工知能(AI)は、前例のない方法で芸術とデザインの分野を変えており、その影響はもはやアマチュアに限定されませんが、より深く影響を与えています。 AIによって生成されたアートワークとデザインスキームは、広告、ソーシャルメディアの画像生成、Webデザインなど、多くのトランザクションデザインアクティビティで従来の素材画像とデザイナーに迅速に置き換えられています。 ただし、プロのアーティストやデザイナーもAIの実用的な価値を見つけています。 AIを補助ツールとして使用して、新しい美的可能性を探求し、さまざまなスタイルをブレンドし、新しい視覚効果を作成します。 AIは、アーティストやデザイナーが繰り返しタスクを自動化し、さまざまなデザイン要素を提案し、創造的な入力を提供するのを支援します。 AIはスタイル転送をサポートします。これは、画像のスタイルを適用することです
 エージェントAIとのズームがどのように革命を起こしているか:会議からマイルストーンまでApr 26, 2025 am 11:09 AM
エージェントAIとのズームがどのように革命を起こしているか:会議からマイルストーンまでApr 26, 2025 am 11:09 AM最初はビデオ会議プラットフォームで知られていたZoomは、エージェントAIの革新的な使用で職場革命をリードしています。 ZoomのCTOであるXD Huangとの最近の会話は、同社の野心的なビジョンを明らかにしました。 エージェントAIの定義 huang d
 大学に対する実存的な脅威Apr 26, 2025 am 11:08 AM
大学に対する実存的な脅威Apr 26, 2025 am 11:08 AMAIは教育に革命をもたらしますか? この質問は、教育者と利害関係者の間で深刻な反省を促しています。 AIの教育への統合は、機会と課題の両方をもたらします。 Tech Edvocate NotesのMatthew Lynch、Universitとして
 プロトタイプ:アメリカの科学者は海外の仕事を探していますApr 26, 2025 am 11:07 AM
プロトタイプ:アメリカの科学者は海外の仕事を探していますApr 26, 2025 am 11:07 AM米国における科学的研究と技術の開発は、おそらく予算削減のために課題に直面する可能性があります。 Natureによると、海外の雇用を申請するアメリカの科学者の数は、2024年の同じ期間と比較して、2025年1月から3月まで32%増加しました。以前の世論調査では、調査した研究者の75%がヨーロッパとカナダでの仕事の検索を検討していることが示されました。 NIHとNSFの助成金は過去数か月で終了し、NIHの新しい助成金は今年約23億ドル減少し、3分の1近く減少しました。リークされた予算の提案は、トランプ政権が科学機関の予算を急激に削減していることを検討しており、最大50%の削減の可能性があることを示しています。 基礎研究の分野での混乱は、米国の主要な利点の1つである海外の才能を引き付けることにも影響を与えています。 35
 オープンAIの最新のGPT 4.1ファミリ - 分析VidhyaApr 26, 2025 am 10:19 AM
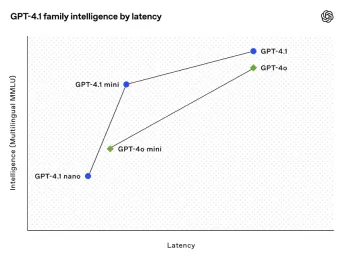
オープンAIの最新のGPT 4.1ファミリ - 分析VidhyaApr 26, 2025 am 10:19 AMOpenaiは、強力なGPT-4.1シリーズを発表しました。実際のアプリケーション向けに設計された3つの高度な言語モデルのファミリー。 この大幅な飛躍は、より速い応答時間、理解の強化、およびTと比較した大幅に削減されたコストを提供します


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

AtomエディタMac版ダウンロード
最も人気のあるオープンソースエディター

MantisBT
Mantis は、製品の欠陥追跡を支援するために設計された、導入が簡単な Web ベースの欠陥追跡ツールです。 PHP、MySQL、Web サーバーが必要です。デモおよびホスティング サービスをチェックしてください。

DVWA
Damn Vulnerable Web App (DVWA) は、非常に脆弱な PHP/MySQL Web アプリケーションです。その主な目的は、セキュリティ専門家が法的環境でスキルとツールをテストするのに役立ち、Web 開発者が Web アプリケーションを保護するプロセスをより深く理解できるようにし、教師/生徒が教室環境で Web アプリケーションを教え/学習できるようにすることです。安全。 DVWA の目標は、シンプルでわかりやすいインターフェイスを通じて、さまざまな難易度で最も一般的な Web 脆弱性のいくつかを実践することです。このソフトウェアは、

WebStorm Mac版
便利なJavaScript開発ツール

SAP NetWeaver Server Adapter for Eclipse
Eclipse を SAP NetWeaver アプリケーション サーバーと統合します。

ホットトピック
 7748
7748 15
15 1643
1643 14
14 1397
1397 52
52 1291
1291 25
25 1234
1234 29
29



