ホームページ >テクノロジー周辺機器 >AI >拡散モデルの背後にある数学は難しすぎて理解しにくいですか? Google は統一された視点でそれを明確にします
拡散モデルの背後にある数学は難しすぎて理解しにくいですか? Google は統一された視点でそれを明確にします
- 王林転載
- 2023-04-11 19:46:081314ブラウズ
最近、AIペイントがとても人気があります。
AI の描画機能に驚嘆する一方で、拡散モデルが AI において大きな役割を果たしているということはご存じないかもしれません。人気モデルOpenAIのDALL・E 2を例に挙げると、簡単なテキスト(プロンプト)を入力するだけで、1024*1024の高解像度画像を複数生成できます。
DALL・E 2 が発表されて間もなく、Google は、指定されたテキストの説明からシーンのリアルな画像を生成できるテキストから画像への AI モデルである Imagen をリリースしました。 。
ほんの数日前、Stability.Ai はテキスト生成画像モデル Stable Diffusion の最新バージョンを公開し、生成された画像は商用グレードに達しました。
Google が 2020 年に DDPM をリリースして以来、普及モデルは徐々に発電分野で新たな注目のスポットになりました。その後、OpenAI が GLIDE や ADM-G モデルなどを発表し、普及モデルが普及しました。
多くの研究者は、拡散モデルに基づくテキスト画像生成モデルはパラメータが少ないだけでなく、より高品質な画像を生成し、GAN に代わる可能性があると考えています。
しかし、拡散モデルの背後にある数式は、VAE や GAN よりも理解するのがはるかに難しいと多くの研究者が信じており、多くの研究者を落胆させています。
最近、Google Research の研究者が「拡散モデルを理解する: 統一された視点」を執筆しました。この記事では、拡散モデルの背後にある数学的原理を非常に詳細に示しており、他の人にも理解してもらえるようにすることを目的としています。研究者は、拡散モデルとは何か、そしてそれがどのように機能するのかを追跡して学ぶことができます。 
論文アドレス: https://arxiv.org/pdf/2208.11970.pdf この論文がどれほど「数学的」であるかについて、論文の著者は次のように述べています。それは次のようになります: これらのモデルの背後にある数学を、耐え難いほど詳細に示します。
この論文は 6 つの部分に分かれており、主に生成モデル、ELBO、VAE、階層型 VAE、変分拡散モデル、スコアベースの生成モデルなどが含まれます。

以下は、紹介用の論文からの抜粋です:
世代モデル
分布内の観測サンプル x が与えられた場合、生成モデルの目標は、その真のデータ分布 p(x) をモデル化する方法を学習することです。モデルが学習された後、新しいサンプルを生成できます。さらに、いくつかの形式では、学習モデルを使用して観測値やサンプルデータを評価することもできます。
現在の研究文献には、いくつかの重要な方向性があります。この記事では、主に次のようなものを含む、高レベルで簡単に紹介するだけです: 複雑な分布のサンプリング プロセスをモデル化する GAN。 。 「尤度ベースの」手法とも呼ばれる生成モデルは、観察されたデータ サンプルに高い尤度を割り当てることができ、通常は自己回帰、正規化されたフロー、VAE を含みます。エネルギーベースのモデリング。このアプローチでは、分布は任意の柔軟なエネルギー関数として学習され、その後正規化されます。スコアベースの生成モデルでは、エネルギー関数自体をモデル化することを学習するのではなく、エネルギー モデルに基づくスコアがニューラル ネットワークとして学習されます。
この研究では、この論文で示されているように、拡散モデルには尤度ベースの解釈とスコアベースの解釈があることを調査してレビューします。
変分拡散モデル
簡単に見ると、変分拡散モデル (VDM) には 3 つの主要な制限された (または仮定された) マルコフがあると考えることができます。階層変分オートエンコーダ (MHVAE)、それらは次のとおりです:
- 潜在次元はデータ次元とまったく同じです;
- 各タイム ステップにおける潜在エンコーダーの構造は学習されず、事前定義されます線形ガウスモデルとして。言い換えれば、これは前のタイム ステップの出力を中心としたガウス分布です。
- #ポテンシャル エンコーダーのガウス パラメーターは時間の経過とともに変化し、ポテンシャル分布の基準は時間の経過とともに変化します。プロセスの最終時間ステップ T はガウス分布です。
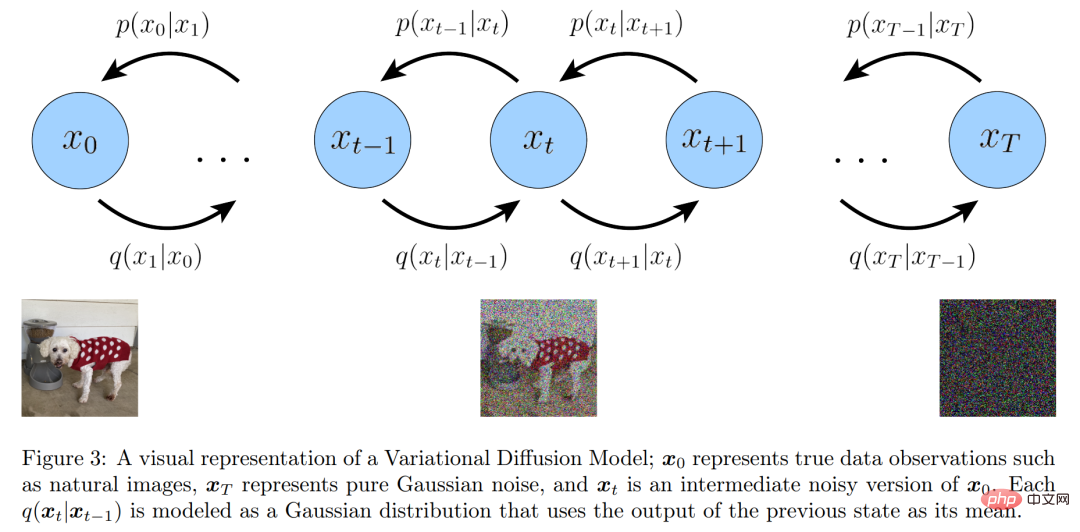
#変分拡散モデルの視覚的表現
さらに、標準マルコフ階層変分オートエンコーダーからの階層変換間のマルコフ プロパティを明示的に維持します。彼らは、上記の 3 つの主要な仮定の意味を 1 つずつ拡張しました。
最初の仮定から始めると、シンボルの誤用により、実データ サンプルと潜在変数は x_t として表現できるようになりました。ここで、t=0 は実サンプル データを表し、t ∈ [1 , T] は対応する潜在変数を表し、その階層構造は t によってインデックス付けされます。 VDM 事後分布は MHVAE 事後分布と同じですが、次のように書き換えることができます:

2 番目の仮説より, エンコーダーにおける各潜在変数の分布は、以前に層化された潜在変数を中心としたガウス分布であることが知られています。 MHVAE とは異なり、各タイム ステップでのエンコーダーの構造は学習されず、線形ガウス モデルとして固定されます。平均と標準偏差はハイパーパラメーターとして事前設定することも、パラメーターとして学習することもできます。数学的には、エンコーダ変換は次のように表されます。
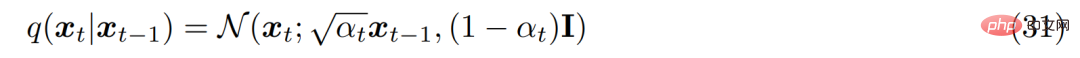
#3 番目の仮説の場合、α_t は固定されるか、次に従って学習可能です。取得されたスケジュールは時間の経過とともに進化するため、最終的な潜在変数 p(x_T) の分布は標準ガウス分布になります。その後、MHVAE の結合分布を更新でき、VDM の結合分布は次のように記述できます。一般に、この一連の仮定は、時間の経過とともに変化する画像の安定したノイズを説明します。研究者らは、ガウス ノイズを追加することで画像を徐々に破損させ、最終的にはガウス ノイズと同一になりました。
他の HVACE と同様に、VDM は証拠下限 (ELBO) を最大化することで最適化できます。これは次のように導出されます。 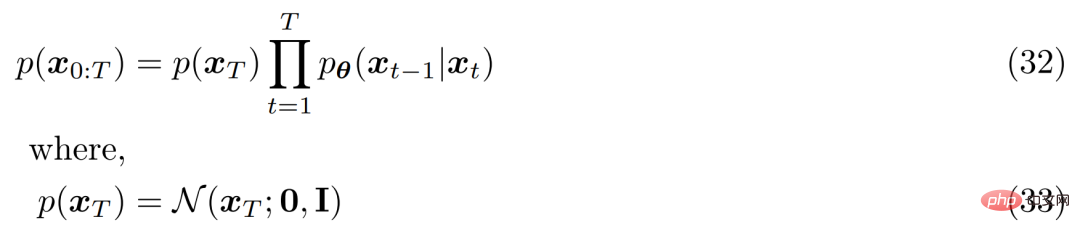
#ELBO の説明プロセスを以下の図 4 に示します。
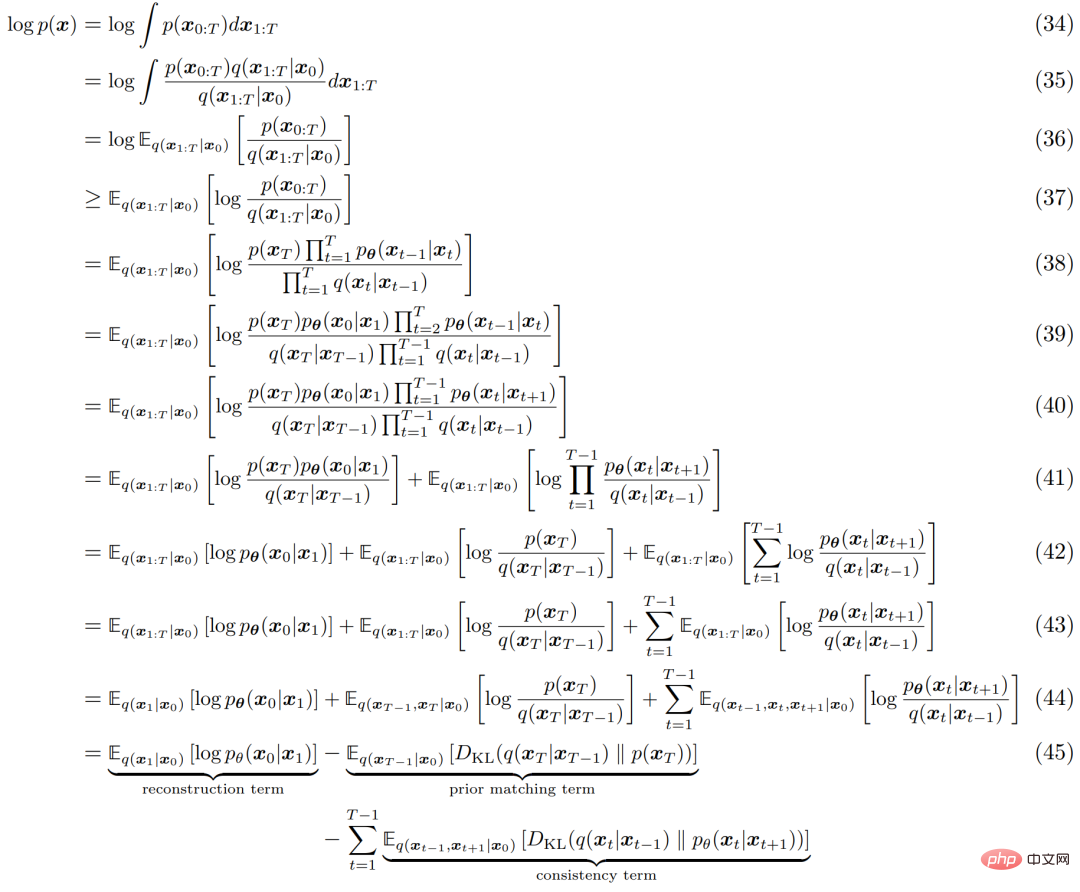 # #3 つの等価な説明
# #3 つの等価な説明
#前に示したように、変分拡散モデルは、任意のノイズのあるバージョン x_t とその時間インデックス t 自然画像 x_0 から元の x_t を予測するニューラル ネットワークを学習するだけでトレーニングできます。ただし、x_0 には同等のパラメータ化が 2 つあり、VDM のさらに 2 つの解釈を開発できます。
まず、大量のパラメータ化手法を使用できます。 q(x_t|x_0) の形式を導出する場合、式 69 は次のように整理できます。 これを、以前に導出された真のノイズ除去変換平均 µ_q(x_t, x_0) に取り込むと、次のように再導出できます。近似のノイズ除去変換平均 µ_θ(x_t, t) は次のように設定されます:
対応する最適化問題は次のようになります。 :
変分拡散モデルの 3 つの一般的な解釈を導き出すには、Tweedie の公式に目を向ける必要があります。これは、サンプルが与えられた場合、指数関数的家族分布の真の平均は、サンプルの最尤推定値 (経験的平均とも呼ばれる) に推定スコアを含む補正項を加えたものによって推定できることを指します。 数学的に言えば、ガウス変数 z 〜 N (z; µ_z, Σ_z) の場合、トゥイーディー公式は次のように表されます。 スコアベースの生成モデル 幸いなことに、この直感は、別のタイプの生成モデル、つまりスコアベースの生成モデルの助けを借りて得ることができます。実際、研究者らは、以前に導出された VDM 定式化が同等の分数ベースの生成モデリング定式化を持ち、2 つの解釈の間で柔軟な切り替えが可能であることを実証しました。 スコア関数の最適化がなぜ意味があるのかを理解するために、研究者らはエネルギーベースのモデルを再検討しました。任意の柔軟な確率分布は次のように記述できます。
正規化定数の計算またはモデル化を回避する方法。その方法は次のとおりです。ニューラル ネットワーク s_θ(x) を使用して、分布 p(x) のスコア関数 ∇ log p(x) を学習します。式 152 の両辺は対数微分できることがわかります:
# これはニューラル ネットワークとして自由に表現できます。 、正規化定数は含まれません。スコア関数は、トゥルー スコア関数を使用してフィッシャーの発散を最小限に抑えることで最適化できます。
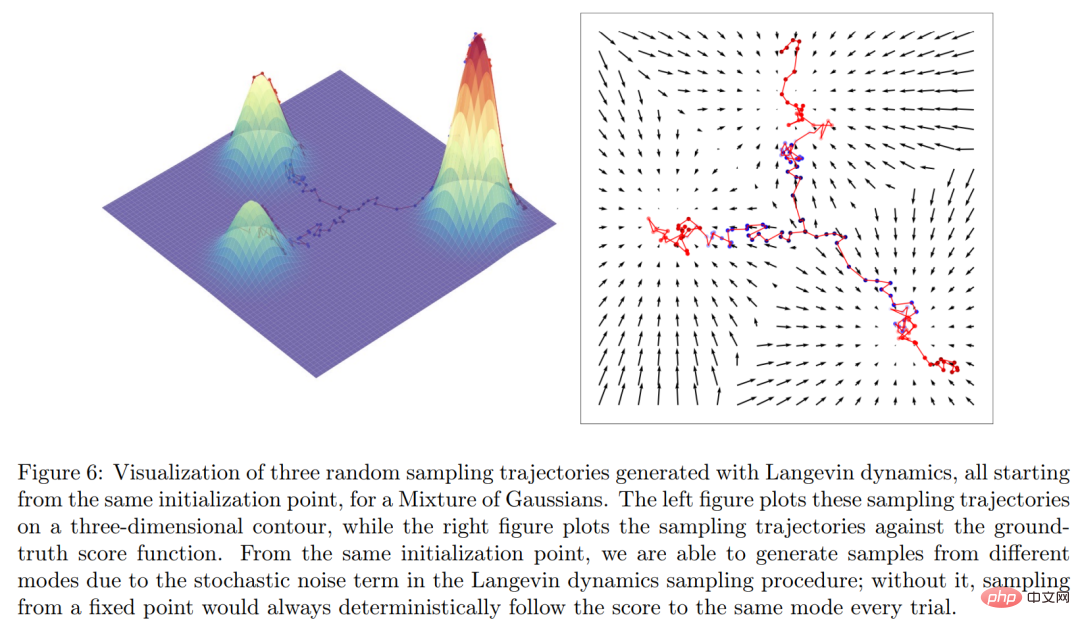
直観的に言えば、スコア関数はデータ x が位置する空間全体にわたるベクトル場を定義します。モデルは以下の図 6 に示されています。
最後に、研究者らは変分拡散モデルとスコアベースのモデル間の明示的な関係の生成を確立しました。 詳細については、元の論文を参照してください。 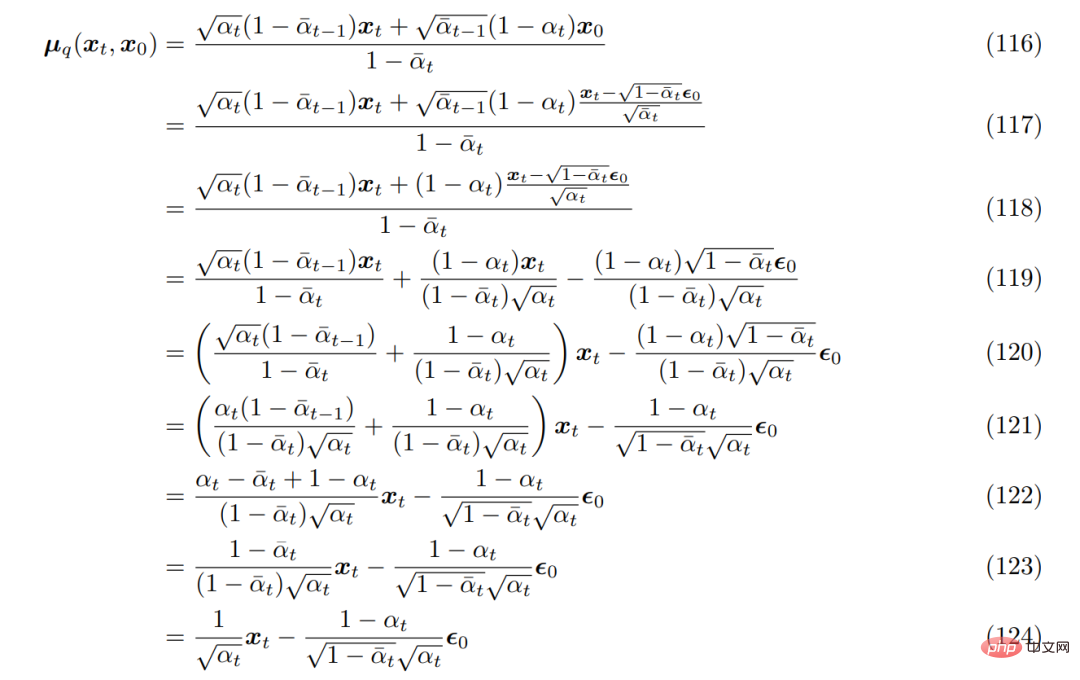
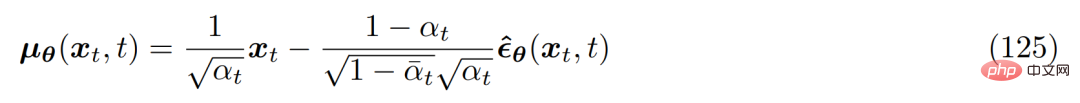
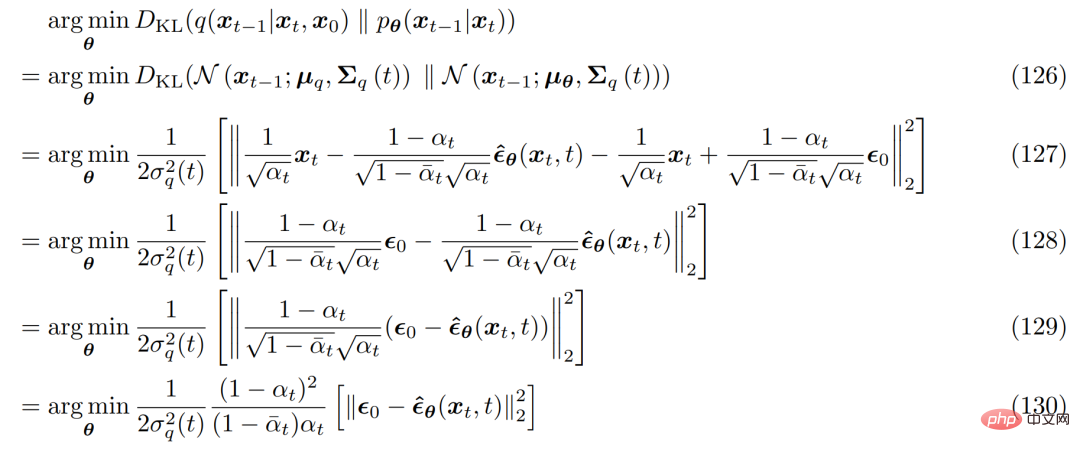
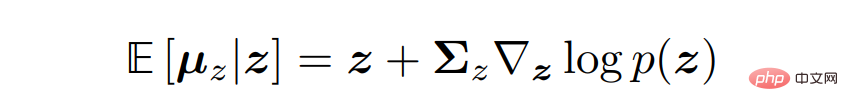 研究者らは、ニューラル ネットワークを最適化するだけで変分拡散モデルを学習できることを示しました。s_θ(x_t, t) が得られます。スコア関数 ∇ log p(x_t) を予測します。ただし、導出におけるスコア項は、Tweedie の公式の適用から得られます。これは、スコア関数が正確に何であるか、またはそれがモデル化する価値がある理由について、必ずしも優れた直観や洞察を提供するとは限りません。
研究者らは、ニューラル ネットワークを最適化するだけで変分拡散モデルを学習できることを示しました。s_θ(x_t, t) が得られます。スコア関数 ∇ log p(x_t) を予測します。ただし、導出におけるスコア項は、Tweedie の公式の適用から得られます。これは、スコア関数が正確に何であるか、またはそれがモデル化する価値がある理由について、必ずしも優れた直観や洞察を提供するとは限りません。 
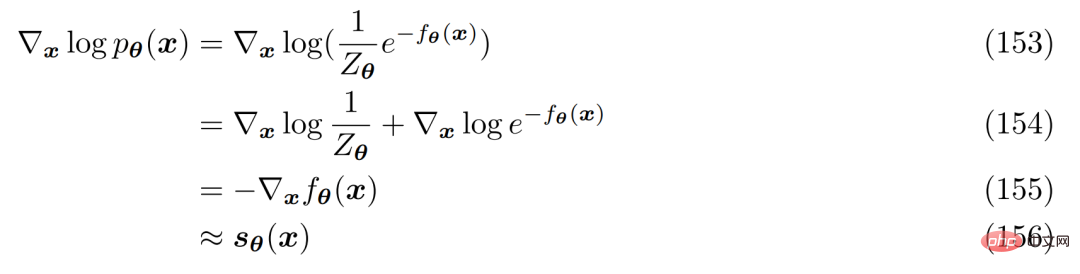

以上が拡散モデルの背後にある数学は難しすぎて理解しにくいですか? Google は統一された視点でそれを明確にしますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

