ホームページ >テクノロジー周辺機器 >AI >因果推論でデータをより有効に活用するにはどうすればよいでしょうか?
因果推論でデータをより有効に活用するにはどうすればよいでしょうか?
- PHPz転載
- 2023-04-11 19:43:021596ブラウズ

はじめに: この共有のタイトルは、「因果推論でデータをより有効に活用するには?」です。 」 」では、因果関係に関する出版論文に関連したチームの最近の研究を主に紹介します。本レポートでは、より多くのデータを活用して因果推論を行う方法を、履歴管理データを活用して明示的に混乱バイアスを軽減する方法と、複数ソースデータの融合による因果推論の2つの側面から紹介します。
#全文目次:
- #因果推論の背景
- 修正因果ツリー GBCT
- 因果データ融合
- Ant のビジネス アプリケーションの場合
機械学習の一般的な予測問題たとえば、喫煙者の肺がんの確率の予測、画像の分類、その他の予測問題などでは、通常、独立した同一の分布が想定されます。因果関係の問題は、データの背後にあるメカニズムに関係します。「喫煙は肺がんの原因になりますか?」などのよくある質問も同様の質問です。
因果効果推定の問題では、非常に重要な 2 つのタイプのデータがあります。1 つのタイプは観測データで、もう 1 つのタイプはランダム化によって生成された実験データです。管理された実験です。
- #観測データは、私たちの実際の生活や製品の中で蓄積されたデータです。たとえば、喫煙データは喫煙を好む人がいることを示していますが、観察データは喫煙者に関するものであり、最終的には喫煙者の中にはがんになる人もいます。機械学習の予測問題は、条件付き確率 P (肺がんになる | 喫煙)、つまり、喫煙条件が与えられた場合に、喫煙者が肺がんになる確率を推定することです。上記の観察データでは、喫煙の分布は実際にはランダムではありません。喫煙に対する好みは人それぞれ異なり、環境にも影響されます。
- #因果関係の質問に答える最良の方法は、ランダム化比較実験を実施することです。実験データは、ランダム化対照実験を通じて取得されます。ランダム化比較試験では、治療への割り当てはランダムです。 「喫煙が肺がんの原因となるかどうか」という結論を得るために実験を行う必要があるとします。まず、十分な数の人々を見つけ、そのうちの半数には喫煙を強制し、残りの半数には禁煙を強制し、肺がんの発生確率を観察する必要があります。 2つのグループに分けられるがん。倫理やポリシーなどの要因により、一部のシナリオではランダム化比較試験は不可能ですが、検索プロモーションにおける A/B テストなど、一部の分野ではランダム化比較試験を引き続き実施できます。
 #因果推定問題 E(Y|do(X)) 問題と従来の予測または分類問題 E(Y|X) の主な違いは、Judy Pearl によって提案された介入シンボル do が与えられた条件で現れることです。介入して X 変数を特定の値に強制します。本報告書における因果関係の推定とは、主に観測データから因果関係を推定することを指します。
#因果推定問題 E(Y|do(X)) 問題と従来の予測または分類問題 E(Y|X) の主な違いは、Judy Pearl によって提案された介入シンボル do が与えられた条件で現れることです。介入して X 変数を特定の値に強制します。本報告書における因果関係の推定とは、主に観測データから因果関係を推定することを指します。
#因果推論でデータをより効果的に活用するにはどうすればよいでしょうか?本レポートでは、このようなトピックについて、2つのチームが発表した最近の論文を例に紹介します。
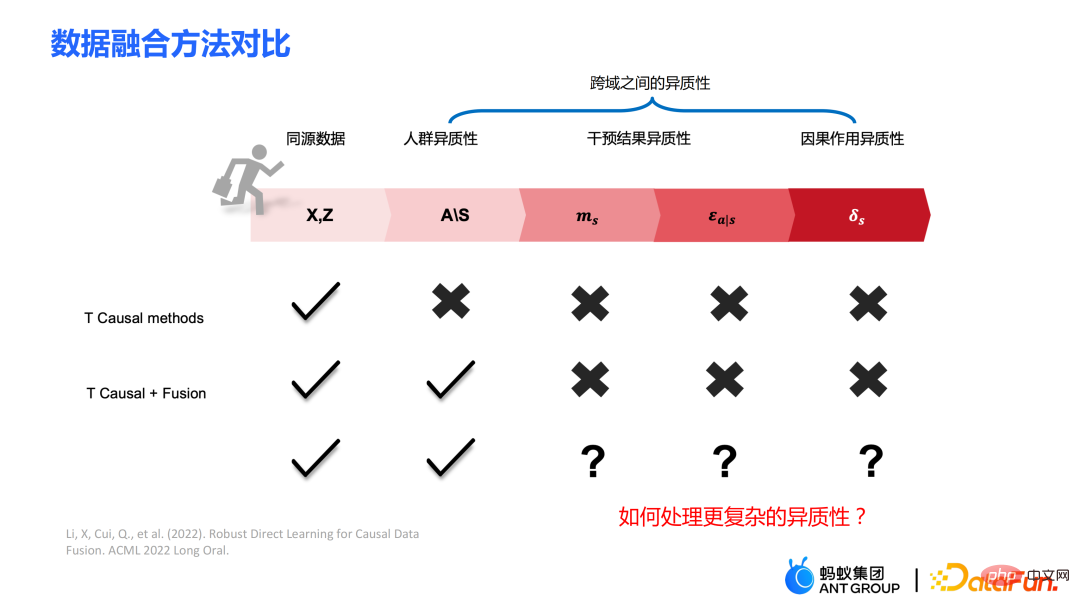
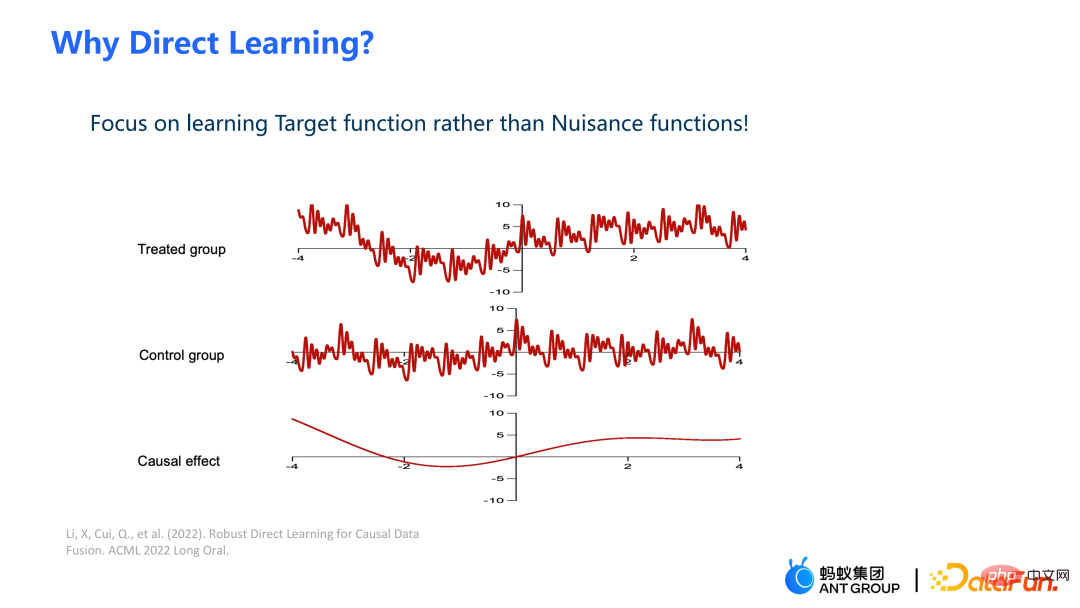
従来の因果ツリー アルゴリズムの中には、因果効果の不均一性に基づいて分割されているものがあります。データ分布における因果関係の不均一性。 因果ツリーでは、子ノードが分割されて得られますが、分割されて得られた左の子ノードと右の子ノードの分布が均一になることは保証できるでしょうか? 従来の因果ツリーと隆起ツリーでは、左側を保証できません分割後、子ノードと右側の子ノードの分布は均一になります。したがって、前のセクションで説明した従来の推定 私たちの研究は、実験グループ (治療グループ) に対する平均因果効果 CATT を推定することに焦点を当てています。 CATT は次のように定義されます: ##さらに、従来の因果効果推定は 2 つの部分に分割できます: 選択バイアス/交絡バイアスは次のように定義できます: ##直観的な意味は、実験グループの治療 = 0 の場合の推定値から、対照グループの治療 = 0 の場合の推定値を引いたものです。従来の因果関係ツリーでは、上記のバイアスは特徴づけられておらず、選択バイアスが推定値に影響を及ぼし、最終的な推定値にバイアスがかかる可能性があります。 直観的な意味は次のとおりです。実験グループでは、対照グループのモデルを使用します。推定; 対照群では、推定に実験群のモデルを使用します; 実験群と対照群の分布が可能な限り同じになるように、2 つの部分の推定値を可能な限り近づけます。混乱エントロピーの使用は、私たちの研究の主な貢献の 1 つです。 #従来のツリー モデルの統合には、バギングやブースティングなどの方法が含まれます。隆起フォレストと因果フォレストの統合方法はバギング法であり、隆起フォレストの統合は直接加算ですが、因果フォレストの統合は損失関数を解く必要があります。 # GBCT で設計された明示的補正モジュールにより、GBCT はブースティング手法を使用した積分をサポートします。基本的な考え方はブースティングと似ています。最初のツリーが修正された後、2 番目のツリーが修正され、3 番目のツリーが修正されます... 実験は 2 つの部分で行われました: グラウンド トゥルースを含むシミュレーション実験で、GBCT 法が期待される結果を達成できるかどうかをテストします。シミュレーション実験のデータ生成は 2 つの部分に分かれています (表の最初の列 Φ は選択バイアスを表します。Φ 値が大きいほど、対応する選択バイアスが強くなります。表内の値は MAE です。MAE 値が小さいほど、 、方法が優れているほど) : 。ランダム化比較実験が実施され、ランダム化比較実験に基づいて偏ったデータが構築されました。 GBCT 手法は、さまざまな設定にわたって一貫して従来の手法より優れたパフォーマンスを示し、特に偏ったデータに対しては従来の手法よりも大幅に優れたパフォーマンスを発揮します。 2 番目のタスクは因果データの融合、つまり因果効果をより適切に推定する方法です。 #主なシンボル: 複数のデータ ソース、Y は結果、A は治療、X は懸念事項の関連性 変数、 Z は X を除く各データ ソース (ドメイン) の他の共変量、S はどのドメインに属するかを示すために使用されるドメインの指標、μ は潜在的な結果の期待値です。結果を次の式に分解します。 ##ターゲット関数 δ は、各ドメインに対する因果関係を推定するために使用されます。 、迷惑関数には、主効果、傾向スコア、ドメイン傾向スコア、効果の分散などが含まれます。 メタ学習器などの一部の従来の手法は、データの起源が同じであることを前提としています。つまり、分布は一貫しています。一部の従来のデータ融合手法は、ドメイン間の集団の異質性を処理できますが、ドメイン間の介入結果や因果関係の異質性を明示的に捉えることはできません。私たちの研究は、介入結果におけるドメイン間の異質性や因果関係におけるドメイン間の異質性など、ドメイン間のより複雑な異質性への対処に焦点を当てています。 #クロスドメイン異質性のさまざまな程度を特徴付ける方法 左の部分では、因果関係が複数のドメイン間で同じであると仮定していますが、結果は不均一である可能性があります。右側は、各ドメイン間の因果効果が異なる、つまり、異なるドメイン間では、その共変量が同じであっても、その因果効果も異なると仮定しています。 式は分解式に基づいて導出され、結果 Y から主効果を引いたものを治療で割ったものが I(X) と推定され、得られる最適解は δ(X) となります。 この作業には 3 つの利点があります: ① さまざまな設計を通じて、介入結果の不均一性を処理できるだけでなく、因果関係間の不均質性; ② 二重の堅牢性の特性を持っています。論文では、ドメインの傾向スコア モデルまたは主効果モデルの推定値に偏りがない限り、最終的な推定値にも偏りがないことが証明されています (実際の状況はもう少し複雑です。詳細については論文を参照してください)。 ; #③ この作業では、主にセミパラメトリック モデルのフレームワークを設計しました。モデルの各モジュールは任意の機械学習モデルを使用でき、モデル全体をニューラル ネットワークに設計してエンドツーエンドの学習を実現することもできます。 #Weighting のモジュールは、統計学の効率限界理論に基づいています。これには主に 2 つの側面の情報が含まれています: ① #③ V を使用して、データ内のノイズを特徴付けます。ノイズは分母にあるため、ノイズが少ないサンプルの重みは大きくなります。 上記の 3 つの部分を巧みに組み合わせることで、異なるドメイン間の分布の違いと異なる因果情報のパフォーマンスを、統一されたドメインにマッピングできます。
4. Ant のビジネス アプリケーション 金融信用リスク管理シナリオでは、割当量の増加や価格引き下げなどの介入手法により、残高やリスクの変化などの期待される効果が達成されることが期待されます。いくつかの実際のシナリオでは、GBCT の矯正作業は、額リフト前の期間の履歴パフォーマンス (額リフトを行わない実験グループと対照グループの状態を取得できます) を使用し、履歴情報を通じて明示的な矯正を実行します。そのため、介入後の推定値がより正確になります。介入前の行動が揃うように GBCT が子ノードに分割されると、介入後の因果効果の推定が容易になります。 (修正後) 図中、赤色が額上げ群、青色が額上げなし群、中央の灰色の部分が推定因果効果である。 GBCT は、より適切なインテリジェントな意思決定を行い、クレジット商品のバランスとリスクを管理するのに役立ちます。 A1: GBCT 補正の主なアイデアは、履歴比較情報を使用して選択バイアスを明示的に低減することです。GBCT 法と DID 二重差分法には類似点と相違点があります。 : A2: すべての交絡変数が観察された場合、無視可能性の仮定はある程度満たされますが、選択バイアスは明示的に減少しませんが、実験はまた、従来の方法でグループとコントロール グループの整合性を達成することは可能であり、実験では GBCT のパフォーマンスがわずかに優れており、明示的な補正により結果がより安定していることが示されています。 観測されていない交絡変数がいくつかあると仮定します。この種のシナリオは、実際には非常に一般的です。観測されていない交絡変数は、履歴管理データにも存在します。変数:割り当てが引き上げられる前の家族状況や収入の変化は観察できない可能性がありますが、ユーザーの経済行動は過去のデータに反映されています。私たちは、過去のパフォーマンス情報による混同エントロピーなどの方法を通じて選択バイアスを明示的に削減し、ツリーが分割されたときに交絡変数間の異質性を分割された子ノードに特徴付けることができるようにしたいと考えています。子ノードの中で、観測されていない交絡変数は比較的近いため確率が高く、推定される因果効果は比較的正確になります。 #A3: 比較が行われました。ダブル機械学習はセミパラメトリック手法です。この記事での作業はツリーベースのメソッドに重点を置いているため、選択される基本学習器はツリーまたはフォレスト関連のメソッドです。表内の DML-RF は、ランダム フォレストの Double Machine Learning バージョンです。 #DML と比較して、GBCT は主に履歴比較データの使用方法を考慮します。比較方法では、履歴結果が共変量として直接処理されますが、この処理方法では明らかに情報が有効に活用されていません。 #A4: この問題は金融の現場において非常に本質的な問題です。検索プロモーションでは、オフラインとオンラインの違いは、オンライン学習や A/B テストを通じて部分的に克服できます。金融シナリオでは、政策の影響によりオンラインで実験を行うのは容易ではなく、また、パフォーマンスの観察期間も通常より長くなり、例えばクレジット商品の場合、ユーザーのフィードバックを観察するには少なくとも1か月かかります。したがって、この問題を完全に解決することは実際には非常に困難です。 当社では通常、オフライン評価時の検証にさまざまな期間 (OOT) のテスト データを使用し、そのパフォーマンスの堅牢性を観察するというアプローチを採用しています。テストのパフォーマンスが比較的安定している場合、オンラインのパフォーマンスも良好であると信じる理由が比較的多くなります。
#2. 修正原因と結果ツリー GBCT
1. 従来の原因と結果ツリー
ツリー アルゴリズムは主に 2 つのモジュールで構成されます:
一般的なパラメータ推定方法は、因果関係の推定値として、分割リーフ ノード上の対照グループの平均結果から実験グループの平均結果を直接差し引くことです。効果と値ランダム化比較実験の場合、治療の配分メカニズムはランダムであり、そこから計算された平均差が因果効果となります。ランダム割り当てメカニズムにより、実験グループと対照グループのデータ分布が同じになることが保証されます。これは均一性と呼ばれます。
2. 補正因果ツリー GBCT
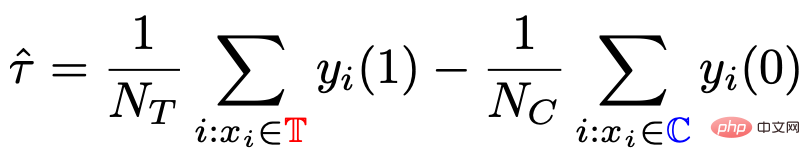 # にはバイアスがかかっています。
# にはバイアスがかかっています。 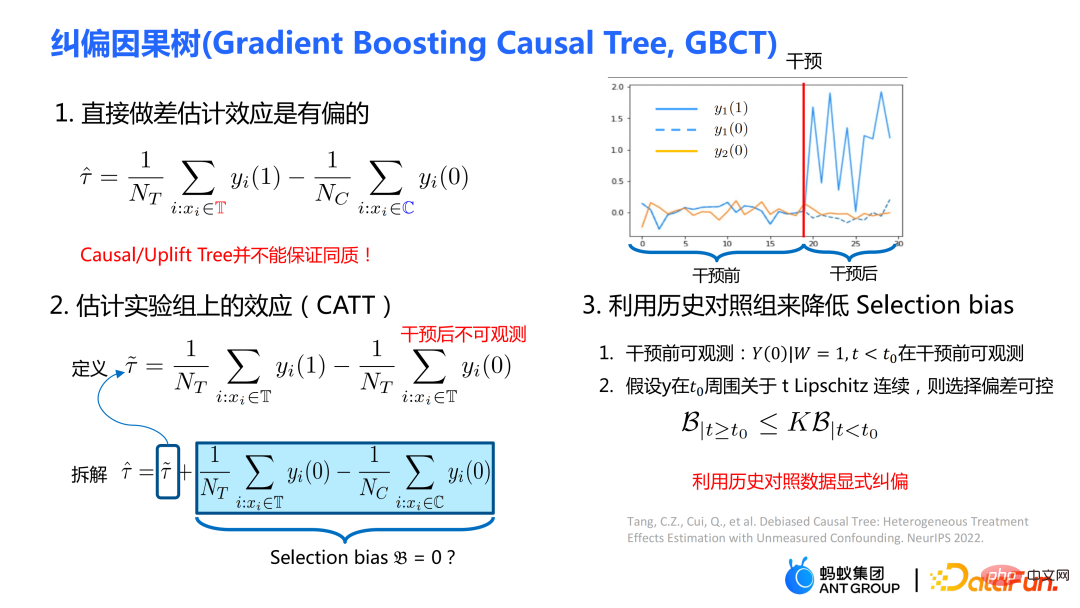
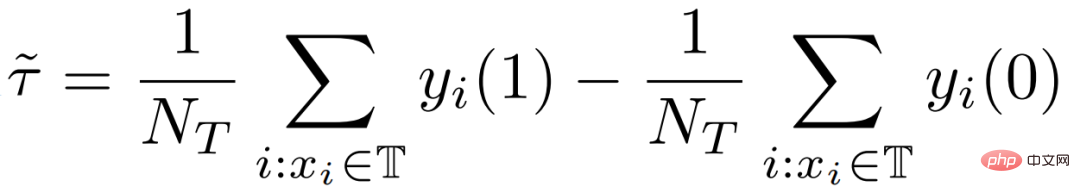
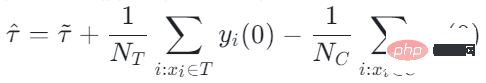
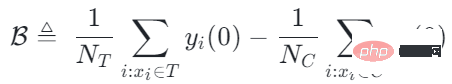
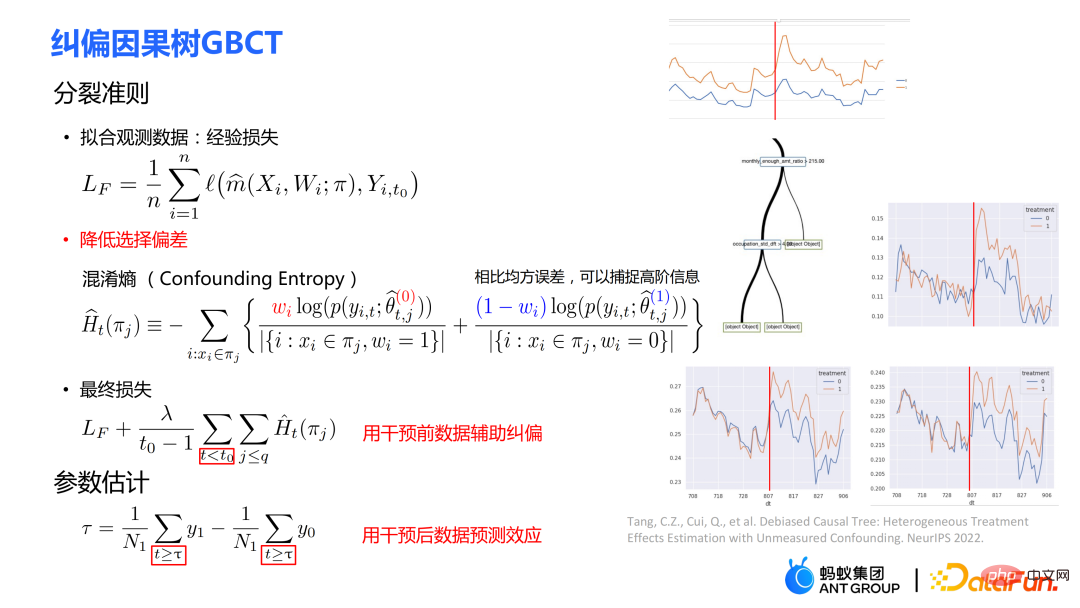 具体的なアプローチ:
具体的なアプローチ:
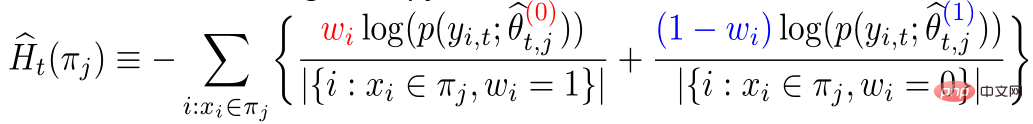
#② パラメータ推定
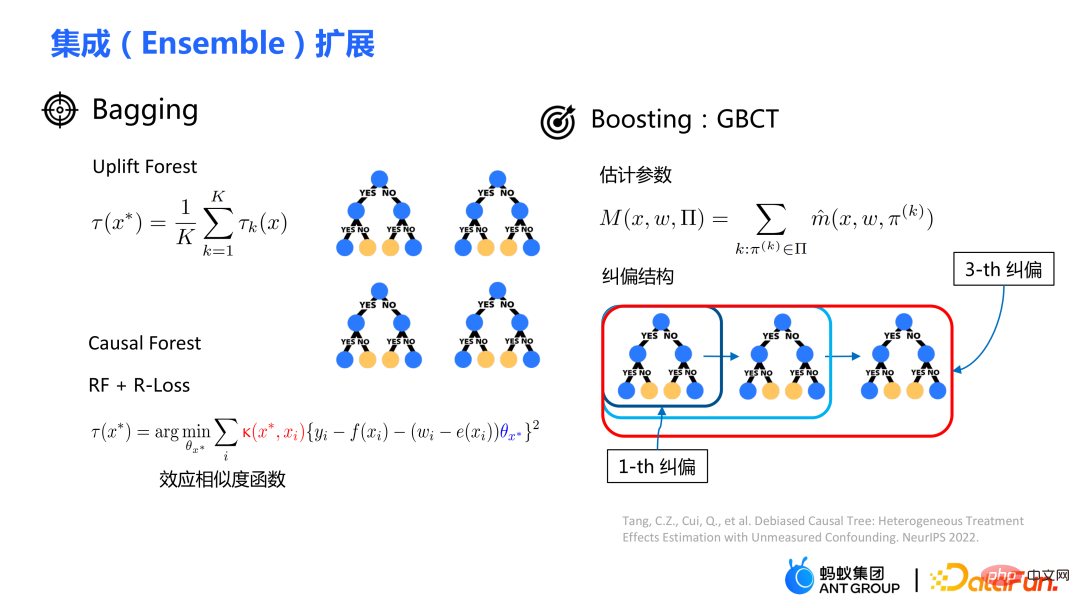

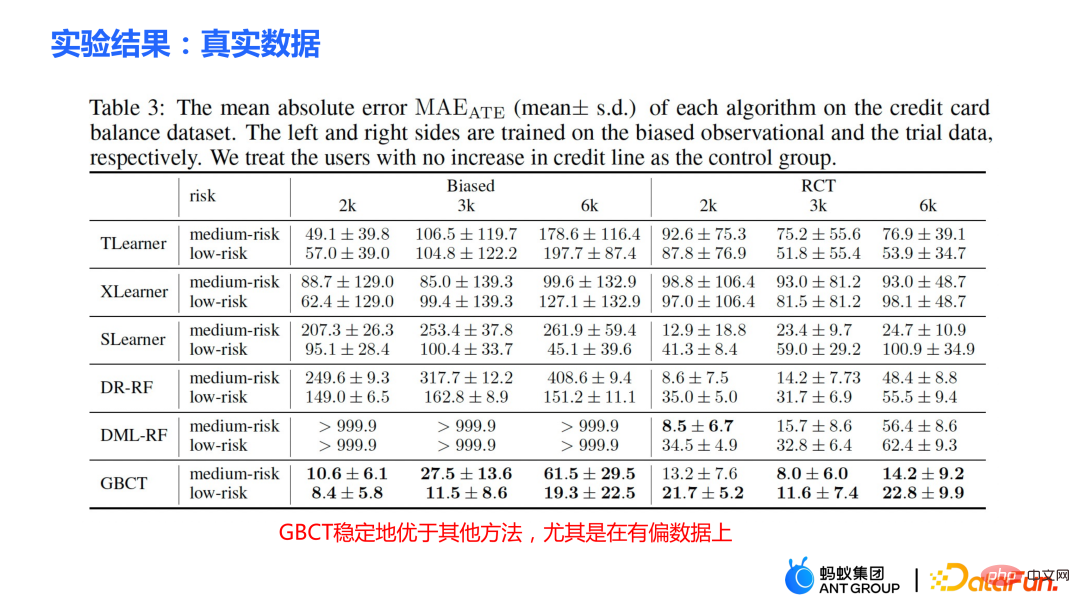 ②実際のクレジット カードの限度額引き上げデータ
②実際のクレジット カードの限度額引き上げデータ3. 因果データの融合

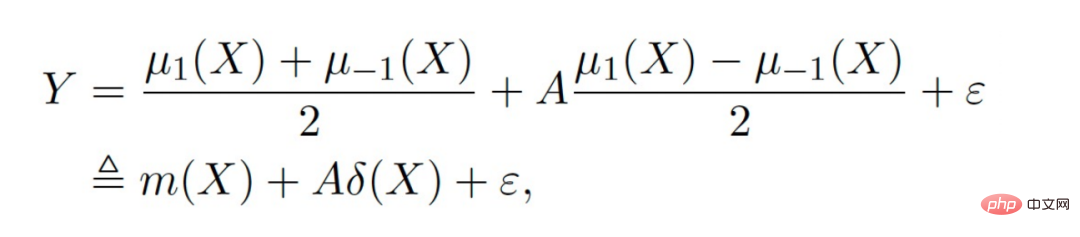
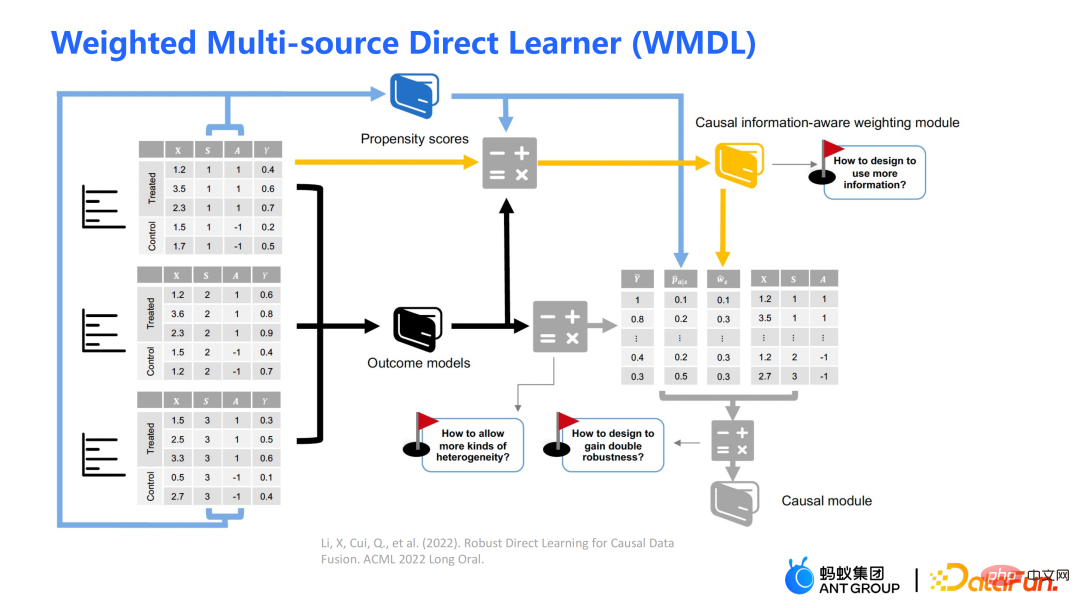 #WMDL アルゴリズムのフレームワーク図を上の図に示します。主なモジュールは次のとおりです:
#WMDL アルゴリズムのフレームワーク図を上の図に示します。主なモジュールは次のとおりです: #傾向スコア

 の分子は、後で説明する因果情報を認識した重み付けモジュールであり、これは私たちの研究の主な貢献です; 分母は、二重ロバスト手法の傾向スコアに似ていますが、この研究では両方のドメイン情報が含まれる点が異なります。が考慮されます。異なるドメイン間の因果関係が異なる場合には、そのドメインの指標情報も考慮されます。
の分子は、後で説明する因果情報を認識した重み付けモジュールであり、これは私たちの研究の主な貢献です; 分母は、二重ロバスト手法の傾向スコアに似ていますが、この研究では両方のドメイン情報が含まれる点が異なります。が考慮されます。異なるドメイン間の因果関係が異なる場合には、そのドメインの指標情報も考慮されます。 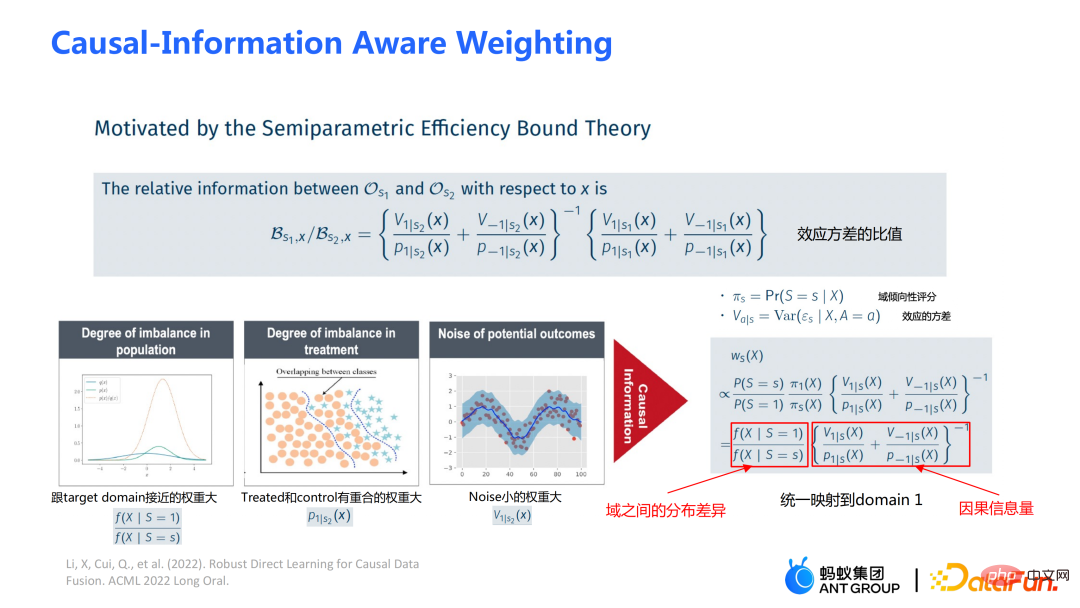
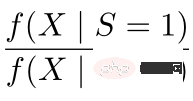 は、ドメイン間の分布の違いをバランスよく変換するためのモジュールです。
は、ドメイン間の分布の違いをバランスよく変換するためのモジュールです。 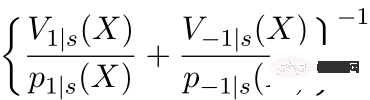 # は因果情報モジュールです。左側の 3 つの図は、ソース ドメインとターゲット ドメインの分布の差が大きい場合、ターゲット ドメインに近いサンプルが優先されます。
# は因果情報モジュールです。左側の 3 つの図は、ソース ドメインとターゲット ドメインの分布の差が大きい場合、ターゲット ドメインに近いサンプルが優先されます。 
#5. 質疑応答
#Q1: GBCT 補正と二重差分法 (した)?
Q2: GBCT は、観測されていない交絡変数に対してより優れたパフォーマンスを発揮します。より直観的な説明はありますか?
Q3: GBCT と Double Machine Learning (DML) を比較したことがありますか?
#Q4: ビジネスで遭遇する可能性のある同様の問題は、オフラインでの選択バイアスが存在する可能性があることです。ただし、オンラインのバイアスはオフラインのバイアスとは多少異なる場合があります。現時点では、オフラインで効果評価を行う場合、オフラインの効果をあまり正確に推定する方法がない可能性があります。
以上が因果推論でデータをより有効に活用するにはどうすればよいでしょうか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

