P/NP 問題は、計算複雑さの分野における未解決の問題です。人々は、「すべてのコンピューティングの問題を適切な時間内に効率的に解決できるか?」という質問に対する答えを見つけようと努めてきました。
適切な時間とは何ですか?実際、宇宙の終焉までに解決できる問題は、妥当な時間内に考慮されます。しかし、多くの問題は妥当な時間内に解決するのが難しいようであり、これらの問題の難しさを証明するには数学が必要です。
2021 年の調査では、上記の質問に対する答えが得られ、問題の大部分が効果的に解決するのが難しいことが確認されました。
ワシントン大学のポール・ビーム氏はこの研究について、「山に登るように、この研究は計算理論研究への道への足がかりとなる。」とコメントしました。
#この研究の 3 人の研究者: コンピューター科学者の Srikanth Srinivasan (左)、Nutan Limaye (右上)、Sébastien Tavenas。 
この研究では、加算と乗算のみを含む問題を検討しましたが、これらの問題は、特定の方法 (加算と乗算の特定の交互パターン) での解決に限定される場合、非常に困難になります。 驚くべきことに、この研究では新しいフレームワークやツールは使用されておらず、その代わりに、著者らは、高等研究所数学部の教授であるウィグダーソン氏とノーム氏との間の数十年にわたる共同研究を回避することに成功しました。エルサレムのヘブライ大学のニサン、作品の中で説明されている数学の壁。
研究者の一人、デンマークのオーフス大学のスリカンス・スリニバサン氏は、「この障害を回避する非常に簡単な方法があることに気づきました。そして、もしそのような簡単な方法でそれができるなら、何かが不可能だと思うなら、もっと良い方法を必ず見つけることができます。」
重要な質問
コンピューターの出現後、科学者たちはコンピューター アルゴリズムが多くの問題を解決できることを発見しましたが、これらのアルゴリズムにはコストがかかる場合があります。時間がかかりすぎます - 実際の計算時間より長くなります。
彼らは、問題の大きさに関係なく、一部の問題は本質的に解決が難しすぎるのではないかと疑い始めました。たとえば、グラフでは、ハミルトニアン パスが存在するかどうか、つまり各頂点を 1 回だけ通過するパスが存在するかどうかを判断することが重要な問題になります。頂点 (およびエッジ) の数を増やすと、そのようなパスが存在するかどうかを判断するのに時間がかかるはずですが、最良のアルゴリズムであっても、グラフ サイズが大きくなると指数関数的に時間がかかるため、この問題の解決は非現実的になります。
コンピュータ科学者は、特定の問題クラスの 1 つの困難な問題を解決するために何らかの方法で効果的なアルゴリズムは、同様に困難な他の問題の解決策に変換できることを証明しようとしています。彼らはこのタイプの問題を NP 問題と呼んでいます。 もちろん、難しくなさそうで、解決するのにそれほど時間がかからない問題もたくさんあります。これらの問題の多くはある意味で等価でもあり、このような問題は P 問題と呼ばれます。彼らは、NP 問題は実際には P 問題よりも難しく、NP 問題は決して効率的に解決できないと主張しています。しかし、証拠がなければ、この考えは間違っている可能性があります。
もちろん、難しくなさそうで、解決するのにそれほど時間がかからない問題もたくさんあります。これらの問題の多くはある意味で等価でもあり、このような問題は P 問題と呼ばれます。彼らは、NP 問題は実際には P 問題よりも難しく、NP 問題は決して効率的に解決できないと主張しています。しかし、証拠がなければ、この考えは間違っている可能性があります。
そこでコンピューター科学者たちは、NP 問題が実際に難しいことを証明する方法を探し始めました。そのためには、NP 問題を解くには指数関数的な時間がかかる必要があることを示す必要がありましたが、これを証明するのは簡単ではありませんでした。
「難しい」とはどれくらい難しいのでしょうか?
足し算と掛け算だけを必要とする特定の問題のセットを想像してください。たとえば、一連の点が与えられた場合、その点に関するデータを使用して、加算と乗算だけですべての可能なハミルトニアン パス (存在する場合) を計算することが可能です。
問題のサイズが大きくなると、一部の算術問題 (ハミルトニアン パスの計算など) に時間がかかります。 1979 年、ハーバード大学のレスリー ヴァリアントは、多くの算術問題は難易度の点で同等であるが、他の問題は難易度の点で同等であることを示しました。コンピューター科学者たちは後に、これら 2 種類の問題を、彼の名前にちなんで、それぞれ VNP と VP と名付けました。
P 問題や NP 問題と同様に、VNP 問題の難しさを証明することはできません。VNP 問題は NP 問題に基づいているため、NP 問題よりも難しいことだけがわかります。たとえば、パスがある場合は、まずパスを決定する必要があります。パスが存在するかどうか。
「NPよりも難しいので、難しいことを示すのは簡単なはずです」とシュピルカは言いました。
その後の数十年間で、コンピュータ科学者は、VP 対 VNP 問題に関して、P 対 NP 問題よりもはるかに大きな進歩を遂げましたが、そのほとんどは、Valiant の作成として知られる代数の複雑さのサブフィールドに限定されていました。 Limaye、Srinivasan、Tavenas による最近の研究が発表されるまでは、一般的な意味での算術に問題があるかどうかを判断することはまだ困難でした。
多項式の調整
この新しい研究は、コンピューター科学者が加算と乗算の問題についてどのように考えるかを探るのに役立ちます。数学的には、これらの問題は、加算および乗算される変数で構成される多項式 (例: x^2 5y 6) で記述することができます。
ハミルトニアン パスの計算など、特定の問題については、それを表す多項式を構築できます。たとえば、変数を使用して各点とエッジを表すことができ、より多くの点とエッジが追加されるにつれて、より多くの変数を多項式に追加できます。
ハミルトニアン パスの計算のような算術問題が難しいことを示すには、より多くの点とエッジが追加されると、対応する多項式を指数時間で解くためにより多くの演算が必要になることを示す必要があります。たとえば、x^2 には 1 つの演算 (x * x) が必要ですが、x^2 y には 2 つの演算 (x * x プラス y) が必要です。演算の数は多項式のサイズと呼ばれます。
しかし、多項式のサイズを決定するのは困難です。たとえば、多項式 x^2 2x 1 です。マグニチュード 4 (2 つの乗算と 2 つの加算) があるように見えますが、この多項式は 2 つの和の積 (x 1)(x 1) として書き換えることができ、オペランドが少なくなります (加算が 2 つ、乗算が 1 つ)。多くの場合、問題のサイズが大きくなり、より多くの変数が多項式に追加されると、数学的変換は問題のサイズを単純化し、縮小するのに役立ちます。
ヴァリアントの研究から数年後、コンピュータ科学者は問題の規模を分析しやすくする方法を発見しました。これを行うために、彼らは、多項式が切り替わる回数、または和と積の間で切り替わる回数を指定する「深さ」と呼ばれるプロパティを提案しました。たとえば、多項式 x^2 2x 1 は積の和 (x^2 と 2x など) であるため、深さは 2 になります。対照的に、式 (x 1)(x 1) は、積の和として 0 (x 1)(x 1) と同じ深さを持つため、深さは 3 になります。

多項式を簡素化するために、コンピューター科学者は多項式を「一定の深さ」と呼ばれる特性を備えた固定形式に制約します。この場合、和と積のパターンは時間の経過とともに変化しません。問題が大きくなるにつれて変化します。これにより、多項式のサイズがより固定され、深さが増加するにつれて多項式のサイズが減少します。一定の深さの式は式と呼ばれます。深さが一定であるため、多項式の研究をさらに進めることができます。
魔法の「深さ」
1996 年、ニサンとウィグダーソンによる論文は行列の乗算の問題の解決に焦点を当て、この問題を 2 つの方法で単純化しました。まず、深さ一定、つまり深さ 3 の公式を使用してそれを表現しました。第 2 に、彼らは各変数の最大指数が 1 である単純な構造を持つ式のみを考慮しており、元の問題は「多重線形」問題になります。
コンピュータ科学者は、多項式のサイズが(指数関数的増加の増加率に匹敵する)準指数関数的に増加することを犠牲にして、特定の問題を比較的単純な集合多重線形構造に変換できることを発見しました。
Nisan と Wigderson はその後、行列の乗算問題は行列が大きくなるにつれて解くのに指数関数的な時間がかかることを示しました。言い換えれば、彼らは重要な問題が難しいことを示し、あるクラスの問題が難しいことを示すために努力します。ただし、その結果は、単純な集合的な多重線形構造を持つ定式化にのみ当てはまります。

Leslie Valiant
多項式の深さを増やすと、多くの場合、そのサイズが減少します。コンピュータ科学者は、時間の経過とともに、これら 2 つの特性間のトレードオフをより正確にしてきました。彼らは、深さ 3 に 2 つの深さレベルを追加すると、アンサンブル多重線形多項式がアンサンブル多重線形構造のサイズ ゲインのバランスを取ることができることを示しています。深さ 5 の構造化された数式に指数関数的な時間がかかる場合、一般的な構造化されていない性質の深さ 3 の数式も同様です。
Srikanth Srinivasan らによる新しい研究は、行列乗算問題の深い 5 集合の多線形定式化が実際に指数関数的な速度で増大することを示しています。これは、一般的な深さ 3 の式にも指数関数的な時間がかかることを意味します。次に、同様のパターンがすべての深さ (3 と 5 だけでなく) に当てはまることを示しました。この関係により、彼らは、同じ問題に対する一般的な式のサイズは、問題のサイズに応じて指数関数的に増大することを示しました。
また、深さがどのようなものであっても、深さが一定の式で行列の乗算を表現するのは難しいことも示しています。
この研究の結果は、算術問題が「難しい」場合、つまり深さが一定の式で表現できない場合について、初めて一般的な理解を提供します。行列乗算の特定の問題は、VP 問題として知られています。そして、VP 問題は一定の深さに制限されない場合には比較的簡単であることが知られており、一定の深さが問題の「難しさ」の原因であることがわかります。
VNP の問題は VP の問題よりも難しいですか?新しい結果はこれを直接示しているわけではなく、一定の深さの公式が難しいことを示しているだけです。しかし、これは依然として、VNP 問題が VP 問題と同等ではないことを証明する重要なマイルストーンです。
より大きな P 対 NP の問題については、いつか答えが見つかるだろうとより楽観的になれるようになりました。結局のところ、難しい問題を解決するには、まずどの方向が絶望的であるかを知る必要があります。
以上が問題が VPN の問題であることを証明するにはどうすればよいですか?コンピューター科学者は簡単な方法を見つけましたの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 踊りましょう:私たちの人間のニューラルネットを微調整するための構造化された動きApr 27, 2025 am 11:09 AM
踊りましょう:私たちの人間のニューラルネットを微調整するための構造化された動きApr 27, 2025 am 11:09 AM科学者は、彼らの機能を理解するために、人間とより単純なニューラルネットワーク(C. elegansのものと同様)を広く研究してきました。 ただし、重要な疑問が生じます。新しいAIと一緒に効果的に作業するために独自のニューラルネットワークをどのように適応させるのか
 新しいGoogleリークは、Gemini AIのサブスクリプションの変更を明らかにしますApr 27, 2025 am 11:08 AM
新しいGoogleリークは、Gemini AIのサブスクリプションの変更を明らかにしますApr 27, 2025 am 11:08 AMGoogleのGemini Advanced:Horizonの新しいサブスクリプションティア 現在、Gemini Advancedにアクセスするには、1か月あたり19.99ドルのGoogle One AIプレミアムプランが必要です。 ただし、Android Authorityのレポートは、今後の変更を示唆しています。 最新のGoogle p
 データ分析の加速がAIの隠されたボトルネックをどのように解決しているかApr 27, 2025 am 11:07 AM
データ分析の加速がAIの隠されたボトルネックをどのように解決しているかApr 27, 2025 am 11:07 AM高度なAI機能を取り巻く誇大宣伝にもかかわらず、エンタープライズAIの展開内に大きな課題が潜んでいます:データ処理ボトルネック。 CEOがAIの進歩を祝う間、エンジニアはクエリの遅い時間、過負荷のパイプライン、
 MarkitDown MCPは、任意のドキュメントをマークダウンに変換できます!Apr 27, 2025 am 09:47 AM
MarkitDown MCPは、任意のドキュメントをマークダウンに変換できます!Apr 27, 2025 am 09:47 AMドキュメントの取り扱いは、AIプロジェクトでファイルを開くだけでなく、カオスを明確に変えることです。 PDF、PowerPoint、Wordなどのドキュメントは、あらゆる形状とサイズでワークフローをフラッシュします。構造化された取得
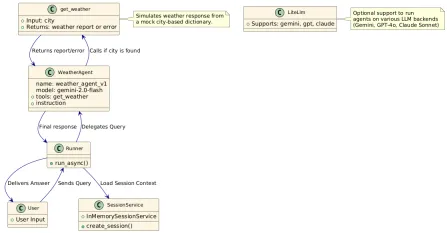 建物のエージェントにGoogle ADKを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:42 AM
建物のエージェントにGoogle ADKを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:42 AMGoogleのエージェント開発キット(ADK)のパワーを活用して、実際の機能を備えたインテリジェントエージェントを作成します。このチュートリアルは、ADKを使用して会話エージェントを構築し、GeminiやGPTなどのさまざまな言語モデルをサポートすることをガイドします。 w
 効果的な問題解決のためにLLMを介したSLMの使用 - 分析VidhyaApr 27, 2025 am 09:27 AM
効果的な問題解決のためにLLMを介したSLMの使用 - 分析VidhyaApr 27, 2025 am 09:27 AMまとめ: Small Language Model(SLM)は、効率のために設計されています。それらは、リソース不足、リアルタイム、プライバシーに敏感な環境の大手言語モデル(LLM)よりも優れています。 特にドメインの特異性、制御可能性、解釈可能性が一般的な知識や創造性よりも重要である場合、フォーカスベースのタスクに最適です。 SLMはLLMSの代替品ではありませんが、精度、速度、費用対効果が重要な場合に理想的です。 テクノロジーは、より少ないリソースでより多くを達成するのに役立ちます。それは常にドライバーではなく、プロモーターでした。蒸気エンジンの時代からインターネットバブル時代まで、テクノロジーの力は、問題の解決に役立つ範囲にあります。人工知能(AI)および最近では生成AIも例外ではありません
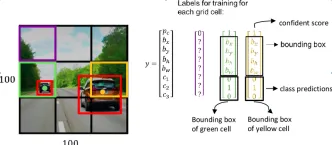 コンピュータービジョンタスクにGoogle Geminiモデルを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:26 AM
コンピュータービジョンタスクにGoogle Geminiモデルを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:26 AMコンピュータービジョンのためのGoogleGeminiの力を活用:包括的なガイド 大手AIチャットボットであるGoogle Geminiは、その機能を会話を超えて拡張して、強力なコンピュータービジョン機能を網羅しています。 このガイドの利用方法については、
 Gemini 2.0 Flash vs O4-Mini:GoogleはOpenaiよりもうまくやることができますか?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs O4-Mini:GoogleはOpenaiよりもうまくやることができますか?Apr 27, 2025 am 09:20 AM2025年のAIランドスケープは、GoogleのGemini 2.0 FlashとOpenaiのO4-Miniの到着とともに感動的です。 数週間離れたこれらの最先端のモデルは、同等の高度な機能と印象的なベンチマークスコアを誇っています。この詳細な比較


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

Safe Exam Browser
Safe Exam Browser は、オンライン試験を安全に受験するための安全なブラウザ環境です。このソフトウェアは、あらゆるコンピュータを安全なワークステーションに変えます。あらゆるユーティリティへのアクセスを制御し、学生が無許可のリソースを使用するのを防ぎます。

VSCode Windows 64 ビットのダウンロード
Microsoft によって発売された無料で強力な IDE エディター

WebStorm Mac版
便利なJavaScript開発ツール

PhpStorm Mac バージョン
最新(2018.2.1)のプロフェッショナル向けPHP統合開発ツール

ホットトピック
 7759
7759 15
15 1644
1644 14
14 1399
1399 52
52 1293
1293 25
25 1234
1234 29
29



