ホームページ >テクノロジー周辺機器 >AI >Tongji と Alibaba の CVPR 2022 Best Student Paper Awards では何を研究しましたか?これはある作品の解釈です
Tongji と Alibaba の CVPR 2022 Best Student Paper Awards では何を研究しましたか?これはある作品の解釈です
- PHPz転載
- 2023-04-09 13:41:091547ブラウズ
この記事では、CVPR 2022 Best Student Paper Awardを受賞した私たちの研究「EPro-PnP: Generalized End-to-End Probabilistic Perspective-n-Points for Monocular Object Pose Estimation」について説明します。この論文で研究する問題は、単一の画像に基づいて 3D 空間内のオブジェクトの姿勢を推定することです。既存の手法のうち、PnP 幾何最適化に基づく姿勢推定手法は、ディープネットワークを通じて 2D-3D 関連点を抽出することが多いですが、バックプロパゲーションでは姿勢の最適解が微分できないため、損失が安定して動作するため姿勢誤差を利用することが困難です。 2D-3D 相関ポイントが他のエージェント損失の監視に依存している場合、ネットワークのエンドツーエンド トレーニング。これは姿勢推定の最適なトレーニング目標ではありません。
この問題を解決するために、私たちは理論に基づいて、姿勢の単一の最適解の代わりに姿勢の確率密度分布を出力する EPro-PnP モジュールを提案しました。したがって、微分不可能な最適姿勢が微分可能な確率密度に置き換えられ、安定したエンドツーエンドのトレーニングが実現します。 EPro-PnP は汎用性が高く、さまざまな特定のタスクやデータに適しています。既存の PnP ベースの姿勢推定方法を改善するために使用したり、その柔軟性を利用して新しいネットワークをトレーニングしたりすることもできます。より一般的な意味では、EPro-PnP は基本的に共通分類ソフトマックスを連続領域に導入し、理論的には入れ子になった最適化層を使用して一般モデルをトレーニングするように拡張できます。

紙のリンク: https://arxiv.org/abs/2203.13254
コードリンク: https://github.com/tjiiv-cprg/EPro-PnP
1.序文 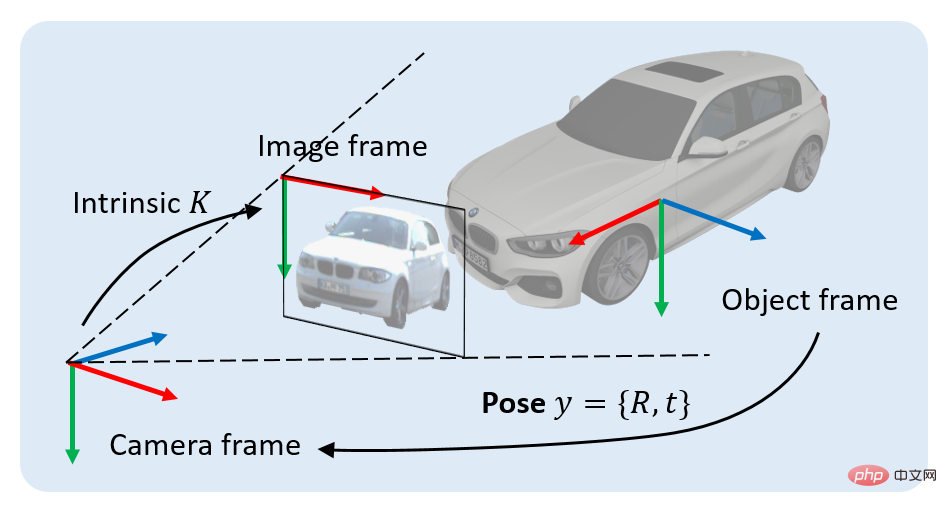
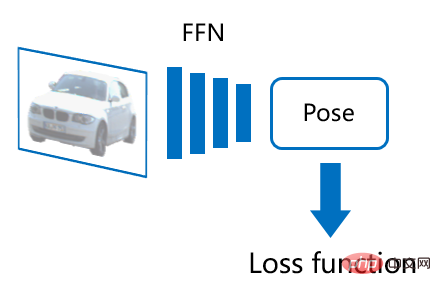 #この問題に対処するために、既存のメソッドは明示的メソッドと暗黙的メソッドの 2 つのカテゴリに分類できます。この明示的な方法は、
#この問題に対処するために、既存のメソッドは明示的メソッドと暗黙的メソッドの 2 つのカテゴリに分類できます。この明示的な方法は、
直接姿勢予測と呼ばれることもあり、フィードフォワード ニューラル ネットワーク (FFN) を使用してオブジェクトの姿勢の各コンポーネントを直接出力します。通常は次のとおりです。 1) オブジェクトの姿勢を予測します。深さ、2) 画像上の物体の中心点の 2D 投影位置を見つけます、3) 物体の向きを予測します (向きの具体的な処理方法はより複雑になる可能性があります)。オブジェクトの真の姿勢でマークされた画像データを使用すると、姿勢予測結果を直接監視する損失関数を設計でき、ネットワークのエンドツーエンドのトレーニングを簡単に実現できます。ただし、このようなネットワークは解釈可能性に欠けており、小さなデータセットでは過剰適合する傾向があります。 3D オブジェクト検出タスクでは、特に大規模なデータセット (nuScenes など) の場合、明示的手法が主流です。
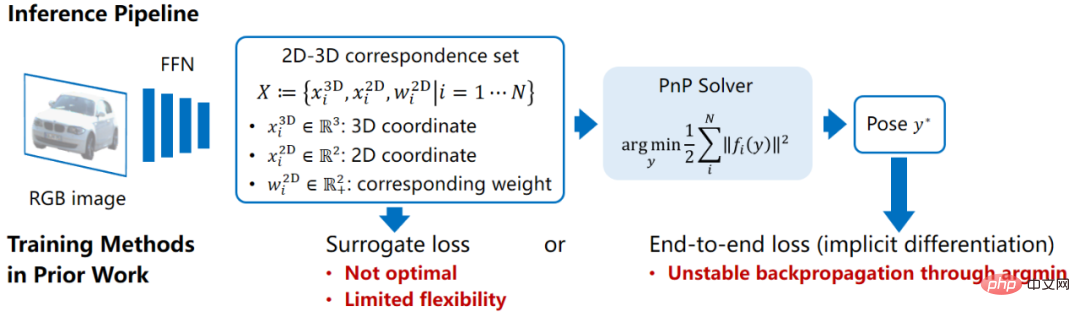
陰的解法は幾何最適化に基づく姿勢推定手法であり、最も代表的なのはPnPに基づく姿勢推定手法です。このタイプの方法では、まず画像座標系で N 個の 2D 点を見つける必要があります (i 番目の点の 2D 座標は  とマークされています)。同時に、関連するオブジェクト座標系の点。N 個の 3D 点 (i 番目の点の 3D 座標は
とマークされています)。同時に、関連するオブジェクト座標系の点。N 個の 3D 点 (i 番目の点の 3D 座標は  としてマークされます)、場合によっては、点の各ペアに関連する重みを取得する必要があります ( i 番目の点のペアに関連付けられた重みは、
としてマークされます)、場合によっては、点の各ペアに関連する重みを取得する必要があります ( i 番目の点のペアに関連付けられた重みは、 としてマークされます。透視投影制約に従って、これらの N 対の 2D-3D 重み付け関連点は、オブジェクトの最適な姿勢を暗黙的に定義します。具体的には、再投影誤差を最小限に抑えるオブジェクトのポーズを見つけることができます。
としてマークされます。透視投影制約に従って、これらの N 対の 2D-3D 重み付け関連点は、オブジェクトの最適な姿勢を暗黙的に定義します。具体的には、再投影誤差を最小限に抑えるオブジェクトのポーズを見つけることができます。  #:
#:
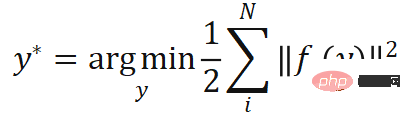
where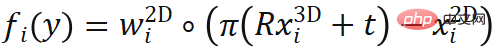 は、ポーズの関数
は、ポーズの関数  である重み付き再投影誤差を表します。
である重み付き再投影誤差を表します。  は内部パラメータを含むカメラ投影関数を表し、
は内部パラメータを含むカメラ投影関数を表し、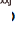 は要素積を表します。 PnP 手法は、オブジェクトのジオメトリが既知である 6 自由度の姿勢推定タスクで一般的に使用されます。。
は要素積を表します。 PnP 手法は、オブジェクトのジオメトリが既知である 6 自由度の姿勢推定タスクで一般的に使用されます。。
## #。直接的な姿勢予測と比較して、従来の幾何学視覚アルゴリズムと組み合わせたこの深層学習モデルは非常に優れた解釈性を持ち、一般化パフォーマンスは比較的安定していますが、以前の研究のモデルトレーニング方法には欠陥がありました。多くの方法では、中間結果 X を監視する代理損失関数を構築しますが、これはポーズの最適な目標ではありません。たとえば、オブジェクトの形状がわかっている場合は、オブジェクトの 3D キー ポイントを事前に選択し、対応する 2D 投影点の位置を見つけるようにネットワークをトレーニングします。これは、サロゲート損失が X の変数の一部しか学習できないため、十分な柔軟性がないことも意味します。トレーニング セット内のオブジェクトの形状が分からず、X のすべてを最初から学習する必要がある場合はどうすればよいでしょうか? 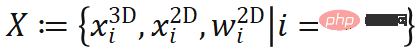 陽的解法と陰的解法には相補的な利点があります。PnP によって出力されたポーズ結果を監視することによって、ネットワークをエンドツーエンドで学習して、関連する点セット X を学習できる場合、この 2 つは、組み合わせることができます。 利点を組み合わせることができます。この目標を達成するために、最近の研究では、暗黙的な関数導出を使用して PnP 層のバックプロパゲーションを実装しました。ただし、PnP の argmin 関数は特定の点で不連続で微分不可能であるため、バックプロパゲーションが不安定になり、直接トレーニングの収束が困難になります。
陽的解法と陰的解法には相補的な利点があります。PnP によって出力されたポーズ結果を監視することによって、ネットワークをエンドツーエンドで学習して、関連する点セット X を学習できる場合、この 2 つは、組み合わせることができます。 利点を組み合わせることができます。この目標を達成するために、最近の研究では、暗黙的な関数導出を使用して PnP 層のバックプロパゲーションを実装しました。ただし、PnP の argmin 関数は特定の点で不連続で微分不可能であるため、バックプロパゲーションが不安定になり、直接トレーニングの収束が困難になります。
2. EPro-PnP メソッドの紹介
1. EPro-PnP モジュール

安定した終了を達成するために-to-end トレーニングには、 エンドツーエンドの確率的 PnP (エンドツーエンドの確率的 PnP)、つまり EPro-PnP を提案します。基本的な考え方は、暗黙のポーズを確率分布とみなすことです。その場合、その確率密度  は X について微分可能です。まず、再投影誤差に基づいてポーズの尤度関数を定義します。
は X について微分可能です。まず、再投影誤差に基づいてポーズの尤度関数を定義します。
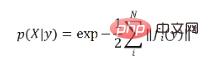

有益でない事前分布が使用される場合、確率密度は、尤度関数の正規化された結果です。
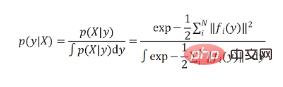

上記の式は次の式と一致していることに注意してください。一般的に使用される分類ソフトマックス式 ポイントは近いです。実際、EPro-PnP の本質は、ソフトマックスを離散しきい値から連続しきい値に移動し、合計を置き換えることです
ポイントは近いです。実際、EPro-PnP の本質は、ソフトマックスを離散しきい値から連続しきい値に移動し、合計を置き換えることです  整数
整数 。
。
2. KL 発散損失
モデルのトレーニングの過程で、オブジェクトの真の姿勢がわかっている場合、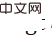 ターゲットポーズ分布
ターゲットポーズ分布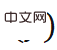 #を定義できます。このとき、KL ダイバージェンス
#を定義できます。このとき、KL ダイバージェンス 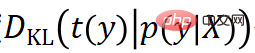 は、ネットワークの学習に使用される損失関数として計算できます (
は、ネットワークの学習に使用される損失関数として計算できます (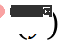 は固定なので、クロスとしても理解できます) -エントロピー損失関数)。ターゲット
は固定なので、クロスとしても理解できます) -エントロピー損失関数)。ターゲット  # がディラック関数に近づくと、KL 発散に基づく損失関数は次の形式に簡略化できます。
# がディラック関数に近づくと、KL 発散に基づく損失関数は次の形式に簡略化できます。
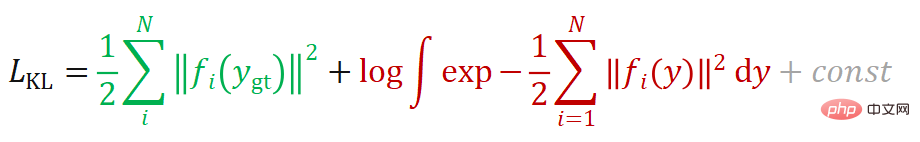
## その導関数を導出したい場合:
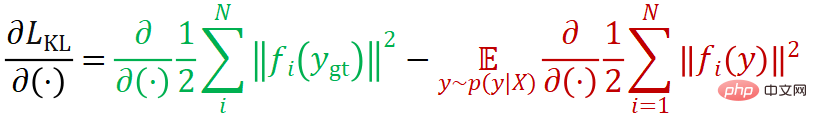
損失関数は 2 つの項目で構成されていることがわかります。最初の項目 ( と表示) は、ポーズの真の値の再投影を低減しようとします
と表示) は、ポーズの真の値の再投影を低減しようとします  エラー。2 番目の項 (
エラー。2 番目の項 ( として示される) は、予測されたポーズ
として示される) は、予測されたポーズ  のあらゆる場所で再投影誤差を増加させようとします。 2 つの方向は逆であり、その効果は次の図 (左) に示されています。類似として、右側は、分類ネットワークをトレーニングするときに一般的に使用されるカテゴリカルクロスエントロピー損失です。
のあらゆる場所で再投影誤差を増加させようとします。 2 つの方向は逆であり、その効果は次の図 (左) に示されています。類似として、右側は、分類ネットワークをトレーニングするときに一般的に使用されるカテゴリカルクロスエントロピー損失です。
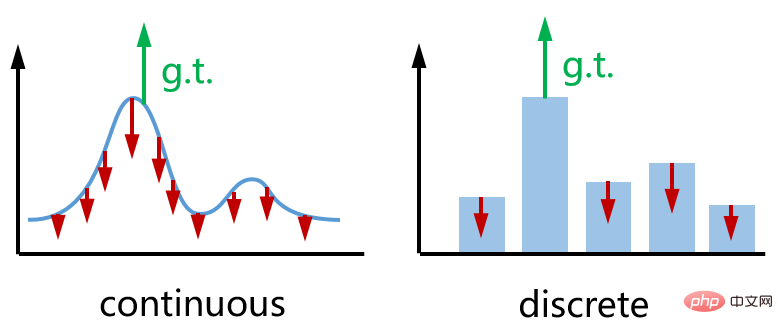
KL 損失の 2 番目の項に注意してください# には積分が含まれています。この積分には解析的な解がないため、数値的手法で近似する必要があります。汎用性、精度、計算効率を考慮して、モンテカルロ法を使用してサンプリングを通じて姿勢分布をシミュレートします。 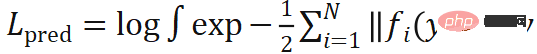

重み  を付けて、このプロセスをモンテカルロ PnP と呼びます。
を付けて、このプロセスをモンテカルロ PnP と呼びます。 
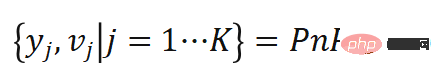
# は重みに関する関数  として近似でき、
として近似でき、 は逆伝播できます。
は逆伝播できます。 
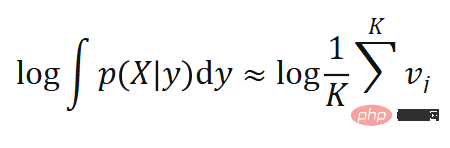
4. PnP ソルバーの微分正則化
モンテカルロ PnP 損失を使用してネットワークをトレーニングして高品質の姿勢分布を取得することはできますが、推論段階では依然として PnP が必要です。最適なポーズの解決策を取得するためのソルバー #。一般的に使用されるガウス ニュートン アルゴリズムとその導関数は、反復最適化を通じて
#。一般的に使用されるガウス ニュートン アルゴリズムとその導関数は、反復最適化を通じて  を解き、その反復増分はコスト関数 の 1 次導関数と 2 次導関数によって決定されます。
を解き、その反復増分はコスト関数 の 1 次導関数と 2 次導関数によって決定されます。  。 PnP
。 PnP  の解を真の値
の解を真の値  に近づけるために、コスト関数の導関数を正規化できます。正則化損失関数は次のように設計されています。
に近づけるために、コスト関数の導関数を正規化できます。正則化損失関数は次のように設計されています。
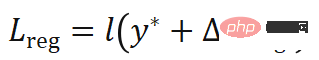
このうち、 はガウス-ニュートン反復増分であり、およびコスト関数 1 次導関数と 2 次導関数は関連しており、逆伝播することができます。
はガウス-ニュートン反復増分であり、およびコスト関数 1 次導関数と 2 次導関数は関連しており、逆伝播することができます。 は距離メトリックを表し、位置には滑らかな L1 を、方向にはコサイン類似度を使用します。
は距離メトリックを表し、位置には滑らかな L1 を、方向にはコサイン類似度を使用します。  が矛盾している場合、この損失関数により、反復増分
が矛盾している場合、この損失関数により、反復増分  が実際の真の値を指すようになります。
が実際の真の値を指すようになります。
に基づく姿勢推定ネットワーク 6 自由度の姿勢推定と 3D ターゲット検出ネットワークにさまざまなサブタスクを使用します。このうち、6 自由度の姿勢推定については、ICCV 2019 の CDPN ネットワークに基づいてわずかに修正され、アブレーション研究を実施するために EPro-PnP でトレーニングされ、3D ターゲット検出については、それに基づいてまったく新しいネットワークが設計されています。 ICCVW 2021 の FCOS3D で。変形可能な対応検出ヘッドは、EPro-PnP がオブジェクト形状の知識がなくても、すべての 2D-3D 点と関連重みを直接学習するようにネットワークをトレーニングできることを証明し、アプリケーションにおける EPro-PnP の柔軟性を実証します。
1. 6-DOF 姿勢推定のための高密度相関ネットワーク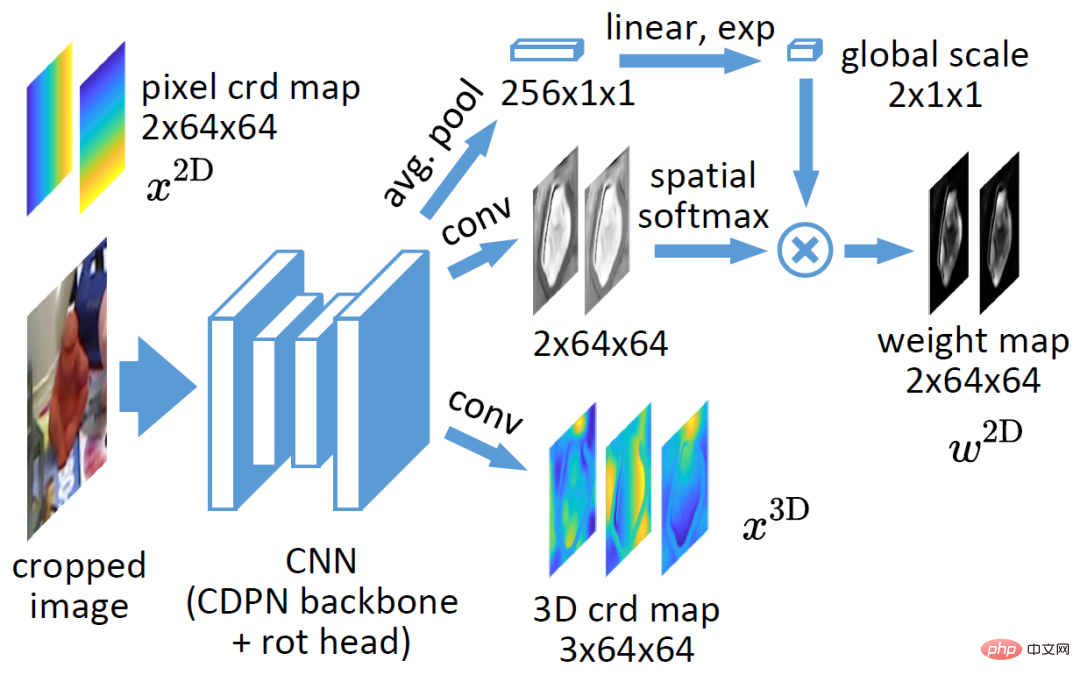
ネットワーク構造は上の図に示されていますが、出力層が元の CDPN に基づいて変更されている点が異なります。元の CDPN は、検出されたオブジェクト 2D ボックスを使用して領域画像を切り出し、それを ResNet34 バックボーンに入力します。オリジナルの CDPN は、位置と方向を 2 つの分岐に分離しており、位置分岐では直接予測の陽的手法が使用され、方向分岐では密な関連付けと PnP の陰的手法が使用されます。 EPro-PnP を研究するために、変更されたネットワークは密な相関ブランチのみを保持します。その出力は 3 チャネル 3D 座標マップと 2 チャネルの相関重みであり、相関重みには空間ソフトマックスとグローバル ウェイト スケーリングが適用されます。空間ソフトマックスを追加する目的は、重み  を正規化して、アテンション マップと同様の特性を持ち、比較的重要な領域に焦点を当てることができるようにすることです。実験では、重みの正規化が安定した収束の鍵でもあることが証明されました。 。グローバル ウェイト スケーリングは、ポーズ分布の集中度を反映します。ネットワークは、オブジェクトの形状が既知である場合、微分正則化と追加の 3D 座標回帰損失を追加することに加えて、EPro-PnP のモンテカルロ姿勢損失のみを使用してトレーニングできます。
を正規化して、アテンション マップと同様の特性を持ち、比較的重要な領域に焦点を当てることができるようにすることです。実験では、重みの正規化が安定した収束の鍵でもあることが証明されました。 。グローバル ウェイト スケーリングは、ポーズ分布の集中度を反映します。ネットワークは、オブジェクトの形状が既知である場合、微分正則化と追加の 3D 座標回帰損失を追加することに加えて、EPro-PnP のモンテカルロ姿勢損失のみを使用してトレーニングできます。  2. 3D ターゲット検出のための変形相関ネットワーク
2. 3D ターゲット検出のための変形相関ネットワーク
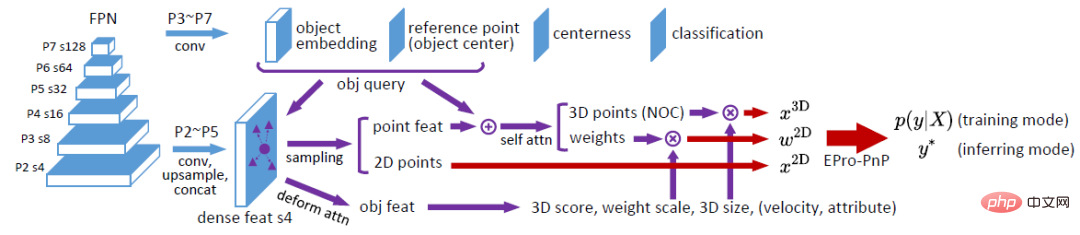 ネットワーク構造は上図に示されています。一般に、FCOS3D 検出器に基づいており、変形可能な DETR によって設計されたネットワーク構造を指します。 FCOS3D に基づいて、その中心性層と分類層は保持され、元の姿勢予測層はオブジェクト クエリを生成するためのオブジェクト埋め込み層と参照点層に置き換えられます。変形可能な DETR を参照すると、参照点に対する相対的なオフセットを予測することによって 2D サンプリング位置が取得されます (したがって、
ネットワーク構造は上図に示されています。一般に、FCOS3D 検出器に基づいており、変形可能な DETR によって設計されたネットワーク構造を指します。 FCOS3D に基づいて、その中心性層と分類層は保持され、元の姿勢予測層はオブジェクト クエリを生成するためのオブジェクト埋め込み層と参照点層に置き換えられます。変形可能な DETR を参照すると、参照点に対する相対的なオフセットを予測することによって 2D サンプリング位置が取得されます (したがって、
が得られます)。サンプリングされた特徴は、アテンション操作を通じてオブジェクト フィーチャに集約され、オブジェクト レベルの結果 (3D スコア、重量スケール、3D ボックス サイズなど) を予測するために使用されます。さらに、サンプリング後、各点の特徴がオブジェクト埋め込みで追加され、自己注意によって処理されて、それぞれに対応する 3D 座標  と関連する重み
と関連する重み  が出力されます。ポイント。予測されたすべての
が出力されます。ポイント。予測されたすべての  # は、EPro-PnP のモンテカルロ ポーズ損失トレーニングによって取得でき、追加の正則化なしで収束して高精度を達成できます。これに基づいて、微分正則化損失と補助損失を追加して精度をさらに向上させることができます。
# は、EPro-PnP のモンテカルロ ポーズ損失トレーニングによって取得でき、追加の正則化なしで収束して高精度を達成できます。これに基づいて、微分正則化損失と補助損失を追加して精度をさらに向上させることができます。  4. 実験結果
4. 実験結果
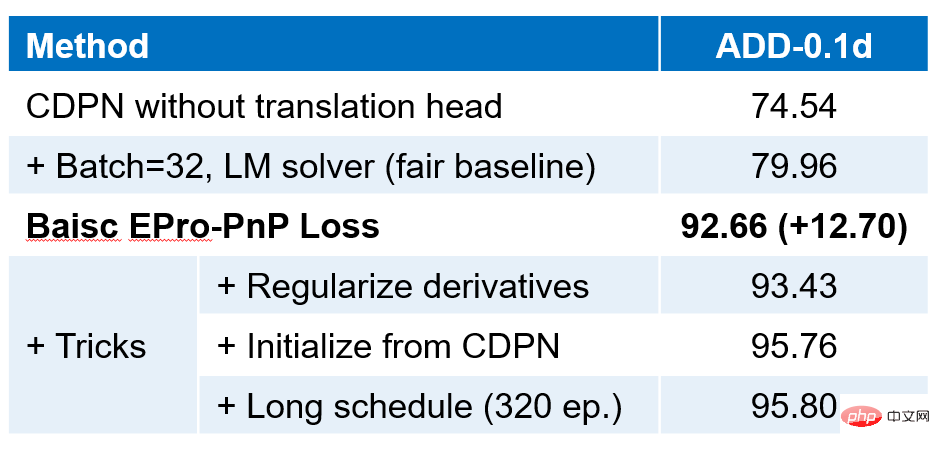 使用LineMOD データセットの実験と CDPN ベースラインとの厳密な比較、主な結果は上記のとおりです。エンドツーエンドのトレーニングに EPro-PnP 損失を追加すると、精度が大幅に向上することがわかります (12.70)。微分正則化損失を増加し続けると、精度がさらに向上します。これに基づいて、元の CDPN のトレーニング結果を使用してエポックを初期化および増加する (エポックの総数を元の CDPN の完全な 3 段階のトレーニングと一致させる) と、精度をさらに向上させることができます。トレーニング CDPN は、CDPN の追加トレーニング、マスク監視から来ています。
使用LineMOD データセットの実験と CDPN ベースラインとの厳密な比較、主な結果は上記のとおりです。エンドツーエンドのトレーニングに EPro-PnP 損失を追加すると、精度が大幅に向上することがわかります (12.70)。微分正則化損失を増加し続けると、精度がさらに向上します。これに基づいて、元の CDPN のトレーニング結果を使用してエポックを初期化および増加する (エポックの総数を元の CDPN の完全な 3 段階のトレーニングと一致させる) と、精度をさらに向上させることができます。トレーニング CDPN は、CDPN の追加トレーニング、マスク監視から来ています。
上の図は、EPro-PnP とさまざまな主要な手法との比較です。バックワード CDPN から改良された EPro-PnP は、精度が SOTA に近く、EPro-PnP のアーキテクチャはシンプルです。姿勢推定は完全に PnP に基づいており、追加の明示的な深度推定やポーズの調整は必要ありません。したがって、効率の面でもメリットがあります。
2. 3D ターゲット検出タスク
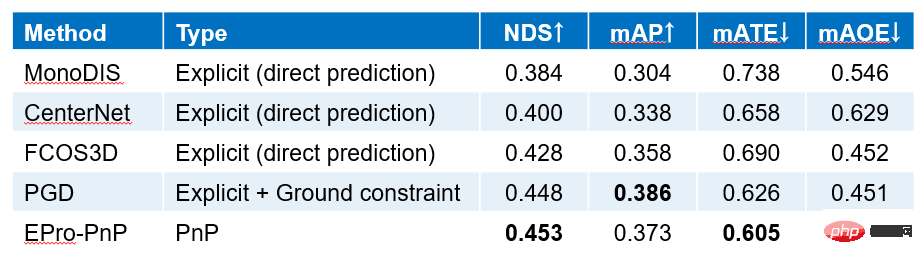
nuScenes データセット実験を使用した、他の方法と比較した結果を次の表に示します。上の図。 EPro-PnP は FCOS3D よりも大幅に改善されているだけでなく、当時の SOTA および FCOS3D のもう 1 つの改良バージョンである PGD も上回っています。さらに重要なことは、EPro-PnP は現在、nuScenes データセット上の姿勢を推定するために幾何学的最適化手法を使用する唯一のものです。 nuScenes データセットが大規模であるため、エンドツーエンドでトレーニングされた直接姿勢推定ネットワークはすでに良好なパフォーマンスを示しており、私たちの結果は、幾何最適化に基づくモデルのエンドツーエンド トレーニングがより優れたパフォーマンスを達成できることを示しています。大規模なデータセット、優れたパフォーマンス。
3. 視覚分析
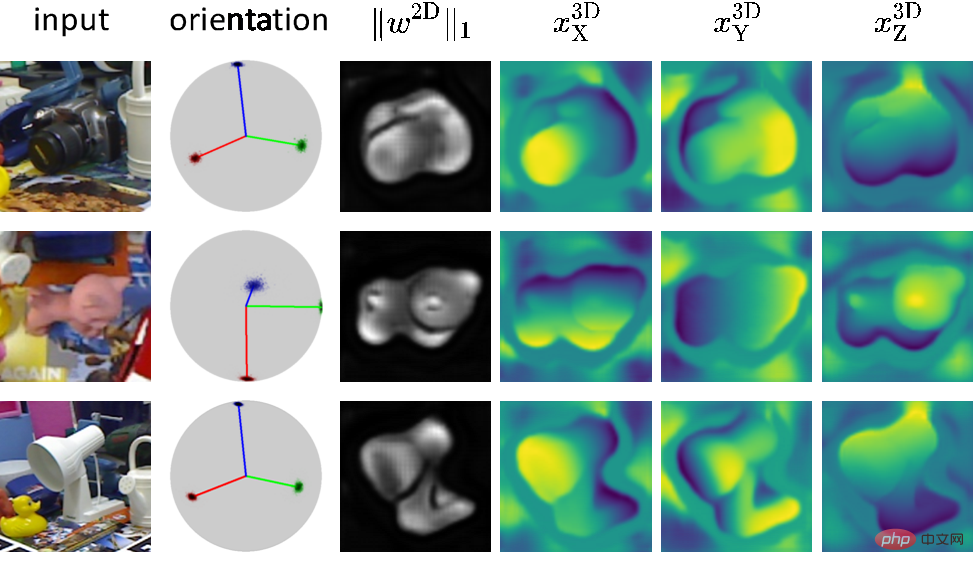
上の図は、EPro-PnP でトレーニングされた密結合ネットワークの予測結果を示しています。その中で、相関重みgraph は、注意メカニズムと同様に、画像内の重要な領域を強調表示します。損失関数分析から、ハイライト領域は再投影の不確実性が低い領域に対応しており、姿勢の変化に対してより敏感であることがわかります。
は、注意メカニズムと同様に、画像内の重要な領域を強調表示します。損失関数分析から、ハイライト領域は再投影の不確実性が低い領域に対応しており、姿勢の変化に対してより敏感であることがわかります。
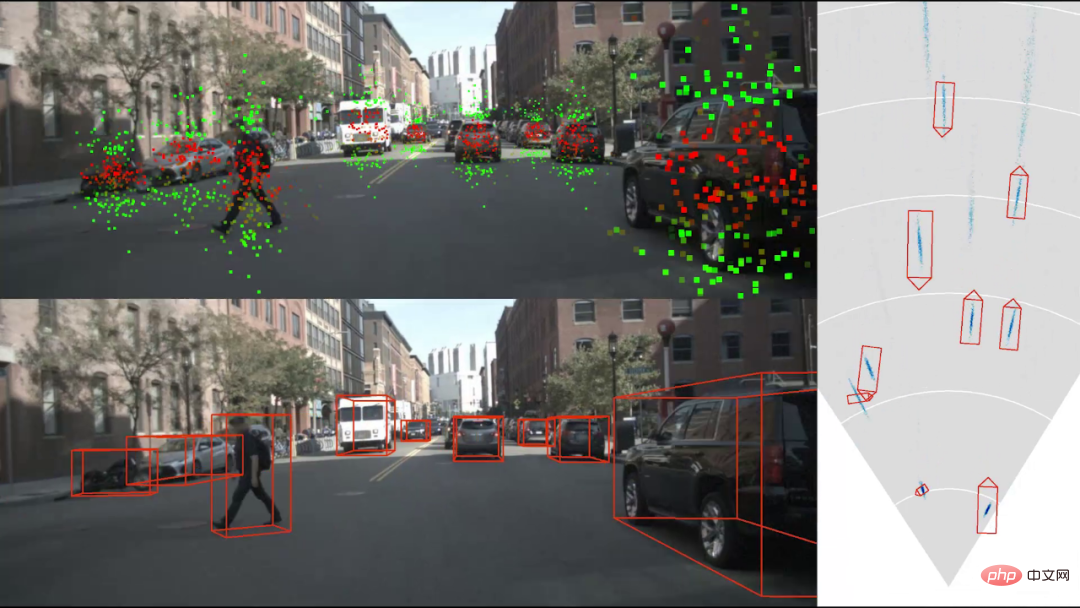
#3D ターゲット検出の結果を上の図に示します。左上の図は、変形相関ネットワークによってサンプリングされた 2D ポイントの位置を示しています。赤は水平 X 成分が高いことを示し、緑は垂直 Y 成分が高いことを示します。緑色の点は通常、オブジェクトの上端と下端にあります。その主な機能は、オブジェクトの高さからオブジェクトまでの距離を計算することです。この機能は人為的に指定されたものではなく、完全に自由なトレーニングの結果です。右の図は検出結果を上面から見たもので、青い雲の画像は物体の中心点の分布密度を表しており、物体の位置の不確実性を反映しています。一般に、遠くにある物体の位置の不確実性は、近くの物体の位置の不確実性よりも大きくなります。 
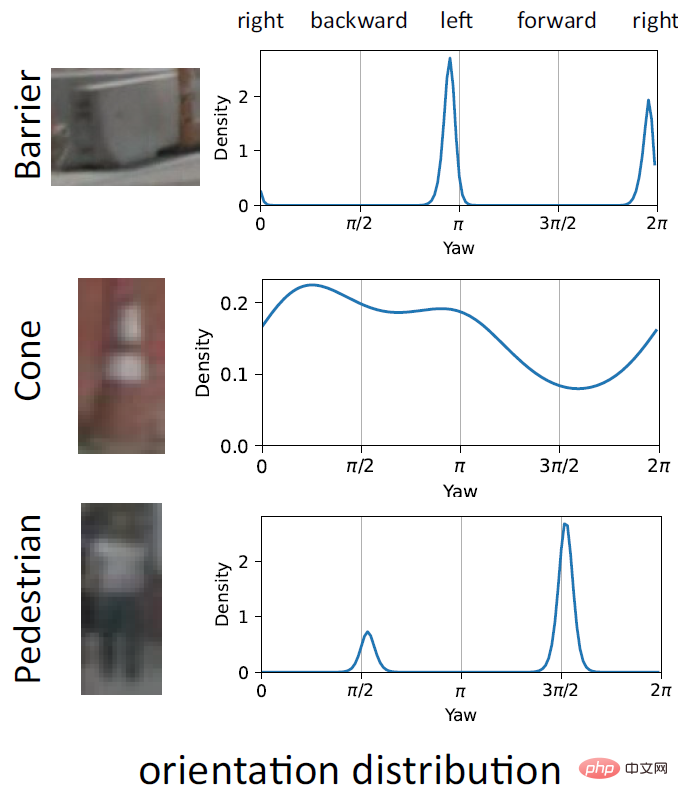
 EPro-PnP のもう 1 つの重要な利点は、複雑な多峰性分布を予測することで方向の曖昧さを表現できることです。上図に示すように、バリアはオブジェクト自体の回転対称性により、180°異なる 2 つのピークを持つことがよくあります; コーン自体には特定の方向がないため、予測結果は全方向に分布します; 歩行者は完全に回転していません左右対称ですが、画像の関係ではっきりせず、前後がわかりにくく、山が2つある場合もあります。この確率的特性により、EPro-PnP は対称オブジェクトの損失関数に特別な処理を必要としません。
EPro-PnP のもう 1 つの重要な利点は、複雑な多峰性分布を予測することで方向の曖昧さを表現できることです。上図に示すように、バリアはオブジェクト自体の回転対称性により、180°異なる 2 つのピークを持つことがよくあります; コーン自体には特定の方向がないため、予測結果は全方向に分布します; 歩行者は完全に回転していません左右対称ですが、画像の関係ではっきりせず、前後がわかりにくく、山が2つある場合もあります。この確率的特性により、EPro-PnP は対称オブジェクトの損失関数に特別な処理を必要としません。
 5. 概要
5. 概要
EPro-PnP は、本来微分不可能な最適姿勢を微分可能な姿勢確率密度に変換し、PnP 幾何最適化に基づいて位置を作成します。安定した柔軟なエンドツーエンドのトレーニング。 EPro-PnP は、一般的な 3D オブジェクトの姿勢推定問題に適用でき、3D オブジェクトの形状が不明な場合でも、エンドツーエンドのトレーニングを通じてオブジェクトの 2D-3D 関連点を学習できます。したがって、EPro-PnP は、これまで訓練することが不可能であった、私たちが提案する変形相関ネットワークなどのネットワーク設計の可能性を広げます。
さらに、EPro-PnP を直接使用して、既存の PnP ベースの姿勢推定方法を改善し、エンドツーエンドのトレーニングを通じて既存のネットワークの可能性を解放し、姿勢推定の精度を向上させることもできます。より一般的な意味では、EPro-PnP は本質的に共通分類ソフトマックスを連続領域にもたらします。幾何最適化に基づく他の 3D ビジョン問題に使用できるだけでなく、一般的な入れ子になった最適化層をトレーニングするために理論的に拡張することもできます。モデル。
以上がTongji と Alibaba の CVPR 2022 Best Student Paper Awards では何を研究しましたか?これはある作品の解釈ですの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

