
この記事は Lei Feng.com から転載されたものです。転載する必要がある場合は、Lei Feng.com の公式 Web サイトにアクセスして許可を申請してください。
最近、Andrew Ng は、自身が設立した毎週の人工知能ニュースレター「The Batch」に関するブログ投稿を更新し、機械学習の分野における複数の基本アルゴリズムの歴史的起源を要約しました。記事の冒頭で、Andrew Ng 氏は研究プロセスで下した決断を思い出しました。何年も前、あるプロジェクトでアルゴリズムを選択する際、ニューラル ネットワークと決定木学習アルゴリズムのどちらかを選択する必要がありました。計算予算を考慮して、彼は最終的にニューラル ネットワークを選択し、長い間ブーストされたデシジョン ツリーを放棄しました。これは間違った決断でしたが、「幸いなことに、私のチームはすぐに私の選択を修正し、プロジェクトは成功しました」とン氏は語った。基本的な知識を継続的に学び、更新していくことが非常に重要だと嘆いていました。他の技術分野と同様に、機械学習の分野も研究者の数が増加し、研究成果の数が増えるにつれて常に進化しています。ただし、いくつかの基本的なアルゴリズムと核となるアイデアの貢献は、時間の試練に耐えることができます:
- #アルゴリズム: 線形回帰およびロジスティック回帰、デシジョン ツリーなど
- 概念: 正則化、最適化損失関数、バイアス/分散など。
Ng の見解では、これらのアルゴリズムと概念は、多くのアイデアの中核となるものです。機械学習モデル: 住宅価格予測ツール、テキスト画像ジェネレーター (DALL・E など) などが含まれます。この最新の記事では、Ng Enda と彼のチームが 6 つの基本アルゴリズムの起源、使用、進化などを調査し、より詳細な説明を提供しました。 6 つのアルゴリズムは、線形回帰、ロジスティック回帰、勾配降下法、ニューラル ネットワーク、デシジョン ツリー、および K 平均法クラスタリング アルゴリズムです。
1 線形回帰: 直線的で狭い線形回帰は機械学習における重要な統計手法ですが、戦わずして勝つことはできません。この問題は 2 人の優れた数学者によって提案されましたが、200 年経った今でもこの問題は未解決のままです。長年にわたる論争は、このアルゴリズムの顕著な有用性だけでなく、その本質的な単純性も示しています。
では、線形回帰は誰のアルゴリズムなのでしょうか? 1805 年、フランスの数学者アドリアン マリー ルジャンドルは、彗星の位置を予測する際に一連の点に直線を当てはめる方法を発表しました (天体航法は当時の世界貿易において最も価値のある科学的方向性であり、今日の人工知能とよく似ています) ) 頭いい)。

キャプション: アドリアン=マリー・ルジャンドルのスケッチ肖像画4 年後、24 年目の- ドイツの天才カール・フリードリヒ・ガウスは、1795 年からそれを使用していると主張しましたが、それについて書くにはあまりにも些細なことだと考えていました。ガウスの主張を受けて、ルジャンドルは「非常に有名な幾何学者がためらうことなくこの方法を採用した」という匿名の記事を発表しました。フリードリヒ・ガウス
傾きとバイアス : 結果とそれに影響を与える変数の間の関係が直線に従う場合、線形回帰は単純であり、機能します。たとえば、車の燃料消費量は重量と直線的に関係します。
: 結果とそれに影響を与える変数の間の関係が直線に従う場合、線形回帰は単純であり、機能します。たとえば、車の燃料消費量は重量と直線的に関係します。
- 車の燃料消費量 y とその重量 x の関係は、直線の傾き w (重量に応じて燃料消費量が増加する程度) とオフセット項 b (燃料重量ゼロでの消費量): y=w *x b.
- トレーニング中に、アルゴリズムは車の重量を考慮して予想される燃料消費量を予測します。予想燃費と実際の燃費を比較します。次に、通常は通常の最小二乗法によって w と b の値を磨き、二乗の差を最小化します。
- 車の抗力を考慮すると、より正確な予測を生成できます。追加の変数は、線を平面まで延長します。このように、線形回帰は任意の数の変数/次元に対応できます。
普及への 2 つのステップ: このアルゴリズムは、ナビゲーターが星を追跡するのにすぐに役立ち、その後の生物学者 (特にチャールズ ダーウィンのいとこであるフランシス ゴルトン) が遺伝形質を特定しました。植物や動物において。これら 2 つのさらなる開発により、線形回帰の幅広い可能性が解き放たれました。 1922 年、英国の統計学者ロナルド フィッシャーとカール ピアソンは、線形回帰が相関と分布の一般的な統計的枠組みにどのように適合し、あらゆる科学で役立つかを示しました。そして、ほぼ 1 世紀後、コンピューターの出現により、データをさらに活用するためのデータと処理能力が提供されました。
曖昧さへの対処: もちろん、データが完全に測定されることはなく、一部の変数は他の変数よりも重要です。これらの人生の事実は、より複雑なバリエーションを引き起こします。たとえば、正則化を伴う線形回帰 (リッジ回帰とも呼ばれます) は、線形回帰モデルが 1 つの変数にあまり依存せず、むしろ最も重要な変数に均等に依存するように促します。簡単にするために、別の形式の正則化 (L2 の代わりに L1) を使用すると、できるだけ多くの係数がゼロになるように促す投げ縄 (圧縮推定値) が生成されます。言い換えれば、予測力の高い変数を選択し、残りを無視することを学習します。エラスティック ネットワークは、これら 2 種類の正則化を組み合わせます。データがまばらな場合、または特徴が関連していると思われる場合に便利です。
すべてのニューロンで : 現在、単純なバージョンは依然として非常に便利です。ニューラル ネットワーク内の最も一般的なタイプのニューロンは線形回帰モデルで、次に非線形活性化関数が続き、線形回帰が深層学習の基本コンポーネントとなっています。
2 ロジスティック回帰: 曲線に従う
ロジスティック回帰は 1 つのことを分類するためにのみ使用されていた時代がありました。つまり、毒の瓶を飲んだ場合、あなたは危険です。 「生きている」または「死んでいる」というラベルを付けることは可能ですか?時代は変わり、今日では、緊急サービスに電話することでこの質問に対するより良い答えが得られるだけでなく、ロジスティック回帰もディープラーニングの中核となっています。
毒コントロール: ロジスティック関数の起源は 1830 年代に遡り、ベルギーの統計学者 P.F. フェルフルストが人口動態を説明するために発明しました。時間の経過に伴う指数関数的な増加です。利用可能なリソースが消費されると成長は横ばいになり、特徴的なロジスティック曲線が生成されます。 1 世紀以上後、アメリカの統計学者 E. B. ウィルソンとその教え子ジェーン ウースターは、特定の有害物質がどれだけ致死的であるかを計算するロジスティック回帰を考案しました。

#キャプション: P.F. Verhulstフィッティング関数: ロジスティック回帰特定のイベント (ストリキニーネの摂取など) に対する特定の結果 (早期死亡など) の確率を予測するために、データセットにロジスティック関数を適用します。
- トレーニングでは、曲線の中心位置を水平方向に、曲線の中心位置を垂直方向に調整して、関数の出力とデータの間の誤差を最小限に抑えます。
- 中央を右または左に調整すると、普通の人を殺すのに多かれ少なかれ毒が必要になることを意味します。急な坂道は確実性を暗示しており、中間点まではほとんどの人が生き残るが、中間点を超えると「さよならを言うだけ」(死を意味する)となる。緩やかな傾斜の方が寛容です。曲線の中央より下では半分以上が生き残りますが、それより上では半分未満が生き残ります。
- ある結果と別の結果の間にしきい値 (たとえば 0.5) を設定すると、曲線が分類子になります。モデルに線量を入力するだけで、パーティーを計画すべきか葬儀を計画すべきかがわかります。
その他の結果: Verhulst の研究では、中毒被害者が死後の世界のどちら側に入る可能性があるかなどのさらなる可能性を無視して、二項対立の結果の確率を発見しました。彼の後継者はアルゴリズムを拡張しました:
- 1960 年代後半、英国の統計学者デイビッド コックスとオランダの統計学者アンリ タイルは、独立して研究し、2 つ以上の結果が考えられる状況に対してロジスティック回帰を実施しました。
- さらなる作業の結果、順序付きロジスティック回帰が得られ、結果は順序付けされた値になります。
- 疎データまたは高次元データを処理するために、ロジスティック回帰は線形回帰と同じ正則化手法を活用できます。

#イラスト: David Cox多関数曲線 : ロジスティック関数は広範囲の現象をかなりの精度で記述するため、ロジスティック回帰は多くの状況で有用なベースライン予測を提供します。医学では、死亡率と病気のリスクを推定します。政治学では、選挙の勝者と敗者を予測します。経済学では、ビジネスの見通しを予測します。さらに重要なのは、さまざまなニューラル ネットワーク内のニューロンのサブセットを駆動することです (非線形性はシグモイド関数です)。
3 勾配降下: すべてが下り坂になる夕暮れ後に山をハイキングしていて、下に何も見えなくなったことを想像してください。携帯電話のバッテリーが切れているため、GPS アプリを使って家に帰る道を見つけることもできません。勾配降下法によって最速のパスが見つかる可能性があります。崖から落ちないように注意してください。 太陽とカーペット: 急勾配の降下は、急峻な地形を下るよりも有利です。 1847 年、フランスの数学者オーギュスタン ルイ コーシーは、恒星の軌道を近似するアルゴリズムを発明しました。 60 年後、彼の同胞であるジャック アダマールは、ひざまずいてハイキングを容易にするカーペットなどの薄くて柔軟な物体の変形を記述するためにこの理論を独自に開発しました。ただし、機械学習では、学習アルゴリズムの損失関数の最低点を見つけるために最も一般的に使用されます。

キャプション: オーギュスタン=ルイ・コーシー降りる: 訓練されたニューラル ネットワークは、入力が与えられた場合に必要な出力を計算する関数を提供します。ネットワークをトレーニングする 1 つの方法は、実際の出力と目的の出力の差を繰り返し計算し、差を減らすためにネットワークのパラメーター値を変更することで、出力の損失または誤差を最小限に抑えることです。
勾配降下法は差を減らし、損失の計算に使用される関数を最小限に抑えます。ネットワークのパラメータ値は地形上の位置に相当し、損失は現在の高さになります。下に進むにつれて、目的の出力に近いものを計算するネットワークの能力を向上させることができます。典型的な教師あり学習の状況では、アルゴリズムはネットワークのパラメーター値と損失関数の勾配または傾き (つまり、自分が丘の上と下の斜面のどこにいるか) のみに依存するため、可視性は限られています。
- 基本的な方法は、地形が最も急勾配になる方向に移動することです。秘訣は、歩幅を調整することです。一歩が小さすぎると進歩するのに時間がかかり、一歩が大きすぎると未知の領域に突入し、下り坂ではなく上り坂になる可能性があります。
- 現在位置が与えられると、アルゴリズムは損失関数の勾配を計算することによって最も速い降下方向を推定します。勾配は上り坂を指しているため、アルゴリズムは勾配のわずかな部分を減算して逆方向に進みます。学習率と呼ばれる分数 α によって、勾配を再度測定する前のステップ サイズが決まります。
- これらの手順を繰り返して、谷に到達できることを願っています。おめでとう!
谷で立ち往生: アルゴリズムがおそらくあなたを山のふもとに追いやったわけではないので、携帯電話のバッテリーが切れてしまったのは残念です。複数の谷 (極小値)、山 (極大値)、鞍点 (鞍点)、および台地で構成される非凸状の地形にはまってしまうことがあります。実際、画像認識、テキスト生成、音声認識などのタスクはすべて非凸であり、この状況に対処するために勾配降下法の多くのバリエーションが登場しています。
たとえば、アルゴリズムには小さな浮き沈みを増幅させる勢いがあり、底値に到達する可能性が高くなります。研究者らは非常に多くのバリエーションを考案したため、極小値と同じ数のオプティマイザーがあるように見えました。幸いなことに、極小値と大域的極小値はほぼ等しい傾向があります。
Optimal Optimizer: 勾配降下法は、関数の最小値を見つけるための明確な選択肢です。正確な解を直接計算できる場合 (たとえば、多数の変数を使用する線形回帰タスクなど)、値を近似することができ、多くの場合、より速く、より安価になります。ただし、複雑な非線形タスクでは便利です。勾配降下と冒険心があれば、おそらく夕食までに山を出ることができるでしょう。
4 ニューラル ネットワーク: 関数の検索
最初に本題から外しましょう: 脳はグラフィックス処理装置の集合ではありません。もしそうなら、それが実行するソフトウェアは、典型的な人工ニューラル ネットワークよりもはるかに複雑です。ニューラル ネットワークは脳の構造、つまり相互接続されたニューロンの層からインスピレーションを受けており、各層は隣接するニューロンの状態に基づいて独自の出力を計算します。結果として得られる一連の活動によってアイデアが形成され、またはアイデアが認識されます。猫の写真。
生物学的から人工へ: 脳がニューロン間の相互作用を通じて学習するという考えは 1873 年に遡りますが、アメリカの神経科学者ウォーレン・マカロックとWalter Pitts は、単純な数学的規則を使用して生物学的ニューラル ネットワーク モデルを確立しました。 1958 年、アメリカの心理学者フランク ローゼンブラットは、アメリカ海軍用のハードウェア バージョンを構築することを目的として、パンチ カード マシンに実装された単層ビジュアル ネットワークであるセンサーを開発しました。

キャプション: フランク ローゼンブラット大きいほど良い: ローゼンブラットの発明は単一行の分類のみを認識できます。その後、ウクライナの数学者アレクセイ・イヴァフネンコとバレンティン・ラパは、ニューロンのネットワークを任意の数の層に積み重ねることでこの制限を克服しました。
1985 年、フランスのコンピューター科学者ヤン ルカン、デイビッド パーカー、アメリカの心理学者デイビッド ルメルハートらは、独立して研究し、そのようなネットワークを効果的に訓練するためのバックプロパゲーションの使用について説明しました。
新世紀の最初の 10 年間に、クマール チェラピラ、デイブ シュタインクラウス、ラジャット ライナ (アンドリュー ンとの共同研究) を含む研究者は、グラフィックス処理装置を使用して物事をさらに推し進めました。ニューラル ネットワークの開発。これにより、ますます大規模なニューラル ネットワークがインターネットによって生成された大量のデータから学習できるようになります。
あらゆるタスクに適しています: ニューラル ネットワークの原理は単純です。どのようなタスクにも、それを実行する関数が存在します。ニューラル ネットワークは、それぞれが 1 つのニューロンによって実行される複数の単純な関数を組み合わせて、トレーニング可能な関数を形成します。ニューロンの機能は、「重み」と呼ばれる調整可能なパラメータによって決定されます。
これらの重みと、目的の出力に対するランダムな値を含む入力例を考慮すると、トレーニング可能な関数が当面のタスクを実行するまで重みを繰り返し変更できます。
- ニューロンはさまざまな入力 (ピクセルや単語を表す数値、前の層の出力など) を受け取り、それらに重みを乗算し、その積を加算します。その結果、開発者が選択した非線形関数または活性化関数の合計が得られます。この期間中は、線形回帰に活性化関数を加えたものであると考える必要があります。
- トレーニングにより体重が変わります。入力例ごとに、ネットワークは出力を計算し、それを予想される出力と比較します。バックプロパゲーションでは、勾配降下法を通じて重みを変更し、実際の出力と予想される出力の差を減らします。このプロセスが十分な (良い) 例を使用して十分な回数繰り返されると、ネットワークはタスクの実行を学習します。
ブラック ボックス : 運が良ければ、よく訓練されたネットワークがその仕事をすることができますが、最終的には、多くの場合、次のような関数を読み取ることになります。何千もの変数とネストされた活性化関数が含まれる複雑なため、ネットワークがそのタスクをどのように成功させるかを説明するのは困難です。さらに、よく訓練されたネットワークの良さは、学習したデータによって決まります。
たとえば、データセットに偏りがある場合、ネットワークの出力にも偏りが生じます。猫の高解像度画像のみが含まれている場合、低解像度画像にどう反応するかは不明です。常識の一部: ニューヨーク・タイムズは、ローゼンブラットの 1958 年のセンサーについて報道し、「アメリカ海軍は歩き、話し、見、書き、自己複製できる機械を望んでいる」と指摘し、人工知能の誇大宣伝の先駆けとなりました。自分自身の存在を認識している電子コンピューターのプロトタイプです。」
当時のセンサーはこの要件を満たしていませんでしたが、画像用の畳み込みニューラル ネットワーク、テキスト用のリカレント ニューラル ネットワーク、音声、ビデオ、タンパク質構造などのトランスフォーマーなど、多くの印象的なモデルを生み出しました。
彼らはすでに、囲碁で人間レベルのパフォーマンスを超えたり、X線画像の診断などの実践的なタスクで人間レベルのパフォーマンスに近づいたりするなど、驚くべき成果を上げています。しかし、常識や論理的推論の観点からは、それらに対処するのはさらに困難です。
5 決定木: 根から葉まで
アリストテレスとはどのような「獣」でしょうか? 3 世紀にシリアに住んでいたこの哲学者の信奉者であるポルピュリオスは、この質問に答える論理的な方法を考え出しました。
彼は、アリストテレスが提案した「存在のカテゴリー」を一般的なものから特殊なものまで組み合わせ、アリストテレスをそれぞれの分類に順番に分類しました。無生物ではなく生物であり、彼の思考は非合理的ではなく合理的でした。
したがって、彼の分類は人間です。中世の論理学の教師は、このシーケンスを垂直方向の流れ図、つまり初期の意思決定ツリーとして描きました。
数値の違い: 1963 年に遡ると、ミシガン大学の社会学者ジョン ソンクイストと経済学者のジェームス モーガンが調査回答者をグループ化していました。コンピューターの時間。アルゴリズムを自動的にトレーニングするソフトウェアの出現により、この種の作業は一般的になり、決定木は現在、scikit-learn などのさまざまな機械学習ライブラリで使用されています。このコードは、スタンフォード大学とカリフォルニア大学バークレー校の 4 人の統計学者によって 10 年間かけて開発されました。現在、デシジョン ツリーをゼロから作成することは、機械学習 101 の宿題になっています。
空中の根っこ: デシジョン ツリーは分類または回帰を実行できます。これはルートからクラウンまで下向きに成長し、意思決定階層の入力例を 2 つ (またはそれ以上) に分類します。ドイツの医学者で人類学者のヨハン・ブルーメンバッハの話題が思い出されます: 1776 年頃、彼は初めてサルと類人猿を区別しました (人間はさておき) それ以前は、サルと類人猿は一緒に分類されていました。
この分類は、尾の有無、胸が狭いか広いか、直立しているかしゃがんでいるか、知能のレベルなど、さまざまな基準によって決まります。訓練された決定木を使用して、各基準を 1 つずつ考慮してそのような動物にラベルを付け、最終的に 2 つの動物のグループを分離します。
- ツリーは、チンパンジー、ゴリラ、オランウータンに加え、オマキザル、ヒヒ、マーモセット。ルートは、2 つの子ノードが特定の特性を示すかどうかの選択肢を提供し、その結果、2 つの子ノードにはその特性を持つ例と持たない例が含まれます。類推すると、このプロセスは任意の数のリーフ ノードで終了し、各リーフ ノードにはカテゴリの大部分またはすべてが含まれます。
- ツリーが成長するためには、ルートの決定を見つける必要があります。選択するには、すべての特徴とその価値 (後肢、バレルチェストなど) を考慮し、セグメンテーションの純度を最大化するものを選択します。 「最適な純度」は、カテゴリのインスタンスが 100% 特定の子ノードに入り、別のノードには決して入らないこととして定義されます。フォークが 1 回の決定で 100% 純粋になることはほとんどありませんし、おそらくそうなることはありません。このプロセスが続くと、より多くの特徴を考慮しても純度があまり上がらなくなるまで、次から次へとレベルの子ノードが生成されます。この時点で、ツリーは完全にトレーニングされています。
- 推論中、新しい例はデシジョン ツリーを上から下に調べ、各レベルでのさまざまな決定の評価を完了します。それが配置されているリーフ ノードに含まれるデータ ラベルを取得します。
トップ 10 に入る: 人間は広い骨盤、手、食いしばった歯によって類人猿と区別されるというブルーメンバッハの結論 (後にチャールズ ダーウィンによって覆された) を踏まえると、決定木を拡張して類人猿やサルだけでなく人間も分類したいと思いましたか?オーストラリアのコンピュータ科学者、ジョン・ロス・クインランは 1986 年に、非バイナリ結果をサポートするためにデシジョン ツリーを拡張した ID3 でこれを可能にしました。 2008 年、IEEE 国際データ マイニング会議が計画したデータ マイニング アルゴリズムのトップ 10 のリストでは、C4.5 という名前の拡張絞り込みアルゴリズムがトップにランクされました。
イノベーションが蔓延する世界において、これは持続力です。葉を剥がす: ディシジョン ツリーにはいくつかの欠点があります。 複数レベルの階層を追加して、リーフ ノードに 1 つの例のみが含まれるようにすることで、データを簡単に過学習させることができます。 さらに悪いことに、バタフライ効果が起こりやすくなります。一例を変えると、成長する木がまったく異なります。
Into the Forest: アメリカの統計学者レオ・ブライマンとニュージーランドの統計学者アデル・カトラーは、この特徴を利点に変え、2001 年にランダム フォレスト (ランダム フォレスト) を開発しました。ツリーのそれぞれが、異なる重複する例の選択を処理し、最終結果に投票します。 Random Forest とそのいとこである XGBoost は過学習の傾向が少ないため、最も人気のある機械学習アルゴリズムの 1 つとなっています。それは、アリストテレス、斑岩、ブルーメンバッハ、ダーウィン、ジェーン グドール、ダイアン 師匠、その他 1,000 人の動物学者を部屋に集めて、分類が最善であることを確認するようなものです。
6 K 平均法クラスタリング: Groupthink
パーティーで他の人と近くに立っている場合は、何か共通点がある可能性があります。これは、K 平均法クラスタリングを使用してデータ ポイントをグループ化するというアイデアです。人間の行為によって形成されたグループであっても、他の力によって形成されたグループであっても、このアルゴリズムはそれらを見つけます。 爆発からダイヤルトーンまで:ベル研究所の象徴的なイノベーションファクトリーと原子爆弾を発明したマンハッタン計画の卒業生であるアメリカの物理学者スチュアート・ロイドは、1957年にAssignで数値解析を実行するためにK平均法クラスタリングを初めて提案しました。情報は信号に含まれていますが、この研究は 1982 年まで出版されませんでした:

論文アドレス: https://cs.nyu.edu / ~roweis/csc2515-2006/readings/lloyd57.pdf一方、アメリカの統計学者エドワード フォーギーは 1965 年に同様のアプローチを説明し、その別名「ロイド フォーギー アルゴリズム」につながりました。 センターの検索: クラスターを同じ考えを持つ作業グループに分割することを検討してください。室内の参加者の位置と形成するグループの数を考慮すると、K 平均法クラスタリングでは参加者をほぼ同じサイズのグループに分割し、各グループが中心点または重心の周りにクラスター化されます。
- #トレーニング中、アルゴリズムは最初に k 人をランダムに選択することで k 個の重心を指定します。 (K は手動で選択する必要があり、最適な値を見つけることが場合によっては非常に重要です。) 次に、各人物を最も近い重心に関連付けることにより、k 個のクラスターを成長させます。
- クラスターごとに、そのグループに割り当てられたすべての人の平均位置を計算し、その平均位置を新しい重心として割り当てます。新しい重心はそれぞれ人によって占有されるわけではないかもしれませんが、それではどうでしょうか?チョコレートやフォンデュの周りには人が集まります。
- 新しい重心を計算した後、アルゴリズムは個人を最も近い重心に再割り当てします。次に、新しい重心を計算し、重心 (およびその周囲のグループ) が動かなくなるまでクラスターを調整します。その後、新しいメンバーを正しいクラスターに割り当てるのは簡単です。それらを部屋の所定の位置に配置し、最も近い重心を探します。
- あらかじめ警告してください。最初に重心がランダムに割り当てられると、あなたが一緒にいたいと思っている愛すべきデータ中心の AI 専門家と同じグループにならない可能性があります。このアルゴリズムは適切に機能しますが、最適な解決策が見つかるとは限りません。
異なる距離: もちろん、クラスター化されたオブジェクト間の距離は大きくする必要はありません。 2 つのベクトル間の任意のメトリックが使用可能です。たとえば、K 平均法クラスタリングでは、パーティー参加者を物理的な距離に基づいてグループ化するのではなく、服装、職業、その他の属性に基づいて分類できます。オンライン ストアはこれを使用して顧客の好みや行動に基づいてセグメントを分類し、天文学者は同じ種類の星をグループ化することができます。 データポイントの力: このアイデアはいくつかの重要な変化をもたらしました:
- K-medoids 特定のクラスター内の平均位置ではなく、実際のデータ ポイントを重心として使用します。中心点は、クラスター内のすべての点までの距離を最小にする点です。重心が常にデータ ポイントであるため、この変化は解釈しやすくなります。
- ファジー C 平均法クラスタリング データ ポイントがさまざまな程度で複数のクラスターに参加できるようにします。これは、ハード クラスターの割り当てを、重心からの距離に基づいたクラスター次数に置き換えます。
n 次元のカーニバル: それにもかかわらず、元の形式のアルゴリズムは依然として広く有用です。特に教師なしアルゴリズムとして、高価な収集を必要としないためです。ラベル付きデータ。また、使用頻度もますます高まっています。たとえば、scikit-learn を含む機械学習ライブラリは、2002 年に高次元データを非常に迅速に分割できる kd ツリーの追加の恩恵を受けました。
以上がAndrew Ng: 機械学習の 6 つのコア アルゴリズムの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 AIのスキルギャップは、サプライチェーンのダウンを遅くしていますApr 26, 2025 am 11:13 AM
AIのスキルギャップは、サプライチェーンのダウンを遅くしていますApr 26, 2025 am 11:13 AM「AI-Ready労働力」という用語は頻繁に使用されますが、サプライチェーン業界ではどういう意味ですか? サプライチェーン管理協会(ASCM)のCEOであるAbe Eshkenaziによると、批評家ができる専門家を意味します
 1つの会社がAIを永遠に変えるために静かに取り組んでいる方法Apr 26, 2025 am 11:12 AM
1つの会社がAIを永遠に変えるために静かに取り組んでいる方法Apr 26, 2025 am 11:12 AM分散型AI革命は静かに勢いを増しています。 今週の金曜日、テキサス州オースティンでは、ビテンサーのエンドゲームサミットは極めて重要な瞬間を示し、理論から実用的な応用に分散したAI(DEAI)を移行します。 派手なコマーシャルとは異なり
 Nvidiaは、AIエージェント開発を合理化するためにNEMOマイクロサービスをリリースしますApr 26, 2025 am 11:11 AM
Nvidiaは、AIエージェント開発を合理化するためにNEMOマイクロサービスをリリースしますApr 26, 2025 am 11:11 AMエンタープライズAIはデータ統合の課題に直面しています エンタープライズAIの適用は、ビジネスデータを継続的に学習することで正確性と実用性を維持できるシステムを構築する大きな課題に直面しています。 NEMOマイクロサービスは、NVIDIAが「データフライホイール」と呼んでいるものを作成することにより、この問題を解決し、AIシステムがエンタープライズ情報とユーザーインタラクションへの継続的な露出を通じて関連性を維持できるようにします。 この新しく発売されたツールキットには、5つの重要なマイクロサービスが含まれています。 NEMOカスタマイザーは、より高いトレーニングスループットを備えた大規模な言語モデルの微調整を処理します。 NEMO評価者は、カスタムベンチマークのAIモデルの簡素化された評価を提供します。 Nemo Guardrailsは、コンプライアンスと適切性を維持するためにセキュリティ管理を実装しています
 aiは芸術とデザインの未来のために新しい絵を描きますApr 26, 2025 am 11:10 AM
aiは芸術とデザインの未来のために新しい絵を描きますApr 26, 2025 am 11:10 AMAI:芸術とデザインの未来 人工知能(AI)は、前例のない方法で芸術とデザインの分野を変えており、その影響はもはやアマチュアに限定されませんが、より深く影響を与えています。 AIによって生成されたアートワークとデザインスキームは、広告、ソーシャルメディアの画像生成、Webデザインなど、多くのトランザクションデザインアクティビティで従来の素材画像とデザイナーに迅速に置き換えられています。 ただし、プロのアーティストやデザイナーもAIの実用的な価値を見つけています。 AIを補助ツールとして使用して、新しい美的可能性を探求し、さまざまなスタイルをブレンドし、新しい視覚効果を作成します。 AIは、アーティストやデザイナーが繰り返しタスクを自動化し、さまざまなデザイン要素を提案し、創造的な入力を提供するのを支援します。 AIはスタイル転送をサポートします。これは、画像のスタイルを適用することです
 エージェントAIとのズームがどのように革命を起こしているか:会議からマイルストーンまでApr 26, 2025 am 11:09 AM
エージェントAIとのズームがどのように革命を起こしているか:会議からマイルストーンまでApr 26, 2025 am 11:09 AM最初はビデオ会議プラットフォームで知られていたZoomは、エージェントAIの革新的な使用で職場革命をリードしています。 ZoomのCTOであるXD Huangとの最近の会話は、同社の野心的なビジョンを明らかにしました。 エージェントAIの定義 huang d
 大学に対する実存的な脅威Apr 26, 2025 am 11:08 AM
大学に対する実存的な脅威Apr 26, 2025 am 11:08 AMAIは教育に革命をもたらしますか? この質問は、教育者と利害関係者の間で深刻な反省を促しています。 AIの教育への統合は、機会と課題の両方をもたらします。 Tech Edvocate NotesのMatthew Lynch、Universitとして
 プロトタイプ:アメリカの科学者は海外の仕事を探していますApr 26, 2025 am 11:07 AM
プロトタイプ:アメリカの科学者は海外の仕事を探していますApr 26, 2025 am 11:07 AM米国における科学的研究と技術の開発は、おそらく予算削減のために課題に直面する可能性があります。 Natureによると、海外の雇用を申請するアメリカの科学者の数は、2024年の同じ期間と比較して、2025年1月から3月まで32%増加しました。以前の世論調査では、調査した研究者の75%がヨーロッパとカナダでの仕事の検索を検討していることが示されました。 NIHとNSFの助成金は過去数か月で終了し、NIHの新しい助成金は今年約23億ドル減少し、3分の1近く減少しました。リークされた予算の提案は、トランプ政権が科学機関の予算を急激に削減していることを検討しており、最大50%の削減の可能性があることを示しています。 基礎研究の分野での混乱は、米国の主要な利点の1つである海外の才能を引き付けることにも影響を与えています。 35
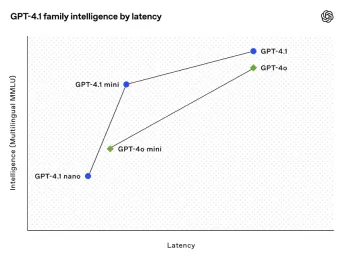 オープンAIの最新のGPT 4.1ファミリ - 分析VidhyaApr 26, 2025 am 10:19 AM
オープンAIの最新のGPT 4.1ファミリ - 分析VidhyaApr 26, 2025 am 10:19 AMOpenaiは、強力なGPT-4.1シリーズを発表しました。実際のアプリケーション向けに設計された3つの高度な言語モデルのファミリー。 この大幅な飛躍は、より速い応答時間、理解の強化、およびTと比較した大幅に削減されたコストを提供します


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

WebStorm Mac版
便利なJavaScript開発ツール

mPDF
mPDF は、UTF-8 でエンコードされた HTML から PDF ファイルを生成できる PHP ライブラリです。オリジナルの作者である Ian Back は、Web サイトから「オンザフライ」で PDF ファイルを出力し、さまざまな言語を処理するために mPDF を作成しました。 HTML2FPDF などのオリジナルのスクリプトよりも遅く、Unicode フォントを使用すると生成されるファイルが大きくなりますが、CSS スタイルなどをサポートし、多くの機能強化が施されています。 RTL (アラビア語とヘブライ語) や CJK (中国語、日本語、韓国語) を含むほぼすべての言語をサポートします。ネストされたブロックレベル要素 (P、DIV など) をサポートします。

EditPlus 中国語クラック版
サイズが小さく、構文の強調表示、コード プロンプト機能はサポートされていません

DVWA
Damn Vulnerable Web App (DVWA) は、非常に脆弱な PHP/MySQL Web アプリケーションです。その主な目的は、セキュリティ専門家が法的環境でスキルとツールをテストするのに役立ち、Web 開発者が Web アプリケーションを保護するプロセスをより深く理解できるようにし、教師/生徒が教室環境で Web アプリケーションを教え/学習できるようにすることです。安全。 DVWA の目標は、シンプルでわかりやすいインターフェイスを通じて、さまざまな難易度で最も一般的な Web 脆弱性のいくつかを実践することです。このソフトウェアは、

SublimeText3 英語版
推奨: Win バージョン、コードプロンプトをサポート!

ホットトピック
 7733
7733 15
15 1643
1643 14
14 1397
1397 52
52 1290
1290 25
25 1233
1233 29
29


 : 結果とそれに影響を与える変数の間の関係が直線に従う場合、線形回帰は単純であり、機能します。たとえば、車の燃料消費量は重量と直線的に関係します。
: 結果とそれに影響を与える変数の間の関係が直線に従う場合、線形回帰は単純であり、機能します。たとえば、車の燃料消費量は重量と直線的に関係します。 
