ホームページ >テクノロジー周辺機器 >AI >VAE表現学習の問題を解決するために、北海道大学は新しい生成モデルGWAEを提案しました
VAE表現学習の問題を解決するために、北海道大学は新しい生成モデルGWAEを提案しました
- 王林転載
- 2023-04-07 17:47:331892ブラウズ
高次元データの低次元表現の学習は、教師なし学習の基本的なタスクです。そのような表現はデータの本質を簡潔に捉えており、低次元の入力に基づいた下流タスクの実行を可能にするためです。可能です。変分オートエンコーダ (VAE) は重要な表現学習方法ですが、その客観的な制御のため、表現学習は依然として困難な作業です。 VAE の証拠下限 (ELBO) 目標は生成的にモデル化されていますが、学習表現はこの目標を直接ターゲットにしていないため、もつれの解除など、表現学習タスクに対する特定の修正が必要です。これらの変更はモデルに暗黙的な望ましくない変更をもたらす場合があり、制御された表現の学習が困難なタスクになります。
変分オートエンコーダにおける表現学習問題を解決するために、この論文では Gromov-Wasserstein Autoencoders (GWAE) と呼ばれる新しい生成モデルを提案します。 GWAE は、変分オートエンコーダー (VAE) モデル アーキテクチャに基づいた表現学習のための新しいフレームワークを提供します。データ変数の生成モデリングのための従来の VAE ベースの表現学習方法とは異なり、GWAE はデータと潜在変数間の最適な転送を通じて有益な表現を取得します。 Gromov-Wasserstein (GW) メトリックは、考慮中の変数の距離構造に焦点を当てた、比較できない変数 (たとえば、異なる次元を持つ変数) 間のこのような最適な転送を可能にします。 ELBO 目標を GW メトリックに置き換えることにより、GWAE はデータと潜在空間の間の比較を実行し、変分オートエンコーダーでの表現学習を直接ターゲットにします (図 1)。この表現学習の定式化により、学習された表現は、メタ事前条件と呼ばれる、有益と考えられる特定の特性 (分解可能性など) を持つことができます。
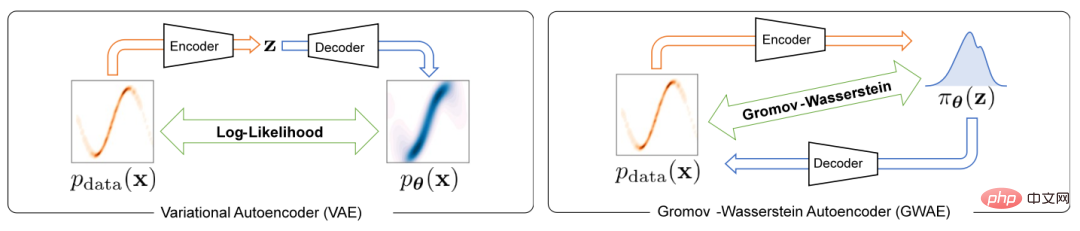
図 1 VAE と GWAE の違い
##この研究では、 ICLR 2023 に大幅に承認されました。
- #紙のリンク: https://arxiv.org/abs/2209.07007
- コードリンク: https://github.com/ganmodokix/gwae
- メソッドの紹介
データ配布と潜在的な事前配布の間 GW ターゲット
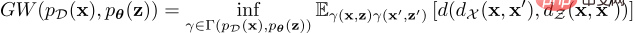 この最適伝送コストの公式は、比類のない空間における分布の不一致を測定できますが、連続的な分布の場合、それは次のように定義されます。すべての結合を下限にする必要があるため、正確な GW 値を計算することは非現実的です。この問題を解決するために、GWAE は緩和された最適化問題を解き、GW 推定量を推定して最小化します。その勾配は自動微分によって計算できます。緩和ターゲットは、推定された GW メトリックと 3 つの正則化損失の合計であり、これらはすべて PyTorch などの微分可能なプログラミング フレームワークで実装できます。この緩和目標は、主損失と 3 つの正則化損失、つまり主推定 GW 損失、WAE ベースの再構成損失、結合十分条件損失、およびエントロピー正則化損失で構成されます。
この最適伝送コストの公式は、比類のない空間における分布の不一致を測定できますが、連続的な分布の場合、それは次のように定義されます。すべての結合を下限にする必要があるため、正確な GW 値を計算することは非現実的です。この問題を解決するために、GWAE は緩和された最適化問題を解き、GW 推定量を推定して最小化します。その勾配は自動微分によって計算できます。緩和ターゲットは、推定された GW メトリックと 3 つの正則化損失の合計であり、これらはすべて PyTorch などの微分可能なプログラミング フレームワークで実装できます。この緩和目標は、主損失と 3 つの正則化損失、つまり主推定 GW 損失、WAE ベースの再構成損失、結合十分条件損失、およびエントロピー正則化損失で構成されます。
このスキームは、事前分布を柔軟にカスタマイズして、低次元表現に有益な特徴を導入することもできます。具体的には、この論文では次の 3 つの事前集団を紹介しています。
Neural Priori (NP) In GWAEs with NP、完全に接続されたニューラル ネットワークは、アプリオリ サンプラーを構築するために使用されます。この事前分布ファミリーは、基礎となる変数に関する仮定が少なく、一般的な状況に適しています。
因数分解ニューラル事前分布 (FNP)FNP を使用した GWAE では、ローカルに接続されたニューラル事前分布を使用します。ネットワークは、各潜在変数のエントリが独立して生成されるサンプラー。このサンプラーは、因数分解された事前表現と用語に依存しない表現を生成します。これは、代表的なメタ事前分散の優れた方法です。
ガウス混合事前分布 (GMP) GMP では、複数のガウス分布の混合として定義され、そのサンプラーは重度のガウス分布を使用できます。パラメータ化手法と Gumbel-Max 手法が実装されています。 GMP では、事前分布の各ガウス成分がクラスターを捕捉すると予想される表現でクラスターを仮説化することができます。
実験と結果
この研究では、GWAE の 2 つの主要なメタ事前実証的評価を実施しました:ソリューション エンタングルメントとクラスタリング。
解絡 研究では、3D Shapes データセットと DCI メトリクスを使用して、GWAE の解絡能力を測定しました。結果は、FNP を使用した GWAE が単一軸上でオブジェクトの色相因子を学習できることを示しており、これは GWAE のもつれを解く能力を実証しています。定量的評価によっても、GWAE の解絡性能が実証されます。
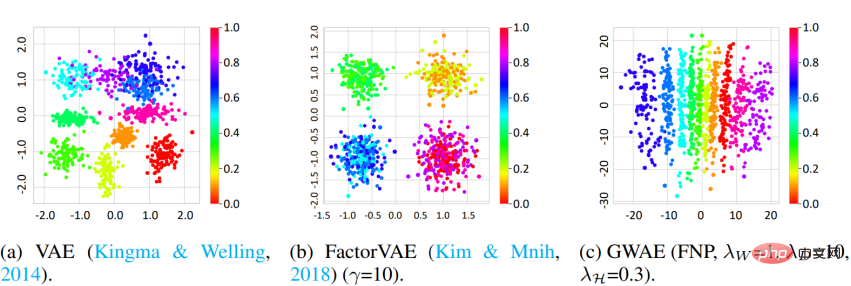
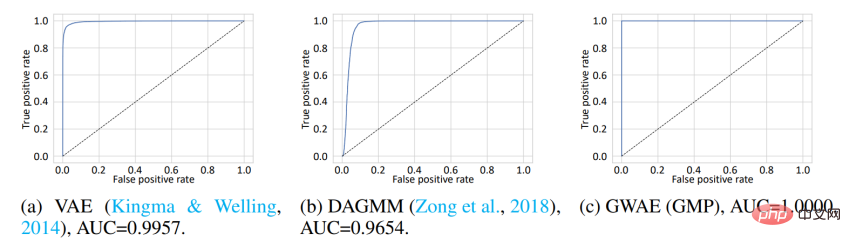
クラスタリング クラスタリング要素の事前確率に基づいて得られた表現を評価するために、研究では、アウト・オブ・分布 (OOD) 検出。 MNIST データセットは In-Distribution (ID) データとして使用され、Omniglot データセットは OoD データとして使用されます。 MNIST には手書きの数字が含まれていますが、Omniglot には異なる文字の手書き文字が含まれています。この実験では、ID データセットと OoD データセットは手書き画像のドメインを共有していますが、異なる文字が含まれています。モデルは ID データでトレーニングされ、学習した表現を使用して ID または OoD データを検出します。 VAE と DAGMM では、OoD 検出に使用される変数は事前対数尤度ですが、GWAE ではカントロビッチ ポテンシャルです。 GWAE の事前分布は、MNIST のクラスターをキャプチャするために GMP を使用して構築されました。 ROC 曲線はモデルの OoD 検出パフォーマンスを示しており、3 つのモデルすべてがほぼ完璧なパフォーマンスを達成していますが、曲線下面積 (AUC) に関しては GMP を使用して構築された GWAE が最も優れたパフォーマンスを示しました。
さらに、この研究では GWAE の生成能力も評価しました。
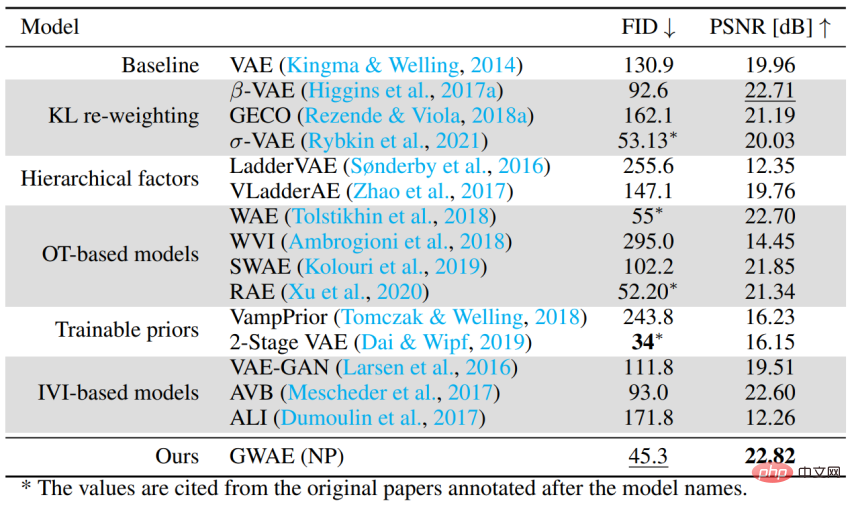
オートエンコーダベースの生成モデルとしてのパフォーマンス 特定のメタ事前条件なしで一般的なケースを処理する GWAE の能力を評価するために、CelebA データが使用されます。発電性能を評価した。この実験では、FID を使用してモデルの生成パフォーマンスを評価し、PSNR を使用して自動エンコーディングのパフォーマンスを評価します。 GWAE は、NP を使用して 2 番目に優れた生成パフォーマンスと最高の自動エンコーディング パフォーマンスを達成し、モデル内のデータ分布をキャプチャし、その表現でデータ情報をキャプチャできる能力を実証しました。
概要
- GWAE は、Gromov-Wasserstein 計量に基づいて構築された変分オートエンコーダ生成モデルであり、直接的な目標を達成することを目的としています。表現学習。
- 事前分布は微分可能なサンプルのみを必要とするため、メタ事前分布 (表現の理想的な特性) を仮定するためにさまざまな事前分布設定を構築できます。
- プライマリ メタ プリアの実験と変分オートエンコーダとしてのパフォーマンス評価は、GWAE 定式化の柔軟性と GWAE の表現学習機能を示しています。
- 筆頭著者 中川直の個人ホームページ: https://ganmodokix.com/note/cv
- # #北海道大学マルチメディア研究室ホームページ:https://www-lmd.ist.hakudai.ac.jp/
以上がVAE表現学習の問題を解決するために、北海道大学は新しい生成モデルGWAEを提案しましたの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

