
1. なぜ因果関係を気にするのか
まず、因果関係とは何かを紹介しましょう:

いつ「変数/イベント間には関係がある」と言いますが、これは変数/イベントが独立していないことを意味しており、変数/イベント間には何らかの関係があるはずです。ただし、X が Y の「原因」であるという意味は、特定の方法を使用して Different を変更する場合に意味します。ここでの介入はランダムではなく、ターゲット変数の非常に正確な直接制御 (「雨が降る」を直接変更する) であることに注意してください。この変更はシステム内の他の変数に直接影響しません。同時に、この方法、つまり人間による直接の介入によって、ある変数が別の変数の直接の原因であるかどうかを判断することもできます。

因果関係を分析する必要性の例を以下に示します。
① 典型的なケースは、肺疾患と爪の色が喫煙によって存在することです。これと関係があるのは、紙巻きタバコにはフィルターがないため、定期的に吸うと爪が黄色くなり、また喫煙は肺疾患を引き起こす可能性があるということです。特定の領域の肺疾患の発生率を変えたい場合、爪を漂白するだけでは改善できません。肺疾患の依存性を変えるのではなく、肺疾患の原因を見つける必要があります。肺疾患の発生率を変えるという目標を達成するには、因果関係の分析が必要です。
② 2 番目のケースは、シンプソンのパラドックスです。上の図の右側は実際のデータ セットです。このデータ セットには、腎臓結石の 2 セットのデータが示されています。1 つのグループには小さな結石があり、もう 1 つのグループには大きな結石があり、さらに 2 つの治療法 A と B があります。表からわかるように、小さな結石グループと大きな結石グループに関係なく、治療法 A の方が治癒率が 93%、73% と良好であり、治療法 B の治癒率はそれぞれ87%と69%。しかし、同じ治療法を受けた結石患者の 2 つのグループを混合した場合、治療計画 B (83%) の全体的な効果は治療計画 A (78%) よりも優れていました。あなたが治癒率、つまり新患の治療計画をどのように選択するかだけを気にする医師であると仮定します。その理由は、推奨を行う際に、治療と治癒の間の因果関係のみを考慮し、他の依存関係については考慮していないためです。しかし、結石の大きさは治療と治るかどうかの共通の原因であり、治療と治癒の依存度の量的な変化につながります。したがって、治療法と治癒の関係を研究する場合には、依存関係ではなく、前者と後者の因果関係を議論する必要があります。
③ 3 番目のケース: 50 年前の統計では、大学に通う女性は平均して男性よりも賢かったことが示されていましたが、実際には大きな差はないはずです。女性は男性に比べて大学入学が難しいため、学校が生徒を募集する際に性別や試験の能力などの影響を受けるという選抜バイアスが存在します。 「結果」が生じた場合、性別と受験能力には何らかの関係が生じます。インターネットから収集されたデータを使用する場合にも、選択バイアスの問題が存在します。データ ポイントが収集されたかどうかと特定の属性の間には関係があることが多く、インターネット上に置かれたデータのみを分析する場合は、これらの要素に注意する必要があります。これが実現すると、選択バイアスのあるデータも因果関係から解析でき、集団そのものの性質を復元・推測することが可能になります。

上の図は、いくつかの機械学習/深層学習の問題を示しています。
① ほとんどの予測はデータの分布に関連していることがわかっています。たとえば転移学習では、アフリカからアメリカ大陸にモデルを転送しても最適な予測を行いたい場合、明らかに、さまざまなデータ分布に基づいてモデルを適応的に調整する必要があります。このとき、データの分布にどのような変化が生じ、どのように変化したかを分析することが特に重要です。データの何が変更されたかを知ることで、それに応じてモデルを調整できます。別の例として、病気を診断する AI モデルを構築する場合、機械が提示する診断結果に満足できず、どの変異が病気の原因であるかなど、機械がなぜそのような結論に至ったのかをさらに知りたくなるでしょう。さらに、病気をどのように治療するかについては、多くの「なぜ」という疑問が生じます。同様に、レコメンデーション システムがレコメンデーションを行う場合、そのアイテムや戦略を推奨する理由を知りたいと思うでしょう。たとえば、企業は単に収益を増やしたいだけなのか、そのアイテムや戦略がユーザーに適しているのか、そのアイテムや戦略は適切ではないのかなどです。将来にとって有益です。これらの「なぜ」の質問はすべて原因と結果の質問です。
② ディープラーニングの分野には、敵対的攻撃という概念があります。図に示すように、左側のジャイアントパンダの写真に特定のノイズを追加したり、特定のピクセルを変更したりすると、機械はその写真をジャイアントパンダではなく他の種類の動物であると判断し、その信頼度はまだ非常に高いです。しかし人間にとって、この2枚の写真は明らかにジャイアントパンダです。これは、現在機械が画像から学習している高レベルの特徴が、人間が学習している高レベルの特徴と一致しないためです。マシンが使用する高レベルの機能が人間の機能と一致しない場合、敵対的な攻撃が発生する可能性があります。入力が変わると人間や機械の判断も変わり、最終的な判断結果に問題が生じます。人間と一貫性のある高レベルの機能を機械に学習させること、つまり、機械が人間と同じ方法で機能を学習して使用できるようにすることによってのみ、敵対的な攻撃を回避することができます。

なぜ因果表現を行う必要があるのでしょうか?
① 下流のタスクに利益をもたらす: たとえば、下流の分類やその他のタスクのパフォーマンスを向上させるのに役立ちます。
② 「なぜ」の質問を説明できる。
③ データの背後にある本当の因果的特徴を回復する: 哲学におけるカントの形而上学では、人間が経験する世界は経験的な世界であると考えられています。それは背後にある世界そのものに基づいていますが、私たちは世界の存在論を直接認識することはできず、時間、空間、因果関係などのいくつかの特性が感覚システムによって経験世界に自動的に追加されています。したがって、人間と一致する特徴を機械に学習させたい場合は、機械が因果関係、因果関係、時間、空間などの特徴を学習する能力を備えている必要があります。
2. 因果表現学習: 独立かつ同一分布の状況
1. 因果表現学習の基本概念
独立かつ同一分布の状況で因果関係を学習するにはどうすればよいでしょうか?まず、2 つの質問に答える必要があります。1 つ目は、データ内のどのようなプロパティが因果関係に関連しているのか、もう 1 つはデータ内にどのような手がかり (「フットプリント」) があるのかということです。 2つ目は、データの取得条件において因果関係が復元できるかどうか、すなわち因果関係系の特定可能性の問題である。

因果システムの最も重要な特性は「モジュール性」です。システム内の変数には特定の関係がありますが、システムは因果関係に分割できます。複数のサブシステム ( 1 つの原因が 1 つの従属変数を生成します)。たとえば、「雨が降っている」、「地面が濡れている」、「地面が滑りやすい」は相互依存しており、因果関係によって「何らかの理由で雨が降る」、「何らかの理由で雨が降る」という 3 つのサブシステムに分けることができます。 「地面が濡れている」、「地面が濡れていると滑りやすくなります。」変数間には依存関係がありますが、これら 3 つのプロセス (サブシステム) は接続されておらず、パラメーターの共有もなく、一方のシステムの変更が他方のシステムに変更を引き起こすことはありません。たとえば、特定の物質を散布して「地面が濡れて滑りやすくなる」という効果を変えることは、雨が降るか降らないかには影響せず、雨が降って地面が濡れていることの影響も変わりません。この特性は「モジュール性」と呼ばれます。これは、システムが因果関係の観点から異なるサブモジュールに分割されており、サブモジュール間に接続がないことを意味します。
モジュール性から始めて、因果システムの 3 つのプロパティを取得できます:
① 変数間の条件付き独立性。
② 独立したノイズ条件。
③ 最小限の (そして独立した) 変更。
因果関係系の識別可能性については、一般的に機械学習自体は、予測結果が正確か最適かを判断する必要があるなど、機械学習自体はあまり重視されていません。それは「真実」ではありません。しかし、因果分析・因果表現学習はデータの「真実」を復元すること、つまりデータの背後にある因果関係を特定できるかどうかに重点を置きます。
2 つの基本概念を以下に紹介します。
① 因果関係の発見: データを通じて根底にある因果構造/モデルを探索します。
② 因果表現学習: 直接観察されたデータから、根底にある高レベルの隠れた変数と変数間の関係を見つけます。
2. 因果表現の学習の分割
因果表現の学習方法は、一般的に次の 3 つの観点から分類されます:
① データの性質: 独立しているか、等分布しているか ( 「i.i.d.データ」)。非独立かつ同一分布のデータには、時間依存性のある同一分布のデータ(時系列データなど)や、データ分布の変化などの独立ではあるが異なる分布のデータ(あるいはこれら2つの組み合わせ)が含まれる。そのうち)。
② パラメータ制約 (「パラメータ制約」): パラメータ モデルなど、因果関係の影響に関するその他の追加プロパティがあるかどうか。
③ 潜在的交絡因子 (「潜在的交絡因子」): システム内に観察されていない共通因子または交絡因子の存在を許可するかどうか。
次の図は、さまざまな設定で得られる具体的な結果を詳細に示しています。

たとえば、独立した同一の分布の場合、パラメーター モデルがない場合、潜在的な交絡因子があるかどうかに関係なく、制約は一般に同値クラス (「同値クラス」) を取得できます。パラメトリック モデル制約がある場合は、通常、その背後にある真実を直接復元できます。
3. 独立かつ同一分布の因果表現の学習

上図は、独立かつ同一分布の状況におけるパラメータ モデル制約のない例を示しています。このデータには、性別、場所、天候、頭蓋骨のサイズと形状など、250 個の頭蓋骨に関する合計 8 つの測定変数が示されています。考古学者は、地域ごとに人々の外見が異なる原因を知りたいと考えており、この因果関係がわかれば、環境の変化などから人々の外見を予測できる可能性があります。このような状況では当然人間の介入は不可能であり、介入を加えたとしても結果を観測するまでに長時間を要するため、因果関係は既存の観測データからしか見出すことができない。

上の図に示すように、変数間の関係は非常に複雑で、線形または非線形の場合があり、変数の次元が一貫していない場合もあります。性別が 1 次元である場合、頭蓋骨の特徴は 255 次元になる可能性があります。このとき、条件付き独立性の性質を利用して因果関係を構築することができます。
手法には次の 2 種類があります。
① PC (Peter-Clark) アルゴリズム: このアルゴリズムは、システム内に共通因子が観察されないことを前提としています。
② FCI アルゴリズム: 隠れた変数がある場合に使用されます。
PC アルゴリズムは、以下の考古学的データの分析に使用されます。X3 が与えられた場合に変数 X1 と X5 が条件的に独立するなど、一連の条件付き独立プロパティをデータから導き出すことができます。同時に、2 つの変数が条件付きで独立している場合、それらの間にエッジは存在しないことを証明できます。次に、完全なグラフから開始できます。変数が条件付きで独立している場合は、接続されているエッジを削除して無向グラフを取得します。次に、グラフ内のエッジの方向を判断して、有向非巡回グラフを見つけます。(DAG、有向非巡回グラフ) Graph)、またはデータ内の変数間の条件付き独立性制約を満たす有向非巡回グラフのコレクション。

上の図は、PC アルゴリズムとカーネル条件独立性テスト法を使用して考古学データを分析した結果を示しています。地理的位置は天候に影響し、天候は頭蓋骨のサイズに影響し、性別も影響します。頭蓋骨の大きさなどに影響を与える可能性があります。その背後にある因果関係がデータ分析によって得られました。
今述べた 2 つの問題のうち、1 つは変数 DAG の各エッジの方向を見つけることであり、これには追加の仮定が必要です。原因が結果にどのように影響するかについていくつかの仮定を置くと、原因と結果が非対称であることがわかり、原因と結果の方向を知ることができます。以下の図のデータの背景は依然として独立しており、同一に分散されたデータであり、追加のパラメーター制限が追加されており、システムでは依然として交絡因子が許可されていません。このとき、因果方向の検討には次の 3 種類のモデルを使用できます:
① 線形非ガウス モデル;
② ポスト非線形因果モデル (PNL、Post -nonlinear)因果モデル);
③ 加法的ノイズ モデル (ANM、加法的ノイズ モデル)。

線形非ガウス モデルでは、X が Y につながる、つまり X が従属変数、Y が効果変数であると仮定されます。図からわかるように、線形回帰の Y を説明するために X を使用する場合、残差と X は独立していますが、逆に Y を使用して説明する場合、明らかに独立していません (線形ガウスの場合、変数間の無相関を意味します)。ただし、現時点ではモデルは線形非ガウスモデルです、つまり、相関がないことはそれらが独立していることを意味しません)。従属変数と効果変数の間に非対称性があることがわかります。同じことがポスト非線形因果モデルと加法性ノイズ モデルにも当てはまります。

上の図は、非線形後の因果モデルを示しています。外側の 2 番目の非線形関数 (f2) は、通常、測定プロセスで導入された非線形要因を記述するために使用されます。データを観察/測定する際には、線形の変化もあれば、非線形の変化が起こることもよくあります。たとえば、生物学の分野では、機器を使用して遺伝子発現データを測定するときに、追加の非線形変化が発生します。線形モデル、非線形加法ノイズ モデル、乗算ノイズ モデルはすべて PNL モデルの特殊なケースです。

上の散布図は、変数 x1 (標高) と x2 (年間降雨量) の関係を示しています。まず、x1 が x2 の原因であると仮定し、データに適合するモデルを構築します。左下隅に示すように、残差と x1 は独立しています。次に、x2 が x1 の原因であると仮定して、モデルを再度適合させます。残差が一致していることがわかります。と x2 は独立していません (中央の図を参照)。このことから、因果方向は x1 が x2 につながることによって引き起こされると結論付けられます。

確かに前述の例から因果変数の非対称性がわかるのですが、この結果は理論的に保証できるのでしょうか?そして、それが唯一の正しい結果であり、その逆方向(結果から原因)ではデータを説明できないのでしょうか?証明は上の表の通りで、データを両方向(原因から結果、結果から原因)で説明できるケースが 5 つあり、これら 5 つは非常に特殊なケースです。 1 つ目は線形ガウス モデルです。このモデルでは、関係が線形で分布がガウス分布になり、因果関係の非対称性がなくなります。残りの4台は特別モデルです。

ポスト非線形モデルを使用してデータを分析した場合でも、原因と結果を区別できます。独立した残差は正しい方向には見つかりますが、逆方向には見つかりません。方向に到着しました。線形モデルと非線形付加ノイズ モデルは両方ともポスト非線形モデルの特殊なケースであるため、両方のモデルがこのケースにも適用でき、因果関係の方向を見つけることができます。
2 つの変数が与えられた場合、それらの因果関係の方向は上記の方法で見つけることができます。例えば、心理学の分野では、いくつかの質問 (xi) に対する回答がアンケートによって収集されますが、これらの回答の間には依存関係があり、相関関係があるとは考えられません。これらの回答間の関係、直接的な因果関係。

しかし、上の図に示すように、これらの xi は、その背後にある隠し変数 Li と一緒に生成されます。隠れた変数 Li と、観測された xi を通じて隠れた変数間の関係を明らかにする方法が特に重要です。

近年、これらの従属変数とその関係を見つけるのに役立ついくつかの方法が登場しました。上図は、一連の問題を解決できる一般化独立ノイズ (GIN) 法の適用例を示しています。データの内容は教師の職業上の燃え尽き症候群であり、28 個の変数が含まれています。右の図は、これらのバーンアウト状態を引き起こす可能性のある専門家によって提案された潜在変数 (観測変数) と、潜在変数間の関係を示しています。 GIN 法による観測データの分析によって得られた結果は、専門家によって与えられた結果と一致しています。専門家は定性的な背景知識に基づいて分析を行い、データ分析の定量的な分析手法は専門家の結果の検証とサポートを提供します。

#さらに詳細な分析のために、潜在変数は階層的である、つまり、潜在変数の階層構造 (Latent Hierarchical Structure) であると仮定できます。観察された変数 xi を分析することにより、隠れた変数 Li とその背後にあるそれらの関係を明らかにすることができます。
3. 時系列から学ぶ因果表現
独立等分布状況下での因果表現法を理解したところで、次は非線形条件下での独立等分布法を使用する方法を紹介します。その背後にある隠れた変数と因果関係を見つける方法。一般に、独立した同一の分布の場合、因果関係を見つけるには比較的強い条件(パラメトリック モデルの仮定、線形モデル、疎なグラフなどを含む)が必要です。他の場合には、因果関係をより簡単に見つけることができます。


 #上の図は、より実用的な方法を示しています。ビデオ データでは、データの背後にある真に意味のある潜在的なプロセスは、私たちが観察するデータが、その反映として、可逆的な滑らかな非線形関数による変換によって生成されることです。実際の暗黙的な因果関係には、一般に「押してから落ちる」など、時間的な因果関係があり、この因果関係は一般に時間遅延します。これらの条件下では、非常に弱い仮定の下でも (基礎となる潜在プロセスがノンパラメトリックであり、g 関数 (潜在プロセスから観測時系列まで) もノンパラメトリックであっても)、基礎となる潜在プロセスを完全に理解することができます。すべてが明らかになりました。
#上の図は、より実用的な方法を示しています。ビデオ データでは、データの背後にある真に意味のある潜在的なプロセスは、私たちが観察するデータが、その反映として、可逆的な滑らかな非線形関数による変換によって生成されることです。実際の暗黙的な因果関係には、一般に「押してから落ちる」など、時間的な因果関係があり、この因果関係は一般に時間遅延します。これらの条件下では、非常に弱い仮定の下でも (基礎となる潜在プロセスがノンパラメトリックであり、g 関数 (潜在プロセスから観測時系列まで) もノンパラメトリックであっても)、基礎となる潜在プロセスを完全に理解することができます。すべてが明らかになりました。
これは、実際の暗黙的なプロセスに戻った後は、瞬間的な因果関係や依存関係がなくなり、オブジェクト間の関係がより明確になるためです。しかし、ビデオデータのピクセルを直接観察するなど、観察データを間違った分析方法で観察すると、それらの間に瞬間的な依存関係があることがわかります。
上の図は 2 つの単純なケースを示しています: 左側は KiTTiMask ビデオ データを示しています。ビデオ データを分析すると、一方向の移動、垂直方向の移動、マスク サイズの変更という 3 つの暗黙的なプロセスが得られます。右側は、色の異なる5つの小さな球を示しています。いくつかの球はバネ(目に見えません)で接続されています。解析により、10個の隠れた変数(5つの小さな球のx、y座標)が得られ、それらの間の因果関係がわかります。関係がわかります (いくつかのボールの間にはバネがあります)。ビデオデータに基づいて、完全に教師なしの方法を直接使用し、原因と結果の原理を導入して、その背後にあるオブジェクト間の関係を見つけることができます。
4. 複数の分布の下での因果表現の学習
最後に、データ分布が変化したときの因果分析を紹介します。変数/プロセスを時間の経過とともに記録すると、基礎となる未観察/測定変数の値の変化によりデータ分布が時間の経過とともに変化し、それに応じて観察変数のデータ分布が変化することがよくわかります。同様に、異なる条件でデータを測定すると、異なる条件/場所で測定されたデータの分布も異なる可能性があることがわかります。

ここで強調すべき点は、因果モデリングとデータ分布の変化との間には非常に密接な関係があるということです。モジュールの性質に基づいて因果モデルが与えられると、これらのサブモジュールは独立して変化する可能性があり、この変化をデータから観察できれば、因果モデルの正しさを検証できます。ここで言う因果モデルの変化とは、因果関係の影響が強くなったり弱くなったり、あるいは消滅したりする可能性があることを意味します。

非定常データ/異種データでは、因果関係をより直接的に発見できます。観測変数が与えられた後、次のようになります。変数の因果関係の生成プロセスは変化します;
② 因果関係の影響の無向エッジ (骨格) を決定します; 
影響それらの間の非対称性は非定常性を通じて見つけることができます。多くの場合、さまざまなセクターがクラスター内に存在し、密接に関連しています。右下隅の画像は、時間の経過に伴う株価変動の因果過程を示しており、2 つの縦軸はそれぞれ 2007 年と 2008 年の金融危機を表しています。
 多分布条件下での因果分析手法により、さまざまなデータセットからデータの変化パターンを見つけることができ、直接適用して転移学習や学習を実行できます。ドメイン適応です)。上の図に示すように、さまざまなデータセットからデータの変化する規則を見つけ出し、拡張グラフを使用してデータの分布がどのように変化するかを示すことができます。図の theta_Y は、Y がそれに与えている分布を表します。親ノードはそのドメインに応じて変更できます。データ分布の変化を表すグラフに基づいて、新しいフィールドまたは対象フィールドの Y を予測するという非常に標準的な問題、つまり、特徴量が与えられた場合に Y の事後確率をどのように求めるかという推論問題です。
多分布条件下での因果分析手法により、さまざまなデータセットからデータの変化パターンを見つけることができ、直接適用して転移学習や学習を実行できます。ドメイン適応です)。上の図に示すように、さまざまなデータセットからデータの変化する規則を見つけ出し、拡張グラフを使用してデータの分布がどのように変化するかを示すことができます。図の theta_Y は、Y がそれに与えている分布を表します。親ノードはそのドメインに応じて変更できます。データ分布の変化を表すグラフに基づいて、新しいフィールドまたは対象フィールドの Y を予測するという非常に標準的な問題、つまり、特徴量が与えられた場合に Y の事後確率をどのように求めるかという推論問題です。
 上の図は、シミュレーション データと実際のデータに対する因果表現法の推論効果の精度が大幅に向上していることを示しています。質的変化のルールと異なる分野の変動の大きさに基づいて、新しい分野が出現したときに適応的な調整が行われるため、この種の予測効果はより高くなります。
上の図は、シミュレーション データと実際のデータに対する因果表現法の推論効果の精度が大幅に向上していることを示しています。質的変化のルールと異なる分野の変動の大きさに基づいて、新しい分野が出現したときに適応的な調整が行われるため、この種の予測効果はより高くなります。
上の図は、ドメイン適応のための部分的もつれ解除に関連する最近の研究を示しています。特徴とターゲットを考慮して、すべてがノンパラメトリックであり、一部の要因はドメインによって変化しないと仮定します。つまり、分布は安定していますが、一部の要因は変化する可能性があります。分布を変化させるこれらのごく少数の要因を見つけることを期待します。見つかった要因に基づいて、異なる分野を調整し、異なる分野間の対応関係を見つけることができるため、ドメイン適応/転移学習は当然のことになります。分布の変化の背後にある独立した要因は観測データから直接復元でき、変化していない要因はその部分空間を復元できることが証明できます。表に示すように、上記の方法はドメイン適応において良好な結果を達成できます。同時に、この方法は最小変化の原則にも準拠しています。つまり、最も変化の少ない要素を使用して、異なるフィールドのデータの要素がどのように変化したかを説明し、それらに対応させることが期待されています。

要約すると、この共有には主に次の内容が含まれます:
① 一連の機械学習の問題には、データの背後にある適切な表現が必要です。たとえば、意思決定を行う場合は、最適な意思決定を行うためにその決定の影響を知りたい場合や、ドメイン適応/一般化では、データの分布がどのように変化したかを知りたい場合があります。最適な予測、強化学習ではエージェント 環境との相互作用とその相互作用自体によってもたらされる報酬は因果関係の問題、推奨システムもユーザーが変化するため因果関係の問題、信頼できる AI、説明可能な AI、公平性はすべて因果表現に関連しています。
② 隠れた変数を含む因果関係は、特定の条件下でデータから完全に復元できます。データを通じてその背後にあるプロセスの性質を実際に理解して、それを使用することができます。
③ 原因と結果の関係は不思議ではありません。データがあり、仮説が適切であれば、その背後にある因果関係を見つけることができます。ここで行われた仮定は、テスト可能であることが望ましいです。
一般に、因果表現学習には大きな応用の可能性が秘められていますが、同時に、早急に開発する必要があり、全員の協力が必要な手法も数多くあります。
以上がCMU Zhang Kun: 因果表現テクノロジーの最新の進歩の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 踊りましょう:私たちの人間のニューラルネットを微調整するための構造化された動きApr 27, 2025 am 11:09 AM
踊りましょう:私たちの人間のニューラルネットを微調整するための構造化された動きApr 27, 2025 am 11:09 AM科学者は、彼らの機能を理解するために、人間とより単純なニューラルネットワーク(C. elegansのものと同様)を広く研究してきました。 ただし、重要な疑問が生じます。新しいAIと一緒に効果的に作業するために独自のニューラルネットワークをどのように適応させるのか
 新しいGoogleリークは、Gemini AIのサブスクリプションの変更を明らかにしますApr 27, 2025 am 11:08 AM
新しいGoogleリークは、Gemini AIのサブスクリプションの変更を明らかにしますApr 27, 2025 am 11:08 AMGoogleのGemini Advanced:Horizonの新しいサブスクリプションティア 現在、Gemini Advancedにアクセスするには、1か月あたり19.99ドルのGoogle One AIプレミアムプランが必要です。 ただし、Android Authorityのレポートは、今後の変更を示唆しています。 最新のGoogle p
 データ分析の加速がAIの隠されたボトルネックをどのように解決しているかApr 27, 2025 am 11:07 AM
データ分析の加速がAIの隠されたボトルネックをどのように解決しているかApr 27, 2025 am 11:07 AM高度なAI機能を取り巻く誇大宣伝にもかかわらず、エンタープライズAIの展開内に大きな課題が潜んでいます:データ処理ボトルネック。 CEOがAIの進歩を祝う間、エンジニアはクエリの遅い時間、過負荷のパイプライン、
 MarkitDown MCPは、任意のドキュメントをマークダウンに変換できます!Apr 27, 2025 am 09:47 AM
MarkitDown MCPは、任意のドキュメントをマークダウンに変換できます!Apr 27, 2025 am 09:47 AMドキュメントの取り扱いは、AIプロジェクトでファイルを開くだけでなく、カオスを明確に変えることです。 PDF、PowerPoint、Wordなどのドキュメントは、あらゆる形状とサイズでワークフローをフラッシュします。構造化された取得
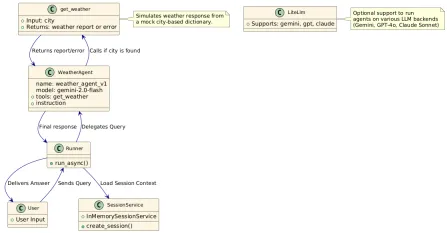 建物のエージェントにGoogle ADKを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:42 AM
建物のエージェントにGoogle ADKを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:42 AMGoogleのエージェント開発キット(ADK)のパワーを活用して、実際の機能を備えたインテリジェントエージェントを作成します。このチュートリアルは、ADKを使用して会話エージェントを構築し、GeminiやGPTなどのさまざまな言語モデルをサポートすることをガイドします。 w
 効果的な問題解決のためにLLMを介したSLMの使用 - 分析VidhyaApr 27, 2025 am 09:27 AM
効果的な問題解決のためにLLMを介したSLMの使用 - 分析VidhyaApr 27, 2025 am 09:27 AMまとめ: Small Language Model(SLM)は、効率のために設計されています。それらは、リソース不足、リアルタイム、プライバシーに敏感な環境の大手言語モデル(LLM)よりも優れています。 特にドメインの特異性、制御可能性、解釈可能性が一般的な知識や創造性よりも重要である場合、フォーカスベースのタスクに最適です。 SLMはLLMSの代替品ではありませんが、精度、速度、費用対効果が重要な場合に理想的です。 テクノロジーは、より少ないリソースでより多くを達成するのに役立ちます。それは常にドライバーではなく、プロモーターでした。蒸気エンジンの時代からインターネットバブル時代まで、テクノロジーの力は、問題の解決に役立つ範囲にあります。人工知能(AI)および最近では生成AIも例外ではありません
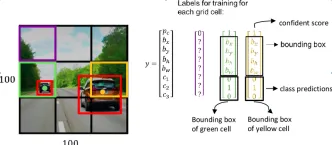 コンピュータービジョンタスクにGoogle Geminiモデルを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:26 AM
コンピュータービジョンタスクにGoogle Geminiモデルを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:26 AMコンピュータービジョンのためのGoogleGeminiの力を活用:包括的なガイド 大手AIチャットボットであるGoogle Geminiは、その機能を会話を超えて拡張して、強力なコンピュータービジョン機能を網羅しています。 このガイドの利用方法については、
 Gemini 2.0 Flash vs O4-Mini:GoogleはOpenaiよりもうまくやることができますか?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs O4-Mini:GoogleはOpenaiよりもうまくやることができますか?Apr 27, 2025 am 09:20 AM2025年のAIランドスケープは、GoogleのGemini 2.0 FlashとOpenaiのO4-Miniの到着とともに感動的です。 数週間離れたこれらの最先端のモデルは、同等の高度な機能と印象的なベンチマークスコアを誇っています。この詳細な比較


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

VSCode Windows 64 ビットのダウンロード
Microsoft によって発売された無料で強力な IDE エディター

SublimeText3 Linux 新バージョン
SublimeText3 Linux 最新バージョン

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

mPDF
mPDF は、UTF-8 でエンコードされた HTML から PDF ファイルを生成できる PHP ライブラリです。オリジナルの作者である Ian Back は、Web サイトから「オンザフライ」で PDF ファイルを出力し、さまざまな言語を処理するために mPDF を作成しました。 HTML2FPDF などのオリジナルのスクリプトよりも遅く、Unicode フォントを使用すると生成されるファイルが大きくなりますが、CSS スタイルなどをサポートし、多くの機能強化が施されています。 RTL (アラビア語とヘブライ語) や CJK (中国語、日本語、韓国語) を含むほぼすべての言語をサポートします。ネストされたブロックレベル要素 (P、DIV など) をサポートします。

ホットトピック
 7752
7752 15
15 1643
1643 14
14 1398
1398 52
52 1293
1293 25
25 1234
1234 29
29



