Java における二項対立の基本的な考え方と実装を簡単に理解する

この記事では、java に関する関連知識を提供します。二分法は非常に効率的なアルゴリズムであり、コンピューターの検索プロセスでよく使用されます。以下では、二項対立の基本的な考え方と実装について、例を挙げて詳しく説明しますので、皆様の参考になれば幸いです。

推奨学習: 「java ビデオ チュートリアル 」

順序付けされた配列で、特定の数値が存在するかどうかを確認します

アイデア:

• これは順序付けされた配列であるため、最初に中点の位置を取得でき、中点によって配列を左半分と右半分に分割できます。
• 中点位置の値が目標値と等しい場合は、中点位置を直接返します。
• 中点位置の値が目標値より小さい場合は、配列の中点の左側に移動して同様に検索します。
• 中点位置の値が目標値より大きい場合は、配列の中点の右側を取って同様に検索します。
• 最後に見つからなかった場合は、-1 を返します。

コード

class Solution {
    public int search(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
                return m;
            } else if (arr[m] > t) {
                r = m - 1;
            } else {
                l = m + 1;
            }
        }
        return -1;
    }
}

時間計算量O(logN)。

順序付けされた配列で、特定の数値以上の左端の位置を検索します。

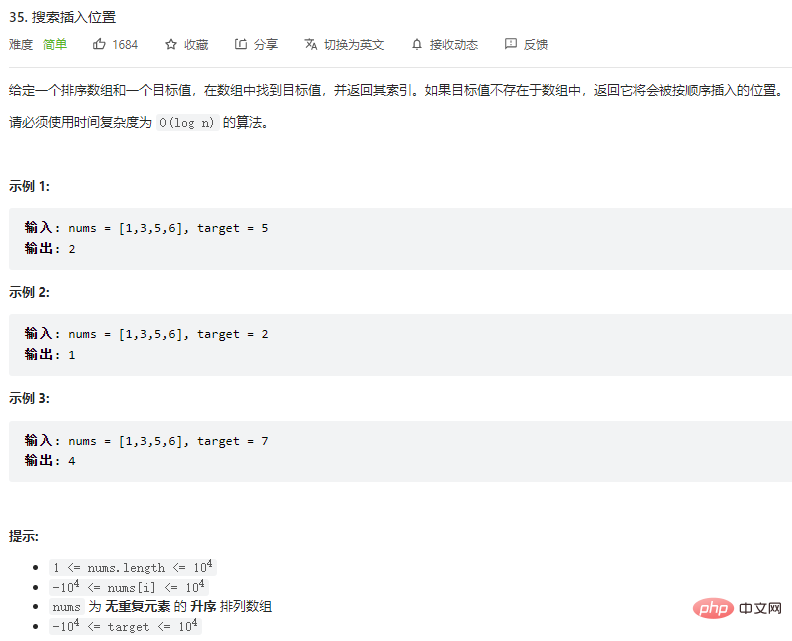
例 1:

入力: nums = [1,3,5,6], target = 5

出力: 2

説明: 配列 num## に要素 5 を挿入したい場合#、要素 3 と要素 5 の間、つまり位置 2 に挿入する必要があります。

例 2:

入力: nums = [1,3,5,6]、ターゲット = 2

出力: 1

説明:配列

num に要素 2 を挿入するには、要素 1 と要素 3 の間の位置、つまり位置 1 に要素 2 を挿入する必要があります。

例 3:

入力: nums = [1,3,5,6]、ターゲット = 7

出力: 4

説明:要素 7 を配列

num に挿入するには、要素 7 を配列の最後、つまり位置 4 に挿入する必要があります。

上記の例からわかるように、この質問は本質的に「順序付き配列で、特定の数値以上の左端の位置を見つけてください。それが存在しない場合は、戻り値を返します」というものです。配列の長さ (終了位置に挿入を表す)

上記の例に基づいて簡単な変更を加えるだけで済みます。上記の例で、条件を満たす位置が見つかった場合、直接

return

<pre class="brush:java;">if (arr[m] == t) { return m; }</pre> この質問では、

が等しい場合に左端の位置を見つける必要があるため、直接返さずに最初に位置を記録するだけで済みます。さらに左側を探索していきます。さらに左側に条件を満たす位置はありますか？

同時に、

arr[m] > t

に遭遇したときは、この時点での m の位置も記録する必要があります。も条件を満たす場所である可能性があります。 コード:

class Solution {
    public static int searchInsert(int[] arr, int t) {
        int ans = arr.length;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l)>>1);
            if (arr[m] >= t) {
                ans = m;
                r = m - 1;
            } else  {
                l = m + 1;
            } 
        }
        return ans;
    }
}

アルゴリズム全体の時間計算量は

O(logN)

です。 ソートされた配列内の要素の最初と最後の位置を見つける

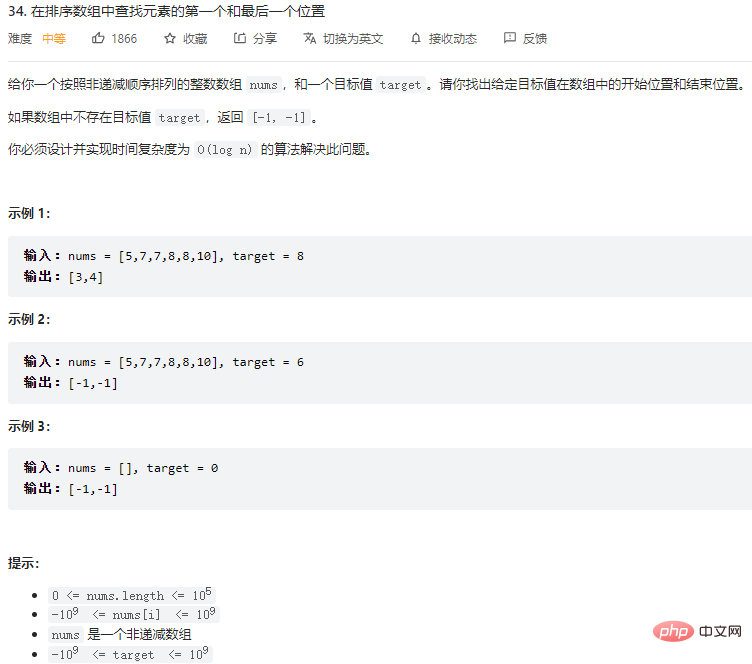アイデア

この問題も、2 進除算を使用して解決されます。 2 進除算で要素が見つかった場合は、急いで戻るのではなく、左 (右) に検索を続けて、さらに左 (右) に一致する値が見つかるかどうかを確認します。

コードは次のとおりです:

class Solution {
    public static int[] searchRange(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return new int[]{-1, -1};
        }
        return new int[]{left(arr,t),right(arr,t)};   
    }
    public static int left(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int ans = -1;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
               ans = m;
               r = m - 1;
            } else if (arr[m] < t) {
                l = m +1;
            } else {
                // arr[m] > t
                r = m - 1;
            }
        }
        return ans;
    }
    public static int right(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int ans = -1;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
               ans = m;
               l = m + 1;
            } else if (arr[m] < t) {
                l = m +1;
            } else {
                // arr[m] > t
                r = m - 1;
            }
        }
        return ans;
    }
}

時間計算量

O(logN)

。 極大問題

アイデア

配列の長さが

N

であると仮定し、最初に # を決定します。 ##0 位置の番号と N-1 位置の番号はピーク位置ですか? 0

位置は

1 位置と比較するだけで済みます。0 位置が大きい場合、0 位置 ピーク位置であり、直接戻すことができます。 N-1

位置と

N-2 位置を比較するだけで済みます。N-1 位置の方が大きい場合は、 位置 N-1 はピーク位置であり、直接返すことができます。 0

位置と

N-1 が両方とも最後の比較ラウンドの最小値である場合、配列は次のようになります。

上の図からわかるように、[0..1]

間隔は増加傾向、

[N-2.. .N-1] レンジ内では下降トレンドです。 この場合、ピーク位置は [1...N-2]

の間にある必要があります。

このとき、二分

でピーク位置を求めることができます。まず中点位置に移動し、中点位置の値が

mid であると仮定します。 Duda:

arr[mid] > arr[mid+1] && arr[mid] > arr[mid-1]

の場合、mid

位置がピーク位置となり、直接戻ります。

それ以外の場合は、次の 2 つの状況が考えられます。

ケース 1: 中間位置の値が中間 - 1 位置の値より小さい

趋势如下图：

则在[1...(mid-1)]区间内继续二分。

情况二：mid 位置的值比 mid + 1 位置的值小

趋势是：

则在[(mid+1)...(N-2)]区间内继续上述二分。

完整代码

public class LeetCode_0162_FindPeakElement {
    public static int findPeakElement(int[] nums) {
        if (nums.length == 1) {
            return 0;
        }
        int l = 0;
        int r = nums.length - 1;
        if (nums[l] > nums[l + 1]) {
            return l;
        }
        if (nums[r] > nums[r - 1]) {
            return r;
        }
        l = l + 1;
        r = r - 1;
        while (l <= r) {
            int mid = l + ((r - l) >> 1);
            if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
                return mid;
            }
            if (nums[mid] < nums[mid + 1]) {
                l = mid + 1;
            } else if (nums[mid] < nums[mid - 1]) {
                r = mid - 1;
            }
        }
        return -1;
    }
}

时间复杂度O(logN)。

推荐学习：《java视频教程》

以上がJava における二項対立の基本的な考え方と実装を簡単に理解するの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。