ホームページ >Java >&#&チュートリアル >Javaのデータ構造とアルゴリズムの詳細な図解説明
Javaのデータ構造とアルゴリズムの詳細な図解説明
- WBOY転載
- 2022-03-21 17:35:112415ブラウズ
この記事では、java に関する関連知識を提供し、主に Java コードの実装、アノテーション分析、アルゴリズム分析などを紹介します。画像とテキストによる詳細な説明が皆様のお役に立てれば幸いです。

java 学習チュートリアル 」
第 1 章 データ構造とアルゴリズムの基礎の概要 1.1データ構造とアルゴリズムの重要性- ##アルゴリズムはプログラムの魂 優れたプログラムは、大量のデータを計算しても高速な計算を維持できます
- #データ構造とアルゴリズムの関係
:
プログラム = データ構造アルゴリズム- データ構造は、アルゴリズム、言い換えれば、アルゴリズムをよく学びたければ、データ構造をよく知る必要があります。
#データ構造とアルゴリズム学習の概要 -
1.2 データ構造の概要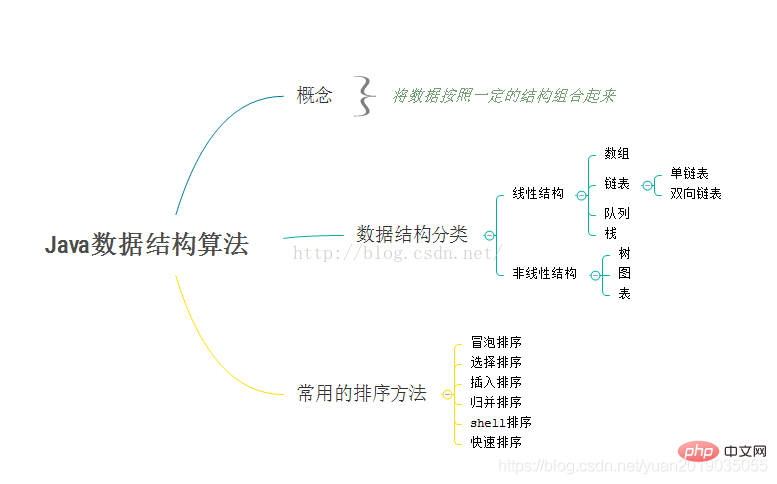
データ構造は、データ間の関係として簡単に理解でき、データの記憶構造とデータの論理構造に分けられます。
論理構造
- : データ要素は同じセットに属し、並列されます。関係性、それ以外の関係性はありません。中学校の学習の集合体として理解できます。範囲内には多くの要素があり、要素間に関係性はありません。
- 線形構造 : 要素間は 1 対 1 の関係にあり、各生徒に生徒番号が対応しており、生徒番号と名前が線形構造になっていることが分かります
- ツリー構造 :要素間には一対の関係があります。多数の関係は、世代を超えた家族の系図として簡単に理解できます。
- グラフィック構造 : 要素間には多対多の関係があります。各要素は複数の要素に対応する場合があります。または、複数の要素に対応する、ネットワーク グラフ
- ストレージ構造
- : という意味です。データを継続的に保存することで、学校のカフェテリアで次々と食事の列に並ぶのと比較できます。
- 連鎖ストレージ構造 : 順序どおりに保存されるわけではありません。次に来る番号は次のとおりです。 in はアドレスを伝えるだけで済みます。前のノードには、その後ろの番号のアドレスが格納されているため、最後の番号の格納アドレスは null になります。この構造は、ショッピング モールで電話をかけるのと比較できます。後続のアドレスは何ですか? 上の他の内容はノードの内容です;
- 違い :
-
Theシーケンシャル ストレージの特徴は、クエリが速く、挿入または削除が遅いことです。
- チェーン ストレージの特徴は、クエリが遅く、挿入または削除が速いことです。
同じ問題をさまざまな方法で解決します。方法
- 時間と空間の複雑さによってアルゴリズムの品質を判断します。
- 最良のアルゴリズムはありません。学習アルゴリズムは、学習アイデアを蓄積し、学習アイデアを習得するものであり、特定の問題を解決して特定のアルゴリズムを記憶するものではありません。時間計算量と空間計算量に関しては、現在のほとんどの開発状況では、時間のために空間を使用しており、消費しています。より高速な速度を確保するには、より多くのメモリを使用します。
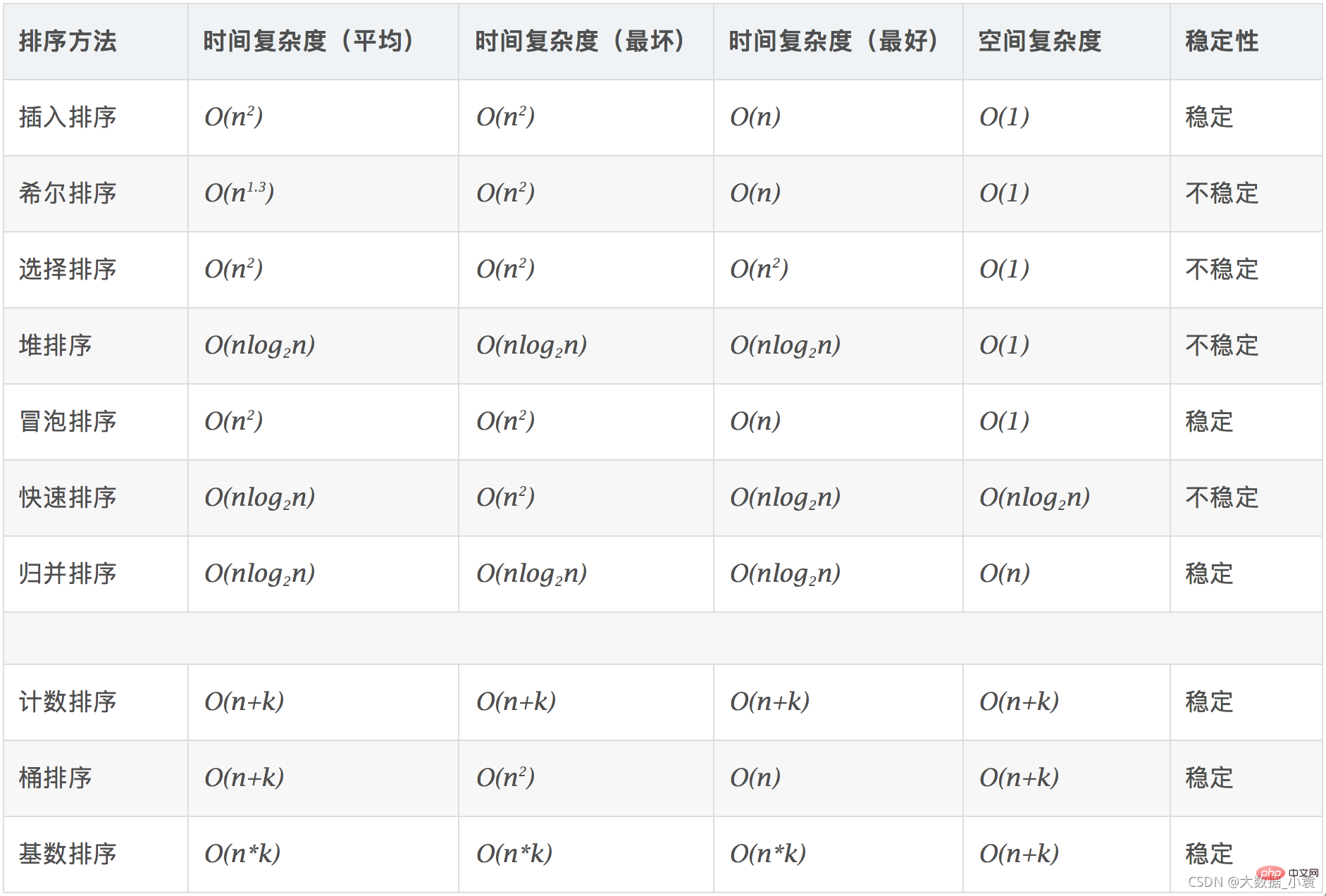
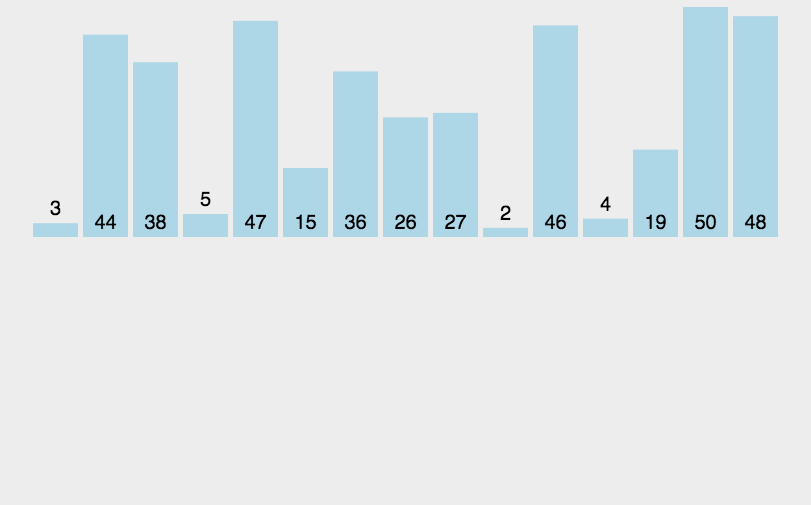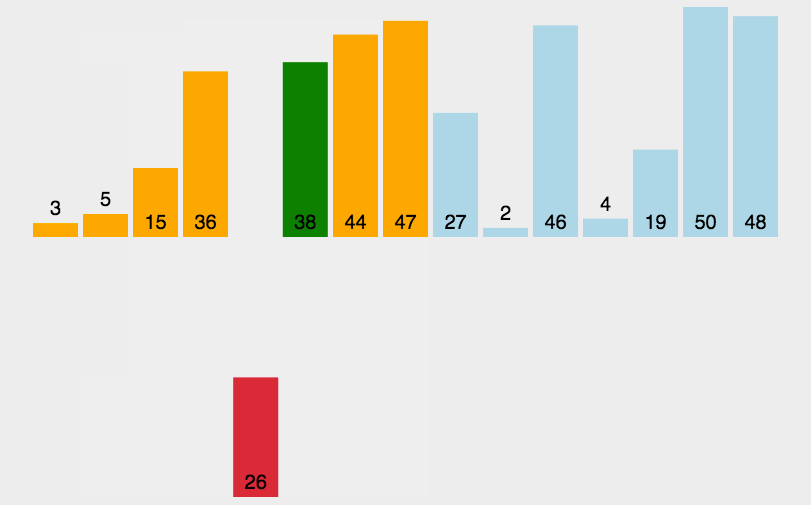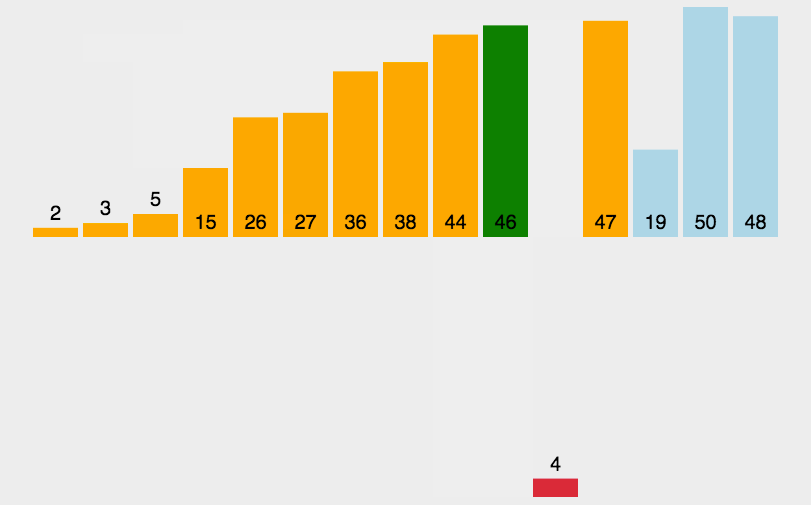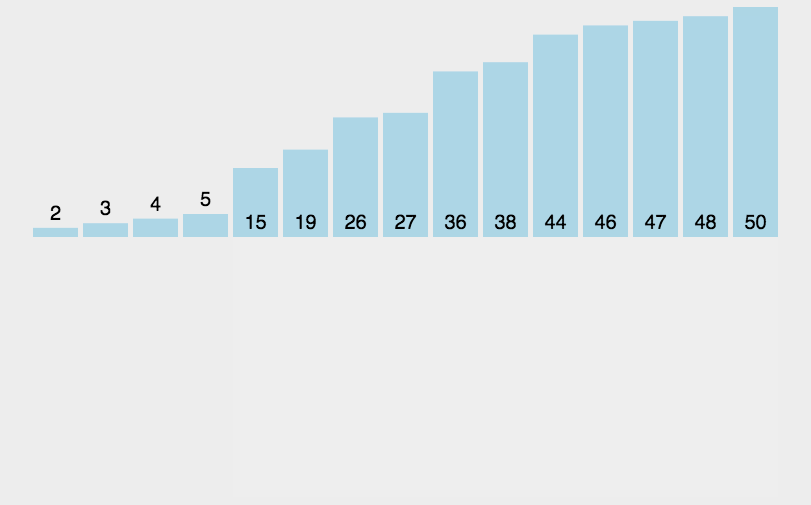
- 各ソートアルゴリズムの複雑さと安定性 :
-
 「ビッグオー記法」の理解方法
「ビッグオー記法」の理解方法
T(n)
として記録されます。 n は問題のスケールと呼ばれ、n が変化し続けると、時間周波数T(n) も変化し続けます。しかし、場合によっては、変化したときにどのようなパターンが示されるかを知りたいことがあります。この目的を達成するために、Time Complexity の概念を導入します。
一般に、アルゴリズムの基本操作が繰り返される回数は、問題サイズ n の関数であり、T(n) で表されます。補助関数がある場合は、f( n) 、n が無限大に近づくと、T(n)/f(n) の限界値はゼロに等しくない定数となり、f( n) は、T(n) と同じ桁の大きさの関数 です。 T(n)=O(f(n)) として表される、O(f(n)) をアルゴリズムの 漸近時間計算量 と呼びます。 時間計算量と略されます。
時間計算量の基本的な計算規則:
- 基本的な演算、つまり定数項のみの時間計算量は O(1) であると見なされます。
- シーケンシャル構造、時間計算量は
- 加算に従って計算されます ループ構造、時間計算量は
- 乗算に従って計算されます 分岐構造、時間 複雑さ
- 最大値をとる アルゴリズムの効率を判断するとき、多くの場合、演算数の最上位の項に注目するだけで十分です。および定数項は無視できます。
- 特に指定がない限り、分析するアルゴリズムの時間計算量は、
- 最悪の時間計算量
一般的な時間計算量を指します。 :
- 注
: Log2n (底 2 の対数) は、logn
:
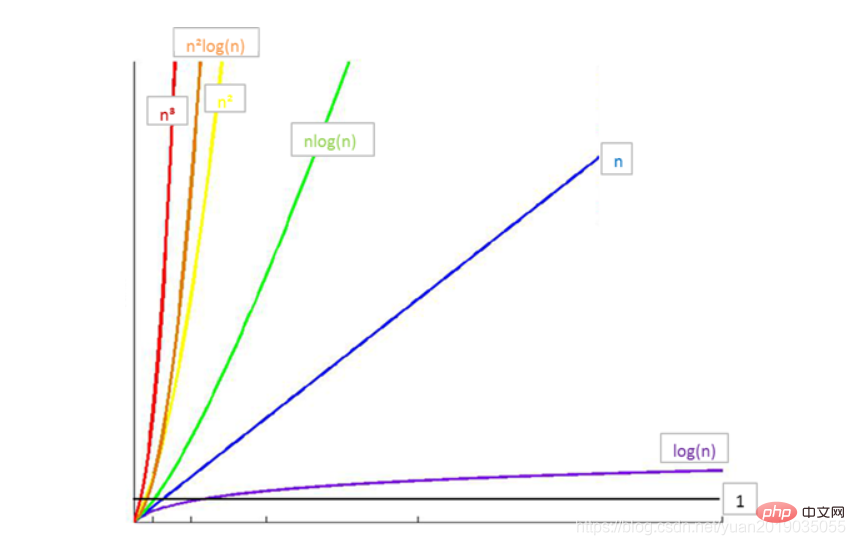
- つまり、小規模から大規模までの時間消費量は
- :O( 1 )
: count = 0; (1)
for(i = 0;i
- ステートメント (2) を実行します。
- ステートメントを n 回実行します (3)
- ステートメントを n^2 回実行します (4)
- ステートメントを n^2 回実行します。は
- : T(n) = 1 n n^2 n^2 = O(n^2)
a = 1; (1) b = 2; (2) for(int i = 1;i <strong> </strong> ステートメント (1)、(2) は 1 回実行されます
- ステートメント (3) は n 回実行されます
- ステートメント (4)、(5)、(6)は n 回実行されます
- 時間計算量は :
- T(n) = 1 1 4n = o(n)
i = 1; (1)while(i<n i><strong></strong>ステートメント (1) の頻度は 1<ul>ステートメント (2) の頻度は <li>f(n)## であるとします。 #、次に </li>2f(n)、最大値を取る <code>f(n) = log2n</code><code></code><code>時間計算量は </code>:T(n) = O(log2n)<li>
<strong></strong><code>空間計算量</code>
</li>
</ul>
<h3>空間アルゴリズムの複雑さの計算式: </h3>S(n) = 0( f(n) )<ul>、n は入力サイズ、<li>f(n)<p> は記憶域の関数です。ステートメント内の n によって占有される<code></code><code></code>コンピューター メモリ上でアルゴリズムによって占有される記憶域には 3 つの側面があります</p>
</li>#記憶域アルゴリズム自体によって占有される記憶域<li>
<p>アルゴリズムの入力 出力データが占有する記憶領域 </p>
<ul>#操作中にアルゴリズムが一時的に占有する記憶領域 <li>
<li>
<li>Case</ul>: 指定された配列が使用されます。 Reverse して、反転した内容を返します。</li>
</ul>解決策 1:<p></p>
<pre class="brush:php;toolbar:false">public static int[] reverse1(int[] arr) {
int n = arr.length; //申请4个字节
int temp; //申请4个字节
for (int start = 0, end = n - 1; start <strong></strong>空間の複雑さは <p>:## です。 #S(n) = 4 4 = O(8) = O(1)</p>
-
解決策 2:
public static int[] reverse2(int[] arr) { int n = arr.length; //申请4个字节 int[] temp = new int[n]; //申请n*4个字节+数组自身头信息开销24个字节 for (int i = n - 1; i >= 0; i--) { temp[n - 1 - i] = arr[i]; } return temp;}空間の複雑さは次のとおりです。
S( n) = 4 4n 24 = O(n 28) = O(n)
-
ビッグ O 導出ルールによると、次の空間複雑さは次のようになります。アルゴリズム 1 は 0(1)、アルゴリズム 2 の空間複雑度は 0(n) であるため、空間占有の観点からは、アルゴリズム 1 の方がアルゴリズム 2 よりも優れています。
Java にはメモリ ガベージ コレクション メカニズムがあり、JVM はプログラムのメモリ使用量 (ジャストインタイム コンパイルなど) も最適化するため、Java プログラムのメモリ使用量を正確に評価することはできません。 、しかし、Java の基本的なメモリを理解しています。占有により、Java プログラムのメモリ使用量を推定できるようになります。現在のコンピュータ機器のメモリは一般的に比較的大きいため、基本的にパーソナル コンピュータは 4G から始まり、より大きなものでは 32G に達する可能性があるため、メモリ使用量は通常、アルゴリズムのボトルネックにはなりません。複雑さについて直接話しましょう。デフォルトはアルゴリズムの時間計算量です。
第2章 数组
2.1 数组概念
数组是一种线性表数据结构,它用一组连续的内存空间,来存储一组具有相同类型的数据。这里我们要抽取出三个跟数组相关的关键词:线性表,连续内存空间,相同数据类型;数组具有连续的内存空间,存储相同类型的数据,正是该特性使得数组具有一个特性:随机访问。但是有利有弊,这个特性虽然使得访问数组边得非常容易,但是也使得数组插入和删除操作会变得很低效,插入和删除数据后为了保证连续性,要做很多数据搬迁工作。
查找数组中的方法有两种:
- 线性查找:线性查找就是简单的查找数组中的元素
- 二分法查找:二分法查找要求目标数组必须是有序的。
2.2 无序数组
- 实现类:
public class MyArray {
//声明一个数组
private long[] arr;
//有效数据的长度
private int elements;
//无参构造函数,默认长度为50
public MyArray(){
arr = new long[50];
}
public MyArray(int maxsize){
arr = new long[maxsize];
}
//添加数据
public void insert(long value){
arr[elements] = value;
elements++;
}
//显示数据
public void display(){
System.out.print("[");
for(int i = 0;i = elements || index = elements || index = elements || index
-
优点:插入快(时间复杂度为:
O(1))、如果知道下标,可以很快存储 -
缺点:查询慢(时间复杂度为:
O(n))、删除慢
2.3 有序数组
- 实现类:
public class MyOrderArray {
private long[] arr;
private int elements;
public MyOrderArray(){
arr = new long[50];
}
public MyOrderArray(int maxsize){
arr = new long[maxsize];
}
//添加数据
public void insert(int value){
int i;
for(i = 0;i value){
break;
}
}
for(int j = elements;j > i;j--){
arr[j] = arr[j -1];
}
arr[i] = value;
elements++;
}
//删除数据
public void delete(int index){
if(index >=elements || index = elements || index = elements || index pow){
return -1;
}else{
if(arr[middle] > value){
//待查询的数在左边,右指针重新改变指向
pow = middle-1;
}else{
//带查询的数在右边,左指针重新改变指向
low = middle +1;
}
}
}
}}
-
优点:查询快(时间复杂度为:
O(logn)) -
缺点:增删慢(时间复杂度为:
O(n))
第三章 栈
3.1 栈概念
栈(stack),有些地方称为堆栈,是一种容器,可存入数据元素、访问元素、删除元素,它的特点在于只能允许在容器的一端(称为栈顶端指标,英语:top)进行加入数据(英语:push)和输出数据(英语:pop)的运算。没有了位置概念,保证任何时候可以访问、删除的元素都是此前最后存入的那个元素,确定了一种默认的访问顺序。
由于栈数据结构只允许在一端进行操作,因而按照后进先出的原理运作。
栈可以用顺序表实现,也可以用链表实现。

3.2 栈的操作
- Stack() 创建一个新的空栈
- push(element) 添加一个新的元素element到栈顶
- pop() 取出栈顶元素
- peek() 返回栈顶元素
- is_empty() 判断栈是否为空
- size() 返回栈的元素个数
实现类:
package mystack;public class MyStack {
//栈的底层使用数组来存储数据
//private int[] elements;
int[] elements; //测试时使用
public MyStack() {
elements = new int[0];
}
//添加元素
public void push(int element) {
//创建一个新的数组
int[] newArr = new int[elements.length + 1];
//把原数组中的元素复制到新数组中
for (int i = 0; i <p><strong>测试类</strong>:</p><pre class="brush:php;toolbar:false">package mystack;public class Demo {
public static void main(String[] args) {
MyStack ms = new MyStack();
//添加元素
ms.push(9);
ms.push(8);
ms.push(7);
//取出栈顶元素// System.out.println(ms.pop()); //7// System.out.println(ms.pop()); //8// System.out.println(ms.pop()); //9
//查看栈顶元素
System.out.println(ms.peek()); //7
System.out.println(ms.peek()); //7
//查看栈中元素个数
System.out.println(ms.size()); //3
}}第4章 队列
4.1 队列概念
队列(Queue)是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。
队列是一种先进先出的(First In First Out)的线性表,简称FIFO。允许插入的一端为队尾,允许删除的一端为队头。队列不允许在中间部位进行操作!假设队列是q=(a1,a2,……,an),那么a1就是队头元素,而an是队尾元素。这样我们就可以删除时,总是从a1开始,而插入时,总是在队列最后。这也比较符合我们通常生活中的习惯,排在第一个的优先出列,最后来的当然排在队伍最后。
同栈一样,队列也可以用顺序表或者链表实现。

4.2 队列的操作
- Queue() 创建一个空的队列
- enqueue(element) 往队列中添加一个element元素
- dequeue() 从队列头部删除一个元素
- is_empty() 判断一个队列是否为空
- size() 返回队列的大小
实现类:
public class MyQueue {
int[] elements;
public MyQueue() {
elements = new int[0];
}
//入队
public void enqueue(int element) {
//创建一个新的数组
int[] newArr = new int[elements.length + 1];
//把原数组中的元素复制到新数组中
for (int i = 0; i <p><strong>测试类</strong>:</p><pre class="brush:php;toolbar:false">public class Demo {
public static void main(String[] args) {
MyQueue mq = new MyQueue();
//入队
mq.enqueue(1);
mq.enqueue(2);
mq.enqueue(3);
//出队
System.out.println(mq.dequeue()); //1
System.out.println(mq.dequeue()); //2
System.out.println(mq.dequeue()); //3
}}第5章 链表
5.1 单链表
单链表概念
单链表也叫单向链表,是链表中最简单的一种形式,它的每个节点包含两个域,一个信息域(元素域)和一个链接域。这个链接指向链表中的下一个节点,而最后一个节点的链接域则指向一个空值。

- 表元素域data用来存放具体的数据。
- 链接域next用来存放下一个节点的位置
单链表操作
- is_empty() 链表是否为空
- length() 链表长度
- travel() 遍历整个链表
- add(item) 链表头部添加元素
- append(item) 链表尾部添加元素
- insert(pos, item) 指定位置添加元素
- remove(item) 删除节点
- search(item) 查找节点是否存在
实现类:
//一个节点public class Node {
//节点内容
int data;
//下一个节点
Node next;
public Node(int data) {
this.data = data;
}
//为节点追加节点
public Node append(Node node) {
//当前节点
Node currentNode = this;
//循环向后找
while (true) {
//取出下一个节点
Node nextNode = currentNode.next();
//如果下一个节点为null,当前节点已经是最后一个节点
if (nextNode == null) {
break;
}
//赋给当前节点,无线向后找
currentNode = nextNode;
}
//把需要追加的节点,追加为找到的当前节点(最后一个节点)的下一个节点
currentNode.next = node;
return this;
}
//显示所有节点信息
public void show() {
Node currentNode = this;
while (true) {
System.out.print(currentNode.data + " ");
//取出下一个节点
currentNode = currentNode.next;
//如果是最后一个节点
if (currentNode == null) {
break;
}
}
System.out.println();
}
//插入一个节点作为当前节点的下一个节点
public void after(Node node) {
//取出下一个节点,作为下下一个节点
Node nextNext = next;
//把新节点作为当前节点的下一个节点
this.next = node;
//把下下一个节点设置为新节点的下一个节点
node.next = nextNext;
}
//删除下一个节点
public void removeNode() {
//取出下下一个节点
Node newNext = next.next;
//把下下一个节点设置为当前节点的下一个节点
this.next = newNext;
}
//获取下一个节点
public Node next() {
return this.next;
}
//获取节点中的数据
public int getData() {
return this.data;
}
//判断节点是否为最后一个节点
public boolean isLast() {
return next == null;
}}
测试类:
public class Demo {
public static void main(String[] args) {
//创建节点
Node n1 = new Node(1);
Node n2 = new Node(2);
Node n3 = new Node(3);
//追加节点
n1.append(n2).append(n3);
//取出下一个节点数据
System.out.println(n1.next().next().getData()); //3
//判断节点是否为最后一个节点
System.out.println(n1.isLast()); //false
System.out.println(n1.next().next().isLast()); //true
//显示所有节点信息
n1.show(); //1 2 3
//删除一个节点// n1.next.removeNode();// n1.show(); //1 2
//插入一个新节点
n1.next.after(new Node(0));
n1.show(); //1 2 0 3
}}
5.2 循环链表
循环链表概念
单链表的一个变形是单向循环链表,链表中最后一个节点的 next 域不再为 None,而是指向链表的头节点。
循环链表操作
实现类:
//表示一个节点public class LoopNode {
//节点内容
int data;
//下一个节点
LoopNode next = this; //与单链表的区别,追加了一个this,当只有一个节点时指向自己
public LoopNode(int data) {
this.data = data;
}
//插入一个节点
public void after(LoopNode node) {
LoopNode afterNode = this.next;
this.next = node;
node.next = afterNode;
}
//删除一个节点
public void removeNext() {
LoopNode newNode = this.next.next;
this.next = newNode;
}
//获取下一个节点
public LoopNode next() {
return this.next;
}
//获取节点中的数据
public int getData() {
return this.data;
}}
测试类:
public class Demo {
public static void main(String[] args) {
//创建节点
LoopNode n1 = new LoopNode(1);
LoopNode n2 = new LoopNode(2);
LoopNode n3 = new LoopNode(3);
LoopNode n4 = new LoopNode(4);
//增加节点
n1.after(n2);
n2.after(n3);
n3.after(n4);
System.out.println(n1.next().getData()); //2
System.out.println(n2.next().getData()); //3
System.out.println(n3.next().getData()); //4
System.out.println(n4.next().getData()); //1
}}
5.3 双向循环链表
双向循环链表概念
在双向链表中有两个指针域,一个是指向前驱结点的prev,一个是指向后继结点的next指针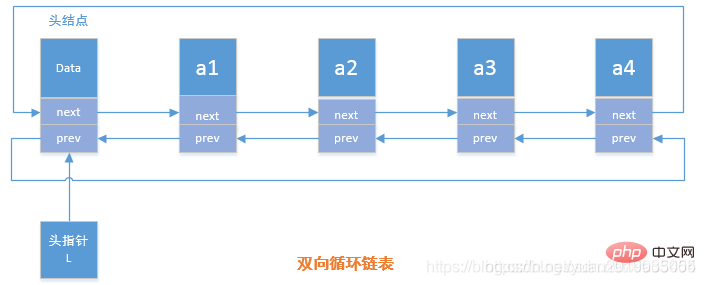
双向循环链表操作
实现类:
public class DoubleNode {
//上一个节点
DoubleNode pre = this;
//下一个节点
DoubleNode next = this;
//节点数据
int data;
public DoubleNode(int data) {
this.data = data;
}
//增加节点
public void after(DoubleNode node) {
//原来的下一个节点
DoubleNode nextNext = next;
//新节点作为当前节点的下一个节点
this.next = node;
//当前节点作为新节点的前一个节点
node.pre = this;
//原来的下一个节点作为新节点的下一个节点
node.next = nextNext;
//原来的下一个节点的上一个节点为新节点
nextNext.pre = node;
}
//获取下一个节点
public DoubleNode getNext() {
return this.next;
}
//获取上一个节点
public DoubleNode getPre() {
return this.pre;
}
//获取数据
public int getData() {
return this.data;
}}
测试类:
public class Demo {
public static void main(String[] args) {
//创建节点
DoubleNode n1 = new DoubleNode(1);
DoubleNode n2 = new DoubleNode(2);
DoubleNode n3 = new DoubleNode(3);
//追加节点
n1.after(n2);
n2.after(n3);
//查看上一个,自己,下一个节点内容
System.out.println(n2.getPre().getData()); //1
System.out.println(n2.getData()); //2
System.out.println(n2.getNext().getData()); //3
System.out.println(n1.getPre().getData()); //3
System.out.println(n3.getNext().getData()); //1
}}
第6章 树结构基础
6.1 为什么要使用树结构
线性结构中不论是数组还是链表,他们都存在着诟病;比如查找某个数必须从头开始查,消耗较多的时间。使用树结构,在插入和查找的性能上相对都会比线性结构要好
6.2 树结构基本概念
示意图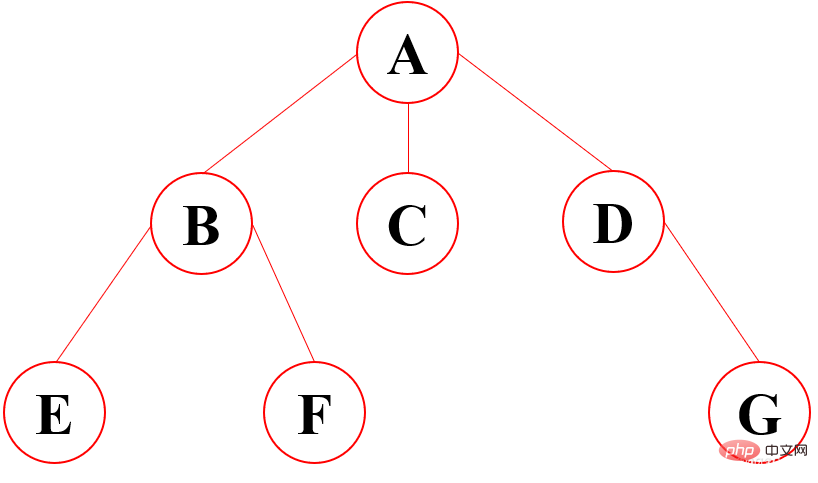
1、根节点:最顶上的唯一的一个;如:A
2、双亲节点:子节点的父节点就叫做双亲节点;如A是B、C、D的双亲节点,B是E、F的双亲节点
3、子节点:双亲节点所产生的节点就是子节点
4、路径:从根节点到目标节点所走的路程叫做路径;如A要访问F,路径为A-B-F
5、节点的度:有多少个子节点就有多少的度(最下面的度一定为0,所以是叶子节点)
6、节点的权:在节点中所存的数字
7、叶子节点:没有子节点的节点,就是没有下一代的节点;如:E、F、C、G
8、子树:在整棵树中将一部分看成也是一棵树,即使只有一个节点也是一棵树,不过这个树是在整个大树职中的,包含的关系
9、层:就是族谱中有多少代的人;如:A是1,B、C、D是2,E、F、G是3
10、树的高度:树的最大的层数:就是层数中的最大值
11、森林:多个树组成的集合
6.3 树的种类
无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树;
有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树;
-
二叉树:每个节点最多含有两个子树的树称为二叉树;
- 完全二叉树:对于一颗二叉树,假设其深度为d(d>1)。除了第d层外,其它各层的节点数目均已达最大值,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树,其中满二叉树的定义是所有叶节点都在最底层的完全二叉树;
- 平衡二叉树(AVL树):当且仅当任何节点的两棵子树的高度差不大于1的二叉树;
- 排序二叉树(二叉查找树(英语:Binary Search Tree),也称二叉搜索树、有序二叉树);
- 霍夫曼树(用于信息编码):带权路径最短的二叉树称为哈夫曼树或最优二叉树;
- B树:一种对读写操作进行优化的自平衡的二叉查找树,能够保持数据有序,拥有多余两个子树。
6.4 树的存储与表示
顺序存储:将数据结构存储在固定的数组中,然在遍历速度上有一定的优势,但因所占空间比较大,是非主流二叉树。二叉树通常以链式存储。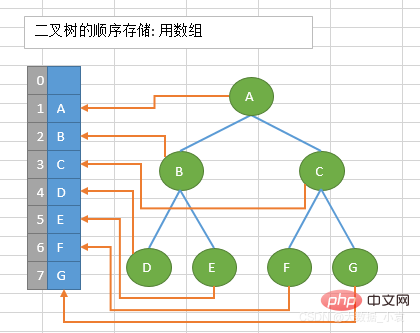
链式存储: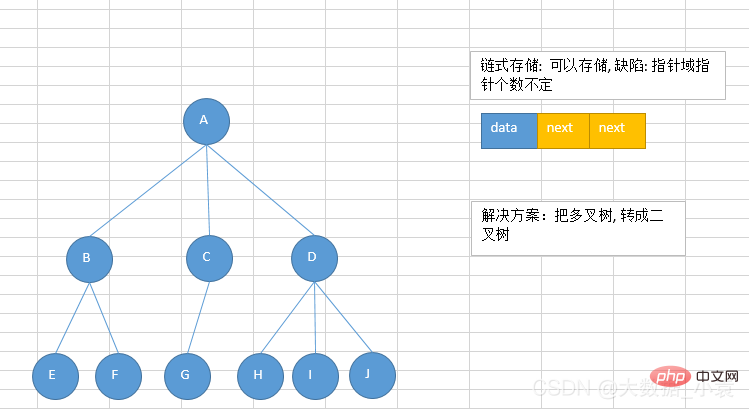
由于对节点的个数无法掌握,常见树的存储表示都转换成二叉树进行处理,子节点个数最多为2
6.5 常见的一些树的应用场景
1、xml,html等,那么编写这些东西的解析器的时候,不可避免用到树
2、路由协议就是使用了树的算法
3、mysql数据库索引
4、文件系统的目录结构
5、所以很多经典的AI算法其实都是树搜索,此外机器学习中的decision tree也是树结构
第7章 二叉树大全
7.1 二叉树的定义
任何一个节点的子节点数量不超过 2,那就是二叉树;二叉树的子节点分为左节点和右节点,不能颠倒位置
7.2 二叉树的性质(特性)
性质1:在二叉树的第i层上至多有2^(i-1)个结点(i>0)
性质2:深度为k的二叉树至多有2^k - 1个结点(k>0)
性质3:对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0=N2+1;
性质4:具有n个结点的完全二叉树的深度必为 log2(n+1)
性质5:对完全二叉树,若从上至下、从左至右编号,则编号为i 的结点,其左孩子编号必为2i,其右孩子编号必为2i+1;其双亲的编号必为i/2(i=1 时为根,除外)
7.3 满二叉树与完全二叉树
满二叉树: 所有叶子结点都集中在二叉树的最下面一层上,而且结点总数为:2^n-1 (n为层数 / 高度)
完全二叉树: 所有的叶子节点都在最后一层或者倒数第二层,且最后一层叶子节点在左边连续,倒数第二层在右边连续(满二叉树也是属于完全二叉树)(从上往下,从左往右能挨着数满)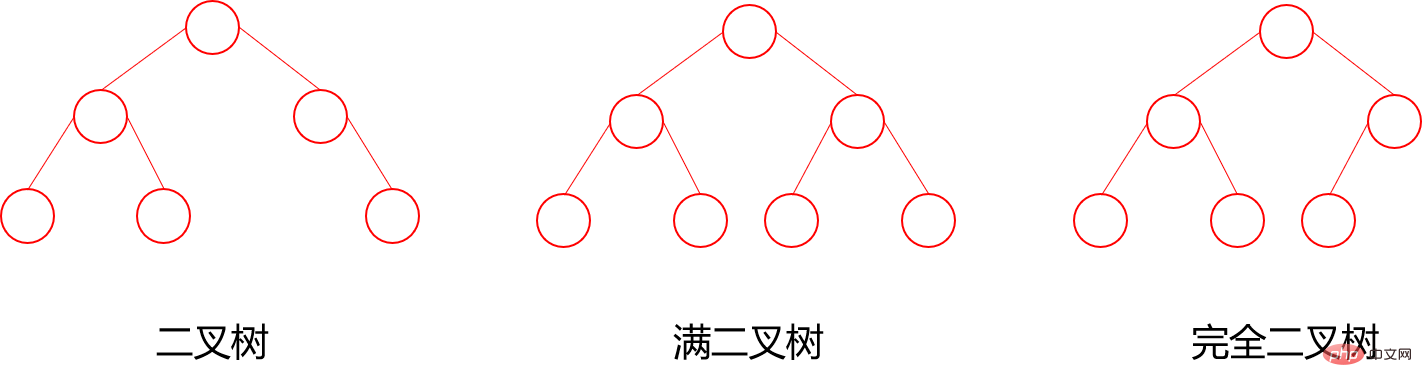
7.4 链式存储的二叉树
创建二叉树:首先需要一个树的类,还需要另一个类用来存放节点,设置节点;将节点放入树中,就形成了二叉树;(节点中需要权值,左子树,右子树,并且都能对他们的值进行设置)。
树的遍历:
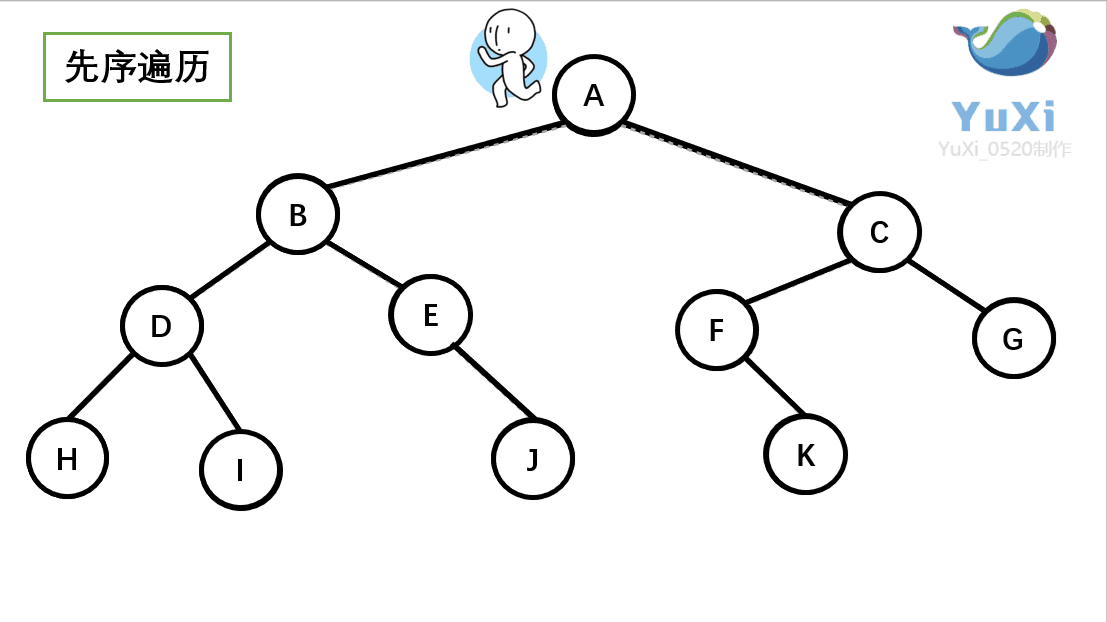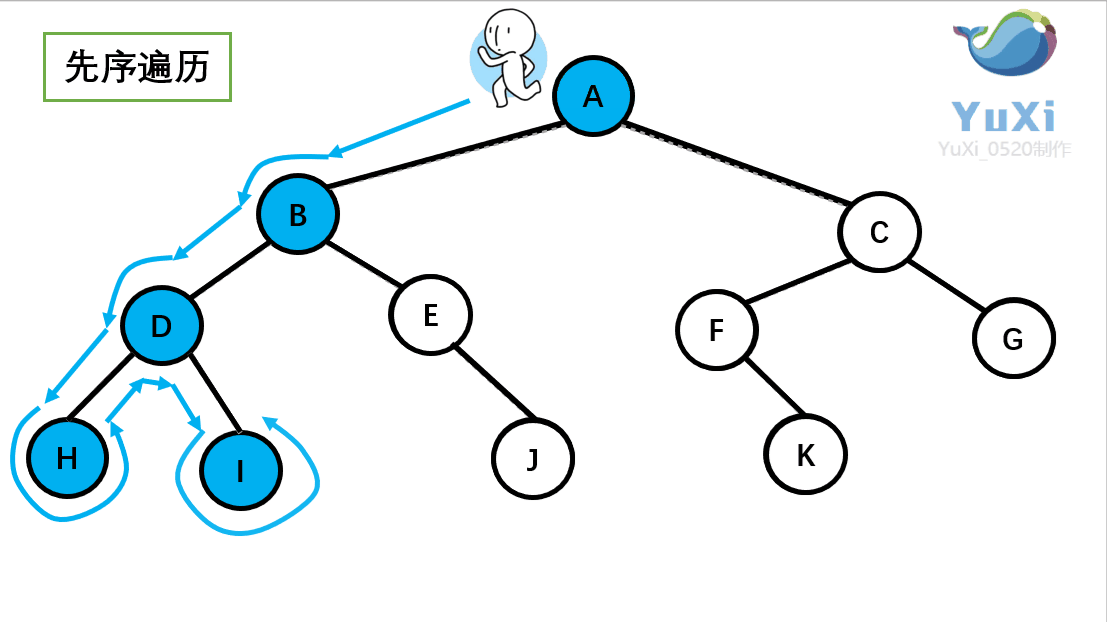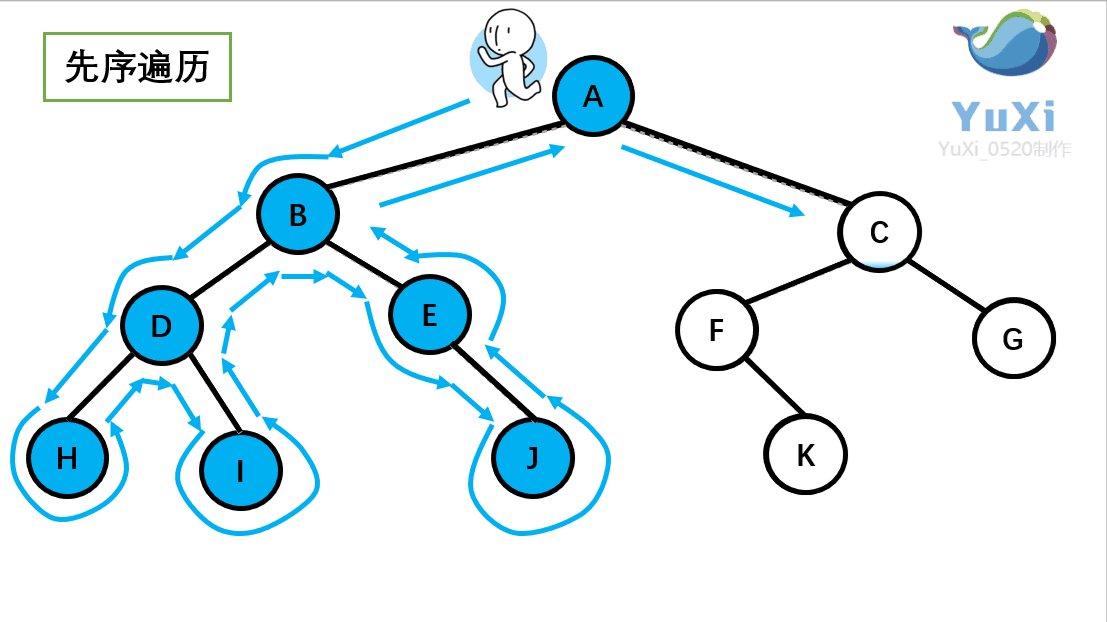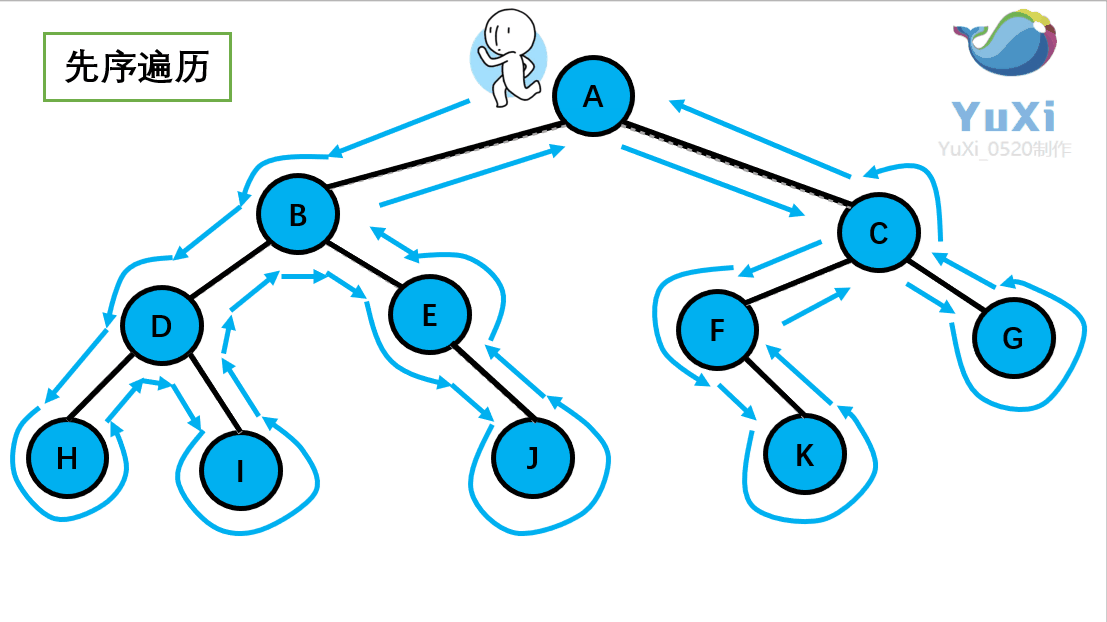
-
先序遍历:根节点,左节点,右节点(如果节点有子树,先从左往右遍历子树,再遍历兄弟节点)
先序遍历结果为:A B D H I E J C F K G
-
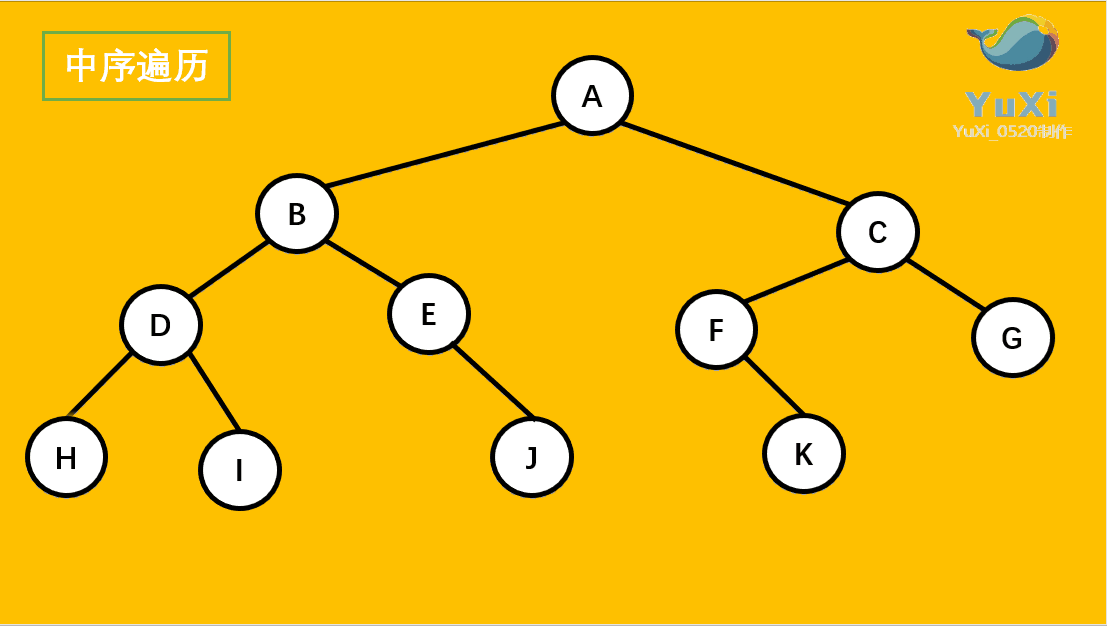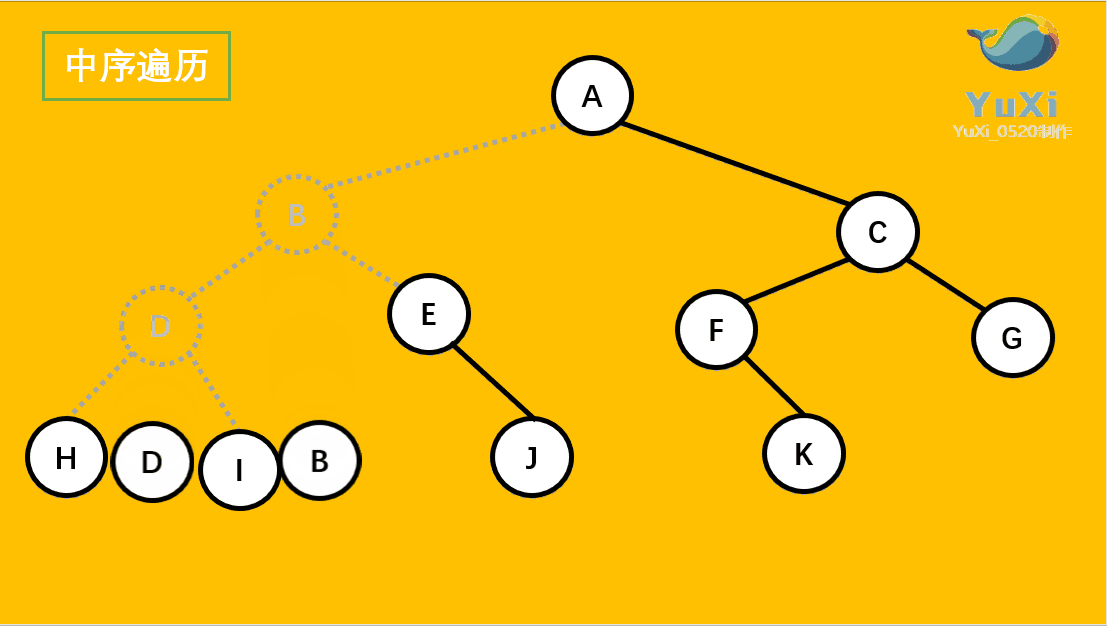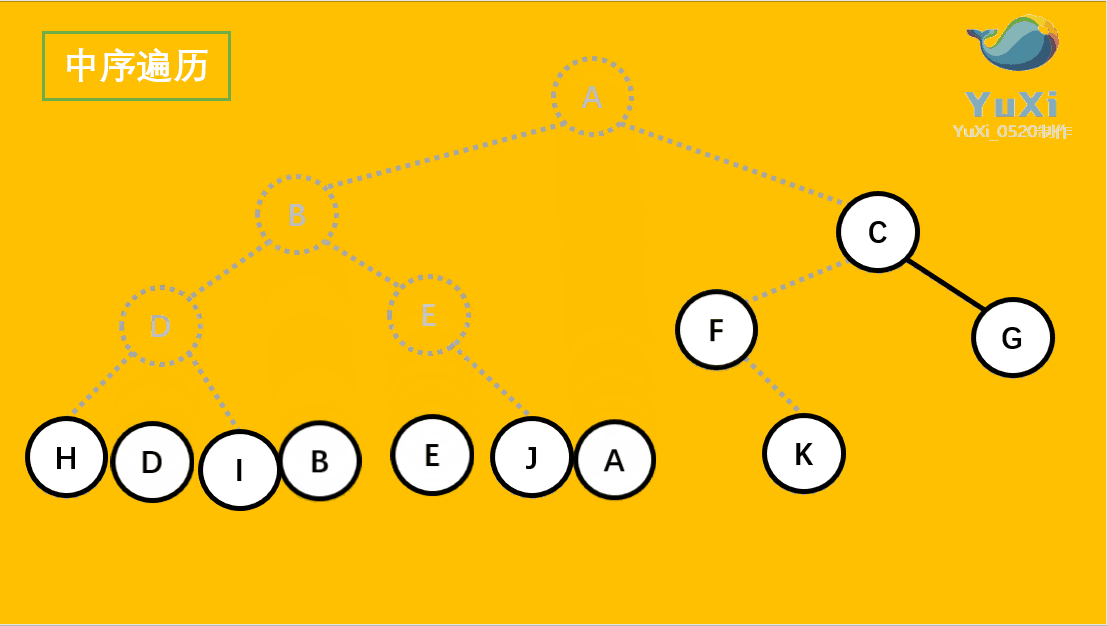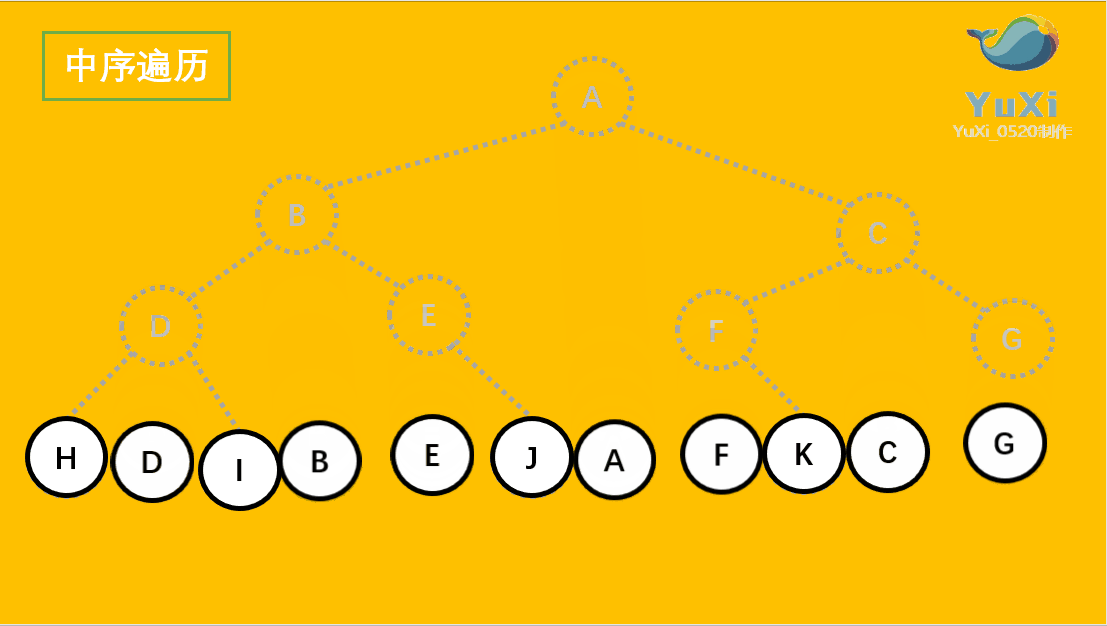
中序遍历:左节点,根节点,右节点(中序遍历可以看成,二叉树每个节点,垂直方向投影下来(可以理解为每个节点从最左边开始垂直掉到地上),然后从左往右数)
中遍历结果为:H D I B E J A F K C G
-
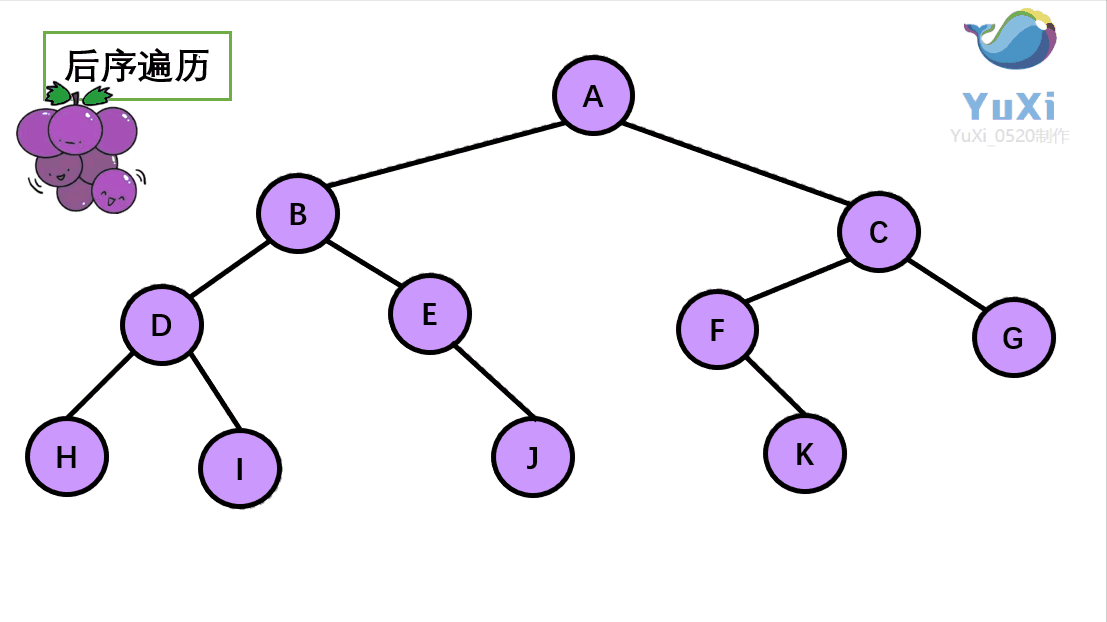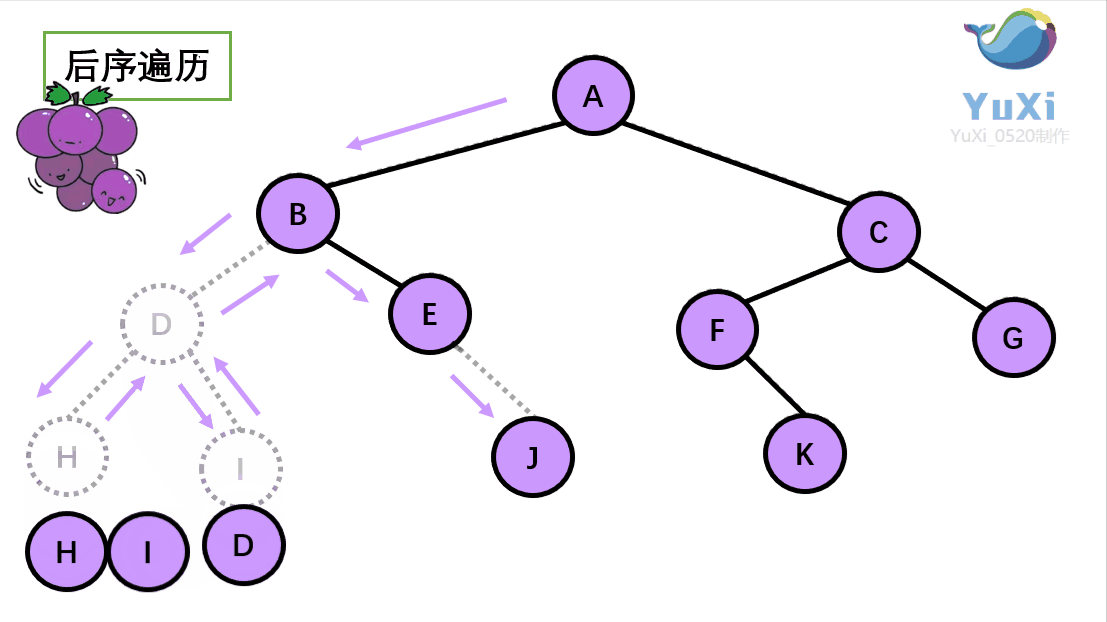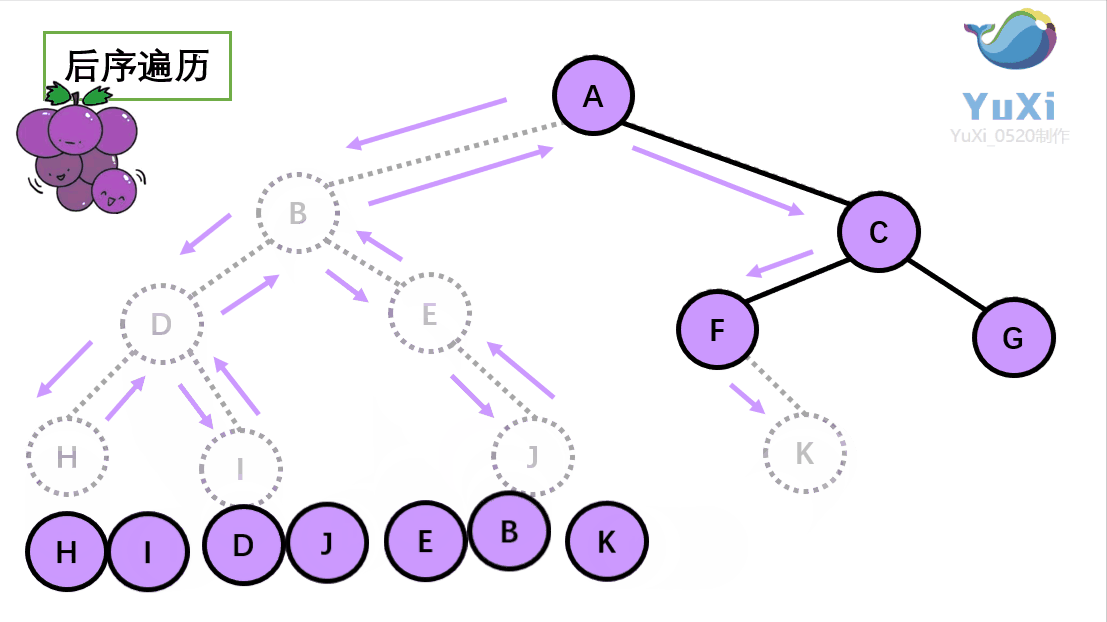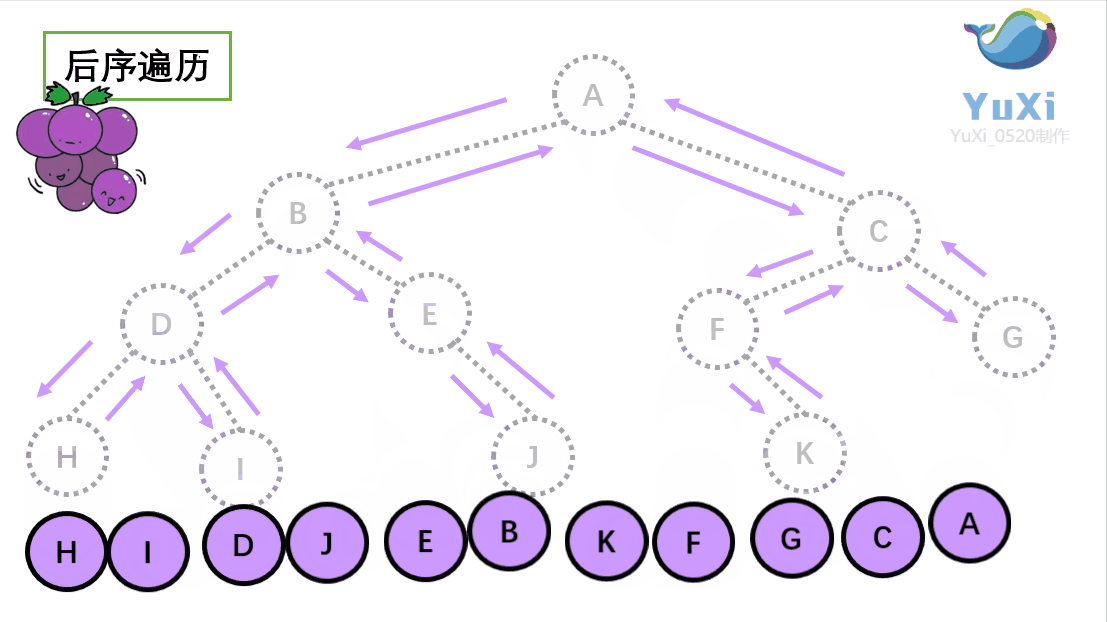
后序遍历:左节点,右节点,根节点
后序遍历结果:H I D J E B K F G C A
-
层次遍历:从上往下,从左往右
层次遍历结果:A B C D E F G H I J K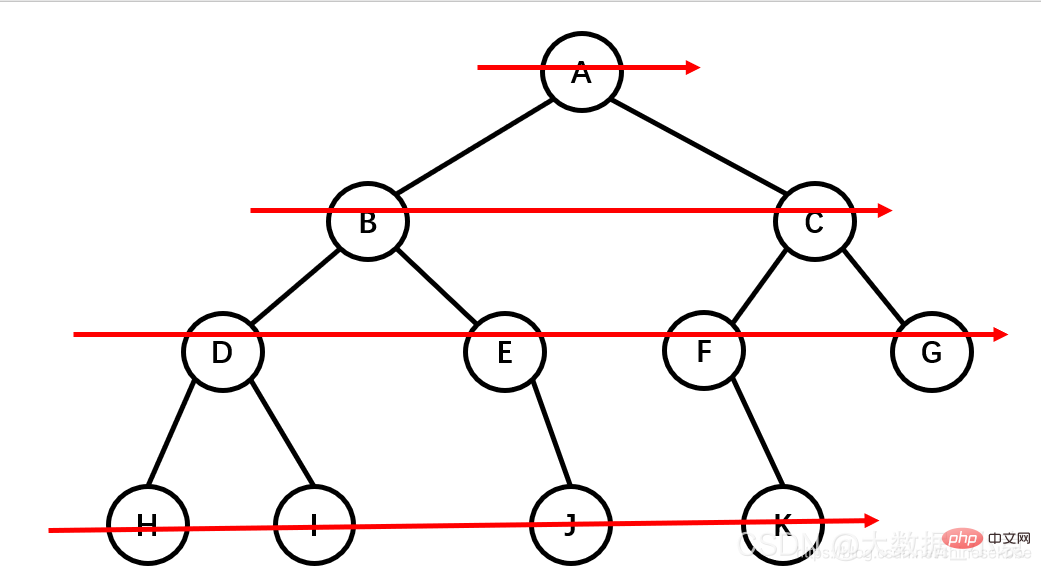
查找节点:先对树进行一次遍历,然后找出要找的那个数;因为有三种排序方法,所以查找节点也分为先序查找,中序查找,后序查找;
删除节点:由于链式存储,不能找到要删的数直接删除,需要找到他的父节点,然后将指向该数设置为null;所以需要一个变量来指向父节点,找到数后,再断开连接。
代码实现:
- 树类
public class BinaryTree {
TreeNode root;
//设置根节点
public void setRoot(TreeNode root) {
this.root = root;
}
//获取根节点
public TreeNode getRoot() {
return root;
}
//先序遍历
public void frontShow() {
if (root != null) {
root.frontShow();
}
}
//中序遍历
public void middleShow() {
if (root != null) {
root.middleShow();
}
}
//后序遍历
public void afterShow() {
if (root != null) {
root.afterShow();
}
}
//先序查找
public TreeNode frontSearch(int i) {
return root.frontSearch(i);
}
//删除一个子树
public void delete(int i) {
if (root.value == i) {
root = null;
} else {
root.delete(i);
}
}}
- 节点类
public class TreeNode {
//节点的权
int value;
//左儿子
TreeNode leftNode;
//右儿子
TreeNode rightNode;
public TreeNode(int value) {
this.value = value;
}
//设置左儿子
public void setLeftNode(TreeNode leftNode) {
this.leftNode = leftNode;
}
//设置右儿子
public void setRightNode(TreeNode rightNode) {
this.rightNode = rightNode;
}
//先序遍历
public void frontShow() {
//先遍历当前节点的值
System.out.print(value + " ");
//左节点
if (leftNode != null) {
leftNode.frontShow(); //递归思想
}
//右节点
if (rightNode != null) {
rightNode.frontShow();
}
}
//中序遍历
public void middleShow() {
//左节点
if (leftNode != null) {
leftNode.middleShow(); //递归思想
}
//先遍历当前节点的值
System.out.print(value + " ");
//右节点
if (rightNode != null) {
rightNode.middleShow();
}
}
//后续遍历
public void afterShow() {
//左节点
if (leftNode != null) {
leftNode.afterShow(); //递归思想
}
//右节点
if (rightNode != null) {
rightNode.afterShow();
}
//先遍历当前节点的值
System.out.print(value + " ");
}
//先序查找
public TreeNode frontSearch(int i) {
TreeNode target = null;
//对比当前节点的值
if (this.value == i) {
return this;
//当前节点不是要查找的节点
} else {
//查找左儿子
if (leftNode != null) {
//查找的话t赋值给target,查不到target还是null
target = leftNode.frontSearch(i);
}
//如果target不为空,说明在左儿子中已经找到
if (target != null) {
return target;
}
//如果左儿子没有查到,再查找右儿子
if (rightNode != null) {
target = rightNode.frontSearch(i);
}
}
return target;
}
//删除一个子树
public void delete(int i) {
TreeNode parent = this;
//判断左儿子
if (parent.leftNode != null && parent.leftNode.value == i) {
parent.leftNode = null;
return;
}
//判断右儿子
if (parent.rightNode != null && parent.rightNode.value == i) {
parent.rightNode = null;
return;
}
//如果都不是,递归检查并删除左儿子
parent = leftNode;
if (parent != null) {
parent.delete(i);
}
//递归检查并删除右儿子
parent = rightNode;
if (parent != null) {
parent.delete(i);
}
}}
- 测试类
public class Demo {
public static void main(String[] args) {
//创建一棵树
BinaryTree binaryTree = new BinaryTree();
//创建一个根节点
TreeNode root = new TreeNode(1);
//把根节点赋给树
binaryTree.setRoot(root);
//创建左,右节点
TreeNode rootLeft = new TreeNode(2);
TreeNode rootRight = new TreeNode(3);
//把新建的节点设置为根节点的子节点
root.setLeftNode(rootLeft);
root.setRightNode(rootRight);
//为第二层的左节点创建两个子节点
rootLeft.setLeftNode(new TreeNode(4));
rootLeft.setRightNode(new TreeNode(5));
//为第二层的右节点创建两个子节点
rootRight.setLeftNode(new TreeNode(6));
rootRight.setRightNode(new TreeNode(7));
//先序遍历
binaryTree.frontShow(); //1 2 4 5 3 6 7
System.out.println();
//中序遍历
binaryTree.middleShow(); //4 2 5 1 6 3 7
System.out.println();
//后序遍历
binaryTree.afterShow(); //4 5 2 6 7 3 1
System.out.println();
//先序查找
TreeNode result = binaryTree.frontSearch(5);
System.out.println(result); //binarytree.TreeNode@1b6d3586
//删除一个子树
binaryTree.delete(2);
binaryTree.frontShow(); //1 3 6 7 ,2和他的子节点被删除了
}}
7.5 顺序存储的二叉树

概述:顺序存储使用数组的形式实现;由于非完全二叉树会导致数组中出现空缺,有的位置不能填上数字,所以顺序存储二叉树通常情况下只考虑完全二叉树
原理: 顺序存储在数组中是按照第一层第二层一次往下存储的,遍历方式也有先序遍历、中序遍历、后续遍历
性质:
- 第n个元素的左子节点是:2*n+1;
- 第n个元素的右子节点是:2*n+2;
- 第n个元素的父节点是:(n-1)/2
代码实现:
- 树类
public class ArrayBinaryTree {
int[] data;
public ArrayBinaryTree(int[] data) {
this.data = data;
}
//重载先序遍历方法,不用每次传参数了,保证每次从头开始
public void frontShow() {
frontShow(0);
}
//先序遍历
public void frontShow(int index) {
if (data == null || data.length == 0) {
return;
}
//先遍历当前节点的内容
System.out.print(data[index] + " ");
//处理左子树:2*index+1
if (2 * index + 1
- 测试类
public class Demo {
public static void main(String[] args) {
int[] data = {1,2,3,4,5,6,7};
ArrayBinaryTree tree = new ArrayBinaryTree(data);
//先序遍历
tree.frontShow(); //1 2 4 5 3 6 7
}}
7.6 线索二叉树(Threaded BinaryTree)
为什么使用线索二叉树?
当用二叉链表作为二叉树的存储结构时,可以很方便的找到某个结点的左右孩子;但一般情况下,无法直接找到该结点在某种遍历序列中的前驱和后继结点
原理:n个结点的二叉链表中含有n+1(2n-(n-1)=n+1个空指针域。利用二叉链表中的空指针域,存放指向结点在某种遍历次序下的前驱和后继结点的指针。
例如:某个结点的左孩子为空,则将空的左孩子指针域改为指向其前驱;如果某个结点的右孩子为空,则将空的右孩子指针域改为指向其后继(这种附加的指针称为"线索")
代码实现:
- 树类
public class ThreadedBinaryTree {
ThreadedNode root;
//用于临时存储前驱节点
ThreadedNode pre = null;
//设置根节点
public void setRoot(ThreadedNode root) {
this.root = root;
}
//中序线索化二叉树
public void threadNodes() {
threadNodes(root);
}
public void threadNodes(ThreadedNode node) {
//当前节点如果为null,直接返回
if (node == null) {
return;
}
//处理左子树
threadNodes(node.leftNode);
//处理前驱节点
if (node.leftNode == null) {
//让当前节点的左指针指向前驱节点
node.leftNode = pre;
//改变当前节点左指针类型
node.leftType = 1;
}
//处理前驱的右指针,如果前驱节点的右指针是null(没有右子树)
if (pre != null && pre.rightNode == null) {
//让前驱节点的右指针指向当前节点
pre.rightNode = node;
//改变前驱节点的右指针类型
pre.rightType = 1;
}
//每处理一个节点,当前节点是下一个节点的前驱节点
pre = node;
//处理右子树
threadNodes(node.rightNode);
}
//遍历线索二叉树
public void threadIterate() {
//用于临时存储当前遍历节点
ThreadedNode node = root;
while (node != null) {
//循环找到最开始的节点
while (node.leftType == 0) {
node = node.leftNode;
}
//打印当前节点的值
System.out.print(node.value + " ");
//如果当前节点的右指针指向的是后继节点,可能后继节点还有后继节点
while (node.rightType == 1) {
node = node.rightNode;
System.out.print(node.value + " ");
}
//替换遍历的节点
node = node.rightNode;
}
}
//获取根节点
public ThreadedNode getRoot() {
return root;
}
//先序遍历
public void frontShow() {
if (root != null) {
root.frontShow();
}
}
//中序遍历
public void middleShow() {
if (root != null) {
root.middleShow();
}
}
//后序遍历
public void afterShow() {
if (root != null) {
root.afterShow();
}
}
//先序查找
public ThreadedNode frontSearch(int i) {
return root.frontSearch(i);
}
//删除一个子树
public void delete(int i) {
if (root.value == i) {
root = null;
} else {
root.delete(i);
}
}}
- 节点类
public class ThreadedNode {
//节点的权
int value;
//左儿子
ThreadedNode leftNode;
//右儿子
ThreadedNode rightNode;
//标识指针类型,1表示指向上一个节点,0
int leftType;
int rightType;
public ThreadedNode(int value) {
this.value = value;
}
//设置左儿子
public void setLeftNode(ThreadedNode leftNode) {
this.leftNode = leftNode;
}
//设置右儿子
public void setRightNode(ThreadedNode rightNode) {
this.rightNode = rightNode;
}
//先序遍历
public void frontShow() {
//先遍历当前节点的值
System.out.print(value + " ");
//左节点
if (leftNode != null) {
leftNode.frontShow(); //递归思想
}
//右节点
if (rightNode != null) {
rightNode.frontShow();
}
}
//中序遍历
public void middleShow() {
//左节点
if (leftNode != null) {
leftNode.middleShow(); //递归思想
}
//先遍历当前节点的值
System.out.print(value + " ");
//右节点
if (rightNode != null) {
rightNode.middleShow();
}
}
//后续遍历
public void afterShow() {
//左节点
if (leftNode != null) {
leftNode.afterShow(); //递归思想
}
//右节点
if (rightNode != null) {
rightNode.afterShow();
}
//先遍历当前节点的值
System.out.print(value + " ");
}
//先序查找
public ThreadedNode frontSearch(int i) {
ThreadedNode target = null;
//对比当前节点的值
if (this.value == i) {
return this;
//当前节点不是要查找的节点
} else {
//查找左儿子
if (leftNode != null) {
//查找的话t赋值给target,查不到target还是null
target = leftNode.frontSearch(i);
}
//如果target不为空,说明在左儿子中已经找到
if (target != null) {
return target;
}
//如果左儿子没有查到,再查找右儿子
if (rightNode != null) {
target = rightNode.frontSearch(i);
}
}
return target;
}
//删除一个子树
public void delete(int i) {
ThreadedNode parent = this;
//判断左儿子
if (parent.leftNode != null && parent.leftNode.value == i) {
parent.leftNode = null;
return;
}
//判断右儿子
if (parent.rightNode != null && parent.rightNode.value == i) {
parent.rightNode = null;
return;
}
//如果都不是,递归检查并删除左儿子
parent = leftNode;
if (parent != null) {
parent.delete(i);
}
//递归检查并删除右儿子
parent = rightNode;
if (parent != null) {
parent.delete(i);
}
}}
- 测试类
public class Demo {
public static void main(String[] args) {
//创建一棵树
ThreadedBinaryTree binaryTree = new ThreadedBinaryTree();
//创建一个根节点
ThreadedNode root = new ThreadedNode(1);
//把根节点赋给树
binaryTree.setRoot(root);
//创建左,右节点
ThreadedNode rootLeft = new ThreadedNode(2);
ThreadedNode rootRight = new ThreadedNode(3);
//把新建的节点设置为根节点的子节点
root.setLeftNode(rootLeft);
root.setRightNode(rootRight);
//为第二层的左节点创建两个子节点
rootLeft.setLeftNode(new ThreadedNode(4));
ThreadedNode fiveNode = new ThreadedNode(5);
rootLeft.setRightNode(fiveNode);
//为第二层的右节点创建两个子节点
rootRight.setLeftNode(new ThreadedNode(6));
rootRight.setRightNode(new ThreadedNode(7));
//中序遍历
binaryTree.middleShow(); //4 2 5 1 6 3 7
System.out.println();
//中序线索化二叉树
binaryTree.threadNodes();// //获取5的后继节点// ThreadedNode afterFive = fiveNode.rightNode;// System.out.println(afterFive.value); //1
binaryTree.threadIterate(); //4 2 5 1 6 3 7
}}
7.7 二叉排序树(Binary Sort Tree)
无序序列: 二叉排序树图解:
二叉排序树图解: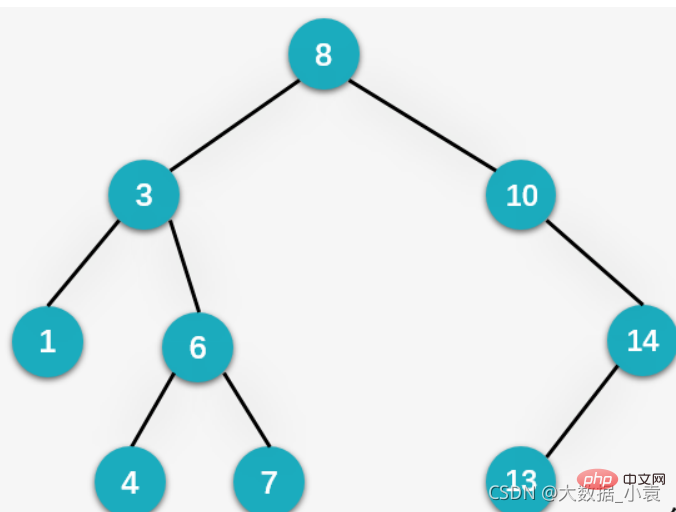
概述:二叉排序树(Binary Sort Tree)也叫二叉查找树或者是一颗空树,对于二叉树中的任何一个非叶子节点,要求左子节点比当前节点值小,右子节点比当前节点值大
特点:
- 查找性能与插入删除性能都适中还不错
- 中序遍历的结果刚好是从大到小
创建二叉排序树原理:其实就是不断地插入节点,然后进行比较。
删除节点
- 删除叶子节点,只需要找到父节点,将父节点与他的连接断开即可
- 删除有一个子节点的就需要将他的子节点换到他现在的位置
- 删除有两个子节点的节点,需要使用他的前驱节点或者后继节点进行替换,就是左子树最右下方的数(最大的那个)或右子树最左边的树(最小的数);即离节点值最接近的值;(还要注解要去判断这个值有没有右节点,有就要将右节点移上来)
代码实现:
- 树类
public class BinarySortTree {
Node root;
//添加节点
public void add(Node node) {
//如果是一颗空树
if (root == null) {
root = node;
} else {
root.add(node);
}
}
//中序遍历
public void middleShow() {
if (root != null) {
root.middleShow(root);
}
}
//查找节点
public Node search(int value) {
if (root == null) {
return null;
}
return root.search(value);
}
//查找父节点
public Node searchParent(int value) {
if (root == null) {
return null;
}
return root.searchParent(value);
}
//删除节点
public void delete(int value) {
if (root == null) {
return;
} else {
//找到这个节点
Node target = search(value);
//如果没有这个节点
if (target == null) {
return;
}
//找到他的父节点
Node parent = searchParent(value);
//要删除的节点是叶子节点
if (target.left == null && target.left == null) {
//要删除的节点是父节点的左子节点
if (parent.left.value == value) {
parent.left = null;
}
//要删除的节点是父节点的右子节点
else {
parent.right = null;
}
}
//要删除的节点有两个子节点的情况
else if (target.left != null && target.right != null) {
//删除右子树中值最小的节点,并且获取到值
int min = deletMin(target.right);
//替换目标节点中的值
target.value = min;
}
//要删除的节点有一个左子节点或右子节点
else {
//有左子节点
if (target.left != null) {
//要删除的节点是父节点的左子节点
if (parent.left.value == value) {
parent.left = target.left;
}
//要删除的节点是父节点的右子节点
else {
parent.right = target.left;
}
}
//有右子节点
else {
//要删除的节点是父节点的左子节点
if (parent.left.value == value) {
parent.left = target.right;
}
//要删除的节点是父节点的右子节点
else {
parent.right = target.right;
}
}
}
}
}
//删除一棵树中最小的节点
private int deletMin(Node node) {
Node target = node;
//递归向左找最小值
while (target.left != null) {
target = target.left;
}
//删除最小的节点
delete(target.value);
return target.value;
}}
- 节点类
public class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
//向子树中添加节点
public void add(Node node) {
if (node == null) {
return;
}
/*判断传入的节点的值比当前紫薯的根节点的值大还是小*/
//添加的节点比当前节点更小(传给左节点)
if (node.value value && this.left != null) {
return this.left.searchParent(value);
} else if (this.value
- 测试类
public class Demo {
public static void main(String[] args) {
int[] arr = {8, 3, 10, 1, 6, 14, 4, 7, 13};
//创建一颗二叉排序树
BinarySortTree bst = new BinarySortTree();
//循环添加/* for(int i=0;i<h2>7.8 平衡二叉树( Balanced Binary Tree)</h2><h3>为什么使用平衡二叉树?</h3><p>平衡二叉树(Balanced Binary Tree)又被称为AVL树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。这个方案很好的解决了二叉查找树退化成链表的问题,把插入,查找,删除的时间复杂度最好情况和最坏情况都维持在<code>O(logN)</code>。但是频繁旋转会使插入和删除牺牲掉<code>O(logN)</code>左右的时间,不过相对二叉查找树来说,时间上稳定了很多。</p><p>二叉排序树插入 {1,2,3,4,5,6} 这种数据结果如下图所示:<br><img src="https://img.php.cn/upload/article/000/000/067/3ecfcc25f4c8b7a56d063b2b27bace0c-23.png" alt="Javaのデータ構造とアルゴリズムの詳細な図解説明"><br> 平衡二叉树插入 {1,2,3,4,5,6} 这种数据结果如下图所示:<br><img src="https://img.php.cn/upload/article/000/000/067/3ecfcc25f4c8b7a56d063b2b27bace0c-24.png" alt="Javaのデータ構造とアルゴリズムの詳細な図解説明"></p><h3>如何判断平衡二叉树?</h3>
- 1、是二叉排序树
- 2、任何一个节点的左子树或者右子树都是平衡二叉树(左右高度差小于等于 1)
(1)下图不是平衡二叉树,因为它不是二叉排序树违反第 1 条件
(2)下图不是平衡二叉树,因为有节点子树高度差大于 1 违法第 2 条件(5的左子树为0,右子树为2)
(3)下图是平衡二叉树,因为符合 1、2 条件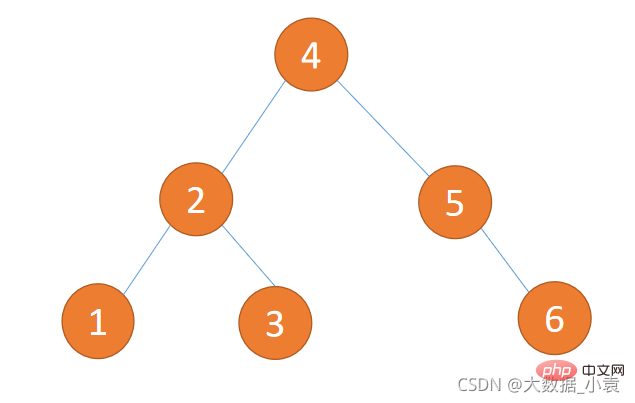
相关概念
平衡因子 BF
- 定義: 左のサブツリーと右のサブツリーの高さの差
- 計算:
左のサブツリーの高さ - 右のサブツリーの高さの値 - 別名: BF (バランス ファクター) と略されます #一般的に、BF の絶対値が 1 より大きい場合、バランス ツリーのバイナリ ツリーはアンバランスになるため、修正するために回転する必要があります
最小の不均衡サブツリー
- #挿入されたノードに最も近く、BF の絶対値が 1 より大きいノードがサブツリーです。ルートノードの。 #回転補正では、最小の不均衡サブツリーのみを補正する必要があります。
- #例を以下の図に示します。
-
##回転方法
2 つの回転方法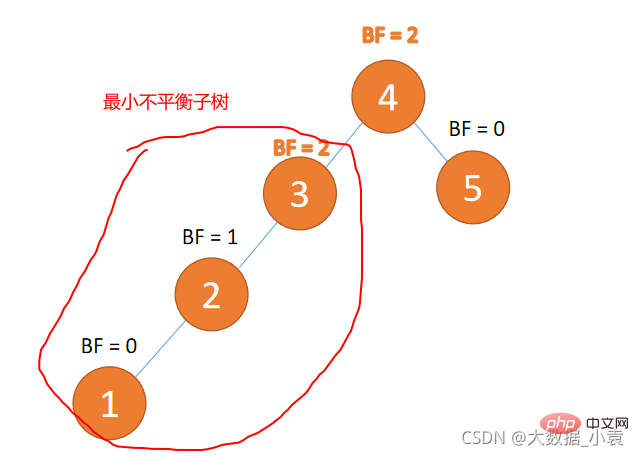 :
:
左回転:
古いルートノードは新しいルート ノードの左側のサブツリーです。
新しいルート ノードの左側のサブツリー (存在する場合) は、古いルート ノードの右側のサブツリーです。- 右回転:
- 古いルート ノードは、新しいルート ノードの右のサブツリーです。
- #4 種類の回転補正
- :
- ##左-左タイプ: 左の子の左サブツリーを挿入、右回転
左-左タイプ: 左の子の右サブツリーを挿入、最初に左に回転し、次に右に回転します
右-左タイプ: 右の子の左サブツリーを挿入し、最初に右に回転し、次に左に回転します- 左-左タイプ :
-
3 番目のノード (1) が挿入されると、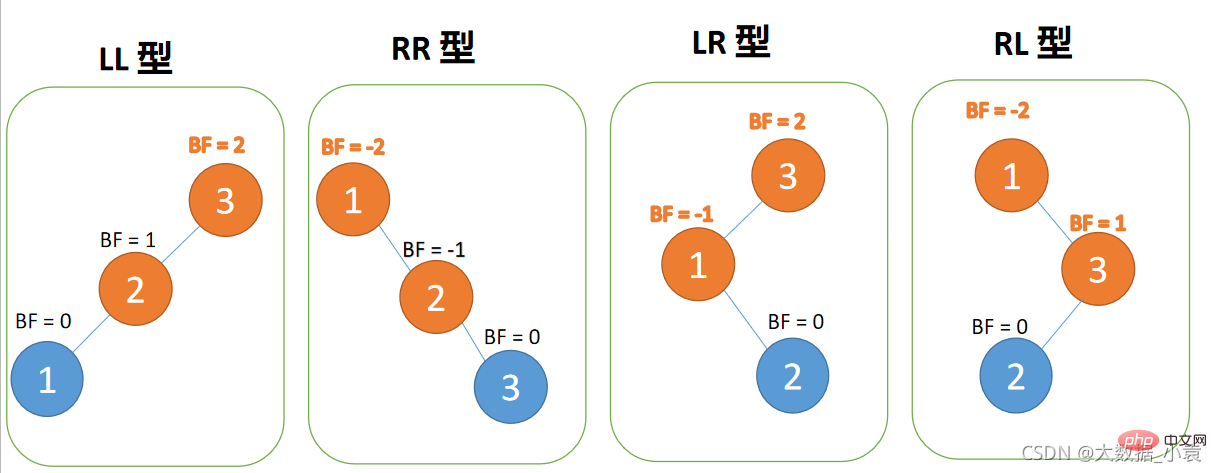 BF(3) = 2、BF(2) = 1 、右手回り、ルート ノードは時計回りに回転します
BF(3) = 2、BF(2) = 1 、右手回り、ルート ノードは時計回りに回転します
左右型
:3番目のノード(3) 挿入時、 BF(1)=-2 BF(2)=-1
、 RR タイプ アンバランス、左利き、ルート ノードが反時計回りに回転 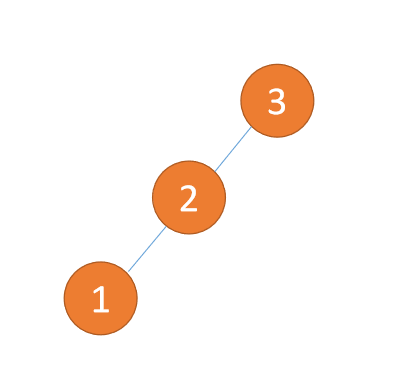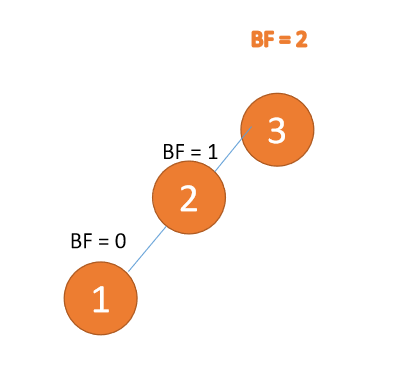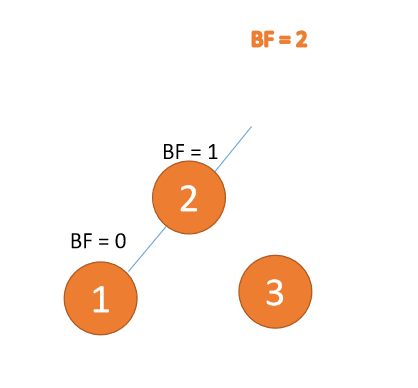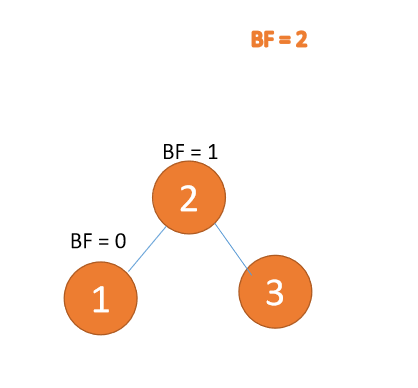
#左右タイプ
3 番目のノード (3) を挿入すると、BF(3)=2 BF(1)=-1
LR タイプのアンバランス、最初は左巻き、次に右巻き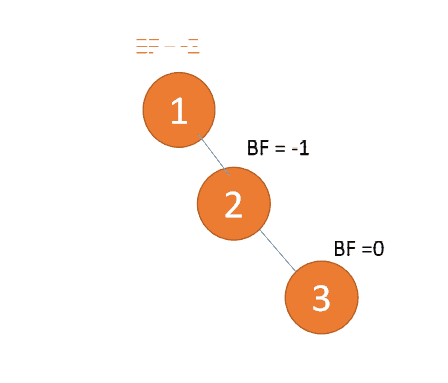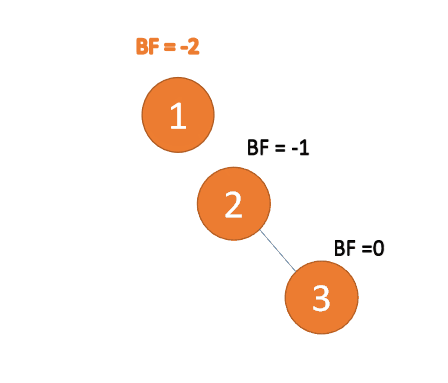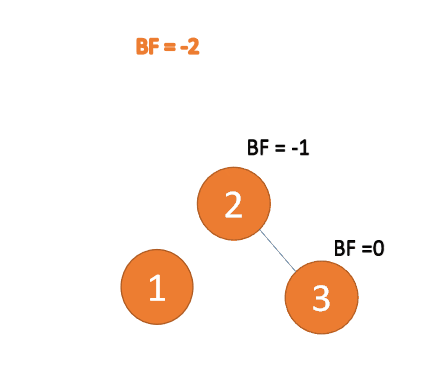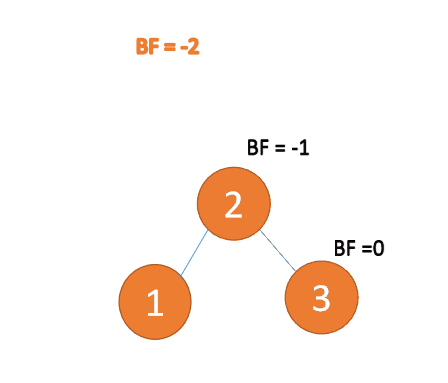
##右- left type:
3 番目のノード (1) を挿入すると、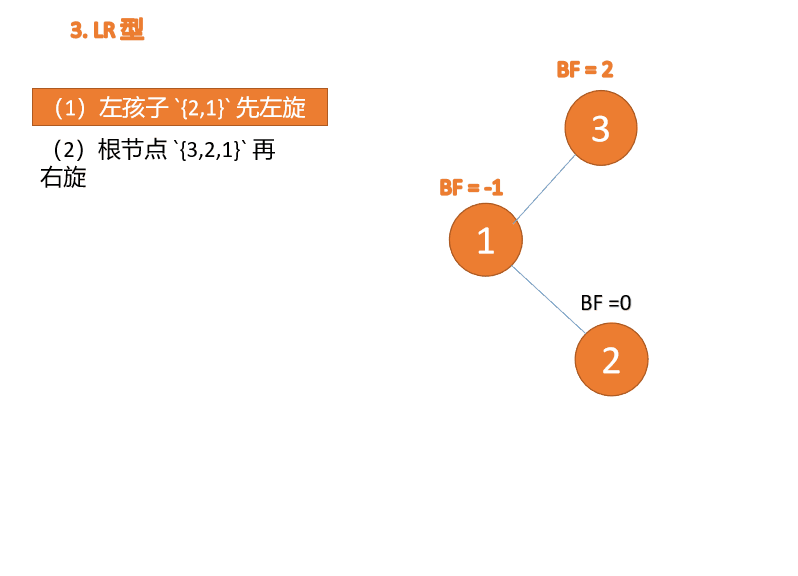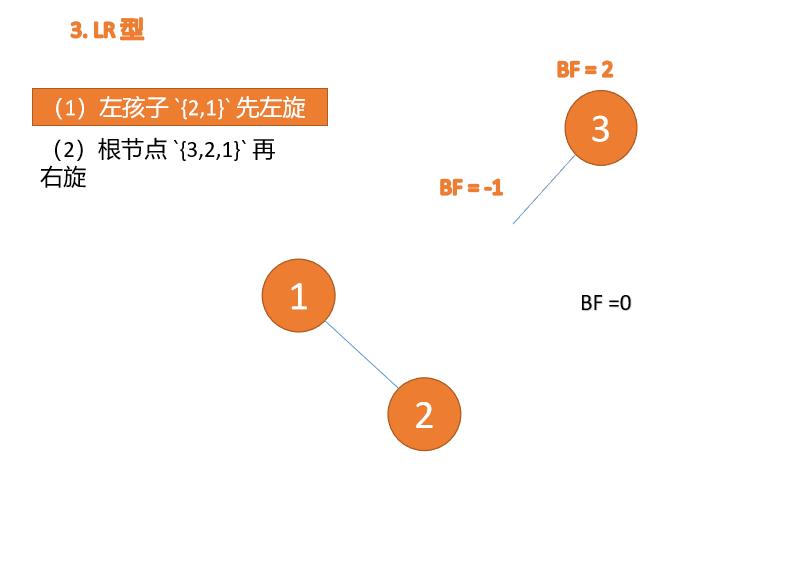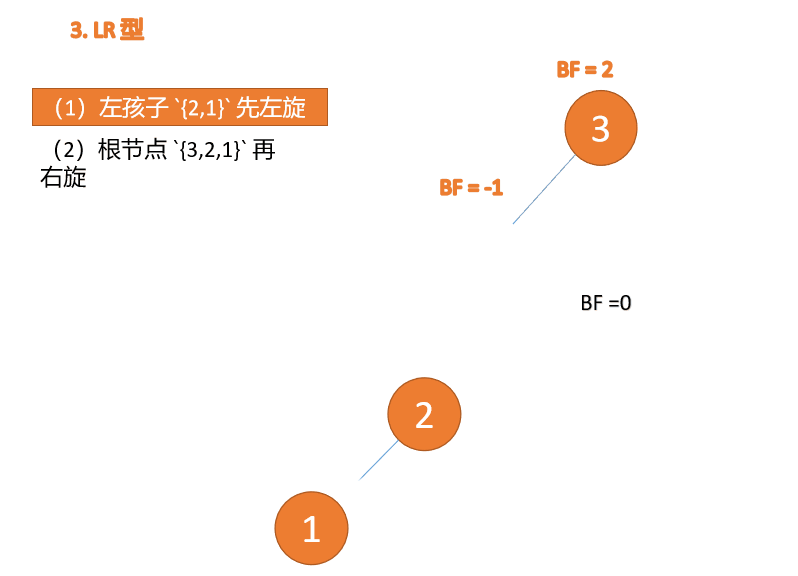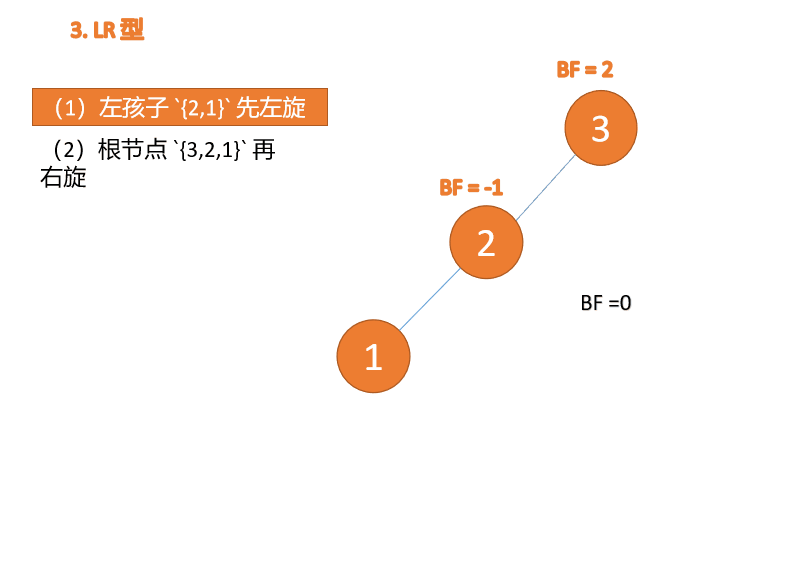 BF(1)=-2 BF(3)=1
BF(1)=-2 BF(3)=1
RL 型アンバランス、最初の右回転その後左回転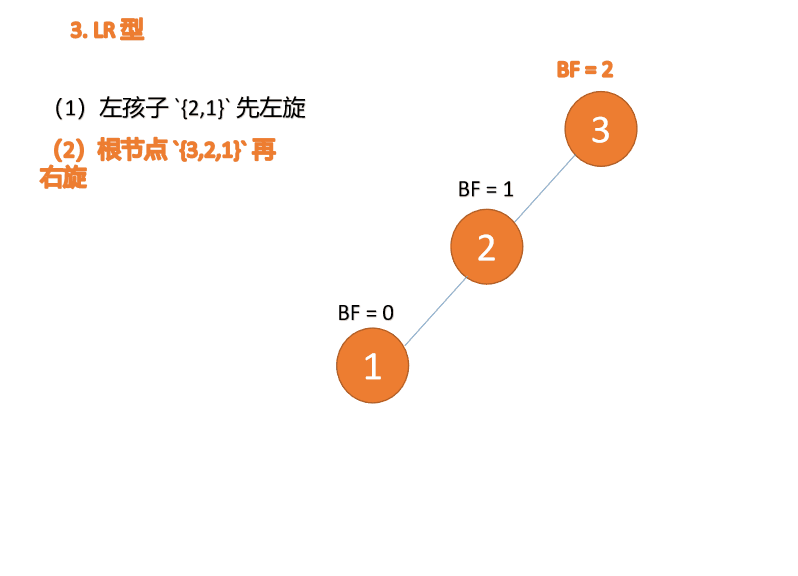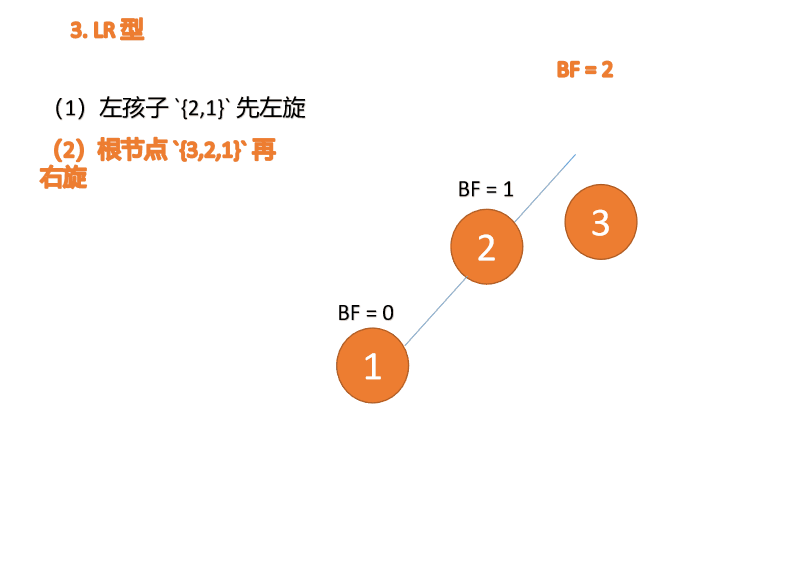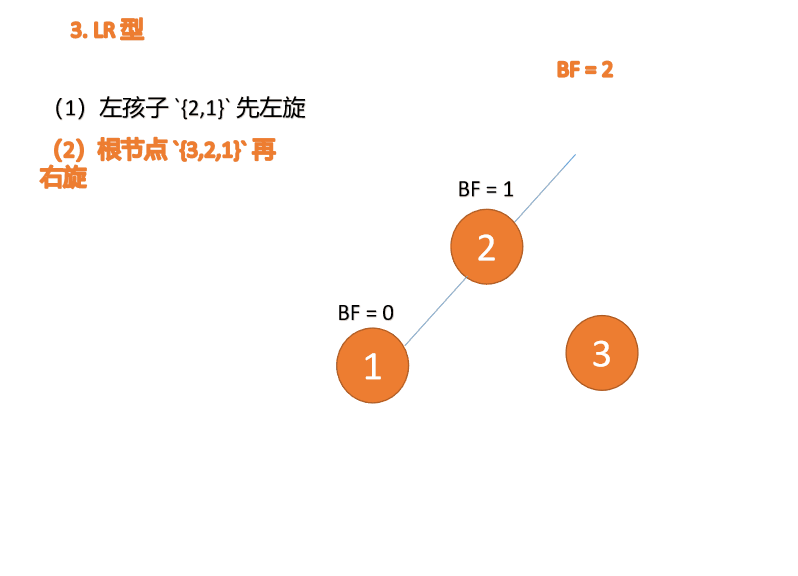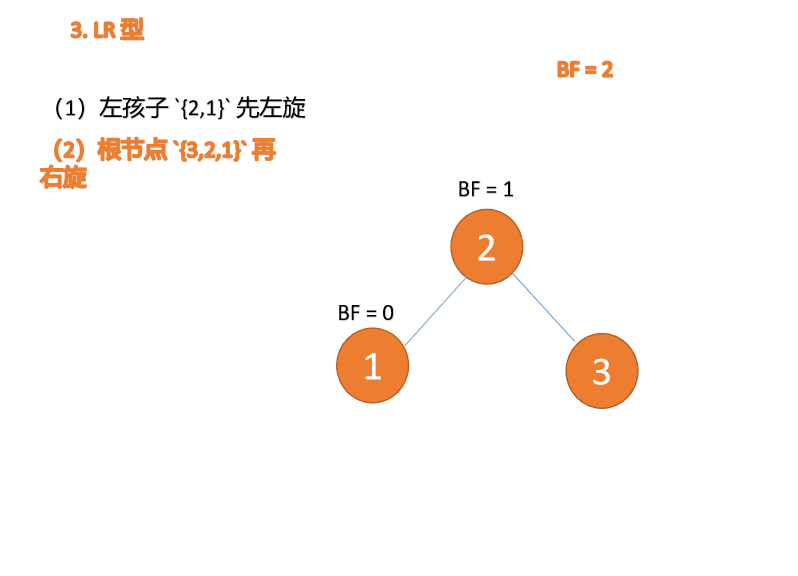
例
BF(3)=2 BF(2)=1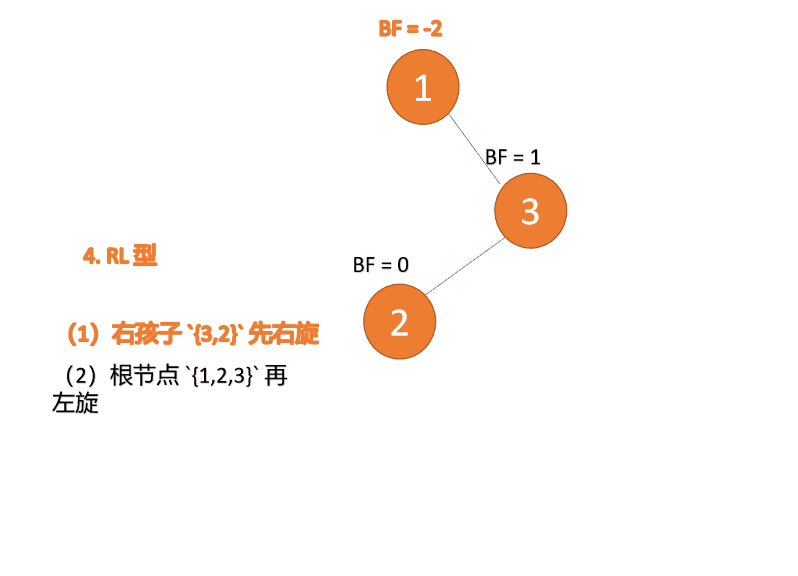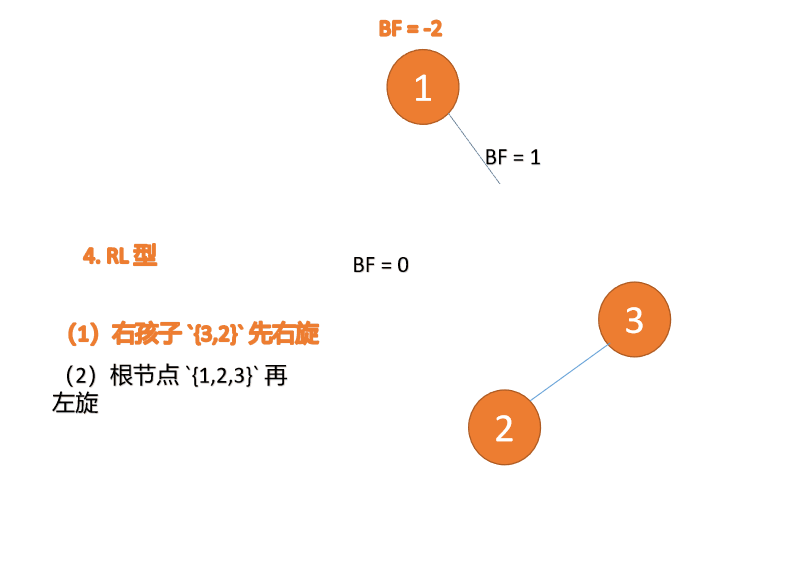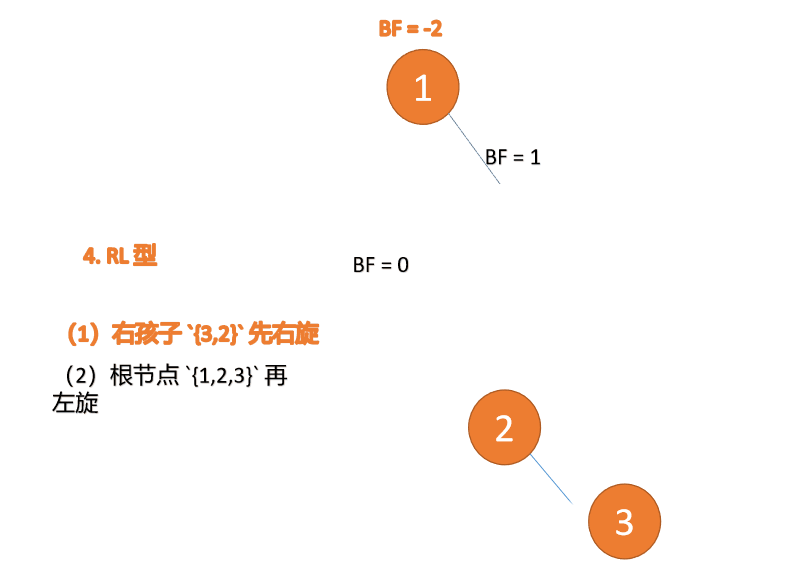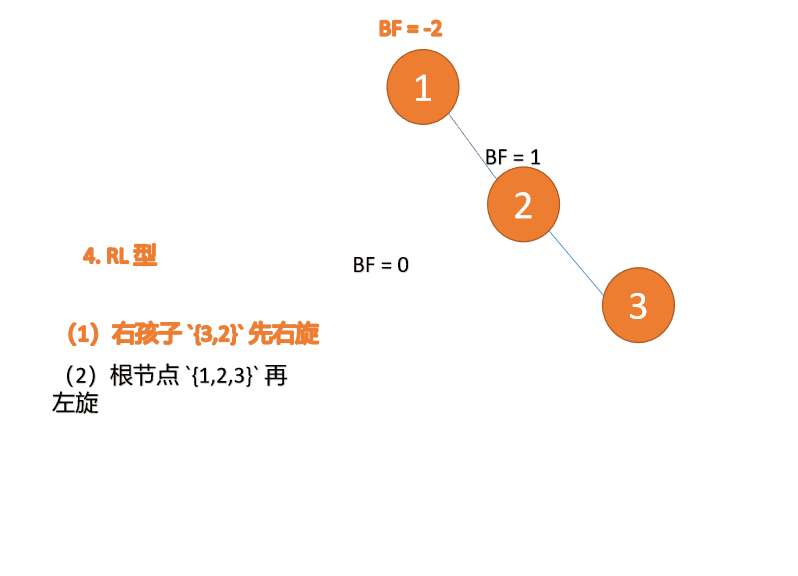 、LL 型不均衡、最小不平衡ツリー {3,2,1} に対して右回転を実行
、LL 型不均衡、最小不平衡ツリー {3,2,1} に対して右回転を実行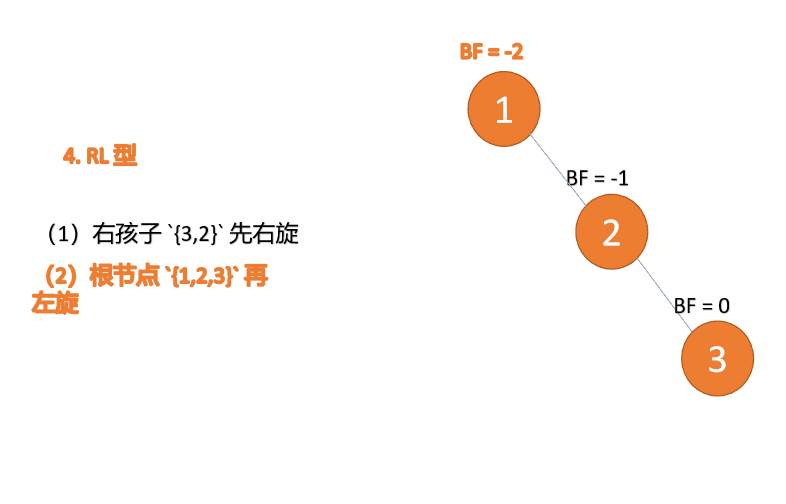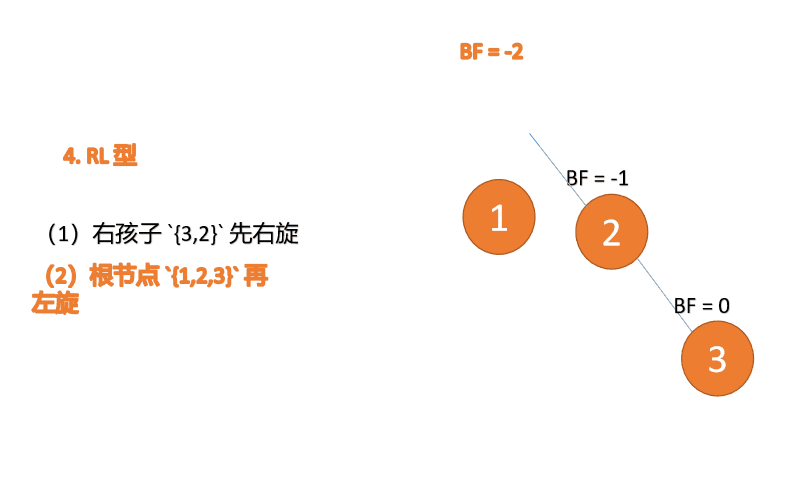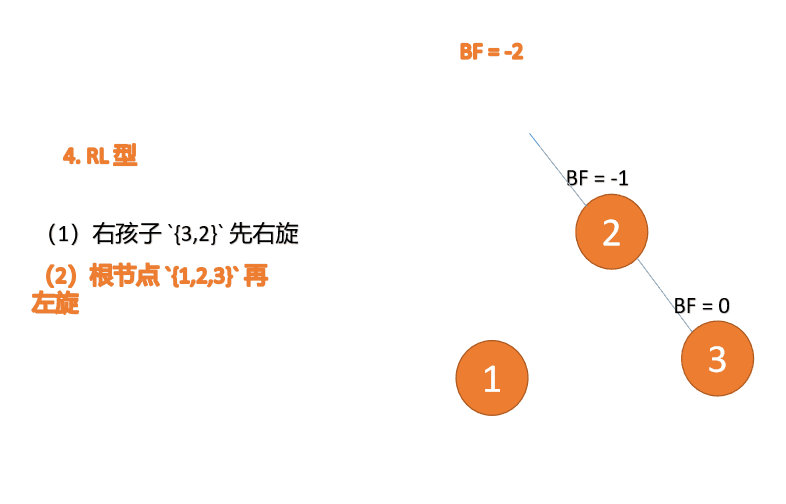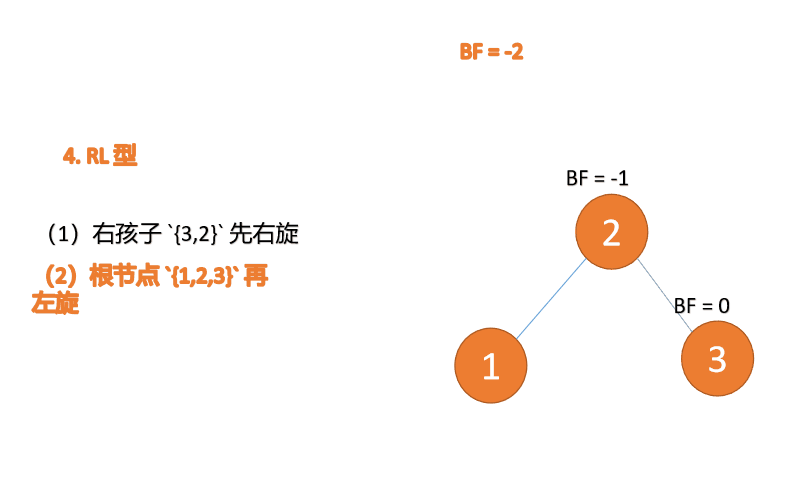 #古いルート ノード (ノード 3) は、新しいルート ノード (ノード 2) の右のサブツリーです。
#古いルート ノード (ノード 3) は、新しいルート ノード (ノード 2) の右のサブツリーです。
新しいルート ノード (ノード 2) の右のサブツリーです (ここではいいえ右のサブツリー) は古いルート ノードの左のサブツリーです。
- BF(3) = - 2 BF(4)=-1
- 、RR タイプの不均衡、最小の不均衡ツリー {3,4,5}
-
古いルート ノード (ノード 3) で左回転を実行します。新しいルート ノードです (ノード 4) の左側のサブツリーです。 新しいルート ノード (ノード 4) の左側のサブツリー (ここには左側のサブツリーはありません) は、古いノードの右側のサブツリーです。ルートノード
新しいルート ノード (ノード 4) の左側のサブツリー (ここには左側のサブツリーはありません) は、古いノードの右側のサブツリーです。ルートノード
- BF(2)=-2 BF(4)=-1
- 、 RR タイプの不均衡は最小の不均衡ツリー {1,2,4} 左回転を実行します。
-
古いルート ノード (ノード 2) は新しいルート ノード (ノード ) の左のサブツリーです。 4)
新しいルート ノード (ノード 4) 左側のサブツリー (ノード 3) は、古いルート ノードの右側のサブツリーです。
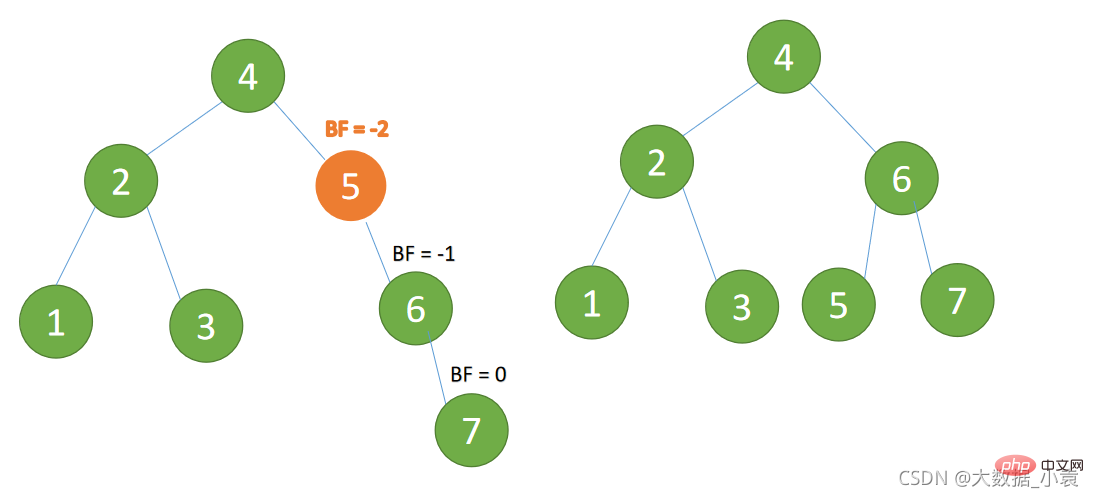
- (4) ノード 7
BF(5)=-2、BF(6)=-1 、RR 型インバランス、最小インバランス ツリーの左回りを挿入する場合
、RR 型インバランス、最小インバランス ツリーの左回りを挿入する場合 - 旧根节点(节点 5)为新根节点(节点 6)的左子树
- 新根节点的左子树(这里没有)为旧根节点的右子树
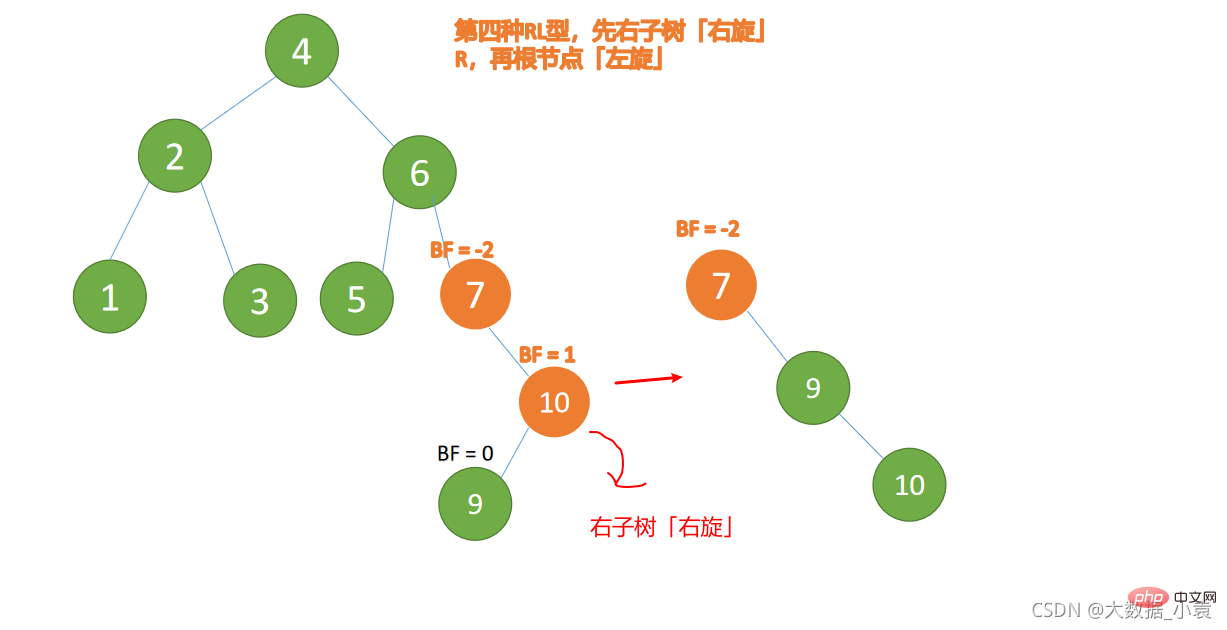
- 旧根节点(节点 10)为新根节点(节点 9)的右子树
- 新根节点(节点 9)的右子树(这里没有右子树)为旧根节点的左子树
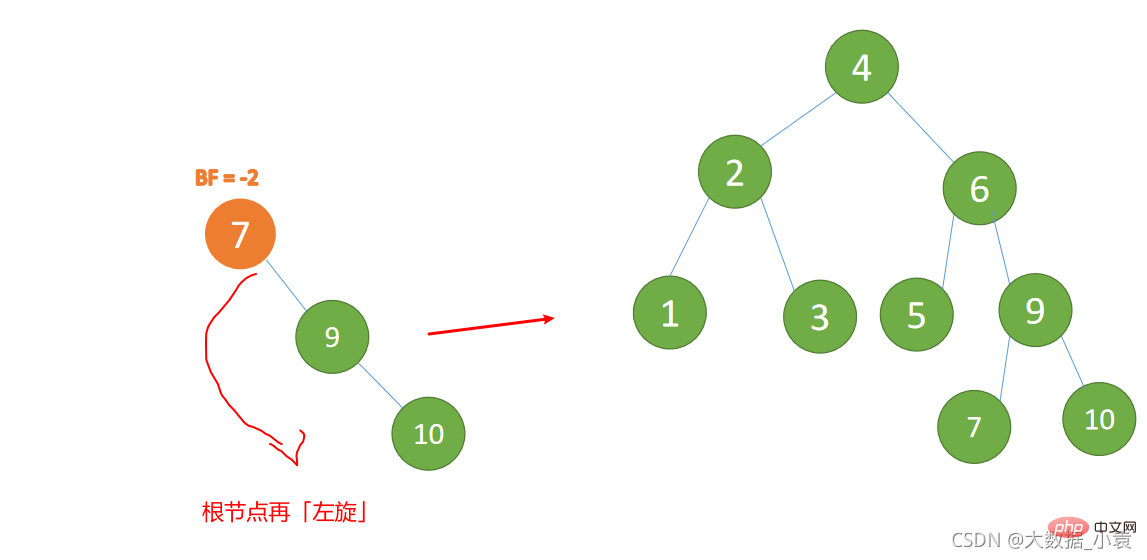
最小不平衡子树再左旋: - 旧根节点(节点 7)为新根节点(节点 9)的左子树
- 新根节点(节点 9)的左子树(这里没有左子树)为旧根节点的右子树
- 节点类
(5)依次插入 10 ,9 。插入 9 点的时候 BF(10) = 1,BF(7) = -2,RL 型失衡,对先右旋再左旋,右子树先右旋
代码实现
public class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
//获取当前节点高度
public int height() {
return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}
//获取左子树高度
public int leftHeight() {
if (left == null) {
return 0;
}
return left.height();
}
//获取右子树高度
public int rightHeight() {
if (right == null) {
return 0;
}
return right.height();
}
//向子树中添加节点
public void add(Node node) {
if (node == null) {
return;
}
/*判断传入的节点的值比当前紫薯的根节点的值大还是小*/
//添加的节点比当前节点更小(传给左节点)
if (node.value = 2) {
//双旋转,当左子树左边高度小于左子树右边高度时
if (left != null && left.leftHeight() value && this.left != null) {
return this.left.searchParent(value);
} else if (this.value
- 测试类
public class Demo {
public static void main(String[] args) {
int[] arr = {1,2,3,4,5,6};
//创建一颗二叉排序树
BinarySortTree bst = new BinarySortTree();
//循环添加
for (int i : arr) {
bst.add(new Node(i));
}
//查看高度
System.out.println(bst.root.height()); //3
//查看节点值
System.out.println(bst.root.value); //根节点为4
System.out.println(bst.root.left.value); //左子节点为2
System.out.println(bst.root.right.value); //右子节点为5
}}
第8章 赫夫曼树
8.1 赫夫曼树概述
HuffmanTree因为翻译不同所以有其他的名字:赫夫曼树、霍夫曼树、哈夫曼树
赫夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。树的路径长度是从树根到每一结点的路径长度之和,记为WPL=(W1L1+W2L2+W3L3+…+WnLn),N个权值Wi(i=1,2,…n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,…n)。可以证明赫夫曼树的WPL是最小的。
8.2 赫夫曼树定义
路径: 路径是指从一个节点到另一个节点的分支序列。
路径长度: 指从一个节点到另一个结点所经过的分支数目。 如下图:从根节点到a的分支数目为2
树的路径长度: 树中所有结点的路径长度之和为树的路径长度PL。 如下图:PL为10
节点的权: 给树的每个结点赋予一个具有某种实际意义的实数,我们称该实数为这个结点的权。如下图:7、5、2、4
带权路径长度: 从树根到某一结点的路径长度与该节点的权的乘积,叫做该结点的带权路径长度。如下图:A的带权路径长度为2*7=14
树的带权路径长度(WPL): 树的带权路径长度为树中所有叶子节点的带权路径长度之和
最优二叉树:权值最大的节点离跟节点越近的二叉树,所得WPL值最小,就是最优二叉树。如下图:(b)
- (a)
WPL=9*2+4*2+5*2+2*2=40 - (b)
WPL=9*1+5*2+4*3+2*3=37 - (c)
WPL=4*1+2*2+5*3+9*3=50
8.3 构造赫夫曼树步骤
对于数组{5,29,7,8,14,23,3,11},我们把它构造成赫夫曼树
第一步:使用数组中所有元素创建若干个二叉树,这些值作为节点的权值(只有一个节点)。
第二步:将这些节点按照权值的大小进行排序。
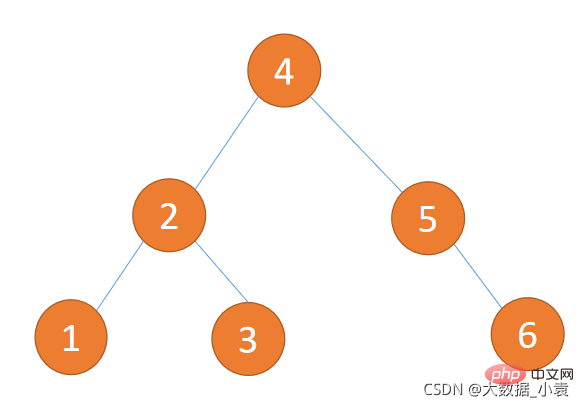
第三步:取出权值最小的两个节点,并创建一个新的节点作为这两个节点的父节点,这个父节点的权值为两个子节点的权值之和。将这两个节点分别赋给父节点的左右节点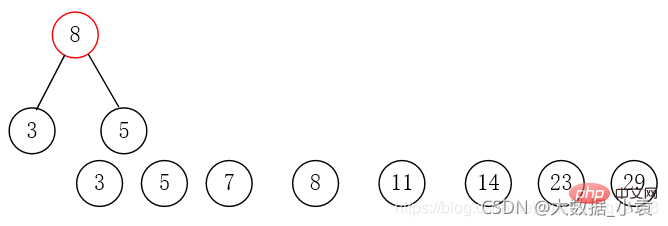
第四步:删除这两个节点,将父节点添加进集合里
第五步:重复第二步到第四步,直到集合中只剩一个元素,结束循环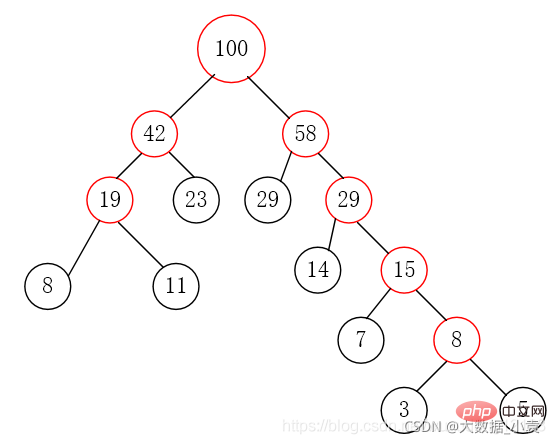
8.4 代码实现
- 节点类
//接口实现排序功能public class Node implements Comparable<node> {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
@Override
public int compareTo(Node o) {
return -(this.value - o.value); //集合倒叙,从大到小
}
@Override
public String toString() {
return "Node value=" + value ;
}}</node>
- 测试类
import java.util.ArrayList;import java.util.Collections;import java.util.List;public class Demo {
public static void main(String[] args) {
int[] arr = {5, 29, 7, 8, 14, 23, 3, 11};
Node node = createHuffmanTree(arr);
System.out.println(node); //Node value=100
}
//创建赫夫曼树
public static Node createHuffmanTree(int[] arr) {
//使用数组中所有元素创建若干个二叉树(只有一个节点)
List<node> nodes = new ArrayList();
for (int value : arr) {
nodes.add(new Node(value));
}
//循环处理
while (nodes.size() > 1) {
//排序
Collections.sort(nodes);
//取出最小的两个二叉树(集合为倒叙,从大到小)
Node left = nodes.get(nodes.size() - 1); //权值最小
Node right = nodes.get(nodes.size() - 2); //权值次小
//创建一个新的二叉树
Node parent = new Node(left.value + right.value);
//删除原来的两个节点
nodes.remove(left);
nodes.remove(right);
//新的二叉树放入原来的二叉树集合中
nodes.add(parent);
//打印结果
System.out.println(nodes);
}
return nodes.get(0);
}}</node>
- 循环次数结果
[Node value=29, Node value=23, Node value=14, Node value=11, Node value=8, Node value=7, Node value=8][Node value=29, Node value=23, Node value=14, Node value=11, Node value=8, Node value=15][Node value=29, Node value=23, Node value=15, Node value=14, Node value=19][Node value=29, Node value=23, Node value=19, Node value=29][Node value=29, Node value=29, Node value=42][Node value=42, Node value=58][Node value=100]Node value=100Process finished with exit code 0
第9章 多路查找树(2-3树、2-3-4树、B树、B+树)
9.1 为什么使用多路查找树
二叉树存在的问题
二叉树需要加载到内存的,如果二叉树的节点少,没有什么问题,但是如果二叉树的节点很多(比如1亿), 就存在如下问题:
问题1:在构建二叉树时,需要多次进行I/O操作(海量数据存在数据库或文件中),节点海量,构建二叉树时,
速度有影响.问题2:节点海量,也会造成二叉树的
高度很大,会降低操作速度.
解决上述问题 —> 多叉树
多路查找树
- 1、在二叉树中,每个节点有数据项,最多有两个子节点。如果允许每个节点可以有
更多的数据项和更多的子节点,就是多叉树(multiway tree) - 2、后面我们讲解的"2-3树","2-3-4树"就是多叉树,多叉树通过
重新组织节点,减少树的高度,能对二叉树进行优化。 - 3、举例说明(下面2-3树就是一颗多叉树)

9.2 2-3树
2-3树定义
- 所有叶子节点都要在同一层
- 二节点要么有两个子节点,要么没有节点
- 三节点要么没有节点,要么有三个子节点
- 不能出现节点不满的情况

2-3树插入的操作
插入原理:
对于2-3树的插入来说,与平衡二叉树相同,插入操作一定是发生在叶子节点上,并且节点的插入和删除都有可能导致不平衡的情况发生,在插入和删除节点时也是需要动态维持平衡的,但维持平衡的策略和AVL树是不一样的。
AVL树向下添加节点之后通过旋转来恢复平衡,而2-3树是通过节点向上分裂来维持平衡的,也就是说2-3树插入元素的过程中层级是向上增加的,因此不会导致叶子节点不在同一层级的现象发生,也就不需要旋转了。
三种插入情况:
1)对于空树,插入一个2节点即可;
2)插入节点到一个2节点的叶子上。由于本身就只有一个元素,所以只需要将其升级为3节点即可(如:插入3)。

3)插入节点到一个3节点的叶子上。因为3节点本身最大容量,因此需要拆分,且将树中两元素或者插入元素的三者中选择其一向上移动一层。
分为三种情况:
- 升级父节点(插入5)

- 升级根节点(插入11)

- 增加树高度(插入2,从下往上拆)

2-3树删除的操作
删除原理:2-3树的删除也分为三种情况,与插入相反。
三种删除情况:
1) 削除された要素は 3 ノードの葉ノードにあります。直接削除してもツリー構造には影響しません (9 個削除するなど) 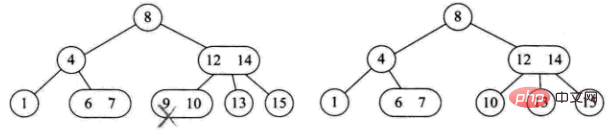
2) 削除された要素は にあります2 ノードの場合は、直接削除してツリー構造を破壊します。 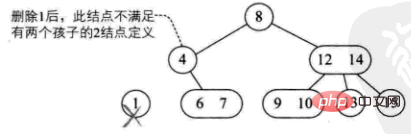
これは 4 つの状況に分けられます。
このノードの親も2 つのノードがあり、3 ノードの右の子があります (例: delete 1)

このノードの親はノード 2 で、その右の子もノード 2 です。ノード 2 (例: delete 4)

- ##このノードの親は 3 ノードです (例: delete 10)
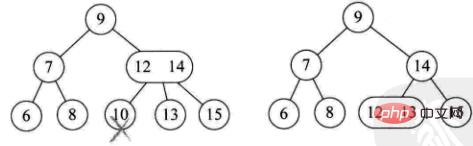
- 現在のツリーは完全なツリーです。バイナリ ツリーです。ツリーの高さを下げます (例: 8 を削除)
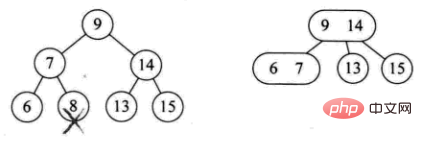
- 分岐ノードが 2 ノード (例: delete 4)
-
 分岐ノードは 3 ノードです (例: delete 12)
分岐ノードは 3 ノードです (例: delete 12) -
 ##9.3 2-3- 4 ツリー
##9.3 2-3- 4 ツリー
2 -3-4 ツリーは、4 つのノードの使用を含む 2-3 ツリーの拡張です。4 ノードには、小、中、大の 3 つの要素と 4 つの子が含まれます (または子がありません)。 )
2-3-4 ツリー挿入操作
1) 挿入するノードが 4 ノードでない場合は直接挿入してください
2) ノードが 4 つでない場合は、直接挿入してください。挿入するノードは 4 ノードで、最初に新しいノードを一時的に挿入して 5 ノードになり、次に 5 ノードを上に分割してマージします。5 ノードは 2 つの 2 ノードに分割されます (5 ノードの最小要素、2 番目の要素) 5 ノードの 1 つ)、および 1 つの 3 ノード (5 ノードの後の 2 つの要素) )、上向きに分割した後の 2 番目の 2 ノードを親ノードにマージし、挿入後の親ノードを現在のノードとして使用します。要素に対して、2-3-4 ツリーの要件が満たされるまで手順 (1) と (2) を繰り返します。 プロパティを定義します。
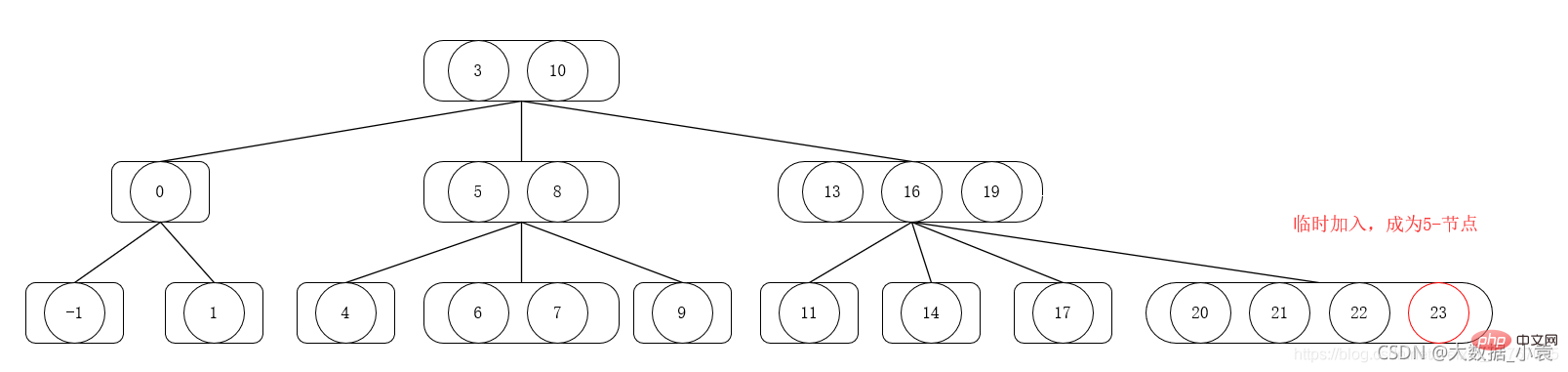

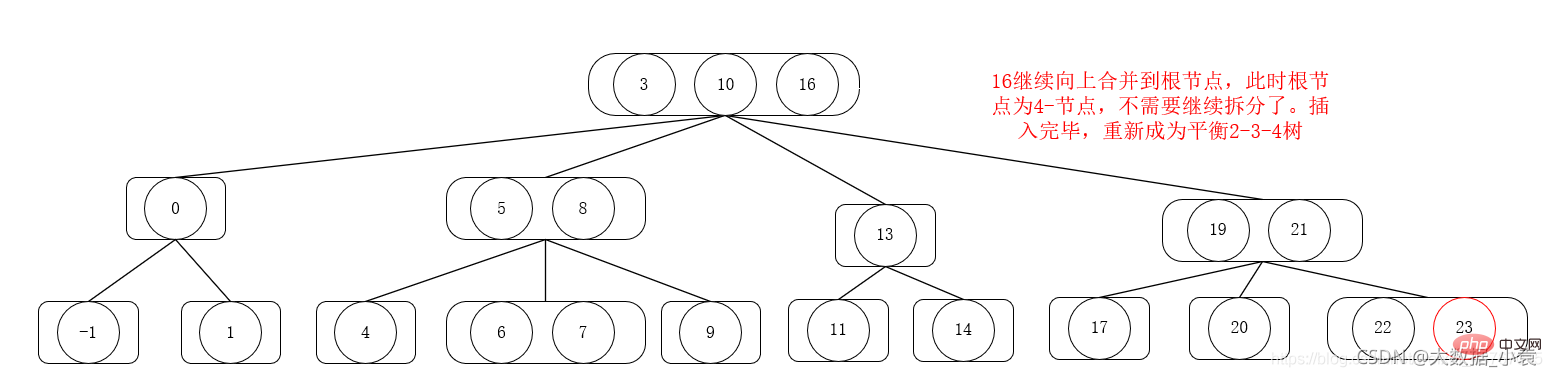 2-3-4 ツリー削除操作
2-3-4 ツリー削除操作
削除順序は 1,6,3,4,5,2,9
 9.4 B-tree
9.4 B-tree
B ツリー (BTree) はバランスのとれたマルチパス検索ツリーであり、2-3 ツリーと 2-3-4 ツリーはすべて B ツリーの特殊なケースです。
最大のノードを持つ子ツリーを B ツリーの次数と呼びます。したがって、2-3 ツリーは 3 次の B ツリーであり、2-3-4 ツリーは 4 次の B ツリーです。 -order B-tree
 以下に示すように、例えば 7 を求めるには、まずルートノードの 3、5、8 の 3 つの要素を外部メモリから読み出します。 7 は存在せず、5 と 8 の間にあることがわかったので、A2 を検索し、ノード 2、6、7 を外部メモリから読み出し、最後を見つけます。
以下に示すように、例えば 7 を求めるには、まずルートノードの 3、5、8 の 3 つの要素を外部メモリから読み出します。 7 は存在せず、5 と 8 の間にあることがわかったので、A2 を検索し、ノード 2、6、7 を外部メモリから読み出し、最後を見つけます。

。処理するデータが大きい場合、一度にメモリにロードすることができません。このとき、Bツリーの順序がハードディスクに格納されているページサイズと一致するようにBツリーが調整される。たとえば、B ツリーの次数は 1001 (つまり、1 ノードに 1000 個のキーワードが含まれる)、高さは 2 (0 から始まる) であり、10 億を超えるキーワード (1001x1001x1000 1001x1000 1000) を保存できます。ルート ノード メモリ内に永続化されている場合、このツリー内で特定のキーワードを検索するには、最大 2 回のハードディスク読み取りが必要です。 n 個のキーワードを持つ m 次の B ツリーの場合、最悪の場合の検索時間の計算 n 個のキーワードを含む B ツリーを検索する場合、ルート ノードからキーワード ノードまでのパスに含まれるノードの数はそれほど多くありません。 B-treeはB-treeのバージョンアップ版とも言え、B-treeに比べてノードを最大限に活用します。スペースが確保され、クエリ速度がより安定し、二分探索に完全に近い速度になります。ほとんどのファイル システムとデータは、B ツリーを使用してインデックス構造を実装します。 葉以外のノードに n 個のキーワードが含まれる n 個のサブツリーがあります (B ツリーでは n-1 個のキーワード)。ただし、各キーワードはデータを保存するのではなく、同じキーワードのインデックスをリーフ ノードに保存するためにのみ使用され、すべてのデータはリーフ ノードに保存されます。 (ここで、非リーフノードの m 個のサブツリーと n 個のキーワードの関係について、mysql のインデックス構造は上記の m=n ではなく、m=n 1 のようです) B ツリーのすべてのリーフ ノードは順序付きリンク リストを形成し、リーフ ノードをトラバースすることによってのみツリー全体をトラバースできます。データの範囲クエリには便利ですが、B-tree ではそのような操作がサポートされていないか、非効率すぎます。 最新のデータベースおよびファイル システムのインデックス テーブルのほとんどは B ツリーを使用して実装されていますが、すべてではありません 第 10 章 図の構造 无向图: 若顶点 Vi 到 Vj 之间的边没有方向,则称这条边为无向边 (Edge) ,用无序偶对 (Vi,Vj) 来表示。如果图中任意两个顶点之间的边都是无向边,则称该图为无向图 (Undirected graphs)。 如:下图就是一个无向图,由于是无方向的,连接顶点 A 与 D 的边,可以表示无序队列(A,D),也可以写成 (D,A),但不能重复。顶点集合 有向图: 用有序偶 如:下图就是一个有向图。连接顶点 A 到 D 的有向边就是弧,A是弧尾,D 是弧头, 表示弧, 注意不能写成 有权图: 有些图的边或弧具有与它相关的数字,这种与图的边或弧相关的数叫做权 (Weight) 。这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网 (Network)。 如下图 图结构的常见的两个存储方式: 邻接矩阵 、邻接表 先来看第一行,该行对应的是顶点A,那我们就拿顶点A与其它点一一对应,发现顶点A除了不能通向顶点D和自身,可以通向其它任何一个的顶点 因为该图为无向图,因此顶点A如果能通向另一个顶点,那么这个顶点也一定能通向顶点A,所以这个顶点对应顶点A的也应该是 1 虽然我们确实用邻接矩阵表示了图结构,但是它有一个致命的缺点,那就是矩阵中存在着大量的 0,这在程序中会占据大量的内存。此时我们思考一下,0 就是表示没有,没有为什么还要写,所以我们来看一下第二种表示图结构的方法,它就很好的解决了邻接矩阵的缺陷 代码实现: 邻接表 是由每个顶点以及它的相邻顶点组成的 如上图:图中最左侧红色的表示各个顶点,它们对应的那一行存储着与它相关联的顶点 从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次,这一过程就叫做图的遍历 在图结构中,存在着两种遍历搜索的方式,分别是 广度优先搜索 和 深度优先搜索 广度优先遍历(BFS):类似于图的层次遍历,它的基本思想是:首先访问起始顶点v,然后选取v的所有邻接点进行访问,再依次对v的邻接点相邻接的所有点进行访问,以此类推,直到所有顶点都被访问过为止 BFS和树的层次遍历一样,采取队列实现,这里添加一个标记数组,用来标记遍历过的顶点 执行步骤: 代码实现: 深度优先遍历(DFS):从一个顶点开始,沿着一条路径一直搜索,直到到达该路径的最后一个结点,然后回退到之前经过但未搜索过的路径继续搜索,直到所有路径和结点都被搜索完毕 DFS与二叉树的先序遍历类似,可以采用递归或者栈的方式实现 执行步骤: 代码实现: 冒泡排序(Bubble Sort)是一种简单的排序算法。它重复地遍历要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。 运行流程: 动图实现: 交换过程图示(第一次): 排序分析:待排数组中一共有6个数,第一轮排序时进行了5次比较,第二轮排序时进行了4比较,依次类推,最后一轮进行了1次比较。 数组元素总数为N时,则一共需要的比较次数为: 算法约做了 交换和比较的操作次数都与 N^2 成正比,由于在大O表示法中,常数忽略不计,冒泡排序的时间复杂度为 O(N2)的时间复杂度是一个比较糟糕的结果,尤其在数据量很大的情况下。所以冒泡排序通常不会用于实际应用。 传统的冒泡算法每次排序只确定了最大值,我们可以在每次循环之中进行正反两次冒泡,分别找到最大值和最小值,如此可使排序的轮数减少一半 选择排序与冒泡排序一样,需要进行 虽然选择排序与冒泡排序在时间复杂度属于同一量级,但是毫无疑问选择排序的效率更高,因为它的交换操作次数更少,而且在交换操作比比较操作的时间级大得多时,选择排序的速度是相当快的。 传统的选择排序每次只确定最小值,根据改进冒泡算法的经验,我们可以对排序算法进行如下改进:每趟排序确定两个最值——最大值与最小值,这样就可以将排序趟数缩减一半 改进后代码如下: 插入排序(Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间 动图展示: 在第一趟排序中,插入排序最多比较一次,第二趟最多比较两次,依次类推,最后一趟最多比较N-1次。因此有: 因为在每趟排序发现插入点之前,平均来说,只有全体数据项的一半进行比较,我们除以2得到: 复制的次数大致等于比较的次数,然而,一次复制与一次比较的时间消耗不同,所以相对于随机数据,这个算法比冒泡排序快一倍,比选择排序略快。 与冒泡排序、选择排序一样,插入排序的时间复杂度仍然为 如果待排序数组基本有序时,插入排序的效率会更高 在插入某个元素之前需要先确定该元素在有序数组中的位置,上例的做法是对有序数组中的元素逐个扫描,当数据量比较大的时候,这是一个很耗时间的过程,可以采用二分查找法改进,这种排序也被称为二分插入排序 归并排序(Merge Sort)是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组,再合并数组。 将数组分解最小之后,然后合并两个有序数组,基本思路是比较两个数组的最前面的数,谁小就先取谁,取了后相应的指针就往后移一位。然后再比较,直至一个数组为空,最后把另一个数组的剩余部分复制过来即可。 动图展示: 递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。 动图展示: 从一开始快速排序平均需要花费O(n log n)时间的描述并不明显。但是不难观察到的是分区运算,数组的元素都会在每次循环中走访过一次,使用O(n)的时间。在使用结合(concatenation)的版本中,这项运算也是O(n)。 在最好的情况,每次我们运行一次分区,我们会把一个数列分为两个几近相等的片段。这个意思就是每次递归调用处理一半大小的数列。因此,在到达大小为一的数列前,我们只要作log n次嵌套的调用。这个意思就是调用树的深度是O(log n)。但是在同一层次结构的两个程序调用中,不会处理到原来数列的相同部分;因此,程序调用的每一层次结构总共全部仅需要O(n)的时间(每个调用有某些共同的额外耗费,但是因为在每一层次结构仅仅只有O(n)个调用,这些被归纳在O(n)系数中)。结果是这个算法仅需使用O(n log n)时间。 希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL.Shell于1959年提出而得名。 希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止 动图展示: 静图分析: 希尔排序不像其他时间复杂度为O(N log2N)的排序算法那么快,但是比选择排序和插入排序这种时间复杂度为O(N2)的排序算法还是要快得多,而且非常容易实现。它在最坏情况下的执行效率和在平均情况下的执行效率相比不会降低多少,而快速排序除非采取特殊措施,否则在最坏情况下的执行效率变得非常差。 迄今为止,还无法从理论上精准地分析希尔排序的效率,有各种各样基于试验的评估,估计它的时间级介于O(N^3/2)与 O(N^7/6)之间。我们可以认为希尔排序的平均时间复杂度为 堆排序(Heap Sort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图: 大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] 小顶堆:arr[i] 步骤一 构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆) 1)假设给定无序序列结构如下 步骤二 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换 1)将堆顶元素9和末尾元素4进行交换,9就不用继续排序了 排序思路: 将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆; 将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端; 重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序 动图展示: 它的运行时间主要是消耗在初始构建堆和在重建堆时的反复筛选上。 在构建堆的过程中,因为我们是完全二叉树从最下层最右边的非终端结点开始构建,将它与其孩子进行比较和若有必要的互换,对于每个非终端结点来说,其实最多进行两次比较和互换操作,因此整个构建堆的时间复杂度为O(n)。 在正式排序时,第i次取堆顶记录重建堆需要用O(logi)的时间(完全二叉树的某个结点到根结点的距离为log2i+1),并且需要取n-1次堆顶记录,因此,重建堆的时间复杂度为 所以总体来说,堆排序的时间复杂度为O(nlogn)。由于堆排序对原始记录的排序状态并不敏感,因此它无论是最好、最坏和平均时间复杂度均为O(nlogn)。这在性能上显然要远远好过于冒泡、简单选择、直接插入的O(n2)的时间复杂度了。 空间复杂度上,它只有一个用来交换的暂存单元,也非常的不错。不过由于记录的比较与交换是跳跃式进行,因此堆排序是一种不稳定的排序方法。 计数排序(Counting Sort)不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。 排序步骤: 动图展示: 计数排序是一个稳定的排序算法。当输入的元素是 n 个 0到 k 之间的整数时,时间复杂度是 桶排序 (Bucket sort)或所谓的箱排序,是一个排序算法,工作的原理是将数组分到有限数量的桶里。每个桶再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序),最后依次把各个桶中的记录列出来记得到有序序列。桶排序是鸽巢排序的一种归纳结果。当要被排序的数组内的数值是均匀分配的时候,桶排序使用线性时间 排序步骤: 动图展示: 静图展示: 初看起来,基数排序的执行效率似乎好的让人无法相信,所有要做的只是把原始数据项从数组复制到链表,然后再复制回去。如果有10个数据项,则有20次复制,对每一位重复一次这个过程。假设对5位的数字排序,就需要20 * 5=100次复制。 *如果有100个数据项,那么就有200 * 5=1000次复制。复制的次数与数据项的个数成正比,即O(n)。这是我们看到的效率最高的排序算法。 不幸的是,数据项越多,就需要更长的关键字,如果数据项增加10倍,那么关键字必须增加一位(多一轮排序)。复制的次数和数据项的个数与关键字长度成正比,可以认为关键字长度是N的对数。因此在大多数情况下,基数排序的执行效率倒退为O(N*logN),和快速排序差不多 推荐学习:《java教程》
最初のレベルに少なくとも 1 つのノード、2 番目のレベルに少なくとも 2 つのノードが必要です。ルート ノードを除くすべてのノードには、各ブランチ ノードに少なくとも ⌈m/2⌉ のサブツリーがあるため、第 3 レベルには少なくとも 2x⌈m/2⌉ のノードがあります。 。 。このように、k 1 層には少なくとも 2x(⌈m/2⌉)^(k-1) があり、実際には、k 1 層のノードはリーフ ノードです。 m 次の B ツリーに n 個のキーワードがある場合、リーフ ノードが見つかったとき、それは実際には失敗したノードが n 1 であることを意味するため、
n 1>=2x(⌈m/2⌉)^(k -1)、つまり 

9.5 B-tree
以下の図の B ツリーをトラバースする必要があります。各ノードがハードディスク上の異なるページに属していると仮定します。すべての要素を、ページ 2-ページ 1-ページ 3 の順序でトラバースします。 - ページ 1 ~ ページ 4。 - ページ 1 - ページ 5、ページ 1 は 3 回走査されており、ノードを走査するたびに、ノード内の要素を 1 回走査します。 ##B ツリーはファイル システムです。B ツリーを変形したツリーです。B ツリーでは、各要素はツリー内に 1 回だけ出現します。B ツリーでは、ブランチ ノードに出現する要素は次のようになります。分岐ノード内の順序どおりの位置とみなされ、後続ノード (葉ノード) に再度リストされます。さらに、各リーフ ノードは次のリーフ ノードへのポインタを保存します。
下の図は B ツリーです。灰色のキーワードがルート ノードに表示され、リーフ ノードに再びリストされます。
次数 m の B ツリーB ツリーの違いは  :
: #すべてのリーフ ノードには、すべてのキーワードに関する情報と、これらのキーワードが指す特定のディスク レコードへのポインタ データが含まれており、各リーフ ノードには、次に隣接するリーフ ノードへのポインタがあります。
B ツリーのクエリ効率は安定していません。最良の場合、クエリは 1 回 (ルート ノード) のみですが、最悪の場合、リーフ ノードが見つかります。ただし、B ツリーにはデータ アドレスは保存されず、リーフ ノードのキーのインデックスのみが保存されます。すべてのクエリは、ヒットとみなされるリーフ ノードを見つける必要があり、クエリ効率は比較的安定しています。これは、SQL ステートメントを最適化するのに非常に役立ちます。
一般的に使用される用語:
#用語
意味
##頂点
グラフ ノード内の誰か
エッジ
頂点間の接続
隣接する頂点
は同じ頂点によって接続されていますエッジによって接続されています
次数
頂点の隣接する頂点の数
単純なパス #ループ 1 つの頂点からのルート頂点を経由せずに別の頂点へ繰り返し
#開始点と終了点は同じ頂点
無向グラフ グラフ内のすべてのエッジには方向がありません
有向グラフ グラフ内のすべてのエッジには方向があります
重み付けされていないグラフ グラフのエッジには重み値がありません
重み付けされたグラフ グラフには特定の重み値があります
图的结构很简单,就是由顶点 V 集和边 E 集构成,因此图可以表示成 G = (V,E)V = {A,B,C,D};边集合 E = {(A,B),(A,D),(A,C)(B,C),(C,D),}
V = { A,B,C,D}; 弧集合 E = {<a>,<b>,<b>,<c>}</c></b></b></a>
注意:无向边用小括号 “()” 表示,而有向边则是用尖括号""表示
10.2 图的存储结构及实现
邻接矩阵
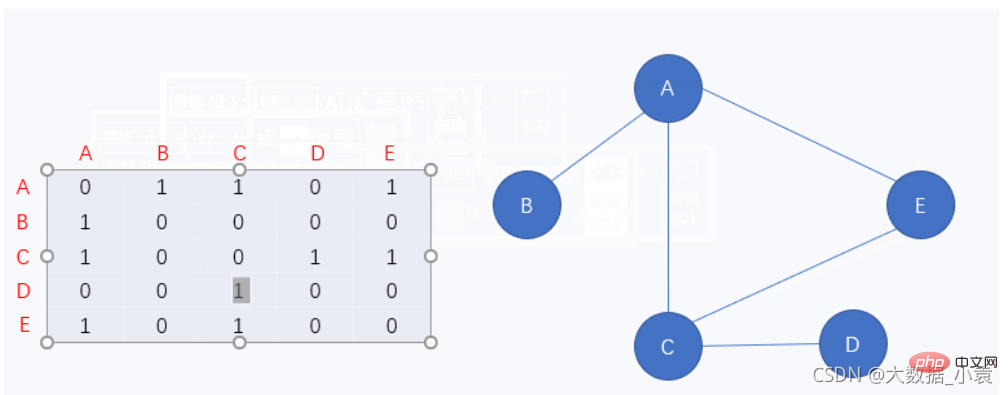 图中的 0 表示该顶点无法通向另一个顶点,相反 1 就表示该顶点能通向另一个顶点
图中的 0 表示该顶点无法通向另一个顶点,相反 1 就表示该顶点能通向另一个顶点public class Vertex {
private String value;
public Vertex(String value) {
this.value = value;
}
public String getValue() {
return value;
}
public void setValue(String value) {
this.value = value;
}
@Override
public String toString() {
return value;
}}
public class Graph {
private Vertex[] vertex; //顶点数组
private int currentSize; //默认顶点位置
public int[][] adjMat; //邻接表
public Graph(int size) {
vertex = new Vertex[size];
adjMat = new int[size][size];
}
//向图中加入顶点
public void addVertex(Vertex v) {
vertex[currentSize++] = v;
}
//添加边
public void addEdge(String v1, String v2) {
//找出两个点的下标
int index1 = 0;
for (int i = 0; i
public class Demo {
public static void main(String[] args) {
Vertex v1 = new Vertex("A");
Vertex v2 = new Vertex("B");
Vertex v3 = new Vertex("C");
Vertex v4 = new Vertex("D");
Vertex v5 = new Vertex("E");
Graph g = new Graph(5);
g.addVertex(v1);
g.addVertex(v2);
g.addVertex(v3);
g.addVertex(v4);
g.addVertex(v5);
//增加边
g.addEdge("A", "B");
g.addEdge("A", "C");
g.addEdge("A", "E");
g.addEdge("C", "E");
g.addEdge("C", "D");
for (int[] a : g.adjMat) {
System.out.println(Arrays.toString(a));
}
}}
[0, 1, 1, 0, 1][1, 0, 0, 0, 0][1, 0, 0, 1, 1][0, 0, 1, 0, 0][1, 0, 1, 0, 0]
邻接表

顶点A 与 顶点B 、顶点C 、顶点E 相关联顶点B 与 顶点A 相关联顶点C 与 顶点A 、顶点D 、顶点E 相关联顶点D 与 顶点C 相关联顶点E 与 顶点A 、顶点C 相关联10.3 图的遍历方式及实现
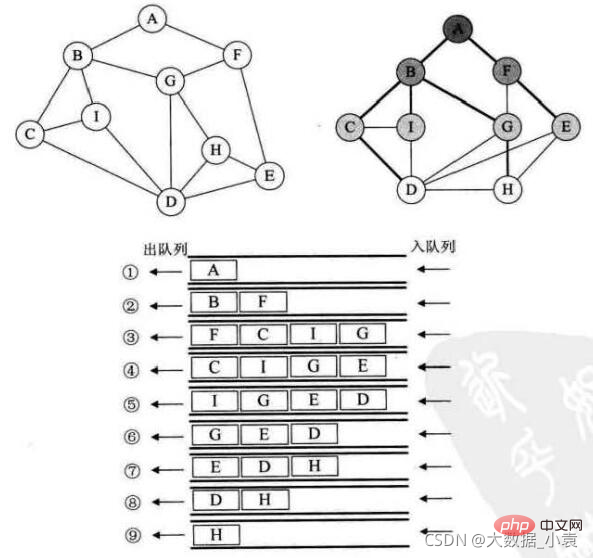
广度优先搜索
深度优先搜索

1 -> 2 -> 3 -> 6 -> 9 -> 8 -> 5 -> 4
8 -> 7
7 -> 8 -> 9 -> 6 -> 3 -> 2 -> 1,流程结束public class MyStack {
//栈的底层使用数组来存储数据
//private int[] elements;
int[] elements; //测试时使用
public MyStack() {
elements = new int[0];
}
//添加元素
public void push(int element) {
//创建一个新的数组
int[] newArr = new int[elements.length + 1];
//把原数组中的元素复制到新数组中
for (int i = 0; i
public class Vertex {
private String value;
public boolean visited; //访问状态
public Vertex(String value) {
super();
this.value = value;
}
public String getValue() {
return value;
}
public void setValue(String value) {
this.value = value;
}
@Override
public String toString() {
return value;
}}
import mystack.MyStack;public class Graph {
private Vertex[] vertex; //顶点数组
private int currentSize; //默认顶点位置
public int[][] adjMat; //邻接表
private MyStack stack = new MyStack(); //栈
private int currentIndex; //当前遍历的下标
public Graph(int size) {
vertex = new Vertex[size];
adjMat = new int[size][size];
}
//向图中加入顶点
public void addVertex(Vertex v) {
vertex[currentSize++] = v;
}
//添加边
public void addEdge(String v1, String v2) {
//找出两个点的下标
int index1 = 0;
for (int i = 0; i
import java.util.Arrays;public class Demo {
public static void main(String[] args) {
Vertex v1 = new Vertex("A");
Vertex v2 = new Vertex("B");
Vertex v3 = new Vertex("C");
Vertex v4 = new Vertex("D");
Vertex v5 = new Vertex("E");
Graph g = new Graph(5);
g.addVertex(v1);
g.addVertex(v2);
g.addVertex(v3);
g.addVertex(v4);
g.addVertex(v5);
//增加边
g.addEdge("A", "B");
g.addEdge("A", "C");
g.addEdge("A", "E");
g.addEdge("C", "E");
g.addEdge("C", "D");
for (int[] a : g.adjMat) {
System.out.println(Arrays.toString(a));
}
//深度优先遍历
g.dfs();// A// B// C// E// D
}}
第11章 冒泡排序(含改进版)
11.1 冒泡排序概念
静图详解: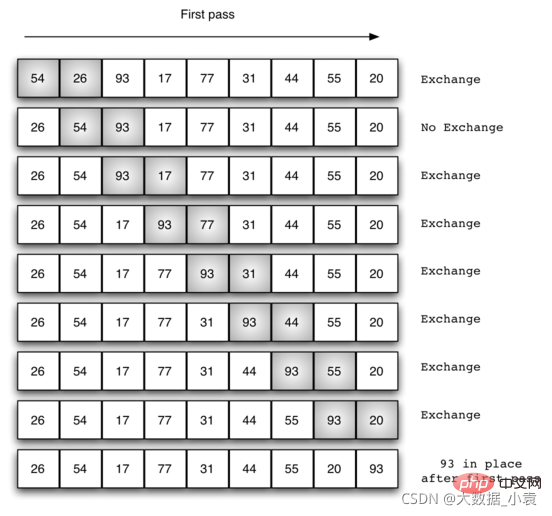 那么我们需要进行n-1次冒泡过程,每次对应的比较次数如下图所示:
那么我们需要进行n-1次冒泡过程,每次对应的比较次数如下图所示: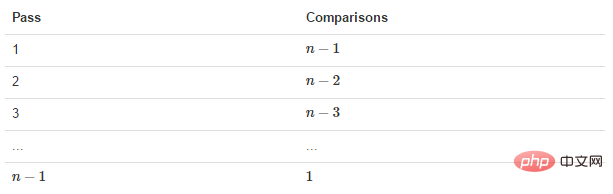
11.2 代码实现
import java.util.Arrays;public class BubbleSort {
public static void main(String[] args) {
int[] arr = {4, 5, 6, 3, 2, 1};
bubbleSort(arr);// [4, 5, 3, 2, 1, 6]// [4, 3, 2, 1, 5, 6]// [3, 2, 1, 4, 5, 6]// [2, 1, 3, 4, 5, 6]// [1, 2, 3, 4, 5, 6]
}
//冒泡排序,共需要比较length-1轮
public static void bubbleSort(int[] arr) {
//控制一共比较多少轮
for (int i = 0; i arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
//打印每次排序后的结果
System.out.println(Arrays.toString(arr));
}
}}
11.3 时间复杂度
O(n) (表示遍历一次发现没有任何可以交换的元素,排序结束。)O(n^2)
(N-1)+ (N-2)+ (N-3)+ ...1=N*(N-1)/2N^2/2次比较。因为只有在前面的元素比后面的元素大时才交换数据,所以交换的次数少于比较的次数。如果数据是随机的,大概有一半数据需要交换,则交换的次数为N^2/4(不过在最坏情况下,即初始数据逆序时,每次比较都需要交换)。O(N^2)。11.4 代码改进
import java.util.Arrays;public class BubbleSort {
public static void main(String[] args) {
int[] arr = {4, 5, 6, 3, 2, 1};
bubbleSort(arr);// [1, 4, 5, 3, 2, 6]// [1, 2, 4, 3, 5, 6]// [1, 2, 3, 4, 5, 6]
}
//冒泡排序改进
public static void bubbleSort(int[] arr) {
int left = 0;
int right = arr.length - 1;
while (left arr[i + 1]) {
int temp = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = temp;
}
}
--right;
//反向冒泡,确定最小值
for (int j = right; j > left; --j) {
//如果前一位大于后一位,交换位置
if (arr[j] <h2>第12章 选择排序(含改进版)</h2><h2>12.1 选择排序概念</h2><p><strong>选择排序</strong>(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。</p><p>选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上,则它不会被移动。选择排序每次交换一对元素,它们当中至少有一个将被移到其最终位置上,因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中,选择排序属于非常好的一种</p><p><strong>动图展示</strong>:</p><p>动图1:<br><img src="https://img.php.cn/upload/article/000/000/067/3b7ad076c398e7fcf7a71a090a7e1fee-89.gif" alt="Javaのデータ構造とアルゴリズムの詳細な図解説明"><br> 动图2:<br><img src="https://img.php.cn/upload/article/000/000/067/4aef1844623c7df749806b371054cd1f-90.gif" alt="Javaのデータ構造とアルゴリズムの詳細な図解説明"></p><h2>12.2 代码实现</h2><pre class="brush:php;toolbar:false">import java.util.Arrays;public class seletsort {
public static void main(String[] args) {
int[] arr = {4, 5, 6, 3, 2, 1};
selectSort(arr);// [1, 5, 6, 3, 2, 4]// [1, 2, 6, 3, 5, 4]// [1, 2, 3, 6, 5, 4]// [1, 2, 3, 4, 5, 6]// [1, 2, 3, 4, 5, 6]// [1, 2, 3, 4, 5, 6]
}
//选择排序
public static void selectSort(int[] arr) {
//遍历所有的数
for (int i = 0; i arr[j]) {
//记录最小的那个数的下标
minIndex = j;
}
}
//如果发现了更小的元素,与第一个元素交换位置(第一个不是最小的元素)
if (i != minIndex) {
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
//打印每次排序后的结果
System.out.println(Arrays.toString(arr));
}
}}12.3 时间复杂度
O(n^2)
O(n^2)
N*(N-1)/2次比较,但是只需要N次交换,当N很大时,交换次数的时间影响力更大,所以选择排序的时间复杂度为O(N^2)。12.4 代码改进
import java.util.Arrays;public class seletsort {
public static void main(String[] args) {
int[] arr = {4, 5, 6, 3, 2, 1};
selectSort(arr);// [1, 5, 4, 3, 2, 6]// [1, 2, 4, 3, 5, 6]// [1, 2, 3, 4, 5, 6]
}
//选择排序改进
public static void selectSort(int[] arr) {
int minIndex; // 存储最小元素的小标
int maxIndex; // 存储最大元素的小标
for (int i = 0; i arr[maxIndex]) {
maxIndex = j;
}
}
//如果发现了更小的元素,与第一个元素交换位置(第一个不是最小的元素)
if (i != minIndex) {
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
// 原来的第一个元素已经与下标为minIndex的元素交换了位置
// 所以现在arr[minIndex]存放的才是之前第一个元素中的数据
// 如果之前maxIndex指向的是第一个元素,那么需要将maxIndex重新指向arr[minIndex]
if (maxIndex == i) {
maxIndex = minIndex;
}
}
// 如果发现了更大的元素,与最后一个元素交换位置
if (arr.length - 1 - i != maxIndex) {
int temp = arr[arr.length - 1 - i];
arr[arr.length - 1 - i] = arr[maxIndex];
arr[maxIndex] = temp;
}
System.out.println(Arrays.toString(arr));
}
}}
第13章 插入排序(含改进版)
13.1 插入排序概念
13.2 代码实现
import java.util.Arrays;public class InsertSort {
public static void main(String[] args) {
int[] arr = {4, 5, 6, 3, 2, 1};
insertSort(arr);// [4, 5, 6, 3, 2, 1]// [4, 5, 6, 3, 2, 1]// [3, 4, 5, 6, 2, 1]// [2, 3, 4, 5, 6, 1]// [1, 2, 3, 4, 5, 6]
}
//插入排序
public static void insertSort(int[] arr) {
//遍历所有的数字,从第二个开始和前一个比较
for (int i = 1; i = 0 && temp <h2>13.3 时间复杂度</h2>
O(n) (升序排列,序列已经处于升序状态)O(n^2)
1+2+3+...+N-1 = N*N(N-1)/2N*N(N-1)/4O(N^2),这三者被称为简单排序或者基本排序,三者都是稳定的排序算法。13.4 代码改进
import java.util.Arrays;public class InsertSort {
public static void main(String[] args) {
int[] arr = {4, 5, 6, 3, 2, 1};
insertSort(arr);// [4, 5, 6, 3, 2, 1]// [4, 5, 6, 3, 2, 1]// [3, 4, 5, 6, 2, 1]// [2, 3, 4, 5, 6, 1]// [1, 2, 3, 4, 5, 6]
}
//二分插入排序
public static void insertSort(int[] arr) {
for (int i = 1; i left; j--) {
arr[j] = arr[j - 1];
}
arr[left] = temp;
}
System.out.println(Arrays.toString(arr));
}
}}
第14章 归并排序
14.1 归并排序概念
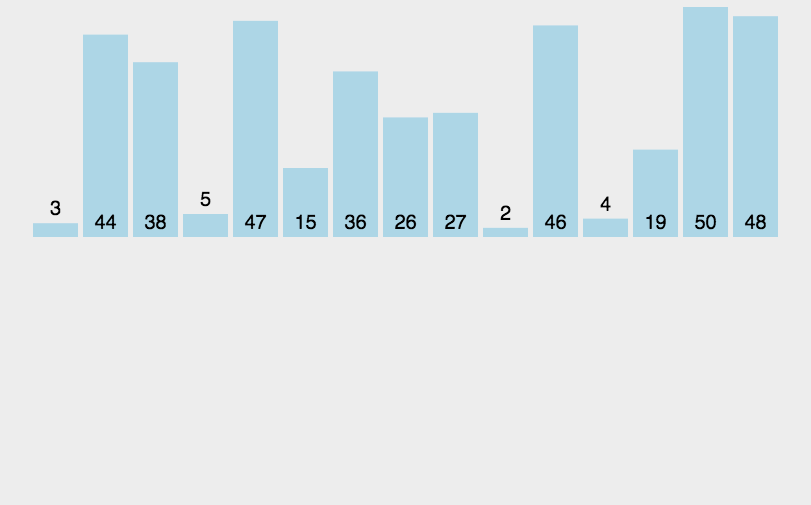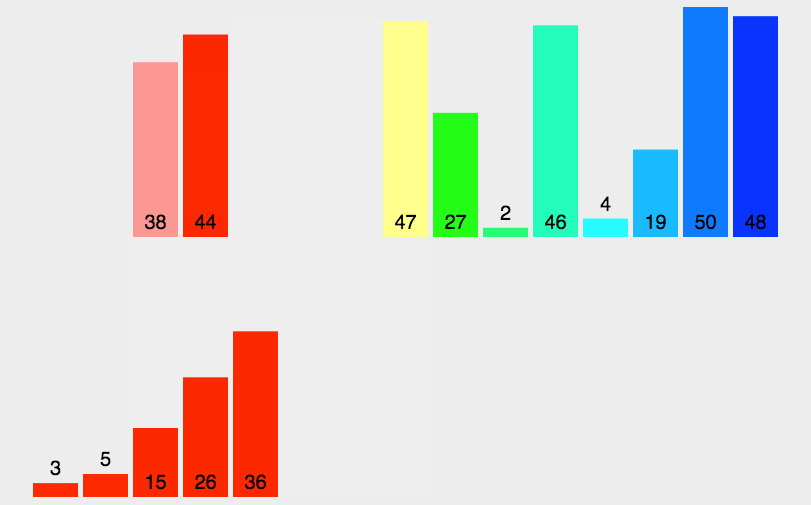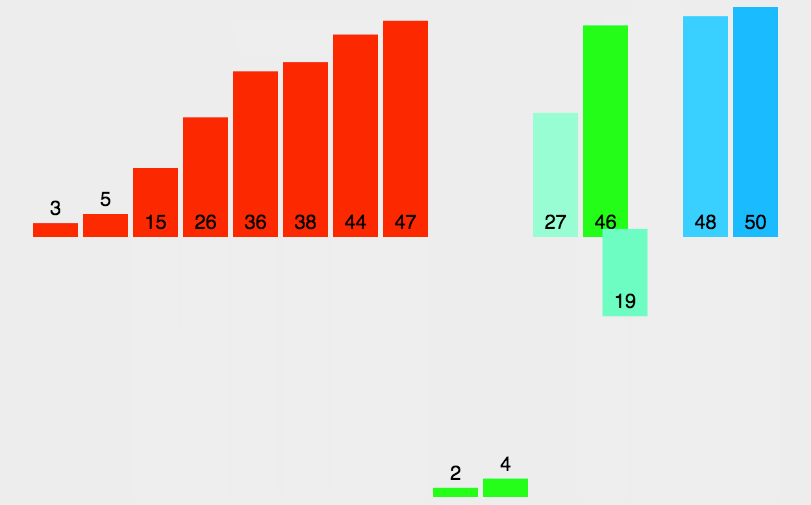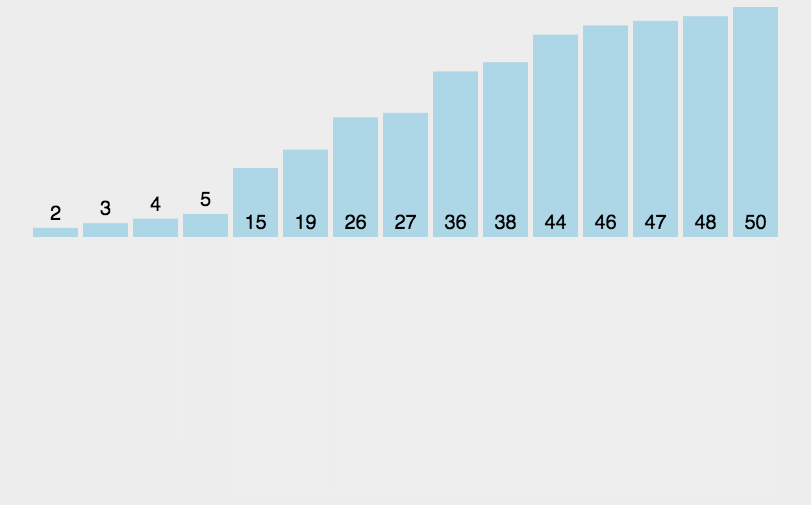
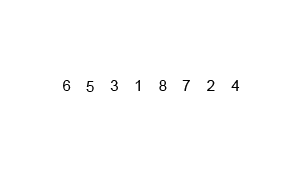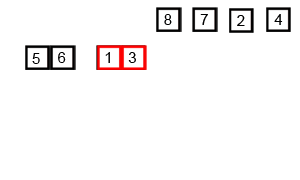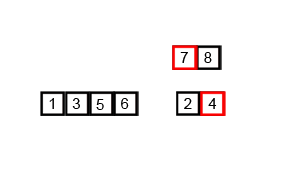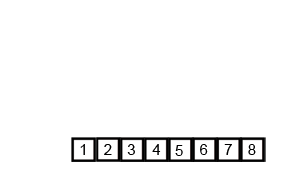
14.2 代码实现
import java.util.Arrays;public class MergeSort {
public static void main(String[] args) {
int[] arr = {6, 5, 3, 1, 8, 7, 2, 4};
mergeSort(arr, 0, arr.length - 1);// [5, 6, 3, 1, 8, 7, 2, 4]// [5, 6, 1, 3, 8, 7, 2, 4]// [1, 3, 5, 6, 8, 7, 2, 4]// [1, 3, 5, 6, 7, 8, 2, 4]// [1, 3, 5, 6, 7, 8, 2, 4]// [1, 3, 5, 6, 2, 4, 7, 8]// [1, 2, 3, 4, 5, 6, 7, 8]
}
//归并排序
public static void mergeSort(int[] arr, int low, int high) {
int middle = (high + low) / 2;
//递归结束
if (low <h2>14.3 时间复杂度</h2><p>最优时间复杂度:<code>O(nlogn)</code></p><p>最坏时间复杂度:<code>O(nlogn)</code></p><p>稳定性:稳定</p><h2>第15章 快速排序</h2><h2>15.1 快速排序概念</h2><p><strong>快速排序</strong>(Quick Sort),又称划分交换排序(partition-exchange sort),通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。</p><p><strong>排序步骤</strong>:</p>

静图分析:
15.2 代码实现
import java.util.Arrays;public class QuickSort {
public static void main(String[] args) {
int[] arr = {30, 40, 60, 10, 20, 50};
quickSort(arr, 0, arr.length - 1);// [20, 10, 30, 60, 40, 50]// [10, 20, 30, 60, 40, 50]// [10, 20, 30, 60, 40, 50]// [10, 20, 30, 50, 40, 60]// [10, 20, 30, 40, 50, 60]// [10, 20, 30, 40, 50, 60]
}
//快速排序
public static void quickSort(int[] arr, int start, int end) {
//递归结束的标记
if (start = stard) {
high--;
}
//右边数字比标准数小,使用右边的数替换左边的数
arr[low] = arr[high];
//如果左边数字比标准数小
while (low <h2>15.3 时间复杂度</h2>
O(nlogn)
O(n^2)
第16章 希尔排序
16.1 希尔排序概念


16.2 代码实现
import java.util.Arrays;public class ShellSort {
public static void main(String[] args) {
int[] arr = {8, 9, 1, 7, 2, 3, 5, 4, 6, 0};
shellSort(arr);// [3, 5, 1, 6, 0, 8, 9, 4, 7, 2]// [0, 2, 1, 4, 3, 5, 7, 6, 9, 8]// [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
}
//希尔排序
public static void shellSort(int[] arr) {
//遍历所有的步长
for (int gap = arr.length / 2; gap > 0; gap = gap / 2) {
//遍历所有的元素
for (int i = gap; i = 0; j -= gap) {
//如果当前元素大于加上步长后的那个元素
if (arr[j] > arr[j + gap]) {
int temp = arr[j];
arr[j] = arr[j + gap];
arr[j + gap] = temp;
}
}
}
//打印每次排序后的结果
System.out.println(Arrays.toString(arr));
}
}}
16.3 时间复杂度
O(n^2)
o(n^1.3)。第17章 堆排序
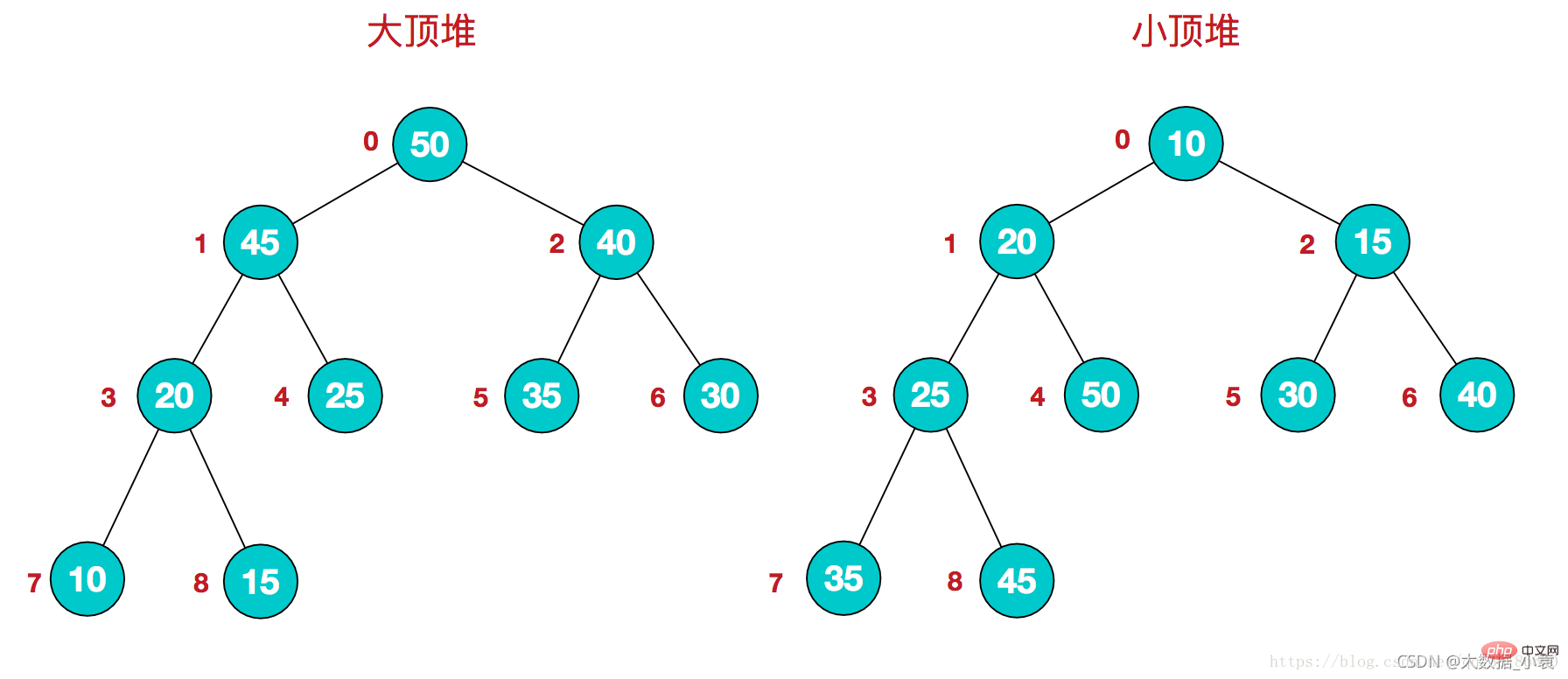
17.1 堆排序概述
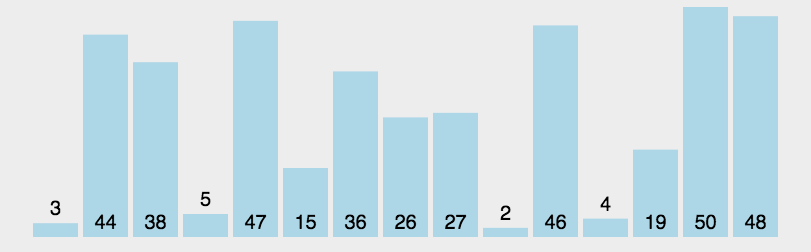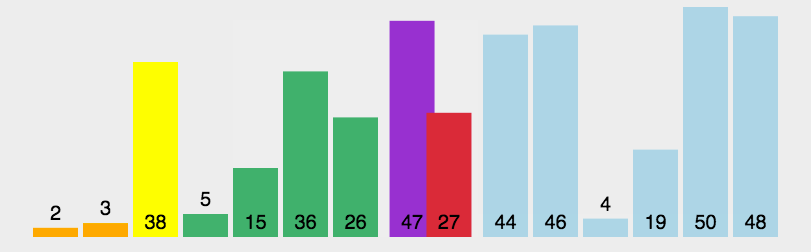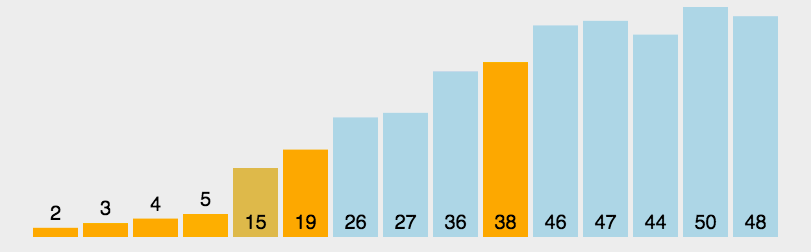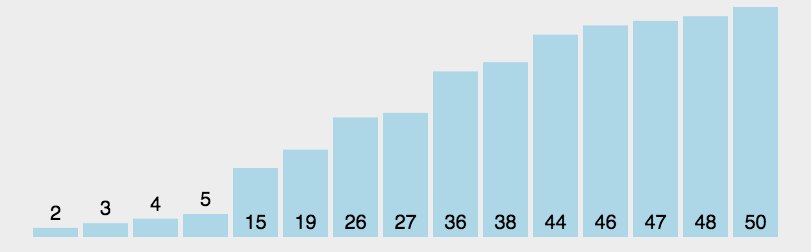
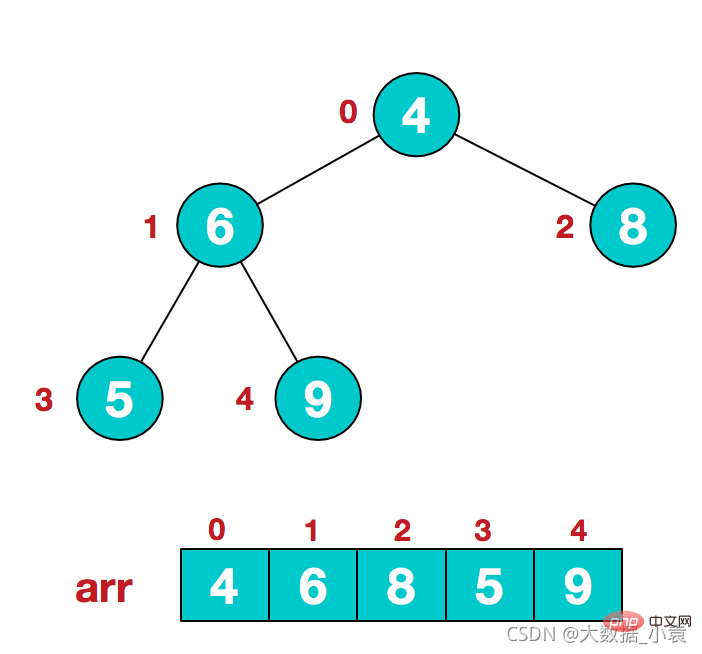
 同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子
同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子 该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
2)此时我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整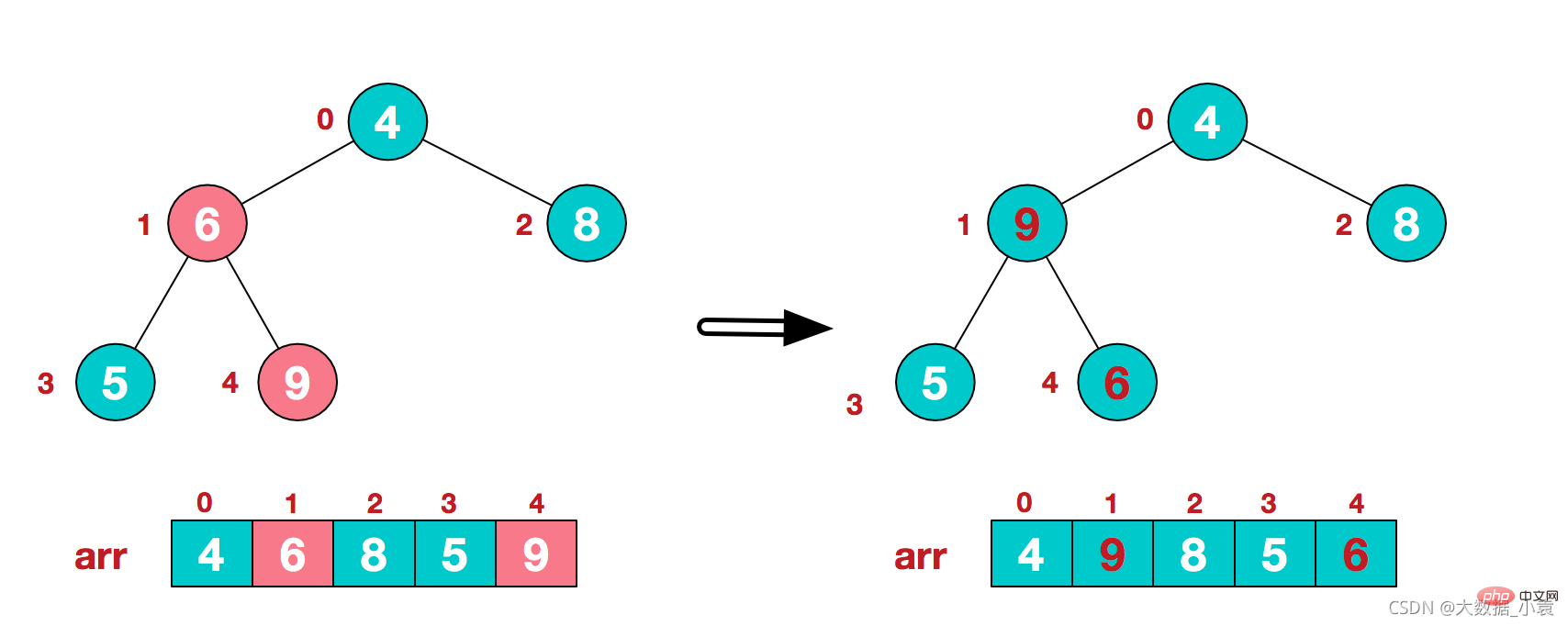
3)找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换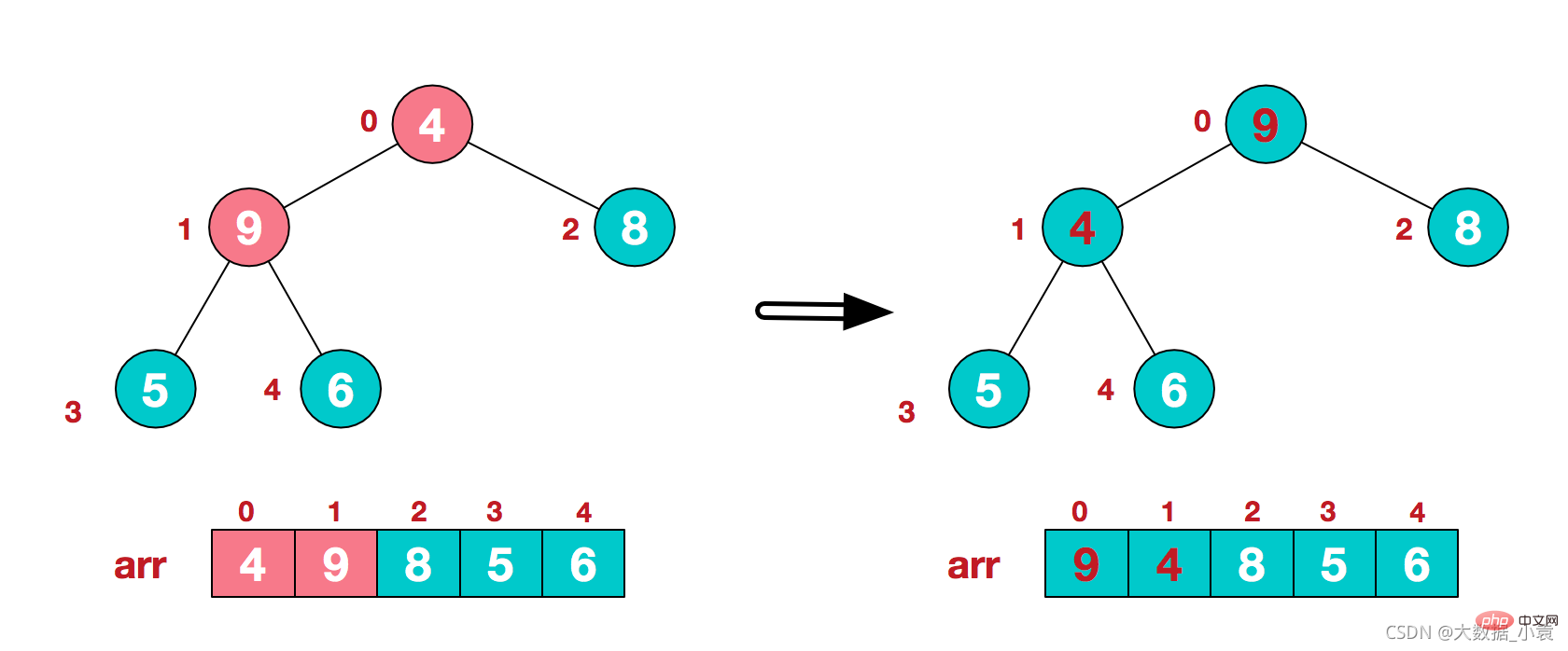 4)这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。
4)这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。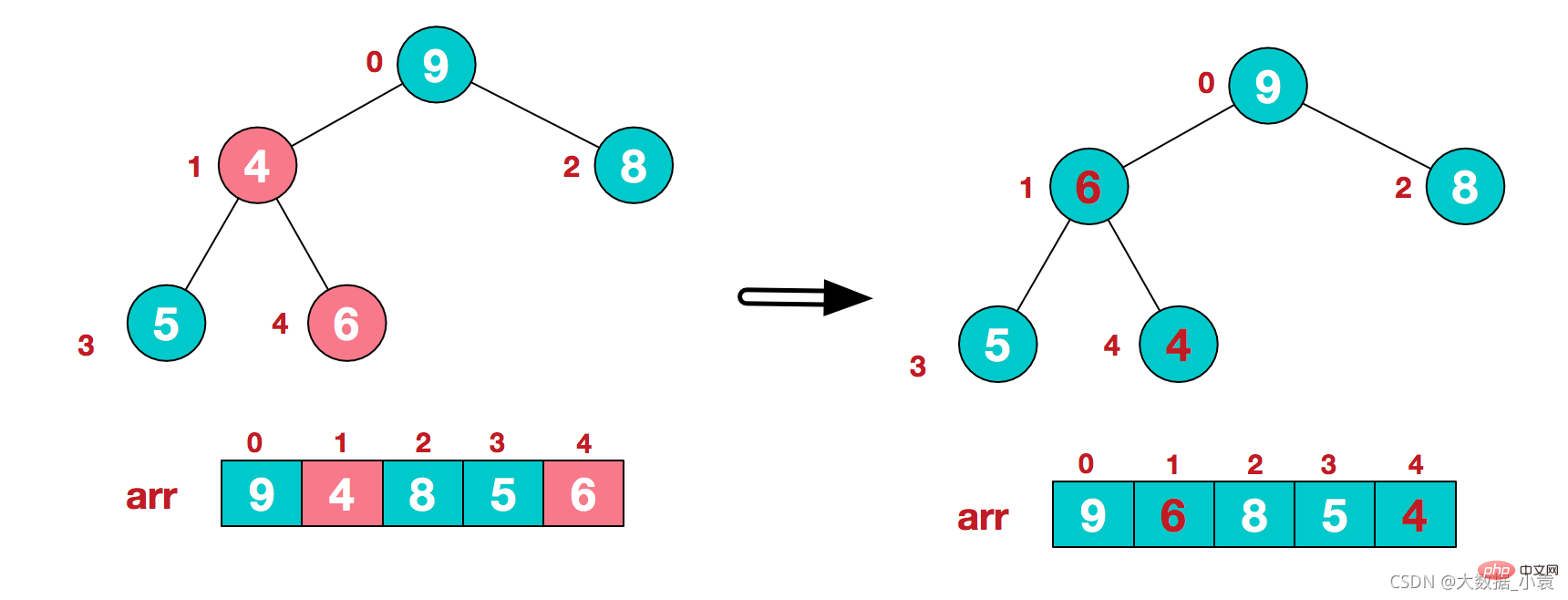 此时,我们就将一个无需序列构造成了一个大顶堆
此时,我们就将一个无需序列构造成了一个大顶堆
2)重新调整结构,使其继续构建大顶堆(9除外)
3)再将堆顶元素8与末尾元素5进行交换,得到第二大元素8.
步骤三 后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序

17.2 代码实现
import java.util.Arrays;public class HeapSort {
public static void main(String[] args) {
int[] arr = {4, 6, 8, 5, 9};
heapSort(arr);// [4, 6, 8, 5, 9]// [4, 9, 8, 5, 6]// [4, 9, 8, 5, 6]// [9, 6, 8, 5, 4]// [9, 6, 8, 5, 4]// [9, 6, 8, 5, 4]// [8, 6, 4, 5, 9]// [8, 6, 4, 5, 9]// [6, 5, 4, 8, 9]// [6, 5, 4, 8, 9]// [5, 4, 6, 8, 9]// [5, 4, 6, 8, 9]// [4, 5, 6, 8, 9]
}
//堆排序
public static void heapSort(int[] arr) {
//开始位置是最后一个非叶子节点(最后一个节点的父节点)
int start = (arr.length - 1) / 2;
//循环调整为大顶堆
for (int i = start; i >= 0; i--) {
maxHeap(arr, arr.length, i);
}
//先把数组中第0个和堆中最后一个交换位置
for (int i = arr.length - 1; i > 0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
//再把前面的处理为大顶堆
maxHeap(arr, i, 0);
}
}
//数组转大顶堆,size:调整多少(从最后一个向前减),index:调整哪一个(最后一个非叶子节点)
public static void maxHeap(int[] arr, int size, int index) {
//左子节点
int leftNode = 2 * index + 1;
//右子节点
int rightNode = 2 * index + 2;
//先设当前为最大节点
int max = index;
//和两个子节点分别对比,找出最大的节点
if (leftNode arr[max]) {
max = leftNode;
}
if (rightNode arr[max]) {
max = rightNode;
}
//交换位置
if (max != index) {
int temp = arr[index];
arr[index] = arr[max];
arr[max] = temp;
//交换位置后,可能会破坏之前排好的堆,所以之间排好的堆需要重新调整
maxHeap(arr, size, max);
}
//打印每次排序后的结果
System.out.println(Arrays.toString(arr));
}}
17.3 时间复杂度
o(nlogn)
o(nlogn)
O(nlogn)。第18章 计数排序
18.1 计数排序概念
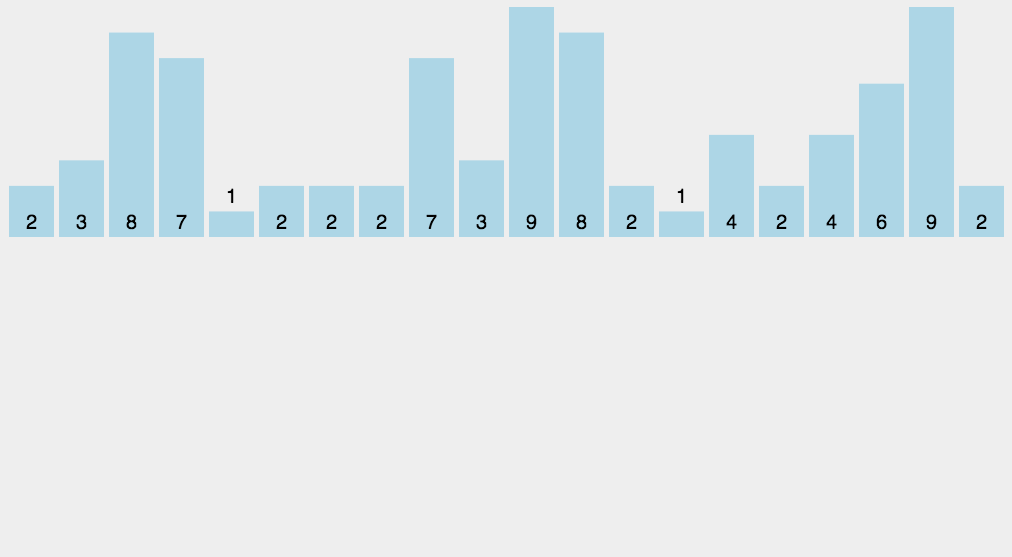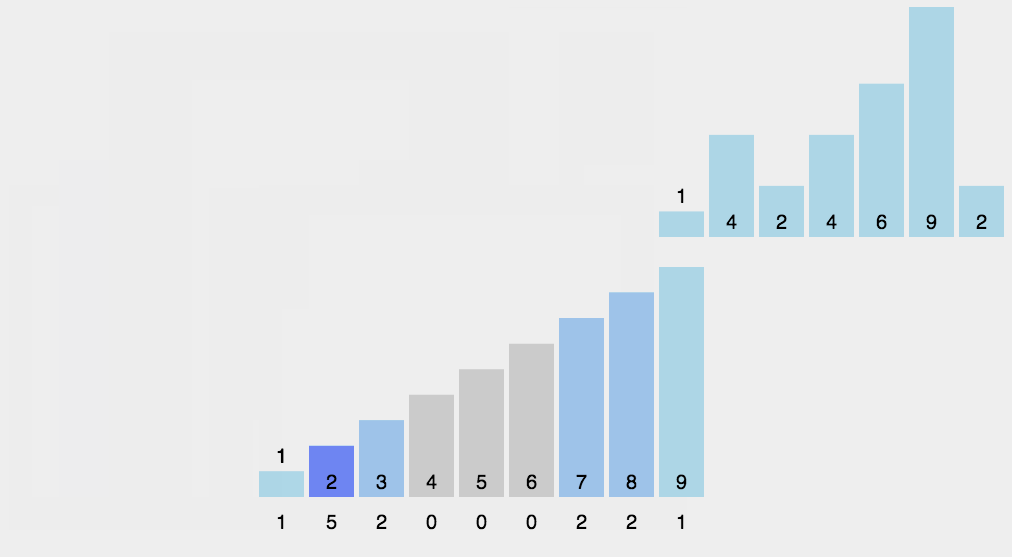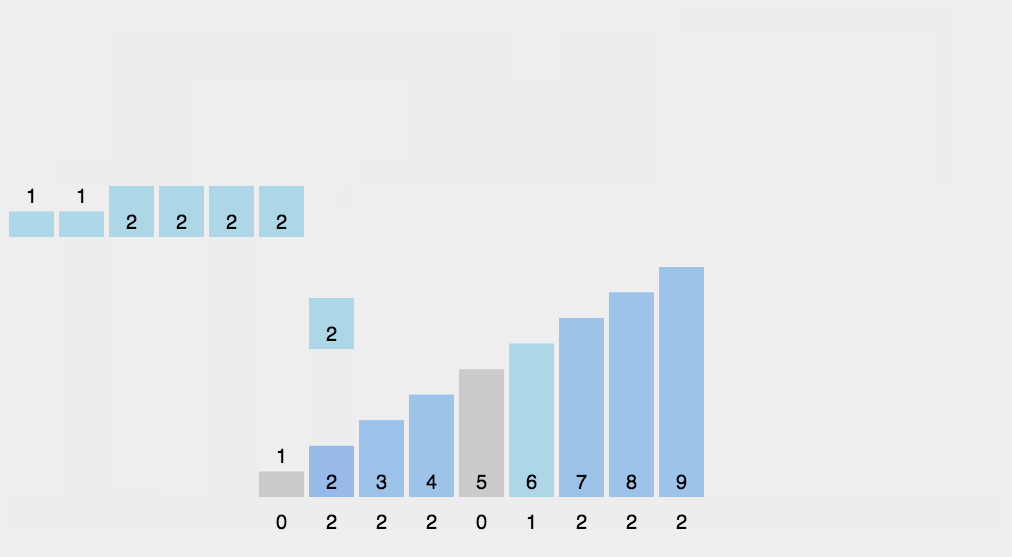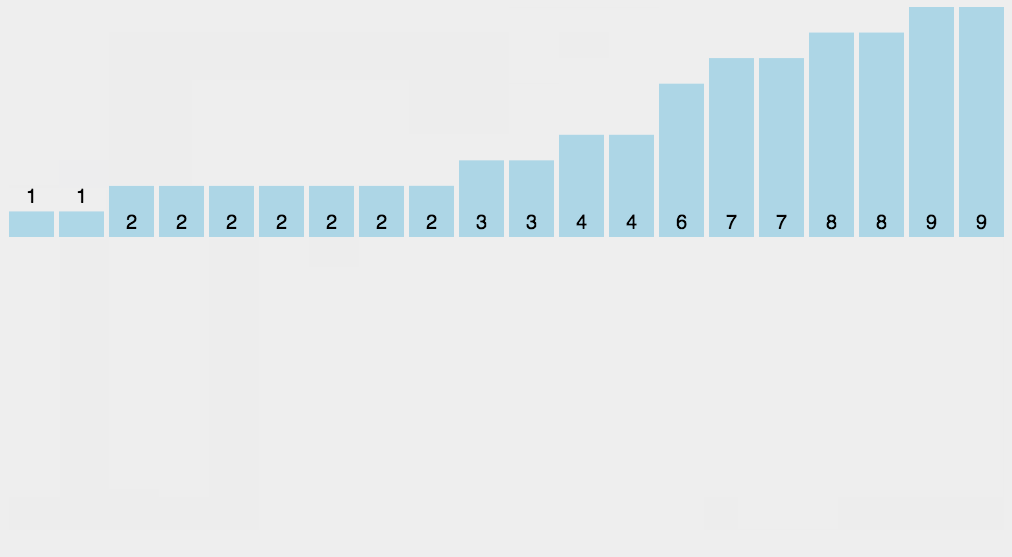
18.2 代码实现
import java.util.Arrays;public class CountingSort {
public static void main(String[] args) {
//测试
int[] arr = {1, 4, 6, 7, 5, 4, 3, 2, 1, 4, 5, 10, 9, 10, 3};
sortCount(arr);
System.out.println(Arrays.toString(arr));// [1, 1, 2, 3, 3, 4, 4, 4, 5, 5, 6, 7, 9, 10, 10]
}
//计数排序
public static void sortCount(int[] arr) {
//一:求取最大值和最小值,计算中间数组的长度:
int max = arr[0];
int min = arr[0];
int len = arr.length;
for (int i : arr) {
if (i > max) {
max = i;
}
if (i <h2>18.3 时间复杂度</h2>
o(n+k)
o(n+k)
O(n+k),空间复杂度也是O(n+k),其排序速度快于任何比较排序算法。当k不是很大并且序列比较集中时,计数排序是一个很有效的排序算法第19章 桶排序
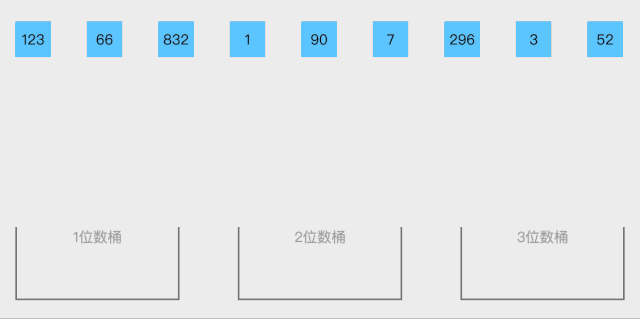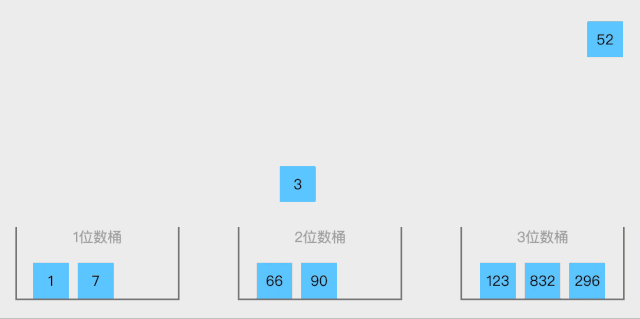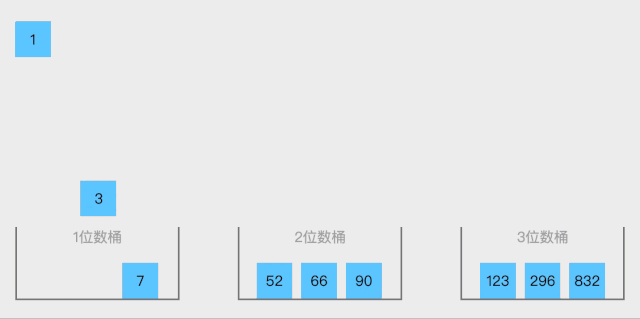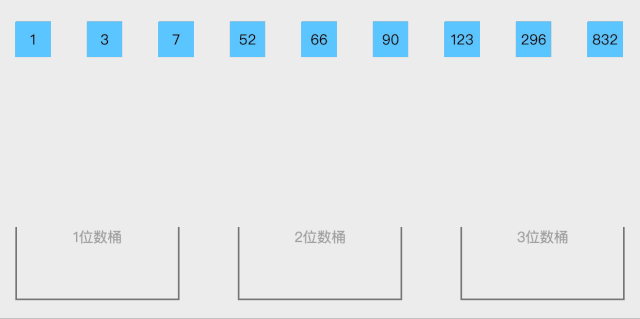
19.1 桶排序概念
o(n)。但桶排序并不是比较排序,他不受到O(n log n)下限的影响。

19.2 代码实现
package sort;import java.util.ArrayList;import java.util.Collections;public class BucketSort {
public static void main(String[] args) {
int[] arr = {29, 25, 3, 49, 9, 37, 21, 43};
bucketSort(arr);
//分桶后结果为:[[3, 9], [], [21, 25], [29], [37], [43, 49]]
}
public static void bucketSort(int[] arr) {
// 大的当小的,小的当大的
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
// 找出最小最大值
for (int i=0, len=arr.length; i<len>> bucketArr = new ArrayList(bucketNum);
// 这一步是不可缺少的,上面的初始化只初始化了一维列表。二维列表需额外初始化
for (int i=0; i<bucketnum>());
}
for (int i=0, len=arr.length; i<len><h2>19.3 时间复杂度</h2>
<ul>
<li>最优时间复杂度:o(n)</li>
<li>最坏时间复杂度:o(n^2)</li>
<li>稳定性:稳定</li>
</ul>
<p>对于桶排序来说,分配过程的时间是O(n);收集过程的时间为O(k) (采用链表来存储输入的待排序记录)。因此,桶排序的时间为<code>O(n+k)</code>。若桶个数m的数量级为O(n),则桶排序的时间是线性的,最优即O(n)。</p>
<p>前面说的几大排序算法 ,大部分时间复杂度都是O(n2),也有部分排序算法时间复杂度是O(nlogn)。而桶式排序却能实现O(n)的时间复杂度。但桶排序的缺点是:首先是空间复杂度比较高,需要的额外开销大。排序有两个数组的空间开销,一个存放待排序数组,一个就是所谓的桶,比如待排序值是从0到m-1,那就需要m个桶,这个桶数组就要至少m个空间。其次待排序的元素都要在一定的范围内等等。</p>
<h2>第20章 基数排序</h2>
<h2>20.1 基数排序概念</h2>
<p><strong>基数排序</strong>(Radix Sort)是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前</p>
<p><strong>排序步骤</strong>:</p>
<ul>
<li>取得数组中的最大数,并取得位数;</li>
<li>arr为原始数组,从最低位开始取每个位组成radix数组;</li>
<li>对radix进行计数排序(利用计数排序适用于小范围数的特点)</li>
</ul>
<p><strong>动图展示</strong>:</p>
<p><img src="https://img.php.cn/upload/article/000/000/067/e8617e003a5b8a2e40eb3c59220e97a6-113.gif" alt="Javaのデータ構造とアルゴリズムの詳細な図解説明"><br><strong>静图分析</strong>:</p>
<p><img src="https://img.php.cn/upload/article/000/000/067/e8617e003a5b8a2e40eb3c59220e97a6-114.png" alt="Javaのデータ構造とアルゴリズムの詳細な図解説明"></p>
<h2>20.2 代码实现</h2>
<pre class="brush:php;toolbar:false">import java.util.Arrays;public class RadixSort {
public static void main(String[] args) {
int[] arr = {4, 32, 457, 16, 28, 64};
radixSort(arr);// [32, 4, 64, 16, 457, 28]// [4, 16, 28, 32, 457, 64]// [4, 16, 28, 32, 64, 457]
}
//基数排序
public static void radixSort(int[] arr) {
// 定义临时二维数组表示十个桶
int[][] temp = new int[10][arr.length];
// 定义一个一维数组,用于记录在temp中相应的数组中存放数字的数量
int[] counts = new int[10];
//存数组中最大的数字
int max = Integer.MIN_VALUE;
for (int i = 0; i max) {
max = arr[i];
}
}
//计算最大数字是几位数(才能知道排序次数)
int maxLength = (max + "").length();
//根据最大长度的数决定比较的次数
for (int i = 0, n = 1; i <h2>20.3 时间复杂度</h2>
O(n^k)
O(n^k)
以上がJavaのデータ構造とアルゴリズムの詳細な図解説明の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

