ホームページ >バックエンド開発 >PHPチュートリアル >PHP データ構造におけるグラフ アプリケーションの最短パスは何ですか?
PHP データ構造におけるグラフ アプリケーションの最短パスは何ですか?
- 藏色散人転載
- 2021-07-03 14:46:302435ブラウズ
グラフの応用: 最短パス
前回の記事の最小スパニング ツリーについては、まだ学ぶ必要があると感じましたか?どれだけマスターできたかわかりませんが、プリムとクラスカルの原理は理解できましたか?面接で書けないなら、せめて大まかなイメージだけでも伝えてください もちろん大学院受験生であればアルゴリズム全体のコードを深く理解して覚えておく必要があります。
最短経路とは何ですか
今日私たちが学んでいるのは、グラフ アプリケーションにおけるもう 1 つの古典的な問題、つまり最短経路問題です。この問題は最小スパニングツリーとは異なり、すべてのノードを接続し、最小の重みを持つ経路を取ることが要件となります。最短パスとは、頂点から別の頂点までの重みが最小のパスを指します。このパスは最小スパニングツリーに含まれるとは限らないため、あまり関連性はありません。
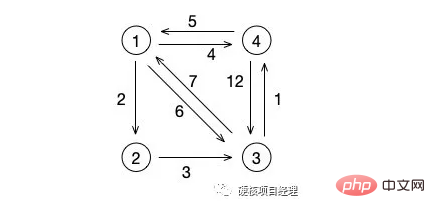
この図から、ノード 1 からノード 2 への最短パスは 2 であることがわかります。これは明らかです。では、ノード 1 からノード 3 まではどうなるでしょうか?重み 6 の直接の中間パスではなく、パス 1->2->3 (合計重み 5 のパス) です。
次に、ノード 3 を見てみましょう。ノード 1 への最短パスはパス 3->4->1 である必要があります。これは重み 6 のパスであり、中央の線には重みがありません。 7の。
はい、これが最短経路の概念です。通常、最短経路で一方向グラフの問題を解決しますが、実際にはどうなるでしょうか?最も典型的な地図関連アプリケーションは、実際には双方向グラフです。ただし、これは学習には影響しません。この例の図のノードは市内の駅とみなすことができます。ノード 1 とノード 3 を接続する鉄道路線であっても、必ずしも同時に行き来するとは限りません。たとえば、長沙から北京までの列車 Z2 の総走行時間は 14 時間 42 分ですが、列車 Z1 の戻り時間は 14 時間 10 分です。では、他の列車を選択できますか? たとえば、長沙から石家荘までわずか 8 時間、石家荘から北京までわずか 2 時間かかる列車があります。このようにすると、このルートを選択すると合計所要時間はわずか 10 時間になります。時間(もちろん、これは一例です。高速鉄道でない場合、人々は間違いなく始発駅の列車を選択します)。
マルチソース最短パス フロイド アルゴリズム
まず、マルチソース最短パス アルゴリズムについて説明します。では、マルチソースとは何でしょうか?
実際、このアルゴリズムはすべてのノードからすべてのノードへの最短パスを見つけることができます。そう、このアルゴリズムでは、どのノードからどのノードに行っても、その間の最短経路が一気に計算されます。魔法ですか?いや、いや、もっとすごいのは、すぐに「ああ、なんてことだ!」と叫んでしまうことでしょう、そのコア コードはわずか 5 行です。 !
function Floyd($graphArr){
$n = count($graphArr);
for($k = 1;$k<=$n;$k++){ // 设 k 为经过的结点
for($i = 1;$i<=$n;$i++){
for($j = 1;$j<=$n;$j++){
// 如果经过 k 结点 能使 i 到 j 的路径变短,那么将 i 到 j 之间的更新为通过 k 中转之后的结果
if($graphArr[$i][$j] > $graphArr[$i][$k] + $graphArr[$k][$j]){
$graphArr[$i][$j] = $graphArr[$i][$k] + $graphArr[$k][$j];
}
}
}
}
for($i = 1;$i<=$n;$i++){
for($j = 1;$j<=$n;$j++){
echo $graphArr[$i][$j], ' ';
}
echo PHP_EOL;
}
}
// 请输入结点数:4
// 请输入边数:8
// 请输入边,格式为 出 入 权:1 2 2
// 请输入边,格式为 出 入 权:1 3 6
// 请输入边,格式为 出 入 权:1 4 4
// 请输入边,格式为 出 入 权:2 3 3
// 请输入边,格式为 出 入 权:3 1 7
// 请输入边,格式为 出 入 权:3 4 1
// 请输入边,格式为 出 入 权:4 1 5
// 请输入边,格式为 出 入 权:4 3 12
// 0 2 5 4
// 9 0 3 4
// 6 8 0 1
// 5 7 10 0最初に結果を確認します。これは、コメントの最後にある行列の出力です。ノード 1 からノード 2、3、および 4 までの最短距離は 2、5、および 4 です。ノード 3 からノード 1、2、および 4 までの最短距離は 6、8、および 1 です。つまり、元のグラフの隣接行列が最短経路の行列となる。各行は、各ノードから他のノードまでの最短距離を表します。
わかりました、結果は問題ありません。それでは、コードは正確にどのようなもので書かれているのでしょうか?このkは何ですか?心配しないで、段階的に見てみましょう。
2 点間の距離が最短ではないと仮定すると、ジャンプの媒介となる別の点が必要になります。点 i から最初にこの点にジャンプし、次に点 j にジャンプします。このような経路は次のとおりです。 i から j への直接の点よりも近いので、この点を k 点として定義します。
しかし、どのノードに行けばよいのかわかりません。また、k が複数ある可能性があります。おそらく、i から j に行くのは、次のとおりです。このとき、ループの最初のレベルである k からトラバースを開始します。
ループの最初のレベルで、i と j の通常のトラバース ループを実行し、i を取得します。直接 j までの長さ、つまり [i][j]。このとき、一番外側の k の存在により、i が k から歩いた場合の k から j までの長さもわかります。これは、距離 [i][k] [k][i]
明らかに、[i][k] [k][i] の距離が [i][j] より短い場合は、[i][j] の値を [i][k] [k ][i に更新します。 ]
内部 i ループと j ループが完了した後、メディア ジャンプとしての最初のノードのトラバースも完了します。現在の行列の各ノード間の重みは、1 以降の最短パスを介して渡されます。ノードは媒体として使用されます
ただし、これは正確ではありません。おそらく、i、k1、k2、j を通過する可能性のあるパスが最短であるため、外側の k ループは引き続き通過し、2 番目のノードがは中間ノードとして使用されます。
すべてのノードが中間中間ノードを一度訪問するまでループが続き、最短パスのマトリックス グラフが得られます。つまり、ノード 4 とノード 3 を例に説明します。上記のテスト コード
# に結果が出力されます。 4 を i、ノード 3 を j として定義します。
初始化时,[i][j] 为 12 ,这个没什么问题,单向图的那条带箭头的边的权值就是 12 。
然后当 k 为 1 时,也就是我们经过结点 1 来看路径有没有变短,这时 [i][k] 是 5 ,[k][j] 是 6 ,OK,路径变成 11 了,把 [i][j] 的值改成 11 。
同时,在 i 为 4 ,j 为 2 的情况下,他们两个的最短路径也在这次 k=1 的循环中被赋值为 7 。最开始 4 到 2 是没有直接的边的,现在在结点 1 的连接下,他们有了路径,也就是 [4][2] = [4][1] + [1][2] = 7 。
当 k 为 2 时,[i][j] 为 11 ,这时 [i][k] 就是上面说过的 [4][2] 。也就是 7 ,而 [k][j] 则是 3 ,路径又缩小了,[i][k] + [k][j] = 10 ,[i][j] 现在又变成了 10 。
循环继续,但已经没有比这条路径更小的值了,所以最后 [4][2] 的最短路径就是 10 。
看着晕吗?拿出笔来在纸上或者本子上自己画画,每一步的 k 都去画一下当前的最短路径矩阵变成什么样了。这样画一次之后,马上就知道这个 Floyd 算法的核心奥秘所在了。
不得不说,前人的智慧真的很伟大吧,不过说是前人,其实 Floyd 大佬在 1962 年才发表了这个算法,但这个算法的核心思想却是数学中的动态规划的思想。所以说,算法和数学是没法分家的,各位大佬哪个不是数学界的一把手呢。
单源最短路径 Dijkstra 算法
说完了多源最短路径,我们再讲一个鼎鼎大名的单源最短路径的算法。虽说上面的多源很牛X,但是它的时间复杂度也就是时间效率也确实是太差了,没看错的话三个 N 次的循环嵌套就是 O(N3)。如果数据稍微多一点的话基本就可以从 Oh!My God! 变成 Oh!FxxK! 了。而且大多数情况下,我们的需求都会是固定的求从某一点到另一点的最短路径问题,也就是单源最短路径问题。这时,就可以使用这种效率稍微好一点的算法来快速地解决了。
// origin 表示源点,也就是我们要看哪个结点到其它结点的最短路径
function Dijkstra($graphArr, $origin)
{
$n = count($graphArr);
$dis = []; // 记录最小值
$book = []; // 记录结点是否访问过
// 初始化源点到每个点的权值
for ($i = 1; $i <= $n; $i++) {
$dis[$i] = $graphArr[$origin][$i]; // 源点到其它点的默认权值
$book[$i] = 0; // 所有结点都没访问过
}
$book[$origin] = 1; // 源点自身标记为已访问
// 核心算法
for ($i = 1; $i <= $n - 1; $i++) {
$min = INFINITY;
// 找到离目标结点最近的结点
for ($j = 1; $j <= $n; $j++) {
// 如果结点没有被访问过,并且当前结点的权值小于 min 值
if ($book[$j] == 0 && $dis[$j] < $min) {
$min = $dis[$j]; // min 修改为当前这个节点的路径值
$u = $j; // 变量 u 变为当前这个结点
}
// 遍历完所有结点,u 就是最近的那个顶点
}
$book[$u] = 1; // 标记 u 为已访问
for ($v = 1; $v <= $n; $v++) {
// 如果 [u][v] 顶点小于无穷
if ($graphArr[$u][$v] < INFINITY) {
// 如果当前 dis[v] 中的权值大于 dis[u]+g[u][v]
if ($dis[$v] > $dis[$u] + $graphArr[$u][$v]) {
// 将当前的 dis[v] 赋值为 dis[u]+g[u][v]
$dis[$v] = $dis[$u] + $graphArr[$u][$v];
}
}
}
// 最近的结点完成,继续下一个最近的结点
}
for ($i = 1; $i <= $n; $i++) {
echo $dis[$i], PHP_EOL;
}
}
// 请输入结点数:4
// 请输入边数:8
// 请输入边,格式为 出 入 权:1 2 2
// 请输入边,格式为 出 入 权:1 3 6
// 请输入边,格式为 出 入 权:1 4 4
// 请输入边,格式为 出 入 权:2 3 3
// 请输入边,格式为 出 入 权:3 1 7
// 请输入边,格式为 出 入 权:3 4 1
// 请输入边,格式为 出 入 权:4 1 5
// 请输入边,格式为 出 入 权:4 3 12
// 测试第四个结点到其它结点的最短路径
Dijkstra($graphArr, 4);
// 5
// 7
// 10
// 0代码一下增加了不少吧,不过仔细看一下核心的算法部分,这次只是两层循环的嵌套了,时间复杂度一下子就降到了 O(N2) ,这一下就比 Floyd 算法提升了很多。当然,它的场景也是有限的,那就是只能一个结点一个结点的计算。
好了,我们还是来看一下 Dijkstra 到底在干嘛吧。我们依然是使用上面那个简单的图,并且还是研究结点 4 到其它结点的算法执行情况。
首先,我们初始化结点 4 到其他所有结点的默认值,这时结点 4 到结点 2 是没有直接路径的,所以是无穷大,而到结点 1 是 5,到结点 3 是 12 。
然后将结点 4 标记为已访问,也就是 book[4] = 1
进入核心算法,从头开始遍历结点,这里是标记为 i 下标,因为这里是单源的最短路径,所以我们不需要再看自己到自己的最短路径了,只需要 n-1 次循环就可以了
开始 j 层的循环,先判断当前的结点是否已经被标记过,没有被标记过的话再看它的值是否是最小的,最后循环完成后获得一个从结点 4 出发的权值最小的路径,并将这条路径到达的结点下标记为 u ,标记 u 下标的这个结点为已访问结点
进入 v 循环,判断图中 u 到 v 的结点是否是无穷,如果不是的话再判断 u 到 v 的结点加上原来的 dis[u] 的权值是否小于 dis[v] 中记录的权值,如果比这个小的话,更新 dis[v] 为 u 到 v 的结点加上原来的 dis[u] 的权值
循环重复地进行比较完成算法
对于结点 4 来说,dis 经历了如下的变化:
首先,默认情况下 dis = [5, 9999999, 12, 0]
第一次循环后,结点1 完成查找,并在 v 的循环中发现了可以从结点1 到结点2 和结点3 而且比原来的值都要小 ,于是 dis = [5, 7, 11, 0]
第二次循环后,结点2 完成查找,这次循环发现从结点2 到结点3 的距离更短,于是 dis = [5, 7, 10, 0]
第三次循环后,结点3 完成查找,没有发现更短的路径,dis = [5, 7, 10, 0]
看明白了吗?不明白的话自己试试吧,不管是断点还是在中间输出一下 dis 和 book ,都能够帮助我们更好地理解这个算法的每一步是如何执行的。从代码中就可以看出来,这个 Dijkstra 算法的时间复杂度是 O(N2) ,这可比 Floyd 快了不少了吧。
总结
关于图的两种最典型的应用及算法就到这里结束了。当然,图的内容可远不止这些,比较典型的还是进度网络图等的算法,特别是做一些项目管理类的系统时会非常有用。当然,更高深的内容就要去研究《图论》了。这个可就远超我的水平了,希望有更多数学相关基础的同学能够继续深入研究。而我嘛,先去恶补下数学吧!!
测试代码: https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/5.图/source/5.5图的应用:最短路径.php
推荐:《PHP视频教程》
以上がPHP データ構造におけるグラフ アプリケーションの最短パスは何ですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

