検索

ホームページ  >  記事  >  バックエンド開発  >  PHP データ構造 - グラフの走査: 深さが優先、幅が優先

PHP データ構造 - グラフの走査: 深さが優先、幅が優先

藏色散人
藏色散人転載
2021-07-01 13:42:082586ブラウズ

グラフの走査: 深さ優先、幅優先

前の記事「PHP データ構造 - グラフのストレージ構造」では、グラフの関連するストレージ構造について学習しました。 、隣接行列および隣接リスト。これらはそれぞれ、シーケンシャル ストレージとチェーン ストレージの 2 つの最も一般的なタイプを表します。データ構造ができたので、当然次のステップはこれらのデータ構造の操作方法、つまりアルゴリズム部分を学習することです。グラフであってもツリーであっても、トラバースは非常に重要な部分です。今日はまず、最も基本的な 2 つのグラフトラバース方法を学びます。

ツリー走査はグラフ走査に進化しました

ツリーの研究では、事前順序、順序どおり、事後順序、およびレベル順序について説明したことを思い出してください。トラバーサル これらのトラバーサル形式は何ですか?実際、前順、中順、後順は一種のトラバース手法とみなすことができ、いずれもスタック構造を利用してトラバースし、最初に黒いパスに行き、その後、トラバースしていないパスに戻るのが特徴です。パス。レベル順走査は、キューを使用して階層ごとに走査し、最初に子ノードを走査し、次に各子ノードの次のレベルのノードを 1 つずつ走査するのが特徴です。

ツリー走査方法を確認した後、グラフ走査方法を学ぶのは非常に簡単になります。グラフ走査では、最も基本的な 2 つの走査形式がスタックとキューに基づいているためです。名前が少し異なるだけで、スタックベースのトラバーサル方法は深さ優先トラバーサルと呼ばれ、キューベースのトラバーサル方法は幅優先トラバーサルと呼ばれます。実際には、ツリーにおける初、中、最後の順走査と階層順走査に相当し、本質的には大きな違いはありません。

[推奨: PHP ビデオ チュートリアル ]

深さ優先トラバーサル

引き続きスタックからトラバースしますこの方法から始めます。これは、図の深さ優先トラバースの形式です。スタックの場合、他の子ノードがないことが判明するまで、新しいノードが継続的にスタックにプッシュされ、その後、元のパスが返されます。ノードに他のノードがあることが判明すると、子ノードはスタックにプッシュされます。スタック これはディープトラバーサルの考え方です。

ここで、訪問したノードを記録する必要があることに注意してください。特定のノードに接続されたパスを持つ複数のノードがある場合、このノードが 1 回だけ訪問されていることを確認してください。これがツリー構造との最大の違いです。ツリーは下まであり、水平方向のノード間の接続はなく、ノードには上位ノードが 1 つしかありません。グラフでは、任意のノードを他のノードに関連付けることができます。

隣接行列

まず、隣接行列の深さ優先トラバーサル アルゴリズムの実装を見てみましょう。今はわからなくても大丈夫なので、下にスクロールしてイラストを見て、一緒に読んでみてください。もちろん、より良い解決策は自分で実行することです。 

$visited = []; // 已访问结点
function DFS_AM($graphArr, $x)
{
    global $visited;
    echo "节点：{$x}", PHP_EOL;
    $visited[$x] = true; // 当前结点标记为已访问
     
    // y 就是邻接矩阵中的横行
    for ($y = 1; $y <= count($graphArr); $y++) {
        // 循环判断第 [x][y] 个数据是否为 1，也就是是否有边
        // 并且这个结点没有被访问过
        if ($graphArr[$x][$y] != 0 && !$visited[$y]) {
            // 进行栈递归，传递的参数是当前这个结点
            DFS_AM($graphArr, $y);
        }
    }
}
BuildGraph($graphArr); // 建立邻接矩阵图
echo &#39;请输入开始遍历的结点（1-结点数）：&#39;; 
fscanf(STDIN, "%d", $startNode); // 输入从第几个结点开始访问
DFS_AM($graphArr, $startNode); // 开始深度优先遍历

コード量はそれほど多くありません。前の記事で隣接行列を確立するコードを使用します。忘れた方は戻って見るか、リンクから直接ソースコードを読んでください。記事の下部にあります。

次にテストします: 

# php 5.3图的遍历：深度优先与广度优先.php
输入结点数：4
请输入边数：3
请输入边，格式为 出 入 权：1 2 1
请输入边，格式为 出 入 权：1 3 1
请输入边，格式为 出 入 权：3 4 1
请输入开始遍历的结点（1-结点数）：3
节点：3
节点：1
节点：2
节点：4

隣接リスト

もちろん、隣接リストを走査するという考え方は同じですが、途中でループアルゴリズムが使用されるのは、チェーン特性の方法です。 

$visited = [];  // 已访问结点
function DFS_AL($graph, $x){
    global $visited;
    $p = $graph->adjList[$x]; // 指定结点的第一个边结点
    echo "节点：{$x}", PHP_EOL; // 输出指定结点的信息
    $visited[$x] = true; // 设置该结点已被访问
    while($p != null){
        $y = $p->adjVex; // 获得边结点信息
        if(!$visited[$y]){ // 如果结点没有被访问过
            DFS_AL($graph, $y); // 进入这个边结点的深度遍历过程
        }
        $p = $p->nextArc; // 移动到下一个边结点
    }
}
$graph = BuildLinkGraph();
$graphBFS = $graph;
echo &#39;请输入开始遍历的结点（1-结点数）：&#39;;
fscanf(STDIN, "%d", $startNode); // 输入从第几个结点开始访问
DFS_AL($graph, $startNode);// 开始深度优先遍历

これも非常に簡単ですか? 次に簡単にテストしてみましょう: 

# php 5.3图的遍历：深度优先与广度优先.php
请输入 结点数 边数：
4 3
请输入边，格式为 出 入 权：1 2 1
请输入边，格式为 出 入 权：1 3 1
请输入边，格式为 出 入 权：3 4 1
请输入开始遍历的结点（1-结点数）：3
节点：3
节点：4
节点：1
节点：2

出力順序が隣接行列の順序と異なるのはなぜですか?前の記事で実装した隣接リストはヘッド補間を使用します。後の入力データはノード リンクの前に追加されます。最初の入力に 3 4 1 を入力すると、ノードは隣接行列と同じになります。トラバース結果は同じです。

深さ優先トラバーサルの図解

私は直接コードを見に来て、アルゴリズムについて長い間話しました。まだ混乱していますか?それは問題ではありません。図を直接見てみましょう。

PHP データ構造 - グラフの走査: 深さが優先、幅が優先

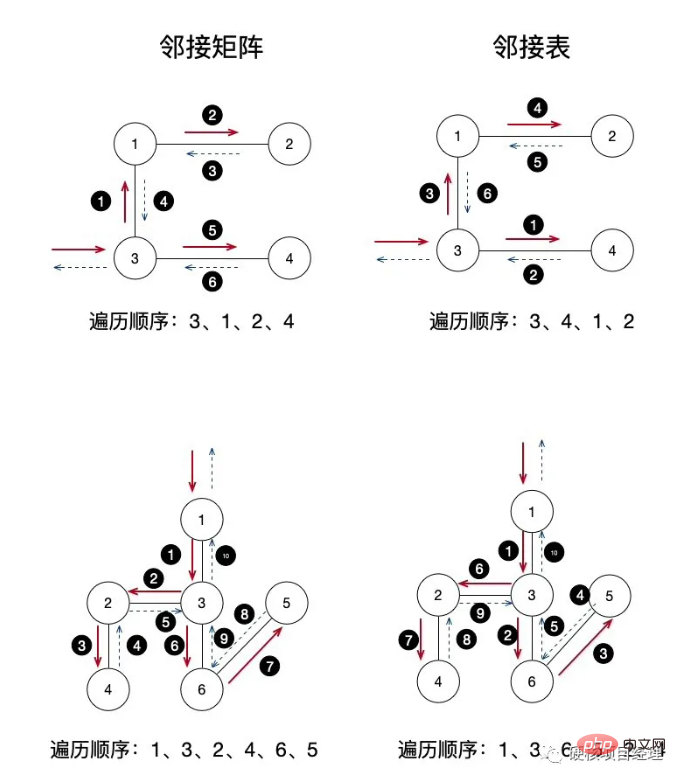
左側は隣接行列、右側は隣接リストです。私たちがテストしたグラフは 4 つのノードと 3 つのエッジを備えた比較的単純なグラフですが、次は 6 つのノードと 5 つのエッジを備えたより複雑なグラフです。自分でテストできます。各ステップの走査順序と実行順序については、小さな黒丸内の数字を確認してください。隣接行列の最初の図を使用して、アクセスの手順を簡単に説明します。

  • まず、ノード 3 から始まるアクセスを入力し、次に深度トラバーサルを開始して、結果ポイント 3

  • ループの最初のステップでは、ノード 3 にはノード 1 とのエッジがあるため、ノード 1 が再帰的に渡され、ノード 1 がスタックにプッシュされます

  • 出力ノード 1、現在の再帰のノード 1 はスタックの最上位にあります

  • 在 结点1 的循环中发现 结点1 和 结点 2 有边，于是递归传入 结点2 ，结点2 入栈

  • 输出 结点2，目前的递归中 结点2 在栈顶

  • 注意了，重点在这里，结点2 的循环中没有发现与其它未访问的结点有边存在了，于是递归开始返回，也就是开始出栈了，依次返回到 结点1 、结点3，没有任何输出，栈空了，递归回到最外层的函数了

  • 继续 结点3 的循环，发现与 结点4 有边，递归传入 结点4

  • 输出 结点4，目前的递归中 结点4 在栈顶

  • 结点4 的循环中没有发现其它未访问的结点及边了，递归返回，结点4 出栈

  • 结点3 循环完成，遍历结束

一步一步的很清晰吧，大家试着自己分析一下下面那个复杂一些图的深度遍历顺序，看看和我们程序输出的结果是不是一样的。在很多的考研或者数据结构考试中，经常会有选择题或应用题让你手动地来写出深度优先遍历的顺序哦！

广度优先遍历

接下来就是广度优先遍历了，其实说白了就是我们在学习树的遍历时候的层序遍历。前面我们说过，深度遍历是一条路走到黑，没路了退回来。而广度遍历则是一层一层的查看，直到找到出口。

邻接矩阵

使用邻接矩阵来进行广度优先遍历的操作，其实最核心的遍历方式和深度遍历没什么区别，都是对某一个结点进行边的查找，唯一不同的就是把递归栈换成了队列而已。

$visited = [];
function BFS_AM($graphArr, $x){
    global $visited;
    $queue = InitSqQueue(); // 初始化队列
    $graphCount = count($graphArr); // 获取矩阵结点数量
    $visited[$x] = true; // 结点标记为已访问
    EnSqQueue($queue, $x); // 结点入队
    while($x){ // 循环判断结点是否 fasle
        // 遍历所有结点是否与这个结点有边
        for ($y = 1; $y <= $graphCount; $y++) {
            // 如果有边并且未访问过
            if ($graphArr[$x][$y] != 0 && !$visited[$y]) {
                $visited[$y] = true; // 结点标记为已访问
                EnSqQueue($queue, $y); // 结点入队
            }
        }
        $x = DeSqQueue($queue); // 出队一个结点
        echo $x, PHP_EOL; // 输出结点
    }
}
echo &#39;请输入开始广度遍历的结点（1-结点数）：&#39;;
fscanf(STDIN, "%d", $startNode);
BFS_AM($graphArr, $startNode); // 开始广度遍历

代码中的注释也很清晰明了了，我们直接进行测试：

……
……
请输入开始广度遍历的结点（1-结点数）：3
3
1
4
2

邻接表

同样地，我们也提供邻接表的链式广度优先遍历的核心函数。

$visited = [];
function BFS_AL($graph, $x){
    global $visited;
    $visited[$x] = true; // 结点标记为已访问
    $queue = InitSqQueue();// 初始化队列
    EnSqQueue($queue, $x); // 结点入队
    
    // 如果一直有能出队的结点，就一直循环
    // 也就是说，如果队列空了，循环就结束
    while(($i = DeSqQueue($queue))!==false){
        echo $i, PHP_EOL; // 输出结点
        $p = $graph->adjList[$i]; // 结点的第一个边结点
        while($p != null){ // 如果不为空
            $y = $p->adjVex; // 边结点信息
            if(!$visited[$y]){ // 如果没有访问过
                $visited[$y] = true; // 标记结点为已访问
                EnSqQueue($queue, $y); // 入队结点
            }
            $p = $p->nextArc; // 结点指针指向下一个
        }
    }
}
echo &#39;请输入开始遍历的结点（1-结点数）：&#39;;
fscanf(STDIN, "%d", $startNode);
BFS_AL($graph, $startNode); // 开始广度遍历

核心的循环中的操作其实也和深度遍历没什么太大的区别，同样是换成了队列这种存储形式而已。

……
……
请输入开始广度遍历的结点（1-结点数）：3
3
4
1
2

广度优先遍历图示

好吧，上面又罗列完了算法，接下来就是图示的时间了，相信还是一看图大家就马上能明白广度优先遍历的具体步骤了。

PHP データ構造 - グラフの走査: 深さが優先、幅が優先

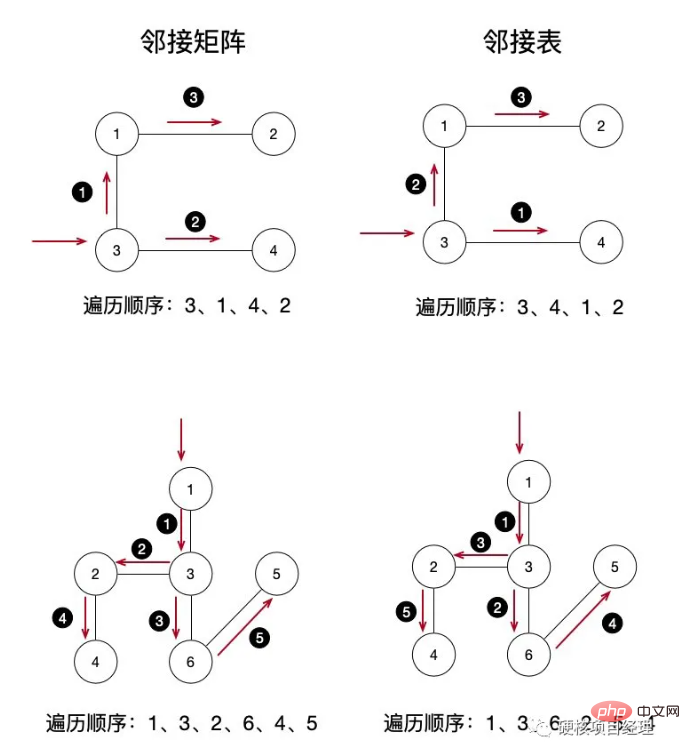
和上面的图一样，同样还是左边是邻接矩阵，右边是邻接表。在这里，我们依然还是直接分步骤来看一下左边最上面图的遍历操作顺序：

  • 输入 结点3 开始广度遍历，结点标记为已访问，这时 结点3 入队

  • 使用 while 循环判断 结点x 是否为 null ，如果不为 null 进入循环体

  • 遍历所有结点是否与这个结点有边，如果有边，并且这个结点没有被访问过，标记已访问，加入队列

  • 出队一个元素，并赋值给 x

  • 输出 x 结点的信息

广度优先遍历没有栈的回溯，就是一条线性的队列走完就完了，所以图示会非常清晰。单独一个结点我们会将和它相关的所有结点入队，然后出队最顶上的结点，这样就能够像树的层序遍历一样按照一层一层的顺序来遍历整个图。同样地，拿起纸笔，找复杂一点的图，试试能不能手写出类似于广度优先遍历顺序的题目吧！

总结

大家学完了之后是不是发现今天介绍的深度优先和广度优先两种遍历方式真的和树的遍历方式没什么太大的区别。最大的不同就是我们要标记已访问过的结点而已。不管怎么说，使用栈和队列来对树或图进行遍历是所有树和图的操作算法中最最基础的部分，也是考试和面试中最常见的问题，大家一定要深入理解掌握哦！

测试代码：
https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/5.图/source/5.3图的遍历：深度优先与广度优先.php

以上がPHP データ構造 - グラフの走査: 深さが優先、幅が優先の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

声明：
この記事は硬核项目经理で複製されています。侵害がある場合は、admin@php.cn までご連絡ください。
前の記事：PHP におけるオブザーバー パターンの詳細な分析次の記事：PHP におけるオブザーバー パターンの詳細な分析

関連記事

続きを見る