バイナリ ツリーには 5 つの基本的な形式があります: 1. 空のバイナリ ツリー、2. ルート ノードが 1 つだけあるバイナリ ツリー、3. 左のサブツリーのみ、4. 右のサブツリーのみ、5. 完全なバイナリ ツリー。

バイナリ ツリーには 5 つの基本的な形式があります
1) 空のバイナリ ツリー: 空のツリー;
2) ルート ノードが 1 つだけあるバイナリ ツリー: ルート、つまり単一ノードだけを持つツリー;
3) 左サブツリーのみ: ルートと左サブツリー;
4) 右サブツリーのみ: ルートがあり、右サブツリーがあります;
5) 完全なバイナリ ツリー: ルートがあり、左サブツリーと右サブツリーがあります。
特別なタイプ:
1. 完全なバイナリ ツリー: バイナリ ツリーに次数 0 のノードと次数 2 のノードのみがあり、次数が 0 の場合が同じレベルにある場合、バイナリ ツリーは完全なバイナリ ツリーです。
2. 完全なバイナリ ツリー: 各ノードが深さ k および n のノードを持つ完全なバイナリ ツリーに関連している場合に限り、深さ k および n のノードを持つバイナリ ツリー。 n 個のノードが 1 対 1 に対応するとき、それは完全二分木と呼ばれます。
完全な二分木の特徴は、葉ノードが最大の順序を持つ 2 つのレベルにのみ表示され、ノードの左の枝の下にある子孫の最大順序が子孫の最大順序に等しいことです。右の分岐の下にある、または 1 より大きい。
バイナリ ツリーは、重要なタイプのツリー構造です。多くの現実的な問題から抽象化されたデータ構造は二分木の形式であることが多く、通常の木であっても二分木への変換は容易であり、また二分木の記憶構造やアルゴリズムは比較的単純であるため、二分木は特に重要である。二分木の特徴は、各ノードが最大 2 つの部分木しか持てず、左右の部分木に分割できることです。
バイナリ ツリーは、n 個の有限要素のセットです。このセットは空であるか、ルートと呼ばれる 1 つの要素と、それぞれ左サブツリーおよび右サブツリーと呼ばれる 2 つの互いに素な要素で構成されています。二分木であり、順序付き木です。集合が空の場合、二分木は空二分木と呼ばれます。バイナリ ツリーでは、要素はノードとも呼ばれます。
関連知識の詳細については、PHP 中国語 Web サイトをご覧ください。 !
以上が二分木には基本的な形式がいくつありますか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 在C语言中打印二叉树的左视图Sep 03, 2023 pm 01:25 PM
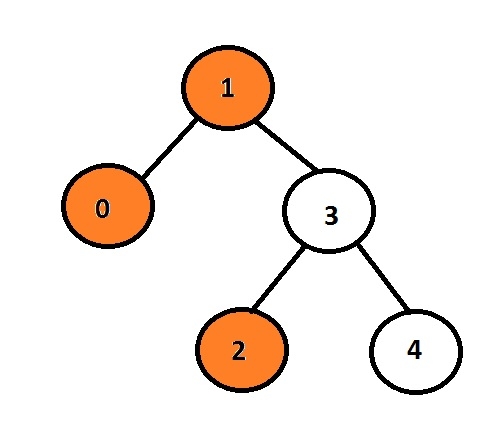
在C语言中打印二叉树的左视图Sep 03, 2023 pm 01:25 PM任务是打印给定二叉树的左节点。首先,用户将插入数据,从而生成二叉树,然后打印所形成的树的左视图。每个节点最多可以有2个子节点,因此这里程序必须仅遍历与节点关联的左指针如果左指针不为空,则意味着它将有一些与之关联的数据或指针,否则它将是要打印并显示为输出的左子级。示例Input:10324Output:102这里,橙色节点代表二叉树的左视图。在给定的图中,数据为1的节点是根节点,因此它将被打印,而不是转到左子节点,它将打印0,然后它将转到3并打印其左子节点,即2。我们可以使用递归方法来存储节点的级
 Java中的二叉树结构详解Jun 16, 2023 am 08:58 AM
Java中的二叉树结构详解Jun 16, 2023 am 08:58 AM二叉树是计算机科学中常见的数据结构,也是Java编程中常用的一种数据结构。本文将详细介绍Java中的二叉树结构。一、什么是二叉树?在计算机科学中,二叉树是一种树形结构,每个节点最多有两个子节点。其中,左侧子节点比父节点小,右侧子节点则比父节点大。在Java编程中,常用二叉树表示排序,搜索以及提高对数据的查询效率。二、Java中的二叉树实现在Java中,二叉树
 在C语言中,将二叉树的右视图打印出来Sep 16, 2023 pm 11:13 PM
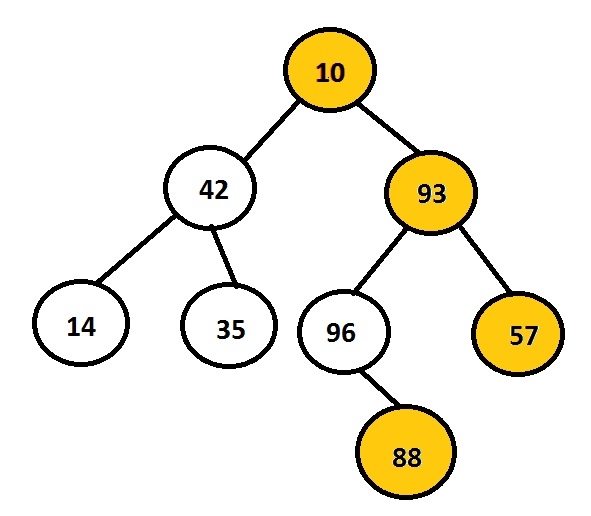
在C语言中,将二叉树的右视图打印出来Sep 16, 2023 pm 11:13 PM任务是打印给定二叉树的右节点。首先用户将插入数据以创建二叉树,然后打印所形成的树的右视图。上图展示了使用节点10、42、93、14、35、96、57和88创建的二叉树,其中选择并显示在树的右侧的节点。例如,10、93、57和88是二叉树的最右节点。示例Input:1042931435965788Output:10935788每个节点都有两个指针,即左指针和右指针。根据这个问题,程序只需遍历右节点。因此,不需要考虑节点的左子节点。右视图存储了所有那些是其所在层级的最后一个节点的节点。因此,我们可以
 如何使用Python实现二叉树的遍历Jun 09, 2023 pm 09:12 PM
如何使用Python实现二叉树的遍历Jun 09, 2023 pm 09:12 PM作为一种常用的数据结构,二叉树经常被用来存储数据、搜索和排序。遍历二叉树是非常常见的操作之一。Python作为一种简单易用的编程语言,有许多方法可以实现二叉树的遍历。本文将介绍如何使用Python实现二叉树的前序、中序和后序遍历。二叉树的基础在学习二叉树的遍历之前,我们需要了解二叉树的基本概念。二叉树由节点组成,每个节点都有一个值和两个子节点(左子节点和右子
 二叉树中等腰三角形的数量Sep 05, 2023 am 09:41 AM
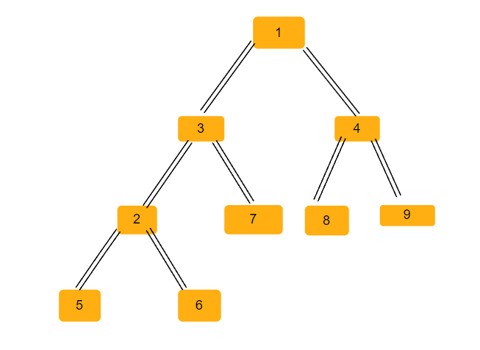
二叉树中等腰三角形的数量Sep 05, 2023 am 09:41 AM二叉树是一种数据结构,其中每个节点最多可以有两个子节点。这些孩子分别称为左孩子和右孩子。假设我们得到了一个父数组表示,您必须使用它来创建一棵二叉树。二叉树可能有几个等腰三角形。我们必须找到该二叉树中可能的等腰三角形的总数。在本文中,我们将探讨几种在C++中解决这个问题的技术。理解问题给你一个父数组。您必须以二叉树的形式表示它,以便数组索引形成树节点的值,而数组中的值给出该特定索引的父节点。请注意,-1始终是根父节点。下面给出的是一个数组及其二叉树表示。Parentarray=[0,-1,3,1,
 Java二叉树实现及具体应用案例详解Jun 15, 2023 pm 11:03 PM
Java二叉树实现及具体应用案例详解Jun 15, 2023 pm 11:03 PMJava二叉树实现及具体应用案例详解二叉树是一种经常在计算机科学中使用的数据结构,可以进行非常高效的查找和排序操作。在本文中,我们将讨论Java中如何实现二叉树及其一些具体应用案例。二叉树的定义二叉树是一种非常重要的数据结构,由根节点(树顶节点)和若干个左子树和右子树组成。每个节点最多有两个子节点,左边的子节点称为左子树,右边的子节点称为右子树。如果节点没有
 PHP实现二叉树的方式与应用Jun 18, 2023 pm 06:28 PM
PHP实现二叉树的方式与应用Jun 18, 2023 pm 06:28 PM在计算机科学中,二叉树是一种重要的数据结构。它由节点和指向它们的边组成,每个节点最多连接两个子节点。二叉树的应用广泛,例如搜索算法、编译器、数据库、内存管理等领域。许多编程语言都支持二叉树数据结构的实现,其中PHP是其中之一。本文将介绍PHP实现二叉树的方式以及其应用。二叉树的定义二叉树是一种数据结构,它由节点和指向它们的边组成。每个节点最多连接两个子节点,
 PHP中的二叉树算法及常见问题解答Jun 09, 2023 am 09:33 AM
PHP中的二叉树算法及常见问题解答Jun 09, 2023 am 09:33 AM随着Web开发的不断发展,PHP作为一种广泛使用的服务器脚本语言,其算法和数据结构也越来越重要。在这些算法和数据结构中,二叉树算法是一个非常重要的概念。本文将介绍PHP中的二叉树算法及其应用,以及常见问题的解答。什么是二叉树?二叉树是一种树形结构,其中每个节点最多有两个子节点,分别为左子节点和右子节点。如果节点没有子节点,则称其为叶子节点。二叉树通常用于搜索

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

SublimeText3 英語版
推奨: Win バージョン、コードプロンプトをサポート!

SublimeText3 中国語版
中国語版、とても使いやすい

WebStorm Mac版
便利なJavaScript開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

SublimeText3 Linux 新バージョン
SublimeText3 Linux 最新バージョン

ホットトピック
 7448
7448 15
15 1374
1374 52
52


